再谈矩阵快速幂
再谈矩阵快速幂
矩阵乘法
对于一个大小为 \(a\times m\) 的矩阵 \(A\) 和一个大小为 \(m\times b\) 的矩阵 \(B\),相乘可得一个大小为 \(a\times b\) 的矩阵 \(C\),如下。
那么对于矩阵 \(C\) 的每一个元素 \(C_{i,j}\),有 \(C_{i,j}=\sum_{k=1}^{m}A_{i,k}\times B_{k,j}\)。
形象化的,画个图。
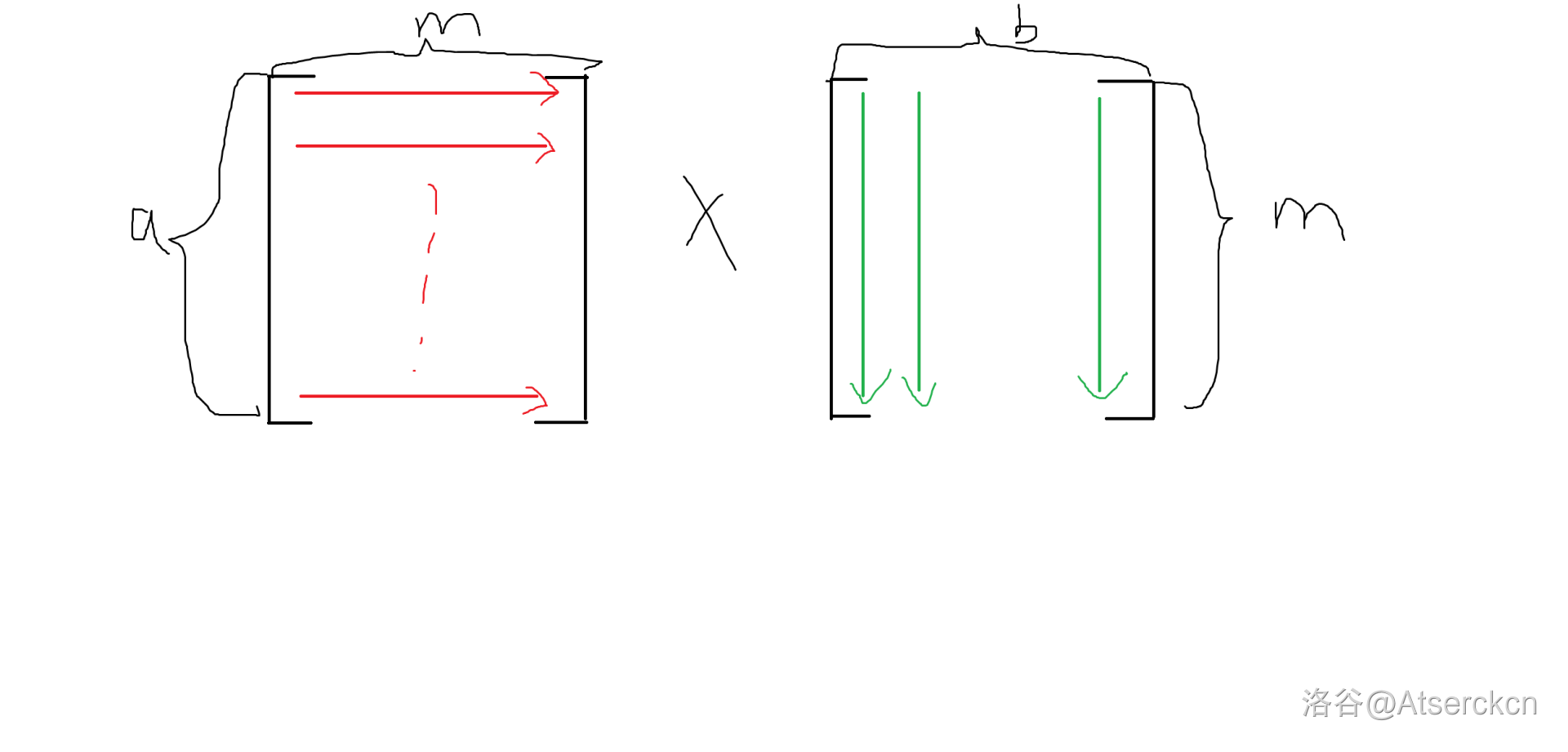
上图中 \(A\) 矩阵共 \(a\) 行,第 \(i\) 行的 \(m\) 个数都与 \(B\) 矩阵的第 \(j\) 列相匹配,得到 \(C_{i,j}\)。
代码实现:
Matrix operator * (const Matrix &a,const Matrix &b)
{
Matrix ans(0);
for(int i=1;i<=m;++i)
for(int j=1;j<=m;++j)
for(int k=1;k<=m;++k)
ans.v[i][j]=(ans.v[i][j]%Mod+a.v[i][k]%Mod*b.v[k][j]%Mod)%Mod;
return ans;
}
对于矩阵乘法满足结合律的证明
即对于任意三个矩阵 \(A,B,C\),\((A\times B)\times C=A\times(B\times C)\)。
看看就行,知道满足结合律即可。自己证一遍没必要,看得头痛。
矩阵乘法的单位元
单位元的定义:对于一种运算 \(op\),若 \(\forall a\ op\ b=a\),则称 \(b\) 是运算 \(op\) 的单位元。
比如说加减法的单位元是 \(0\),乘除法的单位元是 \(1\)。
那么矩阵乘法的单位元呢?
可以自己验算一下,对于一个 \(1\times n\) 的矩阵,它的单位元 \(f\) 应为一个 \(n\times n\) 的矩阵,满足:
即仅有对角线元素是 \(1\),其余为 \(0\)。
那么对于一个矩阵 \(a\),\(a^0=f\)。
快速幂
基础算法,可以用 \(\log\) 的时间复杂度解决出 \(a^n\)。
那么对于矩阵也适用。合称即为矩阵快速幂。
搭配上矩阵乘法,就可以通过洛谷P3390 【模板】矩阵快速幂。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ljl;
const int N=105,Mod=1e9+7;
ljl k;int n;
struct M{
int v[N][N];
M(int x)
{
memset(v,0,sizeof(v));
for(int i=1;i<N;++i)
v[i][i]=x;
}
}a(0),r(1);
M operator * (const M &a,const M &b)
{
M r(0);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
for(int k=1;k<=n;++k)
r.v[i][j]=(r.v[i][j]+1ll*a.v[i][k]*b.v[k][j])%Mod;
return r;
}
M qpow(M a,ljl k)
{
M ans(1);
while(k)
{
if(k&1)ans=ans*a;
a=a*a;
k>>=1;
}
return ans;
}
int main(){
ios::sync_with_stdio(0);
cin>>n>>k;
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
cin>>a.v[i][j];
r=qpow(a,k);
for(int i=1;i<=n;++i)
{
for(int j=1;j<=n;++j)
cout<<r.v[i][j]<<' ';
cout<<'\n';
}
return 0;
}
矩阵快速幂的应用场景及一般使用步骤
在解决问题中,矩阵常用来存储状态和附带属性。
适用于一些满足以下条件的递推:
- 暴力 \(O(n)\) 递推时间不够
- 可以滚动数组(如背包、Floyd)
对于满足上述条件的场景,一般应用矩阵快速幂解决的步骤:
- 构造出基础矩阵,一般为 \(1\times n\),存储基本状态,设为 \(a\)。
- 构造转移矩阵 \(fac\),满足当 \(a\) 存储上一个状态时,\(fac\times a\) 组成的矩阵存储当前状态。
构造好后,就可以联系上快速幂。
在一般情况下,状态矩阵大小为 \(1\times a\),转移矩阵大小为 \(a\times a\)。
假设我们要进行 \(k\) 轮递推,那么第 \(i\) 轮递推就是由第 \(i-1\) 轮的答案乘上转移矩阵得到。
比如说,从 \(a\) 转移到 \(b\),状态矩阵为 \(fac\)。
一般来说,矩阵变化一次仅多算出一个元素。
形象的,是这样:
其中,答案为 \(ans\),共有 \(k\) 个 \(fac\)。即:
那么 \(fac^k\) 就可以运用快速幂进行快速求解。求解时间是 \(\log\) 级别。
对于构造转移矩阵的一些技巧
此处状态矩阵大小为 \(1\times a\),转移矩阵大小为 \(a\times a\)。
上文提到,一般来说,矩阵变化一次仅多算出一个元素。
对于一次转移:
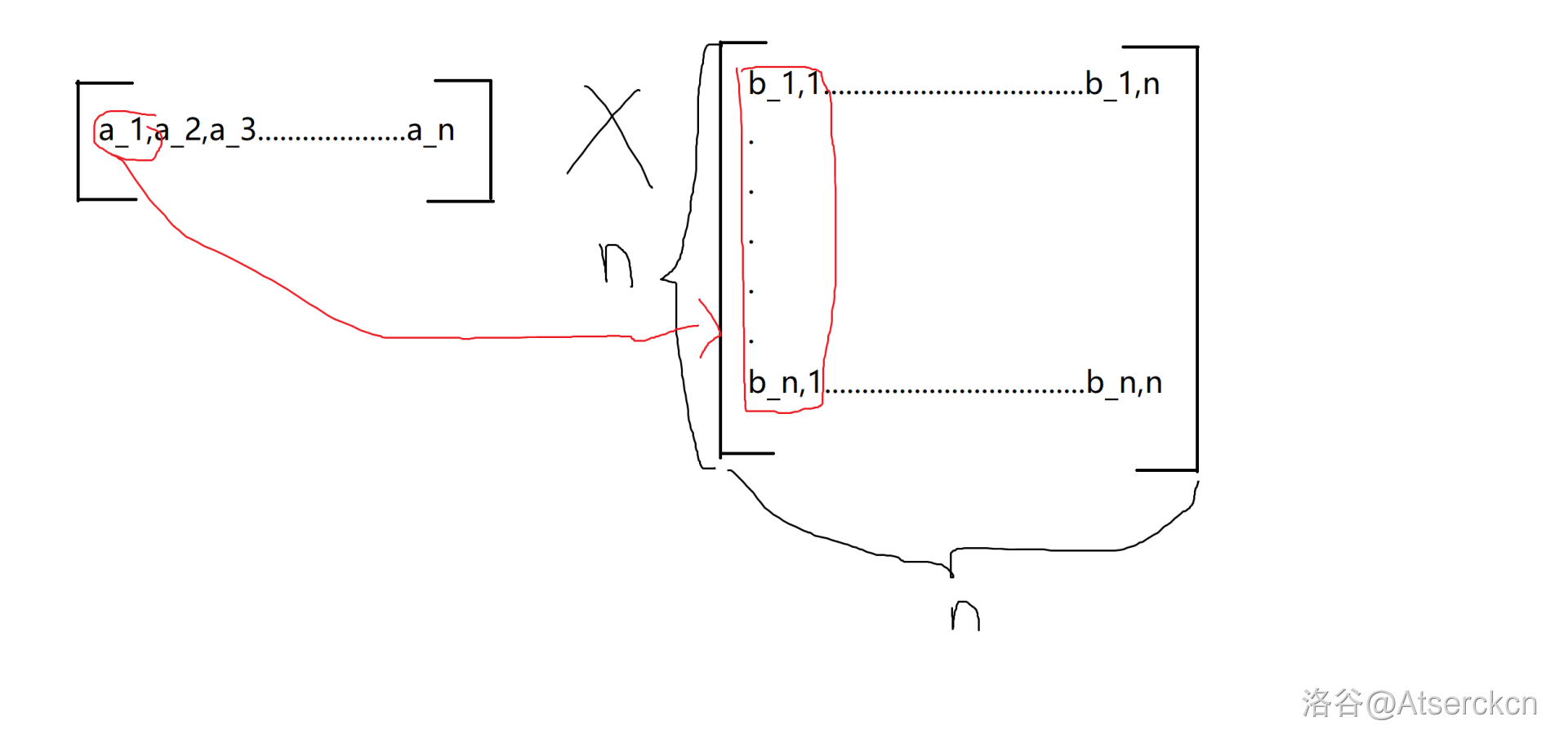
即对于每一个 \(a_i\),\(a_i=\sum_{j=1}^n a_j\times b_{j,i}\)。
那么 \(b\) 就可以当作是对于每个 \(a_i\) 的系数。
即转移可以表示为 \(a_1\times b_1+a_2\times b_2+\cdots a_n\times b_n\) 的形式。
那么我们就可以分析每一个 \(a_i\),为它“量身定做”一个转移的系数数列 \(b\),\(b\) 就构成了转移矩阵的第 \(i\) 列。
一些例题
例1.斐波那契数列
大家都知道,斐波那契数列是满足如下性质的一个数列:
求 \(F_n \bmod 10^9 + 7\) 的值。(\(n<2^{63}\))
那么对于基础的递推,时间 \(O(n)\),显然会炸。
考虑矩阵快速幂。
设状态矩阵 \(a\) 为 \([f_{i},f_i+1]\),显然初始时 \(a=[f_1,f_2]\)。
那么我们每次转移就是把 \([f_{i-1},f_i]\rightarrow [f_i,f_{i+1}]\),有且多算了仅一个元素。
那么我们一起构建下转移矩阵。设 \(-1\) 为还未构建。
先考虑转移后的 \(f_i\)。显然 \(f_i=f_{i-1}\times 0+f_i\times 1\)。所以目前状态矩阵为:
再看 \(f_i+1\)。此时就跟递推差不多,\(f_{i+1}=f_i\times 1+f_{i-1}\times 1\),所以我们就得到了完好的转移矩阵:
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ljl;
const ljl Mod=1e9+7;
ljl n;
struct M{
ljl v[5][5];
M(ljl x)
{
for(ljl i=1;i<=2;++i)
for(ljl j=1;j<=2;++j)
v[i][j]=(i==j?x:0);
}
}base(1),a(0);
M operator * (const M &a,const M &b)
{
M r(0);
for(ljl i=1;i<=2;++i)
for(ljl j=1;j<=2;++j)
for(ljl k=1;k<=2;++k)
r.v[i][j]=(r.v[i][j]+a.v[i][k]*b.v[k][j])%Mod;
return r;
}
M qpow(M a,ljl k)
{
M res(1);
while(k>0)
{
if(k&1)
res=res*a;
a=a*a;
k=k>>1;
}
return res;
}
int main(){
ios::sync_with_stdio(0);
cin>>n;
if(n<=2)
{
cout<<"1\n";return 0;
}
/*
0 1
1 1
*/
a.v[1][1]=0;a.v[1][2]=1;
a.v[2][1]=1;a.v[2][2]=1;
// for(int i=1;i<=2;++i)
// {
// for(int j=1;j<=2;++j)
// cout<<base.v[i][j]<<' ';
// cout<<'\n';
// }
M ans(0);ans=qpow(a,n);
cout<<ans.v[1][2]%Mod<<'\n';
return 0;
}
例2.走楼梯
有 \(n\) 级台阶,每次可以走 \(1\sim m\) 级,求共有几种方案。对 \(10^9+7\) 取模。
其中 \(1\le n\le 10^{18},1\le m\le 100\)。
这题还能转化为维护一个序列,满足:
注意到 \(n\) 非常大,但 \(m\) 非常小。设 \(f_i\) 表示走到第 \(i\) 级台阶的方案数。
不难想到状态矩阵 \(a\) 为 \([f_i,f_{i+1}\cdots f_{i+m-1}]\),这可以用 \(O(m^2)\) 暴力求出,或用前缀和优化下 \(O(m)\)。但问题不大。
接下来构造转移矩阵。
先看看目标:
注意到 \(\forall 1\le j< m,f_i\rightarrow f_{i+1}\),那么这一列就仅有 \(j+1\) 行为 \(1\),其余为 \(0\)。
特别的,\(f_{i+m}=\sum_{j=1}^m f_{i+j-1}\),所以转移矩阵的最后一列全为 \(1\)。
那么这题的步骤就是:
- 暴力搞出初始矩阵
- \(O(m^2)\) 求出转移矩阵
- 快速幂
最后特判一下,如果 \(n\le m\),则不用快速幂,直接输出初始矩阵内的元素。
代码:
#include<bits/stdc++.h>
using namespace std;
using ljl = long long;
const ljl N=1e18+5;
const int M=105,Mod=1e9+7;
ljl n;int m;
struct Matrix{
ljl v[M][M];
Matrix(int x)
{
memset(v,0,sizeof(v));
for(int i=1;i<M;++i)
v[i][i]=x;
}
}base(1),ans(0);
Matrix operator * (const Matrix &a,const Matrix &b)
{
Matrix ans(0);
for(int i=1;i<=m;++i)
for(int j=1;j<=m;++j)
for(int k=1;k<=m;++k)
ans.v[i][j]=(ans.v[i][j]%Mod+a.v[i][k]%Mod*b.v[k][j]%Mod)%Mod;
return ans;
}
Matrix qpow(Matrix a,ljl p)
{
Matrix ans(1);
while(p)
{
if(p&1)ans=ans*a;
a=a*a;
p>>=1;
}
return ans;
}
int main(){
// ios::sync_with_stdio(0);
cin>>n>>m;
for(int i=1;i<=m;++i)
{
ans.v[1][i]=1;
for(int j=1;j<i;++j)
ans.v[1][i]=(ans.v[1][i]+ans.v[1][j])%Mod;
}
if(n<=m)
{
cout<<ans.v[1][n]<<'\n';
return 0;
}
// for(int i=1;i<=m;++i)
// cout<<ans.v[1][i]<<' ';
// cout<<'\n';
Matrix fac(0);
for(int i=1,cnt=2;i<=m;++i)//lie
{
if(i!=m)
{
fac.v[cnt][i]=1;
++cnt;
}
else
{
for(int j=1;j<=m;++j)
fac.v[j][i]=1;
}
}
// for(int i=1;i<=m;++i)
// {
// for(int j=1;j<=m;++j)
// cout<<fac.v[i][j]<<' ';
// cout<<'\n';
// }
Matrix tmp=qpow(fac,n-m);
// cout<<"111\n";
ans=ans*tmp;
cout<<ans.v[1][m]%Mod<<'\n';
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号