[算法日常] 分层图最短路
[算法日常] 分层图最短路
定义
对于一个可以跑最短路的图 \(G\),有 \(k\) 次可以 改变权值 的机会的问题,我们叫它分层图最短路。
前置知识
- 最短路(建议使用 dijkstra)
- dp
解法
解法1:二维dp
首先根据 dijkstra 算法中的松弛操作数组 dis[i] 入手,原意是表示点 \(i\) 到起点 \(s\) 的最短路。
那么可以多设一维,dis[i][j] 表示节点 \(i\) 用了 \(j\) 次机会时距离 \(s\) 的最短路。
那么在跑最短路的过程中,在松弛操作里,就可以把状态转移方程推一下:
上面意思是松弛操作看看是不用机会好还是用了机会好。
解法2:多建点边
这种方法我认为是最适合萌新(比如我)学的解法。因为它十分好理解。
设我们改变的权值为 \(w\)。
原图可认为是第一层的原图,而此方法是再新建了 \(k\) 层,每层对应的节点用 \(w\) 连接。
例子:
假设我们有这么一张图:
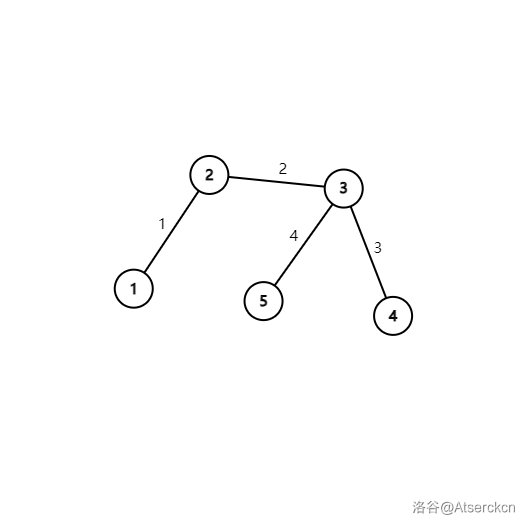
其中 \(k=1\)。
那么我们建的图就是这样的:

十分抽象
注意到,我们真正的节点仅有 \(1\sim 5\),而我们却建了 \(1\sim k\times n\),共 \(k\) 层,中间用可修改的权值连接。
且对应的 \(i\times n+u\) 连接的肯定是对应的 \((i+1)\times n+v\) 或 \((i-1)\times n+v\)。
这么做也就是分层图的名字来源。
那么很显然了,我们就从 \(s\) 号节点做最短路,跑到我们需要的节点 \(t\),并且再取个 \(min(dis_{1\times n+t}\sim dis_{k*n+t})\)。因为有可能 \(k\) 次机会没有用完。
或者不用取最小值,可以在每个 \(i\times n+t\) 连个 \(w\) 的边。最后直接求 \(dis_{k\times n+t}\)。
易错点
注意边数!!!特别是打链式前向星的同学们(比如我)很经常栽在没建够图上,请算清楚,一共有 \(4\times (k+1)\times n\) 条边!
例题:
[JLOI2011] 飞行路线
显然分层图,且 \(w\) 为 \(0\)。
代码:
#include<bits/stdc++.h>
using namespace std;
#define ljl long long
#define PII pair<ljl,ljl>
#define mk make_pair
const ljl K=15,M=2e6+5,N=(1e4+5)*K,inf=1e18;
ljl n,m,k,head[N],cnt_e,u,v,w,s,t,dis[N],ans;
bool vis[N];
priority_queue <PII ,vector < PII > , greater< PII > > heap;
struct E{
ljl to,w,pre;
}e[M<<1];
inline void add(ljl from,ljl to,ljl w)
{
e[++cnt_e].to=to;
e[cnt_e].w=w;
e[cnt_e].pre=head[from];
head[from]=cnt_e;
return;
}
inline void init()
{
memset(dis,0x3f3f3f3f,sizeof(dis));
memset(vis,0,sizeof(vis));
while(!heap.empty())
heap.pop();
return;
}
inline void dijk()
{
init();
dis[s]=0;
heap.push(mk(0,s));
while(!heap.empty())
{
ljl u=heap.top().second;
heap.pop();
if(vis[u]) continue;
vis[u]=true;
for(ljl i=head[u];i;i=e[i].pre)
{
ljl v=e[i].to;
if(dis[v]>dis[u]+e[i].w)
{
dis[v]=dis[u]+e[i].w;
heap.push(mk(dis[v],v));
}
}
}
return;
}
int main(){
scanf("%lld%lld%lld",&n,&m,&k);
scanf("%lld%lld",&s,&t);
for(ljl i=1;i<=m;i++)
{
scanf("%lld%lld%lld",&u,&v,&w);
add(u,v,w);add(v,u,w);
//重点建图!!!!!!
for(ljl j=1;j<=k;j++)//往下建k层
{
add(u+(j-1)*n,v+j*n,0);
add(v+(j-1)*n,u+j*n,0);
add(u+j*n,v+j*n,w);
add(v+j*n,u+j*n,w);
}
}
for(ljl i=1;i<=k;i++)//上述,最后直接取最小值即可,不用考虑是否用完k次机会
add(t+(i-1)*n,t+i*n,0);
dijk();
printf("%lld\n",dis[t+k*n]);
return 0;
}
[BJWC2012] 冻结
解题思路显然,不过唯一不同就是修改的边权不是 \(0\),而是 \(\frac{w}{2}\)。
#include<bits/stdc++.h>
using namespace std;
#define ljl long long
#define PII pair<ljl,ljl>
#define mk make_pair
const ljl K=25,M=5e6+5,N=(1e4+5)*K,inf=1e18;
ljl n,m,k,head[N],cnt_e,u,v,w,s,t,dis[N],ans;
bool vis[N];
priority_queue <PII ,vector < PII > , greater< PII > > heap;
struct E{
ljl to,w,pre;
}e[M<<1];
inline void add(ljl from,ljl to,ljl w)
{
e[++cnt_e].to=to;
e[cnt_e].w=w;
e[cnt_e].pre=head[from];
head[from]=cnt_e;
return;
}
inline void init()
{
memset(dis,0x3f3f3f3f,sizeof(dis));
memset(vis,0,sizeof(vis));
while(!heap.empty())
heap.pop();
return;
}
inline void dijk()
{
init();
dis[s]=0;
heap.push(mk(0,s));
while(!heap.empty())
{
ljl u=heap.top().second;
heap.pop();
if(vis[u]) continue;
vis[u]=true;
for(ljl i=head[u];i;i=e[i].pre)
{
ljl v=e[i].to;
if(dis[v]>dis[u]+e[i].w)
{
dis[v]=dis[u]+e[i].w;
heap.push(mk(dis[v],v));
}
}
}
return;
}
int main(){
scanf("%lld%lld%lld",&n,&m,&k);
s=1,t=n;
for(ljl i=1;i<=m;i++)
{
scanf("%lld%lld%lld",&u,&v,&w);
add(u,v,w);add(v,u,w);
for(ljl j=1;j<=k;j++)
{
add(u+(j-1)*n,v+j*n,w/2);
add(v+(j-1)*n,u+j*n,w/2);
add(u+j*n,v+j*n,w);
add(v+j*n,u+j*n,w);
}
}
for(ljl i=1;i<=k;i++)
add(t+(i-1)*n,t+i*n,0);
dijk();
printf("%lld\n",dis[t+k*n]);
return 0;
}
是的,我压根就没有重新打代码,就是改了一些细节。
总结
分层图最短路实现不难,难在它的思路以及变通。之所以从 提高+/省选- -> 普及+/提高 可能就是因为 CCF 今年重视了思路应用,而不是代码实现吧。。
预祝大家 CSP-J/S 2024 RP++!!!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号