次小生成树
次小生成树
前置知识:
- 图论
- 最小生成树
- 倍增求LCA
概念
次小生成树,分为严格次小生成树和非严格次小生成树。
一下设图为 \(G\),最小生成树为 \(T\),非严格次小生成树为 \(T'\),严格次小生成树为 \(T''\)。
非严格次小生成树:在图 \(G\) 的所有除了 \(T\) 的生成树中,最小的那个。即 \(T'\ge T\)。
严格次小生成树:在 \(G\) 的除了 \(T\) 的生成树中,最小的大于 \(T\) 的生成树。即 \(T''>T\)。
例题
解法:
想要求解(非)严格次小生成树,那么首先肯定需要建出最小生成树,然后在 \(T\) 上面修改。
假设我们已经建出 \(T\):
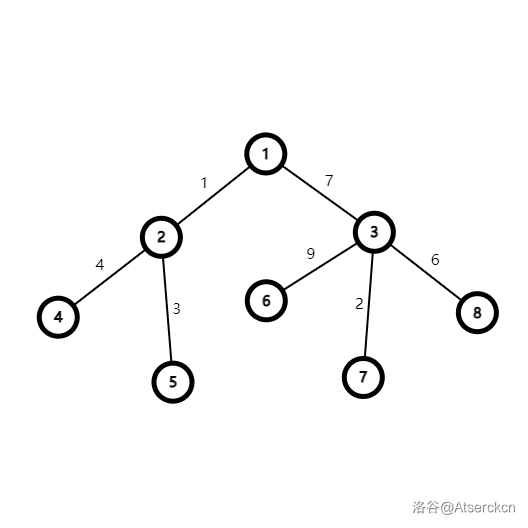
首先可以想到,若要将 \(T\) 改为 \(T'\) 或 \(T''\),仅需在 \(T\) 上面修改一条边。
那么我们就可以枚举非树边,尝试将其插入进去。
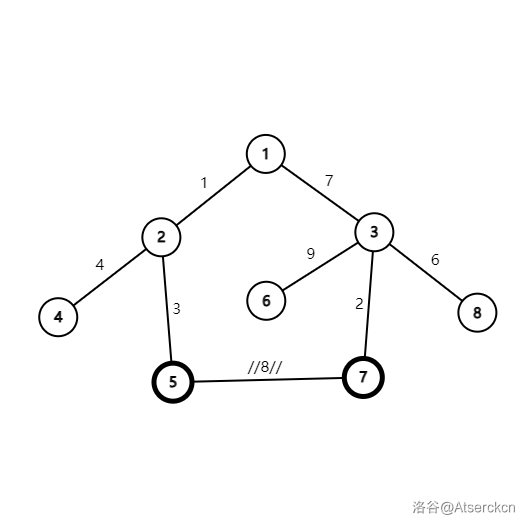
- 加入了 \(5\rightarrow 7\),长度为 \(8\) 的非树边。
那么如果加入了一条边,肯定会构成环。\((n-1+1)=n\)。
上图即出现了环:
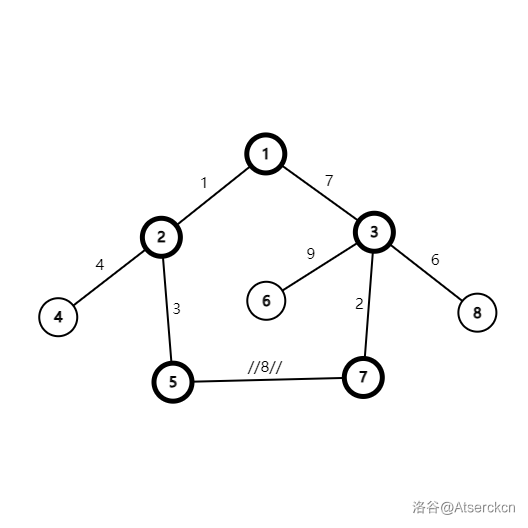
那么,上面的环中,除了 \(5\rightarrow 7\) 的这条外,就是 \(1\rightarrow 3\) 的这条边最大。而要想要建出次小生成树,则需要在环中,删除除了新加入的非树边外,最大的那一条。因为如果不是最大的,则生成出来的就不能保证是次小的。
当我们将 \(1\rightarrow 3\) 删去后,就组成了一个新的生成树,即为非严格次小生成树——
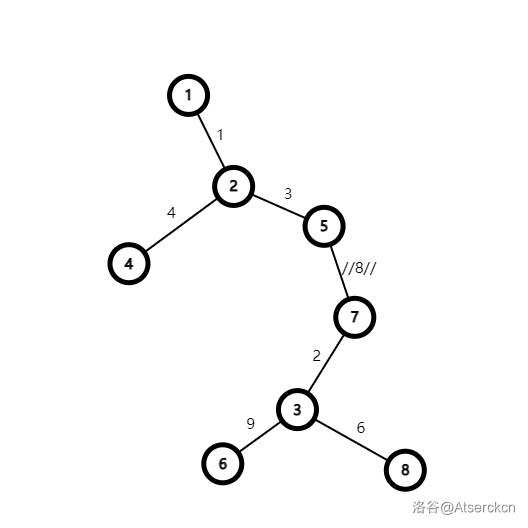
得到的,即为非严格次小生成树。
注意到,我的用词为非严格,那么就说明还没有结束 _
如果是非严格次小生成树,那么到这里就可以了,再见。因为 \(T'\ge T\),处理到这里就行了。
但是我们需要考虑一个很烦人的情况:如果最大边等于非树边咋办?
别急,往下看 _
环上最大权值
那么如何求解环上的最大边呢?
设 \(x\) 和 \(y\) 为新增边的两个端点。
不难想到,可以比较路径 \(x\rightarrow lca(x,y)\) 和 \(y\rightarrow lca(x,y)\) 的路径上的最大和次大值。
这里讲解用 LCA 的倍增求解。
跟LCA相似,用 lca[u][i] 表示点 u 向上跳 \(2^i\) 层后到达的节点。
设 max1[u][i] 和 max2[u][i] 分别表示 u 向上跳 \(2^i\) 层路上的最大和次大边。
那么跟 LCA 一样,lca 数组的处理方式不细说了,详见此。
最后,比较一下 max1[x][lca(x,y)] 和 max1[y][lca(x,y)] 的最大边即为 \(x\rightarrow y\) 路径上的最大边。
那么。。。
你的。。。
max2 数组。。。
用来。。。
干什么。。
对,当然没结束!!
还记得吗,我说的那句话——
但是我们需要考虑一个很烦人的情况:如果最大边等于非树边咋办?
为了解决这个情况,max2 数组就派上用场啦。
max2 数组的维护与倍增几乎与 max1 数组一样,待会儿自己看代码理解吧。。
因为次小生成树的重点在于环上最大/次大值,所以最小生成树和 LCA 的代码我不会讲解。
代码实现
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5,M=3e5+5;
const int inf=1e9+5;
int n,m,u,v,w,f[N],cnt_edge,head_edge[N],dep[N],lca[N][22],max1[N][22],max2[N][22],minn=inf;//minn为最大/次大值
ll ans;
int findfa(int x)
{
return f[x]==x?x:f[x]=findfa(f[x]);
}
inline void Union(int x,int y)
{
f[findfa(x)]=findfa(y);
return;
}
struct E{
int from,to,w,pre;
bool vis;
bool operator < (const E &other)//排序需要
{
return w<other.w;
}
}e[M<<1],edge[M<<1];
inline void add_edge(int from,int to,int w)//最爱的链式前向星存图~~
{
edge[++cnt_edge].from=from;
edge[cnt_edge].to=to;
edge[cnt_edge].w=w;
edge[cnt_edge].pre=head_edge[from];
head_edge[from]=cnt_edge;
return;
}
inline void kruskal()//最小生成树
{
sort(e+1,e+m+1);
int cnt_vis=0;
for(int i=1;i<=m;i++)
{
int u=e[i].from,v=e[i].to,w=e[i].w;
if(findfa(u)!=findfa(v))
{
Union(u,v);
++cnt_vis;
add_edge(u,v,w);
add_edge(v,u,w);
e[i].vis=true;
ans+=w;
if(cnt_vis>=n-1)
return;
}
}
return;
}
void dfs(int u)//开始预处理u
{
for(int i=head_edge[u];i;i=edge[i].pre)
{
int v=edge[i].to;
if(v==lca[u][0])continue;
lca[v][0]=u;//设置父亲节点
dep[v]=dep[u]+1;//深(gong)度(de)+1
max1[v][0]=edge[i].w;//此边即为最大边(目前)
for(int j=1;j<=20;j++)
{
//分割线
//一下为求解lca的正常步骤
if(dep[v]<(1<<j))
break;
lca[v][j]=lca[lca[v][j-1]][j-1];
max1[v][j]=max(max1[v][j-1],max1[lca[v][j-1]][j-1]);
//分割线
if(max1[v][j-1]==max1[lca[v][j-1]][j-1])//如果最大值没变
max2[v][j]=max(max2[v][j-1],max2[lca[v][j-1]][j-1]);//更新次大值
else//否则就!#@$%^&*^%$(叽里呱啦)
{
max2[v][j]=min(max1[v][j-1],max1[lca[v][j-1]][j-1]);
max2[v][j]=max(max2[v][j],max2[lca[v][j-1]][j-1]);
max2[v][j]=max(max2[v][j],max2[v][j]);
}
}
dfs(v);
}
return;
}
inline int getlca(int u,int x)//函数如其名
{
if(dep[u]<dep[x])
swap(u,x);
for(int i=20;i>=0;i--)
if(dep[lca[u][i]]>=dep[x])
u=lca[u][i];
if(u==x)
return u;
for(int i=20;i>=0;i--)
if(lca[u][i]!=lca[x][i])
u=lca[u][i],x=lca[x][i];
return lca[x][0];
}
inline void change(int u,int fa,int w)//这就是求解最大/次大值
{
int maxn1=0,maxn2=0;
int d=dep[u]-dep[fa];
for(int i=0;i<=20;i++)//向上倍增求解
{
if(d<(1<<i))
break;
if(d&(1<<i))
{
if(max1[u][i]>maxn1)
{
maxn2=max(maxn1,max2[u][i]);
maxn1=max1[u][i];
}
u=lca[u][i];
}
}
if(w!=maxn1)
minn=min(minn,w-maxn1);
else
minn=min(minn,w-maxn2);
return;
}
inline void solve()//开始枚举边,进行插入进MST中
{
for(int i=1;i<=m;i++)
{
if(e[i].vis) continue;
int x=e[i].from,y=e[i].to,w=e[i].w,LCA=getlca(x,y);
if(x==y) continue;
change(x,LCA,w);change(y,LCA,w);
}
return;
}
signed main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
f[i]=i;
for(int i=1;i<=m;i++)
scanf("%d%d%d",&e[i].from,&e[i].to,&e[i].w);
kruskal();
dfs(1);
solve();
printf("%lld\n",ans+minn);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号