FWT
\(FFT\)（快速傅里叶变换）求的是卷积，也就是
\[C_k=\sum_{i+j=k}A_iB_j
\]
那么\(FWT\)（快速沃尔什变换）求的就是子集卷积，也就是
\[C_{k}=\sum_{i \oplus j=k} A_{i} B_{j}
\]
\(\oplus\)指按位运算\(or,and,xor\)
其实\(or,and\)卷积应该是\(FMT\)（快速莫比乌斯变换），因为思想较为类似，故写在一篇博客中。
\(FMT\)
先介绍\(or\)卷积，因为感性上理解\(or\)和\(and\)操作较为类似，所以两者实际是等价的。
根据\(FFT\)的思路，我们同样需要变换出一个函数使得
\[FMT(A)_i\times FMT(B)_i=FMT(C)_i
\]
然后莫比乌斯变换就是构造了下面这个式子：
\[FMT(A)_n=\sum _{i \subseteq n}A_i
\]
证明也很简单：
\[\sum_{i \subseteq n} A_{i} \sum_{j \subseteq n} B_{j}=\sum_{i, j \subseteq n} A_{i} B_{j}=\sum_{k \subseteq n} \sum_{i | j=k} A_{i} B_{j}
\]
注意到
\[C_k=\sum_{i\oplus j = k}A_iB_j
\]
那么
\[FMT(A)_n\times FMT(B)_n=\sum_{k\subseteq n}C_k=FMT(C)_n
\]
于是我们需要快速地求出子集和。
有两种主要的方法，一种是高维前缀和，可以看这里。
另一种是分治的算法，借一张网上的图，箭头表示累加，应该就能理解了。
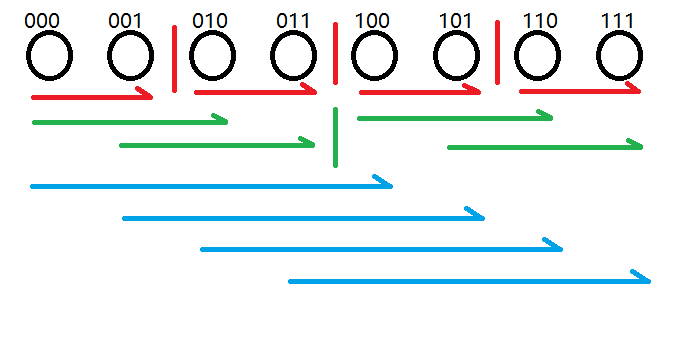
变回去是把累加改为减就可以了。
代码如下：
void FMT(int *a, int n, int x)
{
for (int i = 1; i <= 1 << n; i <<= 1)
for (int j = 0; j < 1 << n; j += (i << 1))
for (int k = 0; k < i; ++k)
a[i + j + k] += a[j + k] * x;
}
\(and\)卷积也很类似
\[FMT(A)_n=\sum_{n\subseteq i}A_i
\]
代码如下：
void FMT(int *a, int n, int x)
{
for (int i = 1; i <= 1 << n; i <<= 1)
for (int j = 0; j < 1 << n; j += (i << 1))
for (int k = 0; k < i; ++k)
a[j + k] += a[i + j + k] * x;
}
时间复杂度\(O(n2^n)\)
\(FWT\)
\(xor\)卷积相对复杂一些，主体思路也是构造函数使得：
\[FWT(A)_i\times FWT(B)_i=FWT(C)_i
\]
先丢一个结论：
\[FWT(A)_i=\sum_{k=0}^{n}(-1)^{|i\bigcap k|}A_k
\]
（\(\bigcap\)即\(c++\)中的\(\&\)，后文以\(\&\)代替）
我们来尝试构造一下：
\[FWT(A)_i=\sum_{k=0}^{n}g(i,k)A_k
\]
\[\sum_{x=0}^{n} g(i, x) \sum_{j \oplus k=x} A_{j} B_{k}=\sum_{j=0}^{n} g(i, j) A_{j} \sum_{k=0}^{n} g(i, k) B_{k}
\]
\[\sum_{j=0}^{n} \sum_{k=0}^{n} g(i, j \bigoplus k) A_{j} B_{k}=\sum_{j=0}^{n} \sum_{k=0}^{n} g(i, j) g(i, k) A_{j} B_{k}
\]
即使得：
\[g(i,j)g(i,k)=g(i,j\bigoplus k)
\]
注意到一个性质：\(|j|+|k|\)与\(|j \bigoplus k|\)奇偶性相同（二进制为\(1\)的位数）
所以尝试\(g(i,j)=(-1)^{|i\& j|}\)
正确性显然，因为\((j\& i)\bigoplus (k\& i)=(j\bigoplus k)\& i\)
于是我们就得到了上面的结论：
\[FWT(A)_i=\sum_{k=0}^{n}(-1)^{|i\& k|}A_k
\]
如何求？
正变换时：
\[\begin{array}{c}{A_{j+k}=A_{j+k}+A_{j+i+k}} \\ {A_{j+i+k}=A_{j+k}-A_{j+i+k}}\end{array}
\]
逆变换由上式可以得出：
\[\begin{array}{c}{A_{j+k}=\frac{A_{j+k}+A_{j+i+k}}{2}} \\ {A_{j+i+k}=\frac{A_{j+k}-A_{j+i+k}}{2}}\end{array}
\]
如何理解？
\(i\)即为第\(i\)数位取不取，设\(i\)取为\(A\)，\(i\)不取为\(B\)，考虑贡献时，\(A\& A,B\&B, A\& B, B\&A\)中，只有\(A\&B\)比原数\(A\)少一位，贡献为\(-1\)（即\(A_{j+i+k}\)对\(A_{j+i+k}\)的贡献），其余贡献都为\(1\)。
void FWT(int *a, int n, int x)
{
for (int i = 1; i < 1 << n; i <<= 1)
for (int j = 0; j < (1 << n); j += (i << 1))
for (int k = 0; k < i; ++k)
{
int x = a[j + k];
int y = a[i + j + k];
a[j + k] = x + y;
a[i + j + k] = x - y;
if (!~x)
{
a[i + j] >>= 1
a[i + j + k] >>= 1;
}
}
}
时间复杂度\(O(n2^n)\)
模板题
三种操作都囊括了。
//by OIerC
//Forca Barcelona!
#include<cstdio>
using namespace std;
const int N = 1 << 17, P = 998244353, inv_2 = 499122177;
inline int add(int a, int b){return a + b >= P ? a + b - P : a + b;}
inline int sub(int a, int b){return a - b < 0 ? a - b + P : a - b;}
inline int mul(int a, int b){return 1ll * a * b - 1ll * a * b / P * P;}
int a[N], b[N], c[N];
inline int read()
{
int x = 0, f = 1; char ch = getchar();
for (; ch < '0' || ch > '9'; ch = getchar()) if (ch == '-') f = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 1) + (x << 3) + ch - '0';
return x * f;
}
inline void FWTor(int *a, int n, int t)
{
for (register int i = 1; i < n; i <<= 1)
for (register int j = 0; j < n; j += (i << 1))
for (register int k = 0; k < i; ++k)
if (~t) a[i + j + k] = add(a[i + j + k], a[j + k]);
else a[i + j + k] = sub(a[i + j + k], a[j + k]);
}
inline void FWTand(int *a, int n, int t)
{
for (register int i = 1; i < n; i <<= 1)
for (register int j = 0; j < n; j += (i << 1))
for (register int k = 0; k < i; ++k)
if (~t) a[j + k] = add(a[j + k], a[i + j + k]);
else a[j + k] = sub(a[j + k], a[i + j + k]);
}
inline void FWTxor(int *a, int n, int t)
{
for (register int i = 1; i < n; i <<= 1)
for (register int j = 0; j < n; j += (i << 1))
for (register int k = 0; k < i; ++k)
{
int x = a[j + k], y = a[i + j + k];
a[j + k] = add(x, y);
a[i + j + k] = sub(x, y);
if (!~t)
a[j + k] = mul(a[j + k], inv_2),
a[i + j + k] = mul(a[i + j + k], inv_2);
}
}
int main()
{
int n = read(), m = 1 << n;
for (register int i = 0; i < m; ++i) a[i] = read();
for (register int i = 0; i < m; ++i) b[i] = read();
FWTor(a, m, 1); FWTor(b, m, 1);
for (register int i = 0; i < m; ++i) c[i] = mul(a[i], b[i]);
FWTor(a, m, -1); FWTor(b, m, -1); FWTor(c, m, -1);
for (register int i = 0; i < m; ++i) printf("%d ", c[i]); puts("");
FWTand(a, m, 1); FWTand(b, m, 1);
for (register int i = 0; i < m; ++i) c[i] = mul(a[i], b[i]);
FWTand(a, m, -1); FWTand(b, m, -1); FWTand(c, m, -1);
for (register int i = 0; i < m; ++i) printf("%d ", c[i]); puts("");
FWTxor(a, m, 1); FWTxor(b, m, 1);
for (register int i = 0; i < m; ++i) c[i] = mul(a[i], b[i]);
FWTxor(a, m, -1); FWTxor(b, m, -1); FWTxor(c, m, -1);
for (register int i = 0; i < m; ++i) printf("%d ", c[i]); puts("");
return 0;
}
