网络流

概念

网络是特殊的有向图，一般记作 \(G(V,E)\)。
其入度为零的点和出度为零的点均只有一个，分别称为源点（\(s\)）和汇点（\(t\)）。
对于其中的每条有向边，其边权称容量（\(c(u,v),\text{capacity}\)）和流量（\(f(u,v),\text{flow}\)）。

有时候会存在 \((t,s)\) 的边，在某些题中会有体现。
一般情况下，我们并不要求网络流中无环。

一个流被称为可行流，当且仅当：

• 对于 \(\forall u\in V,u\neq s/t,\sum_{(u,v)} f(u,v)=\sum_{(r,u)} f(r,u)\)，即除源点和汇点满足入流量等于出流量（流量守恒原则）。
• 一定有 \(\sum_v f(s,v)=\sum_r f(r,t)\)，即净流出量等于净流入量。
• 满足 \(\forall u,v\in V,0\le f(u,v)\le c(u,v)\)，即每条边的流量禁止超过容量，同时不存在负流。

定义一个可行流的值（\(|f|\)，又称流量）为 \(\sum_v f(s,v)=\sum_r f(r,t)\)。

应当明确，流是网络在不超过容量限制的前提下对于流量的一种构造，而非一条最大路径。
事实上，根据流的分解定理，任意一个可行流都可以分解成几条 \(s\to t\) 的路径和环的组合。

最大流

最大流问题，即对于给定的 \(G\)，求 \(|f|\) 最大的可行流。

Fold-Forkerson

给出一些定义：

• 剩余容量：对于边 \((u,v)\)，定义其剩余容量为 \(c_f(u,v)=c(u,v)-f(u,v)\)。

• 残量网络：由原网络中所有点和剩余容量大于零的边组成的子图 \(G_f(V,E_f)\)。

  注意在 \(G_f\) 中不存在流量，只存在容量。

思考如何判断是否当前最优和如何更新答案。
定义每条边初始流量为零。
显然，如果存在 \(G_f\) 上的路径 \(s\to t\)，显然可以将路径上所有 \(c_f\) 减一以增加答案，将其定义为增广路。

容易想到，每次暴力 dfs 在 \(G_f\) 中找增广路，如果存在就更新 \(G_f\) 和答案。
然而这是一个贪心的做法，难以跑出最优解。

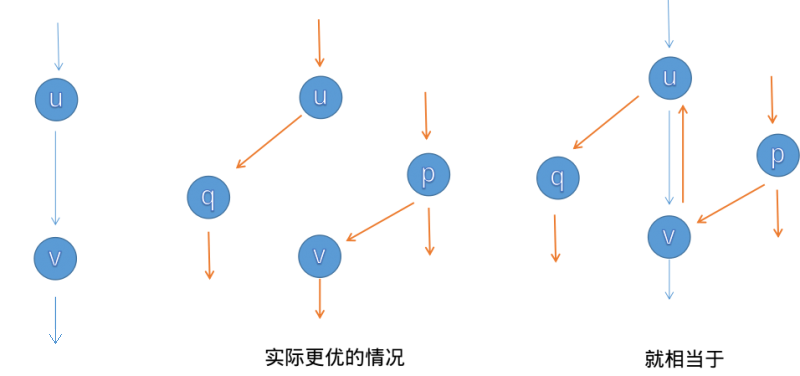
如图（from OI-Wiki），对于 \(G\) 来说，\(c(x,u)=c(v,y)=1\)。
实际的最优解如图二，第一次选后如图一。

按照朴素思路，我们先选了错误的 \((u,v)\)，
接下来我们发现已经不存在其他答案，于是会直接返回。

我们发现当前状态难以描述，无法 dp。
我们能否用"反悔"的思想进行处理？
显然，我们如果已经取过一条边，就可以选择让一个虚拟的负流流回，
这就是一个感性理解的平衡思想。

对应到 \(G_f\) 上面，每次得到一条增广路就会在相应的位置建一组和 \(c_f\) 和增广的 \(|f|\) 相等的反向路径。
如图三，算法最终会找到橙色的增广路并推出。

显然，如果在同一条边上有两条方向相反流量相等的流，
则这两个流可以互相抵消，
即我们得到的答案等价于最优解。

算法证明较为复杂，可能感性理解容易一些。

例如，你和 A 玩游戏，有了反边就相当于有了无限反悔权。
如果这你都赢不了（找到增广路更新答案），显然一定不存在胜利方法（更优解）。

在计算过程中，
可能最终会遇到 \((u,v)\in G_f,c_f(u,v)=0\) 的情况，此时直接将其删除即可。
由于实现复杂度，一般选择在初始时就将所有的边建好。

朴素的 Fold-Fulkerson 算法时间复杂度为 \(O(|E||f|)\)，实际使用极少。

单轮增广 \(O(|E|)\)，至多 \(O(|f|)\) 轮。

Edmonds-Karp & Dinic

• Edmonds-Karp 算法
  为了避免 DFS 的无效搜索，自然想到 BFS。（考虑迭代加深的例子）
  显然每次没有必要加一，可以直接加 \(\Delta=\min\limits_{(u,v)\in A} c_k(u,v)\)，其中 \(A\) 代表增广路边集。
  最终其对答案贡献即为 \(\Delta\)。
  找反向边一般采取编号连续的链式前向星，可以用位运算简化表达。

  时间复杂度 \(O(|V||E|^2)\)，稀疏图效率较高。

  简而言之，Fold-Fulkerson + 每次更新不止一。

• Dinic 算法
  考虑用 BFS 对原图进行分层。
  定义每个点的层数为其到源点的最小距离。
  类似 BFS 的，我们令当前求出的流层数由小到大流动，即不考虑从高层向低层的边。

  接下来考虑每次找到一个当前的阻塞流（\(f_b\)）。

  阻塞流，指极大的增广流，即在当前网络中无法再次扩展的一个增广流。
  正如我们前面所说，其是许多条增广路的并。
  显然，一个合法的 \(f_b\) 必然阻塞了所有当前 \(s\to t\) 的路径并饱和了其中的一条。

  然后将 \(f_b\) 加入到 \(f\) 中，重复操作，直到不存在增广路。

  我们由于分层去做，实际上是借用 BFS 的思路而采取了更直接的 DFS。
  而在回溯的过程中，我们一步步继续寻找阻塞流，最终找到答案。

到此，请看例子。

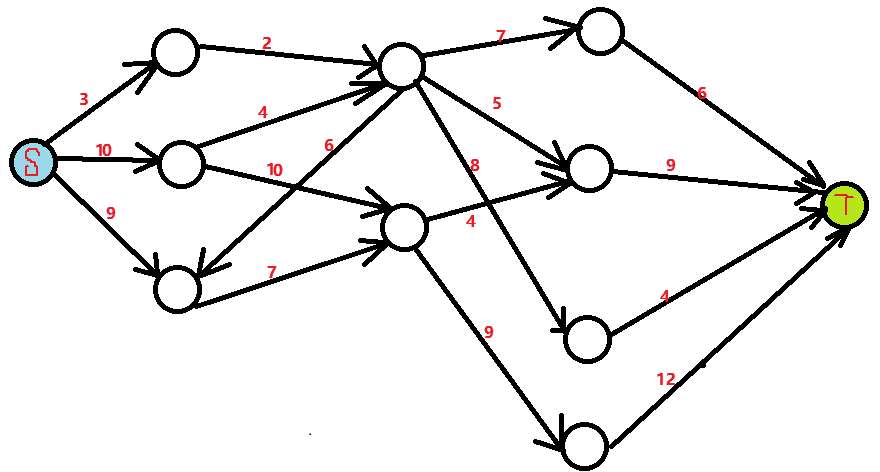
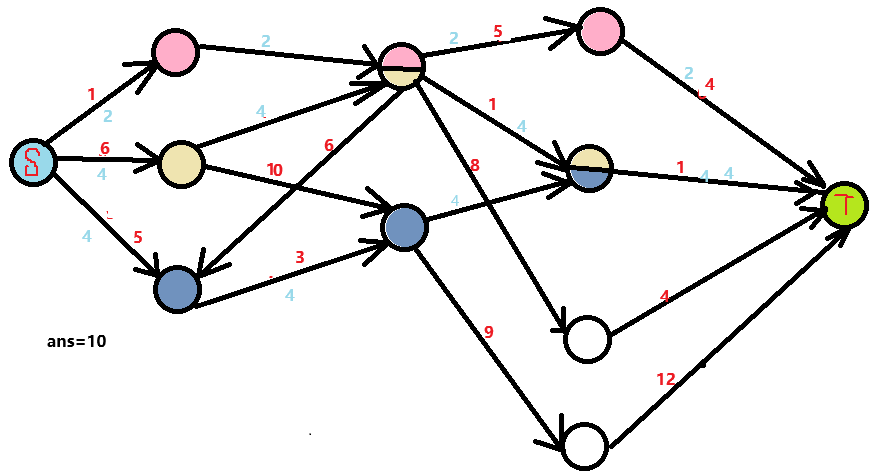
• EK Algorithm（蓝色为反边边权）

三轮 EK 后。

再次 EK（5-3-9-12 chain）

• Dinic Algorithm

半次 Dinic

upd 图片并继续完成第一次 Dinic

我们重新画一下图，开第二次 Dinic，bfs 的层用颜色标记。

标记边，第三次 Dinic。

由上，相信你大概理解了EK 和 Dinic 算法的大致思想。
我们回到 Dinic。
这个算法还有一个重要的部分：当前弧优化。
即对于每一次 Dinic 的过程记录其所在出边位置，以避免重复搜索。
注意在下一次 BFS 分层的时候要将当前弧重置。
理论时间复杂度 \(O(|V|^2|E|)\)，二分图 \(O(\sqrt{|V|}|E|)\)。

不要写引用形式当前弧优化！
会导致代码慢 30 倍！

//Edmonds-Karp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=207,M=5007;
const ll inf=1e14;
int n,m,s,t,h[N],go[N],lineid[N],cnt=-1,q[N],ff,tt; bool flg[N]; ll lim[N];
struct node{int v,nxt; ll w; node(){} node(int _v,ll _w,int _nxt){v=_v,w=_w,nxt=_nxt;}} o[M<<1];
inline void add(int u,int v,ll w){o[++cnt]=node(v,w,h[u]),h[u]=cnt;}
inline ll bfs(){
	ff=0,tt=-1,memset(flg,0,sizeof flg);
	int top; q[++tt]=s,flg[s]=1,lim[s]=inf; //Add S to queue.
	while(ff<=tt){
		top=q[ff++];
		for(int i=h[top];~i;i=o[i].nxt){
			if(o[i].w==0||flg[o[i].v]) continue;
      //Mark Pre-Node and Line-Id in order to change line capacity.
			go[o[i].v]=top,lineid[o[i].v]=i,lim[o[i].v]=min(lim[top],o[i].w);
			if(o[i].v==t) return lim[t];
			q[++tt]=o[i].v,flg[o[i].v]=1; //Mark the node in queue.
		}
	}
	return 0; 
}
int main(){
	int u,v,w; ll ans=0,tmp,x;
	scanf("%d%d%d%d",&n,&m,&s,&t);
	for(register int i=1;i<=n;i++) h[i]=-1;
	for(register int i=1;i<=m;i++) scanf("%d%d%d",&u,&v,&w),add(u,v,w),add(v,u,0);
	while(tmp=bfs()){
		if(!tmp) break; ans+=tmp,x=t;
		while(x!=s) o[lineid[x]].w-=tmp,o[lineid[x]^1].w+=tmp,x=go[x];
	}
	printf("%lld\n",ans);
	return 0;
}

//Dinic
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=209,M=5009;
const ll inf=1e14;
int n,m,s,t,h[N],H[N],cnt=-1,lv[N],q[N],ff,tt; bool flg[N];
struct node{int i,nxt; ll w; node(){} node(int _i,int _nxt,ll _w){i=_i,nxt=_nxt,w=_w;}} o[M<<1];
inline void add(int u,int v,ll w){o[++cnt]=node(v,h[u],w),h[u]=cnt;}
bool bfs(){
	int f;
	memset(flg,0,sizeof flg),lv[s]=lv[t]=0,ff=tt=0,q[0]=s,flg[s]=1;
	for(int i=1;i<=n;i++) H[i]=h[i]; //Reset.
	while(ff<=tt){
		f=q[ff++];
		for(int i=h[f];~i;i=o[i].nxt) if(flg[o[i].i]==0&&o[i].w>0) lv[o[i].i]=lv[f]+1,flg[o[i].i]=1,q[++tt]=o[i].i;
	}
	return lv[t]!=0;
}
ll dfs(int i,ll lim){
	if(i==t||lim==0) return lim; ll ans=0,tmp;
	for(int it=H[i];~it&&lim>0;it=o[it].nxt) if(o[it].w>0&&lv[i]+1==lv[o[it].i])
		H[i]=it,tmp=dfs(o[it].i,min(lim,o[it].w)),o[it].w-=tmp,o[it^1].w+=tmp,lim-=tmp,ans+=tmp;
	return ans;
}
int main(){
	int u,v; ll w,ans=0; scanf("%d%d%d%d",&n,&m,&s,&t); for(int i=1;i<=n;i++) h[i]=-1;
	for(int i=1;i<=m;i++) scanf("%d%d%lld",&u,&v,&w),add(u,v,w),add(v,u,0);
	while(bfs()) ans+=dfs(s,inf);
	printf("%lld\n",ans);
	return 0;
}

ISAP

思考每次 Dinic 都要 BFS 扫一次图。
考虑在 DFS 的过程中就优化掉重新建图的步骤。
这就是 ISAP 的思想。

1. 对反图进行一次 BFS，记录距离 \(d(x)\)。
2. 从源点到汇点进行倒序搜索。
   用循环代替递归优化时间复杂度，
   考虑每步记录前驱节点便于回溯。
   如果已经到达了 \(t\) 就回溯并处理 \(c_f\)。
   否则对于所有的边尝试进行更新（使用当前弧优化）。
   如果发现所有边都已经无法更新，说明我们当前 \(d\) 函数下已经无法进行更新。
   此时我们就选择更新 \(d\) 并回溯，注意此时由于已经修改了其可达性故要重置当前节点的当前弧。

更新为 \(d(u)=\min\limits_{(u,v)\in E} \min d(v)+1\)。
关于回溯，常用的方法是记录对应边的编号。
这样就可以通过走反向边回到上一个位置。

4. 更新 \(d\) 函数时记录当前的每一层数量。
   如果发现更新后原所在层不存在其他元素就直接退出。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int M=5009,N=209;
int n,m,s,t,ocnt=-1,h[N],H[N],d[N],lst[N],cnt[N]; queue<int> q; bool flg[N];
struct _{int i,nxt; ll w;}o[M<<1];
inline void add(int u,int v,ll w){o[++ocnt]=(_){v,h[u],w},h[u]=ocnt;}
void bfs(){
	int u; ll tmp=0,ans=0;
	for(int i=1;i<=n;i++) d[i]=n+1;
	q.push(t),flg[t]=1,d[t]=0;
	while(!q.empty()){
		u=q.front(),q.pop();
		for(int it=h[u],v;~it;it=o[it].nxt) if(!flg[v=o[it].i]) flg[v]=1,q.push(v),d[v]=d[u]+1;
	}
	for(int i=1;i<=n;i++) ++cnt[d[i]];
}
bool Relable(int u){
	H[u]=h[u]; int tmp=n+1;
	for(int it=h[u];~it;it=o[it].nxt) if(o[it].w>0) tmp=min(tmp,d[o[it].i]+1);
	if(--cnt[d[u]]==0) return 0;
	d[u]=tmp,++cnt[d[u]]; return 1;
} 
int main(){
	ll ans=0,num; 
	scanf("%d%d%d%d",&n,&m,&s,&t);
	for(int i=1;i<=n;i++) h[i]=-1;
	for(int i=1,u,v,w;i<=m;i++) scanf("%d%d%d",&u,&v,&w),add(u,v,w),add(v,u,0);
	for(int i=1;i<=n;i++) H[i]=h[i]; bfs();
	for(int u=s;d[s]<n;){
		if(u==t){
			num=LLONG_MAX;
			for(int i=t;i!=s;i=o[lst[i]^1].i) num=min(num,o[lst[i]].w);
			for(int i=t;i!=s;i=o[lst[i]^1].i) o[lst[i]].w-=num,o[lst[i]^1].w+=num;
			ans+=num,u=s; goto done;
		}
		for(int &it=H[u],v;~it;it=o[it].nxt) if(o[it].w>0&&d[v=o[it].i]==d[u]-1){lst[v]=it,u=v; goto done;}
		if(!Relable(u)) break; if(u!=s) u=o[lst[u]^1].i; done:;
	}
	printf("%lld\n",ans);
	return 0;
}

Push-Relable & HLPP

即预流推进算法。
此算法允许一个点的入流大于出流，定义超额流 \(e(u)=\sum_{(v,u)\in E} f(v)-\sum_{(u,v)\in E}f(v)\)。
定义一个节点溢出当且仅当 \(e(u)>0\) 且 \(u\not\in\{s,t\}\)。
对于每个节点定义一个高度 \(h(u)\)，规定溢出节点只能向 \(h(v)<h(u)\) 的 \(v\) 推送超额流，
类似 ISAP 的，其在找不到合法后继的情况下会进行 Relable 操作，提升当前节点的高度 \(h(u)\)。
注意：\(s\) 和 \(t\) 不会被 Relable！

高度函数类似 ISAP 的层数，其维护的也是每个点到 \(t\) 的最小距离。
在 Push 操作时，如果对于一个溢出点，其会尝试向一个满足 \((u,v)\in E,c_f(u,v)>0,h(v)+1=h(u)\) 的点推送流量。
每次暴力寻找溢出点 Push，如果高度不合法就 Relable。

1. 初始设 \(h(u)=\begin{cases}|V|\qquad u=s\\0\qquad\text{otherwise.}\end{cases},e(u)=0\)。
2. 进行一次 BFS 维护除源点外每个点到汇点的最小距离。
3. 为了保证源点 \(s\) 能把流推出去，将 \(e(s)\) 设为 \(\sum_{(s,v)\in E}c_f(v)\)，并不考虑高度限制，强制饱和推送。
4. 为了优化时间复杂度，用队列存储溢出点，每次推流后如果溢出就将其加入队列。（不算源汇）
5. 一个溢出的点可能在推流后仍然溢出，此时考虑再次 Relable。
6. 每次推流推送一个 \(\min\{e(u),c_f(u,v)\}\) 的流，如果不存在合适的流就进行 Relable。
7. 如果发现 Relable 后某一层 \(x\) 为空就对于所有 \(h(y)>x\) 将其标记成 \(h(y)=n+1\)。
   相当于其内部的其他信息已经没有意义，不值得再去考虑高度大小了。
8. 只处理高度小于 \(n\) 的节点。

而 HLPP 就是在此基础下将队列替换成优先队列。
每次取高度最大点进行处理。

example

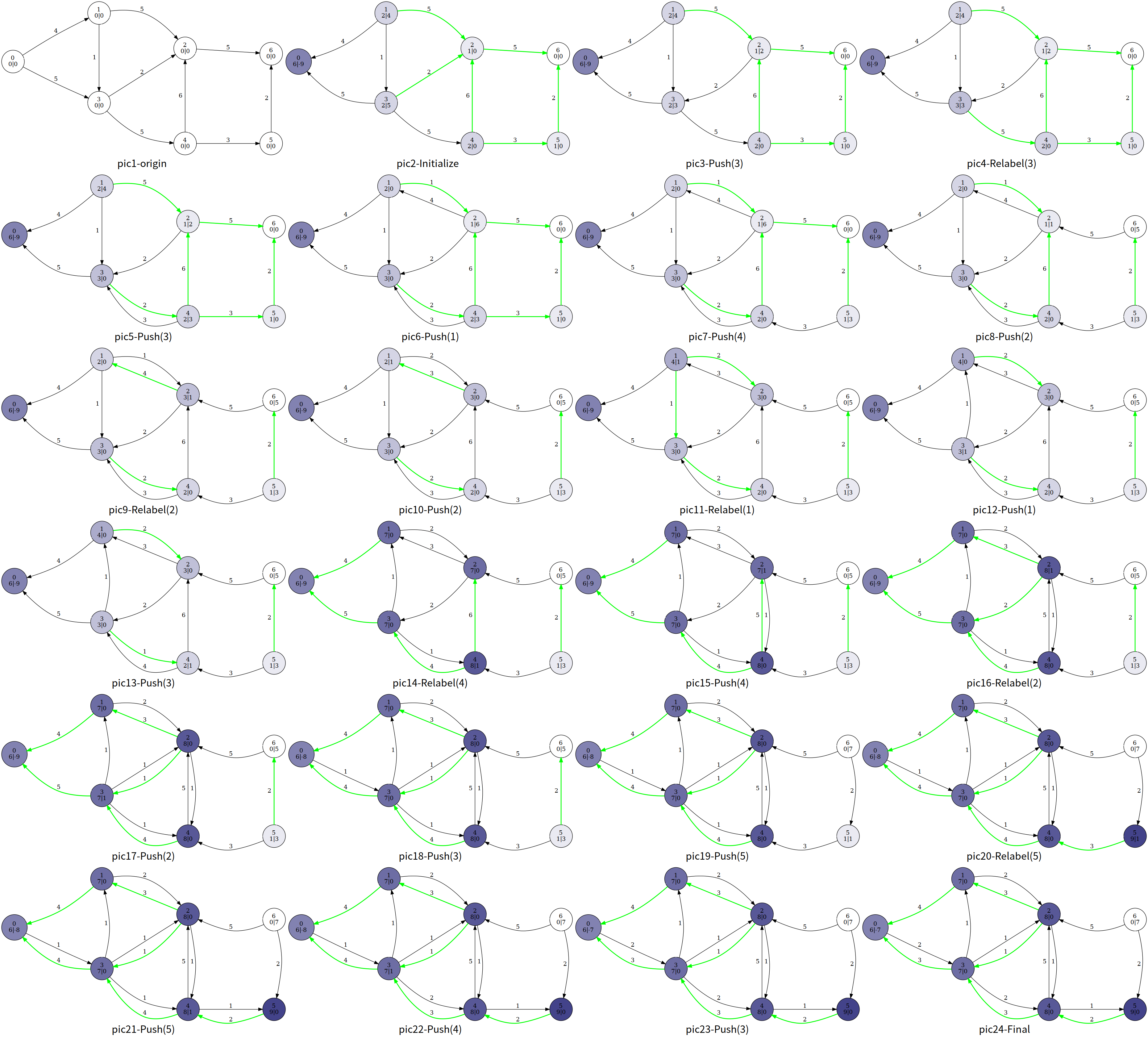
Question：

1. 如何保证每个溢出点经过有限次 Relable 可以用尽所有的额外流？
2. 如何保证在 GAP 优化时每个被提升高度的点都不会有额外流（对于 HLPP 显然，朴素 Push-Relable 呢）？
3. 如何保证所有剩余流都被有效退回？
4. 为什么 Relable 操作不会降低 h?
5. 什么时候用 HLPP？

Answer:

1. 显然额外流是由前驱结点转移而来的。
   根据我们在 Fold-Furkerson 中所讨论过的双向建边可知，只要我们不断回退所得流就可以用尽额外流。

2. 你说得对，所以朴素 Push-Relable 算法不存在 GAP 操作（原操作 7）。
   然而我们并不会写朴素 Push-Relable。

3. 显然，对于 HLPP 算法，当且仅当所有节点都没有剩余流了算法才会结束。
   所以你觉得为什么回不去？

   • 没有足够的 \(c_f\)？
     显然双向边权这是不可能的。
   • GAP 的锅？\(h\) 函数阻塞回归？
     别忘了 \(h\) 函数的定义。
     显然在 GAP 之前其对于 \(t\) 的 BFS 来说是具有一种单调关系的。（指与其联通的节点）
     显然 GAP 处理的都是靠近源点的。
     阻塞回归在 Relable 之后是不可能的。
     这也可以解释为什么有了高度 \(h\) 就不会无限推流。

4. 不，会降低，但不影响。

   每次只可能是减少了一个后继节点才可能进行 Relable。
   容易证明这一定单调不降。

   GAP 之后，确实可能出现降低的情况。
   否则我们为什么不直接在 GAP 之后把他们删掉呢？
   如果还有剩余边，完全可以将其中的剩余流给到汇点。

5. 这个算法稳定性和常数有点抽象，调试难度较高，写反一块轻松调一天。
   建议按需使用。

时间复杂度 \(O(n^2\sqrt m)\)。

#include<bits/stdc++.h>
#define f(i,a,b) for(register int i=a;i<=b;i++)
#define _f(i,u) for(register int i=H[u];~i;i=o[i]._)
using namespace std;
typedef long long ll;
const int N=2009,M=120009,inf=1e7; vector<int> vec[N];
int n,m,s,t,ont=-1,h[N],H[N],lvnt=-1,gap[N]; ll e[N]; struct __{int v,_; ll w;} o[M<<1];
inline void add(int u,int v,ll w){o[++ont]={v,H[u],w},H[u]=ont;}
inline int choose(){while(lvnt>=0&&vec[lvnt].empty()) --lvnt; return (lvnt<0)?0:vec[lvnt].back();}
inline void Relable(int u) {
    int tmp=h[u]; h[u]=inf; _f(it,u) if(o[it].w>0) h[u]=min(h[u],h[o[it].v]+1);
    if(h[u]<n) ++gap[h[u]],lvnt=max(lvnt,h[u]),vec[h[u]].push_back(u); else h[u]=n+1;
    if(tmp<n&&--gap[tmp]==0) f(j,1,n) if(h[j]<n&&h[j]>tmp) --gap[h[j]],h[j]=n+1;
}
int q[N],head=0,tail=-1;
signed main(){
	scanf("%d%d%d%d",&n,&m,&s,&t); int u,v; ll w; for(int i=1;i<=n;i++) H[i]=-1,h[i]=inf;
	f(i,1,m) scanf("%d%d%lld\n",&u,&v,&w),add(u,v,w),add(v,u,0);
	q[++tail]=t,h[t]=0;
	while(head<=tail){u=q[head++]; _f(it,u) if(h[v=o[it].v]==inf&&o[it^1].w) q[++tail]=v,h[v]=h[u]+1;}
	if(h[s]==inf) puts("0"),exit(0); else h[s]=n;
	_f(i,s) if(o[i].w>0&&h[v=o[i].v]<n) lvnt=max(lvnt,h[v]),vec[h[v]].push_back(v),e[v]+=o[i].w,o[i^1].w+=o[i].w,o[i].w=0;
	f(i,1,n) if(h[i]<n) gap[h[i]]++;
	while(u=choose()){
		vec[lvnt].pop_back();
		if(h[u]>n) continue;
		if(u==t) continue;
		_f(it,u){
			if(e[u]==0) break;
			if(o[it].w>0&&h[v=o[it].v]+1==h[u]&&h[v]<n){
				w=min(o[it].w,e[u]),e[u]-=w,e[v]+=w,o[it].w-=w,o[it^1].w+=w;
				if(v==s||v==t) continue; 
				vec[h[v]].push_back(v);
			}
		}
		if(e[u]) Relable(u);
	}
	printf("%lld\n",e[t]);
	return 0;
}

最小割

一个网络的割为：将该网络流的点分成 \(S\) 和 \(T\) 两部分，使得 \(s\in S,t\in T\)。
定义其容量 \(c=\sum_{(u,v)\in E,u\in S,v\in t} c(u,v)\)。
最小割要求一个容量最小的割。

最小割等于最大流。

感性理解即“割断第一条满流边”。
进而对于输出方案就在残量网络中走 \(c_f\) 大于零的边即可。

费用流

对于每条边有一个费用 \(cost(u,v)\)。
一个流流经代价为 \(f(u,v)\times cost(u,v)\)。
求一个费用最小的最大流。

每次走费用和最小的增广路。
用最短路算法代替 Edmonds-Karp 或 Dinic 的 BFS 即可。
注意反向建边费用为负要求使用 SPFA。

//Edmonds-Karp
#include<bits/stdc++.h>
using namespace std;
const int N=5009,M=50009; typedef long long ll; const ll inf=1e15;
struct star{int v,nxt; ll w,c;} o[M<<1]; int n,m,s,t,ont=-1,h[N],pre[N];
inline void add(int u,int v,ll w,ll c){o[++ont]={v,h[u],w,c},h[u]=ont;}
queue<int> q; ll C[N],F[N]; bool vis[N];
int main(){
    int u,v; ll w,c,flow=0,cost=0; scanf("%d%d%d%d",&n,&m,&s,&t); for(int i=1;i<=n;i++) h[i]=-1;
    for(int i=1;i<=m;i++) scanf("%d%d%lld%lld",&u,&v,&w,&c),add(u,v,w,c),add(v,u,0,-c);
    while(true){
        for(int i=1;i<=n;i++) C[i]=inf,vis[i]=0,F[i]=0;
        F[s]=inf,q.push(s),vis[s]=1,C[s]=0;
        while(!q.empty()){
            u=q.front(),q.pop(),vis[u]=0;
            for(int _=h[u];~_;_=o[_].nxt){
                if(o[_].w>0&&C[v=o[_].v]>C[u]+o[_].c){
                    C[v=o[_].v]=C[u]+o[_].c;
                    if(!vis[v]) q.push(v),vis[v]=1;
                    F[v]=min(F[u],o[_].w),pre[v]=_;
                }
            }
        }
        if(C[t]>1e10) printf("%lld %lld\n",flow,cost),exit(0); else flow+=F[t];
        u=t;
        while(u!=s){
           	v=o[pre[u]^1].v;
            cost+=F[t]*o[pre[u]].c;
            o[pre[u]].w-=F[t],o[pre[u]^1].w+=F[t];
            u=v;
        }
    }
    return 0;
}

//Dinic
#include<bits/stdc++.h>
using namespace std;
const int N=5009,M=50009; typedef long long ll; const ll inf=1e15;
struct star{int v,nxt; ll w,c;} o[M<<1]; int n,m,s,t,ont=-1,h[N],H[N],pre[N];
inline void add(int u,int v,ll w,ll c){o[++ont]={v,h[u],w,c},h[u]=ont;}
queue<int> q; ll C[N],flow,cost; bool vis[N];
int dfs(int u,ll w,ll c){
	ll tmp,wlim,sum=0;
	if(u==t){flow+=w; return w;} vis[u]=1; 
	for(int &_=H[u],v;~_&&w>0;_=o[_].nxt){
		if(!vis[v=o[_].v]&&o[_].w>0&&C[u]+o[_].c==C[v]){
			wlim=min(w,o[_].w);
			if(tmp=dfs(v,wlim,c+o[_].c*wlim)) sum+=tmp,o[_].w-=tmp,o[_^1].w+=tmp,w-=tmp,cost+=tmp*o[_].c;
		}
	}
	return sum;
}
int main(){
    int u,v; ll w,c; scanf("%d%d%d%d",&n,&m,&s,&t); for(int i=1;i<=n;i++) h[i]=-1;
    for(int i=1;i<=m;i++) scanf("%d%d%lld%lld",&u,&v,&w,&c),add(u,v,w,c),add(v,u,0,-c);
    while(true){
    	for(int i=1;i<=n;i++) vis[i]=0,C[i]=inf,H[i]=h[i]; q.push(s),C[s]=0,vis[s]=1;
    	while(!q.empty()){
    		u=q.front(),q.pop(),vis[u]=0;
    		for(int _=h[u];~_;_=o[_].nxt) if(o[_].w>0&&C[v=o[_].v]>C[u]+o[_].c){
		    	C[v=o[_].v]=C[u]+o[_].c;
    			if(!vis[v]) vis[v]=1,q.push(v);
			}
		}
		if(C[t]>1e10) printf("%lld %lld\n",flow,cost),exit(0); else dfs(s,inf,0);
	}
    return 0;
}

上下界网络流

为每条边设置容量上界 \(c(u,v)\) 和下界 \(b(u,v)\)。

无源汇可行流

考虑让所有边流满下界，然而未必平衡。
于是建立差网络（不存在下界，同正常网络）\(G'\)，对于任意 \((u,v)\in E,c'(u,v)=c(u,v)-b(u,v)\)。
思考在 \(G'\) 里进行适当的调整以保证平衡。

我们的需求是，对于差网络构造一个可行流 \(f^\star\)，
使得差网络中每个节点的 \(\Delta(u)=\sum_{(v,u)\in E} f(v,u)-\sum_{(u,v)\in E} f(u,v)\) 符合我们的要求（合法的 \(\Delta\) 值根据下界网络求得）。
考虑分讨。

1. \(\Delta=0\)。
   不做处理。
2. \(\Delta<0\)。
   考虑当前想要一个出度更大的流。
   建立虚拟源点 \(S'\) 向 \(u\) 连一条容量为 \(|\Delta|\) 的附加边。
   这样去除附加边后即满足条件。
3. \(\Delta >0\)。
   同理。
   建立虚拟汇点 \(T'\)，从当前点向其连一条容量为 \(\Delta\) 的附加边。

对于下界网络求 \(\Delta\)：
需要出度更大的流，意味着下界网络中入度更大。
显然对于一条下界网络中的边 \((u,v)\)，应将 \(\Delta(u)\) 加上 \(c(u,v)\)，将 \(\Delta(v)\) 减去 \(c(u,v)\)。

最终合法当且仅当所有附加边满流。

实现上，无需建立下界网络，同时也只需判定一侧的附加边即可。
判满流？\(c_f(u,v)=0\)？
其实可以直接判跑出的最大流是否等于所建边的容量和。

有源汇可行流

问题在于，我们不知道 \(s\) 和 \(t\) 在差网络中相当于要额外给多少。
然而我们拥有人类智慧，考虑连一条 \(t\to s\)，且上下界为 \([0,\infty)\) 的边。
显然这一定平衡，可以直接套上面的板子。

有源汇最大流

显然存在最大流当且仅当存在可行流。
考虑先跑可行流。
跑完后，残量网络对应的流就已经能够使得原图平衡。
然而，由于源点和汇点不同，跑可行流时的最大流未必跑出了实际最优解。
于是，我们就删掉所有附加边，然后在保留了原来可行流的图中再跑一次最大流。
两次加和即为答案。

实现时只需删去源汇之间的边即可。
其余附加边由于没有流的去向所以对算法并没有影响。

为了便于实现，一般选择在建好差网络，连好附加边后在去连接源汇。
由于其下界设为了零故不会影响下界网络和差网络上的附加边。

有源汇最小流

同上，考虑第二次从 \(t\) 到 \(s\) 反向求最大流将多余的退回去。
可行减退回即为答案。

上下界最小费用可行流

考虑方法同上。
先统计下界满流费用，
然后在建好额外边的差网络上跑最小费用最大流即可。

不保证所得为最大流。

有负圈的费用流 & 上下界费用流

显然，对于有费用负圈的网络，仍存在最小费用流（容量限制）。
这里给出一种方案，用于一次消去图中所有负权边。
通过上下界网络流算法，使原图中的负权边强制满流。

具体来说，对于一条负权边，进行反向建边（相当于满流），并对其进行补偿性的修正。

if(c>=0) add(u,v,w,c);
else Delta[u]+=w,Delta[v]-=w,add(v,u,w,-c),cost+=w*c;

这并非完全的上下界，用了思路而已。
对于上下界的满流，事实上应当：

if(c>=0) add(u,v,w,c);
else Delta[u]+=w,Delta[v]-=w,_add(u,v,0,c),_add(v,u,0,-c),cost+=w*c;

然而，满流只是借口，消去负边才是目的。
我们未必要让他满流，所以要将反边赋以容量以退流。
这种并非完全上下界的一边惹事一边怕事的建图方式也决定了我们统计答案的特殊方法。

接下来就是跑一遍虚拟源汇的假的上下界可行流。
注意要把残量网络中的费用算上。
注意：如上所说，这个上下界的建图是假的，
所以不能直接算这一次的流值，而是应当：

while(true){
		for(int i=0;i<=T;i++) cur[i]=h[i],vis[i]=0,Dis[i]=inf;
		q.push(S),vis[S]=1,Dis[S]=0;
		while(!q.empty()){
			u=q.front(),q.pop(),vis[u]=0;
			for(int _=h[u];~_;_=o[_].nxt)
				if(Dis[v=o[_].v]>Dis[u]+o[_].c&&o[_].w>0){
					Dis[v]=Dis[u]+o[_].c;
					if(!vis[v]) vis[v]=1,q.push(v);
				}
		}
		if(Dis[T]>1e14) break;
		else dfs(S,inf);//not flow+=dfs(S,inf) !
	}
	flow=o[ont].w;//here
	o[ont].w=o[ont-1].w=0;

第一次 Dinic 出的原始数据只是调整流量而非 s-t 流量。

然而，费用在第一次 Dinic 里面还是要算的，因为涉及到退流。

这个算法如你所见，确实很抽象。
正确性证明：。

对于上下界费用流需要再套一层上下界。

//P7173
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=204,M=90009,S=201,T=202;
const ll inf=1e15;
int n,m,s,t,ont=-1,h[N],cur[N],_T;
ll Delta[N],Dis[N],flow,cost;
bool vis[N]; queue<int> q;
struct star{int v,nxt; ll w,c;} o[M<<1];
void _add(int u,int v,ll w,ll c){
	o[++ont]={v,h[u],w,c},h[u]=ont;
}
void add(int u,int v,ll w,ll c){
	_add(u,v,w,c),_add(v,u,0,-c);
}
ll dfs(int u,ll f){
	// printf("dfs %d\n",u);
	if(u==_T) return f;
	vis[u]=1; ll tmp,sum=0;
	for(int _=cur[u],v;~_&&f>0;_=o[_].nxt){
		cur[u]=_;
		if(o[_].w>0&&Dis[v=o[_].v]==Dis[u]+o[_].c&&!vis[v])
			tmp=dfs(v,min(f,o[_].w)),o[_].w-=tmp,f-=tmp,sum+=tmp,o[_^1].w+=tmp,cost+=o[_].c*tmp;
	}
	vis[u]=0;
	return sum;
}
int main(){
	int u,v; ll w,c;
	scanf("%d%d%d%d",&n,&m,&s,&t);
	for(int i=1;i<=T;i++) h[i]=-1;
	for(int i=1;i<=m;i++){
		scanf("%d%d%lld%lld",&u,&v,&w,&c);
		if(c>=0) add(u,v,w,c);
		else Delta[u]+=w,Delta[v]-=w,add(v,u,w,-c),cost+=w*c;
	}
	for(int i=1;i<=n;i++)
		if(Delta[i]>0) add(i,T,Delta[i],0);
		else if(Delta[i]<0) add(S,i,-Delta[i],0);
	add(t,s,inf,0);
	_T=T;
	while(true){
		for(int i=0;i<=T;i++) cur[i]=h[i],vis[i]=0,Dis[i]=inf;
		q.push(S),vis[S]=1,Dis[S]=0;
		while(!q.empty()){
			u=q.front(),q.pop(),vis[u]=0;
			for(int _=h[u];~_;_=o[_].nxt)
				if(Dis[v=o[_].v]>Dis[u]+o[_].c&&o[_].w>0){
					Dis[v]=Dis[u]+o[_].c;
					if(!vis[v]) vis[v]=1,q.push(v);
				}
		}
		if(Dis[T]>1e14) break;
		else dfs(S,inf);
	}
	flow=o[ont].w;
	o[ont].w=o[ont-1].w=0;
	_T=t;
	while(true){
		for(int i=0;i<=T;i++) cur[i]=h[i],vis[i]=0,Dis[i]=inf;
		q.push(s),vis[s]=1,Dis[s]=0;
		while(!q.empty()){
			u=q.front(),q.pop(),vis[u]=0;
			for(int _=h[u];~_;_=o[_].nxt)
				if(Dis[v=o[_].v]>Dis[u]+o[_].c&&o[_].w>0){
					Dis[v]=Dis[u]+o[_].c;
					if(!vis[v]) vis[v]=1,q.push(v);
				}
		}
		// for(int i=1;i<=n;i++) printf("Dis[%d]=%lld\n",i,Dis[i]);
		if(Dis[t]>1e14) break;
		else flow+=dfs(s,inf);
	}
	printf("%lld %lld\n",flow,cost);
	return 0;
}

调试细节（For Dinic）

1. 当前弧优化要每次 BFS 清空，且采取赋值形式。
2. DFS 和 SPFA 都需要开标记数组，回溯时清空。
3. 注意前向星从 \(-1\) 开始计数。
4. 头指针设 \(-1\)。
5. 从 \(s\) 到 \(t\) 进行 BFS，每次要清空。
6. DFS 的时候传回最大流，跑费用的时候在 DFS 过程中改边权算费用。
7. 跑上下界记得删 \(t\to s\) 的边，注意 \(\Delta\) 函数计算方法，想好了再写。
8. 不要把费用和容量弄混，BFS 要检测边权大于零，DFS 也是。
9. DFS 的时候，记住要用 Distance 或 Level 进行转移。
10. SPFA 退出之后重置标记。
11. 双向建边开二倍。
12. 不卡常少用 HLPP。

例题

Simple 有源汇上下界最大流模板

形式化题意：
对于一个初始为全零的序列进行 \(n\) 次操作。
第 \(i\) 次操作要求将第 \(j\) 个数增加一个 \([L(i,j),R(i,j)]\) 区间内的数，且这次操作总增量不得超过 \(D(i)\)。
要求完成操作后第 \(i\) 个数不小于 \(G(i)\)。
最大化操作后序列和。

这和网络流有关系？
增量区间很明显的提示我们：这题是一道上下界网络流。
怎么刻画这个限制呢？
还有一个总增量的限制，大概是用边权限制。

考虑对于每次操作和每个数都建一个点。
源点向操作连边 \([0,D(i)]\)。
操作和数字间连边 \([L(i,j),R(i,j)]\)。
数字和汇点间连边 \([G(i),\infty)\)。
跑最大流即可。

注意到题面中“同一天中输入的少女编号可能有重复，此时每个限制分别对应一次独立的拍摄，应当分别满足，互不影响”。
显然直接建边即可，无需特殊处理。

#include<bits/stdc++.h>
#define Day(x) (x)
#define Num(x) (x+1+n)
#define _S (0)
#define _T (n+m+1)
#define S (n+m+2)
#define T (n+m+3)
using namespace std;
typedef int ll;
const int N=1378,M=4e5+7; const ll inf=1e9;
int n,m,h[N],ont; ll Delta[N]; struct star{int v,nxt; ll w;} o[M<<2];
inline void _Link(int u,int v,ll w){o[++ont]={v,h[u],w},h[u]=ont;}
inline void Link(int u,int v,ll b,ll c){Delta[v]-=b,Delta[u]+=b; _Link(u,v,c-b),_Link(v,u,0);}
namespace _Dinic{
	queue<int> q; int dis[N],cur[N],s,t;
	ll dfs(int u,ll f){
		ll sum=0,tmp;
		if(u==t) return f;
		for(int _=cur[u],v;~_&&f>0;_=o[_].nxt) if(o[_].w>0&&dis[u]+1==dis[v=o[_].v]){
			cur[u]=_,tmp=dfs(v,min(f,o[_].w)),sum+=tmp,o[_].w-=tmp,o[_^1].w+=tmp,f-=tmp;
		}
		return sum;
	}
	ll Dinic(int _s,int _t){
		int u; ll flow=0; s=_s,t=_t;
		while(true){
			for(int i=0;i<=T;i++) dis[i]=1e9+7,cur[i]=h[i];
			dis[s]=0,q.push(s);
			while(!q.empty()){
				u=q.front(),q.pop(); 
				for(int _=h[u],v;~_;_=o[_].nxt) if(dis[v=o[_].v]==1e9+7&&o[_].w>0) q.push(v),dis[v]=dis[u]+1;
			}
			if(dis[t]==1e9+7) return flow; else flow+=dfs(s,inf);
		}
	}
}
using _Dinic::Dinic;
int main(){
	ll x,flg,tmp; 
	while(scanf("%d%d",&n,&m)!=EOF){
		ont=-1,flg=0; for(int i=0;i<=T;i++) h[i]=-1,Delta[i]=0;
		for(int i=0;i<m;i++) scanf("%d",&x),Link(Num(i),_T,x,inf);
		for(int i=1,c,d,l,r;i<=n;i++){
			scanf("%d%d",&c,&d),Link(_S,Day(i),0,d);
			while(c--) scanf("%d%d%d",&d,&l,&r),Link(Day(i),Num(d),l,r);
		}
		for(int i=0;i<=_T;i++) if(Delta[i]>0) flg+=Delta[i],Link(i,T,0,Delta[i]); else if(Delta[i]<0) Link(S,i,0,-Delta[i]); 
		Link(_T,_S,0,inf);
		if((tmp=Dinic(S,T))<flg) puts("-1\n"); else o[ont].w=o[ont-1].w=0,printf("%d\n\n",Dinic(_S,_T)+tmp);
 	} 
	return 0;
}

Simple 二分图匹配

对于二分图匹配问题，有匈牙利算法可以 \(O(nm)\) 求解。

一个图的匹配，即对于一个图选出若干条边，使得顶点两两不重。

类似 Fold-Fulkerson 的，匈牙利算法也有其对增广路的定义。
事实上，一条由非匹配边开始，非匹配边结束，同时中间由匹配边和非匹配边交错连接的边被称作增广路。
显然，对于增广路而言，其可以通过反转每一条边使得匹配数加一。
有证明，一个二分图已经达到最大匹配当且仅当不存在增广路。

实现上：
首先染色法判定二分图。
然后依次从一部枚举每一个点。

1. 如果该点未被匹配，就进行匹配。
2. 如果该点已经被匹配，就递归尝试能否让其对应节点更换匹配，直到更换成功或找不到合法方案结束为止。

考虑 DFS 不能有环，于是使用标记数组进行处理即可。
相当于我们对于一个点找增广路，若找不到则后续节点也找不到，若在寻找中则后续节点不可使用该节点进行增广。

#include<bits/stdc++.h>
using namespace std;
const int N=1009;
vector<int> k[N];
int n,m,e,match[N]; bool vis[N];
void Link(int u,int v){match[u]=v,match[v]=u;}
bool dfs(int u){
	for(int v:k[u]) if(!vis[v]){vis[v] = true; if(match[v]==0||dfs(match[v])){Link(u,v); return 1;}}
	return 0;
}
int main(){
	scanf("%d%d%d",&n,&m,&e); int cnt=0;
	for(int i=1,u,v;i<=e;i++) scanf("%d%d",&u,&v),k[u].push_back(n+v),k[n+v].push_back(u);
	for(int i=1;i<=n;i++) if(dfs(i)) ++cnt,memset(vis,0,sizeof vis);
	printf("%d\n",cnt);
	return 0;
}

考虑网络流做法。
容易想到左部点连源点，右部点连汇点，容量设一，直接跑最大流。
由于每条边容量只有一，满流边至多对于一个顶点只有一条。
直接判满流即可，时间复杂度 \(O(\sqrt n m)\)。

#include<bits/stdc++.h>
using namespace std;
const int N=1009,M=(N * 2 + 50010),inf=60009;
struct star{int v,nxt,w;}o[M<<1]; queue<int> q;
int h[N],cur[N],dis[N],n,m,e,S,T,ont=-1; bool vis[N];
void add(int u,int v,int w){o[++ont]={v,h[u],w},h[u]=ont;}
int dfs(int u,int f){
	if(u==n+m+1) return f; vis[u]=1; int ans=0;
	for(int _=cur[u],v,tmp;~_&&f>0;_=o[_].nxt) {
		cur[u]=_;
		if(!vis[v=o[_].v]&&dis[v]==dis[u]+1&&o[_].w>0) tmp=dfs(v,min(f,o[_].w)),o[_].w-=tmp,f-=tmp,o[_^1].w+=tmp,ans+=tmp;
	}
	return ans;
}
int main(){
	int u,v,ans=0;
	scanf("%d%d%d",&n,&m,&e),S=0,T=n+m+1; for(int i=S;i<=T;i++) h[i]=-1;
	for(int i=1;i<=n;i++) add(S,i,1),add(i,S,0); for(int i=1;i<=m;i++) add(i+n,T,1),add(T,i+n,0);
	for(int i=1;i<=e;i++) scanf("%d%d",&u,&v),add(u,v+n,1),add(v+n,u,0);
	while(true){
		for(int i=S;i<=T;i++) cur[i]=h[i],dis[i]=inf,vis[i]=0;
		q.push(S),dis[S]=0,vis[S]=1;
		while(!q.empty()){u=q.front(),q.pop(); for(int _=h[u];~_;_=o[_].nxt) if(o[_].w>0&&dis[v=o[_].v]==inf) dis[v]=dis[u]+1,q.push(v);}
		if(dis[T]==inf) printf("%d\n",ans),exit(0); else ans+=dfs(S,inf);
	}
	return 0;
}

Simple 支线剧情

形式化题意：对于一个单源 DAG，要求从源点走若干条路径遍历每一条边，求最小代价。

这个题比上一个更模板。
显然要的就是一个流。
我们跑上下界最小费用可行流，
建立超级汇点连接所有汇点，
每条边设为 \([1,+\infty)\) 即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll; 
const int N=309,M=9009; const ll inf=1e14; queue<int> q; ll Dis[N],ans; bool vis[N];
int n,h[N],ont=-1,Delta[N],cur[N]; struct star{int v,nxt;ll w,c;} o[M<<1];
inline void _add(int u,int v,ll w,ll c){o[++ont]={v,h[u],w,c},h[u]=ont;}
inline void add(int u,int v,ll w,ll c){_add(u,v,w,c),_add(v,u,0,-c);}
ll dfs(int u,ll f){
	if(u==n+2) return f;
	ll sum=0; vis[u]=1;
	for(int _=cur[u],v,tmp;~_&&f>0;_=o[_].nxt){
        cur[u]=_;
		if(Dis[v=o[_].v]==Dis[u]+o[_].c&&o[_].w>0&&vis[v]==0) tmp=dfs(v,min(f,o[_].w)),sum+=tmp,f-=tmp,o[_].w-=tmp,o[_^1].w+=tmp,ans+=o[_].c*tmp;
	}
	return sum;
}
int main(){ 
    scanf("%d",&n); for(int i=0;i<=n+2;i++) h[i]=-1;
	for(int u=1,j,v,w;u<=n;u++){
		scanf("%d",&j); 
		add(u,n+1,inf,0);
		while(j--) scanf("%d%d",&v,&w),add(u,v,inf,w),ans+=w,Delta[u]++,Delta[v]--;
	}
	add(n+1,1,inf,0);
	for(int u=1;u<=n;u++) if(Delta[u]>0) add(u,n+2,Delta[u],0); else if(Delta[u]<0) add(0,u,-Delta[u],0);
	int u,v;
	while(true){
		for(int i=0;i<=n+2;i++) Dis[i]=inf,cur[i]=h[i],vis[i]=0;
		Dis[0]=0,q.push(0),vis[0]=1;
		while(!q.empty()){
			u=q.front(),q.pop(),vis[u]=0;
			for(int _=h[u];~_;_=o[_].nxt) if(o[_].w>0&&Dis[v=o[_].v]>Dis[u]+o[_].c){
				Dis[v]=Dis[u]+o[_].c; if(!vis[v]) vis[v]=1,q.push(v);
			}
		}
		if(Dis[n+2]==inf) printf("%lld\n",ans),exit(0); else dfs(0,inf); 
	}
	return 0; 
} 

Simple 修车

我们需要刻画什么？
每辆车、每个人、不同时间……

联想到第一个模板，有个自然的思路：

对于每辆车和每个人开一个点。
车人相连有其费用。
最后给车所在的边设置下界跑上下界费用流。

然而他要的是集体等待时间，
换言之，一辆车修的时候等的人不止一个。

经典 trick 01：拆点网络流。
当一个点不足以表示状态时，考虑将状态拆为多个点进行求解。

对于本题考虑将一个人拆成多个点，表示“修第 \(k\) 辆车时的人”。
然而转移困难，思考优化状态设计。
发现我们只关心还有几个人，修改状态定义为“修倒数第 \(k\) 辆车时的人”。

显然初始时我们会把车集 \(C\) 划分成每个人所修车集 \(C_1,C_2,\dots，C_n\)。
所以这样设状态可行。

考虑建图。
由源点连向每一辆车，费用 \(0\) 边权 \(1\)。
由每一辆车流向拆点后的人，费用 \(k\times f(i,j)\)。
跑朴素费用流即可，显然最大流就符合条件，不用加上下界。

#include<bits/stdc++.h>
#define S 0
#define Car(x) (x)
#define Person(x,k) (n+((k)-1)*m+(x))
#define T (n*m+m+1) 
using namespace std;
typedef long long ll; const int N=609,M=36000; const ll inf=1e14; queue<int> q; bool vis[N];
int m,n,ont=-1,h[N],mp[66][12],cur[N]; struct star{int v,nxt; ll w,c;}o[M<<1]; ll dis[N],flow,cost;
void _Link(int u,int v,ll w,ll c){o[++ont]={v,h[u],w,c},h[u]=ont;}
void Link(int u,int v,ll w,ll c){_Link(u,v,w,c),_Link(v,u,0,-c);}
ll dfs(int u,ll f){
	if(u==T) return f; ll sum=0,tmp; vis[u]=1;
	for(int _=cur[u],v;~_&&f>0;_=o[_].nxt){
		cur[u]=_;
		if(vis[v=o[_].v]==0&&dis[v=o[_].v]==dis[u]+o[_].c&&o[_].w>0) tmp=dfs(v,min(f,o[_].w)),o[_].w-=tmp,f-=tmp,sum+=tmp,o[_^1].w+=tmp,cost+=o[_].c*tmp;
	} 
	vis[u]=0; return sum;
}
int main(){
	scanf("%d%d",&m,&n); //person & car
	for(int i=0;i<=T;i++) h[i]=-1; 
	for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&mp[i][j]); //car for each person
	for(int i=1;i<=n;i++) Link(S,Car(i),1,0); for(int j=1;j<=m;j++) for(int k=1;k<=n;k++) Link(Person(j,k),T,1,0);
	for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) for(int k=1;k<=n;k++) Link(Car(i),Person(j,k),1,k*mp[i][j]);
	int u,v;
	while(true){
		for(int i=0;i<=T;i++) cur[i]=h[i],vis[i]=0,dis[i]=inf;
		q.push(S),dis[S]=0,vis[S]=1;
		while(!q.empty()){u=q.front(),q.pop(),vis[u]=0; for(int _=h[u];~_;_=o[_].nxt) if(dis[v=o[_].v]>dis[u]+o[_].c&&o[_].w>0){dis[v=o[_].v]=dis[u]+o[_].c; if(!vis[v]) vis[v]=1,q.push(v);}}
		if(dis[T]==inf) printf("%.2lf\n",(double)cost/(double)n),exit(0); else flow+=dfs(S,inf);
	}
 	return 0;
} 

Medium 新生舞会

形式化题意：
给定矩阵 \(a,b\)，要求构造两个 \(n\) 阶排列 \(m,n\)，最大化以下式子的值：

\[\frac{\sum_{i=1} a(m_i,n_i)}{\sum_{i=1} b(m_i,n_i)} \]

数据范围 \(100\)。

其实，就是这种搜索过不了，数据非常小，dp 不会写的题可以考虑网络流。
然而该式不具有可加性，设出状态怎么合并？
考虑钦定 \(n\)，变成 \(\frac{\sum_{i=1} a(m_i,i)}{\sum_{i=1} b(m_i,i)}\)。

考虑分数规划的题进行二分。

分数规划，即对于一个求和相除的式子进行求解。
example P1570

\[ans\le\frac {\sum v_i}{\sum c_i}\to\sum(c_i\times ans-v_i)\le 0 \]

显然我们想让等号取等。
这个式子实际上的含义就是判断当前解是否可行
于是我们就将这些数求出来，排序，取最小的 \(m\) 项判正负。
实数二分求解即可。

#include<bits/stdc++.h>
using namespace std;
typedef double db; const int N=209; const db eps=1e-5; db v[N],c[N],tmp[N]; int n,m;
bool check(db x){
    db sum=0;
    for(int i=1;i<=n;i++) tmp[i]=c[i]*x-v[i]; sort(tmp+1,tmp+n+1);
    for(int i=1;i<=m;i++) sum+=tmp[i];
    return (sum<0);
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1,_v;i<=n;i++) scanf("%d",&_v),v[i]=_v;
    for(int i=1,_c;i<=n;i++) scanf("%d",&_c),c[i]=_c;
    db l=0,r=20000.0,mid;
    while(r-l>eps){
        mid=(l+r)/2.0;
        if(check(mid)) l=mid; else r=mid;
    }
    printf("%.3lf",r);
    return 0;
}

套路的推式子，\(\sum b(m_i,i)\times ans-a(m_i,i)\le0\)
接下来的问题是，我们能否求出左半部分的最小值（给定 \(ans\)）？
发现一种合法的建图方式：

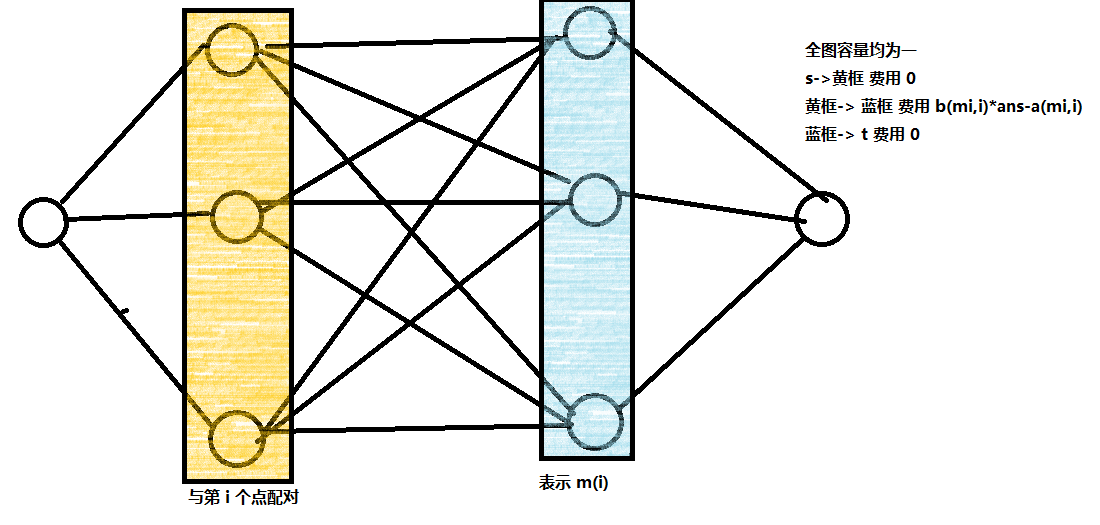
问题在于，每次二分都要重新建图，不会 TLE 吗？
考虑 \(O(\log (\frac T{eps}) n^4)\) 这不炸？
其实不会，因为这是二分图！
那大概只有 \(O(\log (\frac T{eps}) n^{\frac 5 2})\)，运算次数 \(5\times 10^6\) 可过。

注意，容量用 int，费用要 double。

#include<bits/stdc++.h>
#define S (0)
#define T (n+n+1)
using namespace std;
typedef long double db;
const db eps=1e-8,inf=1e15;
const int N=209,M=10209,INF=10000;
int ont=-1,n,h[N],cur[N]; db a[109][109],b[109][109],Dis[N],cost; queue<int> q;
struct star{int v,w,nxt; db c;} o[M<<1]; bool vis[N];
void _Link(int u,int v,int w,db c){o[++ont]={v,w,h[u],c},h[u]=ont;}
void Link(int u,int v,int w,db c){_Link(u,v,w,c),_Link(v,u,0,-c);}
db ABS(db x){return (x>0)?x:-x;}
int dfs(int u,int f){
    if(u==T) return f;
    vis[u]=1; int sum=0,tmp;
    for(int _=cur[u],v;~_;_=o[_].nxt) if(o[_].w>0&&ABS(Dis[u]+o[_].c-Dis[v=o[_].v])<1e-3&&!vis[v])
        cur[u]=_,tmp=dfs(v,min(f,o[_].w)),f-=tmp,o[_].w-=tmp,sum+=tmp,o[_^1].w+=tmp,cost+=(db)tmp*o[_].c;
    return sum;
}
bool check(db k){
    int u,v;
    ont=-1,cost=0; for(int i=S;i<=T;i++) h[i]=-1;
    for(int i=1;i<=n;i++) Link(S,i,1,0),Link(n+i,T,1,0);
    for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) Link(i,n+j,1,b[i][j]*k-a[i][j]);
    while(true){
        for(int i=S;i<=T;i++) Dis[i]=inf,vis[i]=0,cur[i]=h[i];
        q.push(S),Dis[S]=0,vis[S]=1;
        while(!q.empty()){
            u=q.front(),q.pop(),vis[u]=0;
            for(int _=h[u];~_;_=o[_].nxt) if(Dis[v=o[_].v]>Dis[u]+o[_].c&&o[_].w>0){
                Dis[v]=Dis[u]+o[_].c; if(!vis[v]) vis[v]=1,q.push(v);
            }
        }
        if(Dis[T]==inf) return (cost<0); else dfs(S,INF);
    }
}
int main(){
    int tmp; db L=0,R=1e6+5,MID; scanf("%d",&n);
    for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%d",&tmp),a[i][j]=tmp;
    for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%d",&tmp),b[i][j]=tmp;
    while(R-L>eps){
        MID=(L+R)/2.0;
        if(check(MID)) L=MID; else R=MID;
    }
   printf("%.6Lf\n",R);
}

Simple 订货

形式化题意：
有一个数 \(x\) 和 \(n\) 次操作，初始 \(x=0\)。
每次操作会给 \(x\) 加上一个数 \(k\)。
定义第 \(i\) 次操作的代价为 \(mx+kd_i\)，操作后 \(x\) 会减去 \(U_i\)，全程要求 \(x\) 非负且减去后的 \(x<S\)。
最终要求 \(x=0\)。

不需要脑子的建图显然。
由于一定可以从 inf 边获得流量，故不需要上下界，直接费用流即可。

#include<bits/stdc++.h>
#define S (0)
#define T (n+1)
using namespace std;
const int N=55,M=209,inf=1e6;
struct star{int v,nxt,w,c;} o[M<<1];
int n,m,cap,U[N],d[N],ont=-1,dis[N],cur[N],cost,h[N]; queue<int> q; bool vis[N];
inline void _Link(int u,int v,int w,int c){o[++ont]={v,h[u],w,c},h[u]=ont;}
inline void Link(int u,int v,int w,int c){_Link(u,v,w,c),_Link(v,u,0,-c);}
int dfs(int u,int f){
    if(u==T) return f; vis[u]=1; int sum=0;
    for(int _=cur[u],v,tmp;~_;_=o[_].nxt) if(o[_].w>0&&dis[v=o[_].v]==dis[u]+o[_].c&&!vis[v])
        cur[u]=_,tmp=dfs(v,min(f,o[_].w)),f-=tmp,o[_].w-=tmp,sum+=tmp,o[_^1].w+=tmp,cost+=tmp*o[_].c;
    return sum;
}
int main(){
    scanf("%d%d%d",&n,&m,&cap);
    for(int i=S;i<=T;i++) h[i]=-1;
    for(int i=1;i<=n;i++) scanf("%d",&U[i]);
    for(int i=1;i<=n;i++) scanf("%d",&d[i]);
    for(int i=1;i<=n;i++) Link(S,i,inf,d[i]),Link(i,T,U[i],0);
    for(int i=1;i<n;i++) Link(i,i+1,cap,m);
    int u,v;
    while(true){
        for(int i=S;i<=T;i++) cur[i]=h[i],dis[i]=inf,vis[i]=0;
        vis[S]=1,q.push(S),dis[S]=0;
        while(!q.empty()){
            u=q.front(),q.pop(),vis[u]=0;
            for(int _=h[u];~_;_=o[_].nxt) if(dis[v=o[_].v]>dis[u]+o[_].c&&o[_].w>0){
                dis[v]=dis[u]+o[_].c; if(!vis[v]) vis[v]=1,q.push(v);
            }
        }
        if(dis[T]==inf) printf("%d\n",cost),exit(0); else dfs(S,inf);
    }
    return 0;
}

Simple 小 M 的作物

考虑怎么刻画三个事情：选择位置，对应收益，组合收益。

最基础的限制：一种作物只能选择一块土地。
考虑用割代表不选，用权值代表其产生的惩罚。
将每种作物与源汇连边，容量分别为其收益，预先计算总收益减去最小割。
这样可以保证两者取其一。

考虑组合收益。
一个经典 trick：对于每一个组合开一个虚点。
如图：

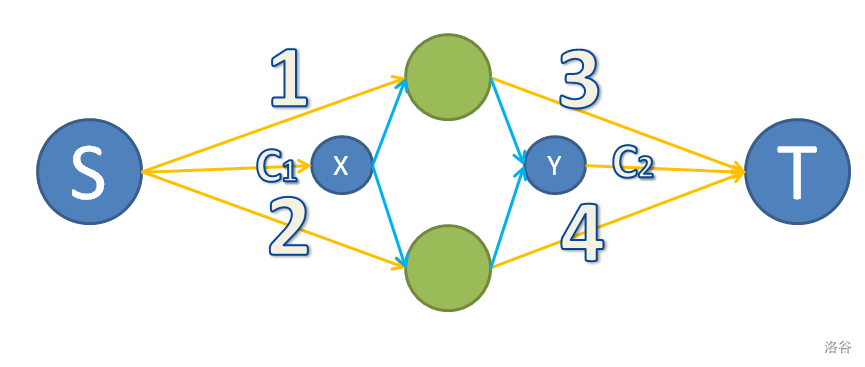
如果保留了 \(1,2\) 就可以保留 \(c_1\)。
否则一定要割掉 \(c_1\)，否则相当于所割的边没有意义。

#include<bits/stdc++.h>
#define S (0)
#define Agrp(x) (n+(x))
#define Bgrp(x) (n+m+(x))
#define T (n+m+m+1)
using namespace std;
typedef long long ll; const int N=5009,M=9e6+7,Inf=998244353; const ll inf=1e14;
struct star{int v,nxt; ll w;} o[M<<1];
int ont=-1,h[N],n,m,A[N],B[N];
void _Link(int u,int v,ll w){o[++ont]={v,h[u],w},h[u]=ont;}
void Link(int u,int v,ll w){_Link(u,v,w),_Link(v,u,0);}
namespace ISAP{
    int d[N],cur[N],gap[N],pre[N]; queue<int> q;
    bool Relable(int u){
       	cur[u]=h[u]; int tmp=T+1; for(int _=h[u];~_;_=o[_].nxt) if(o[_].w>0) tmp=min(tmp,d[o[_].v]);
        if(--gap[d[u]]==0) return 0; 
        d[u]=tmp+1,++gap[d[u]]; 
		return 1;
    }
    ll Solve(){
        int u,v; ll ans=0,tmp; for(int i=S;i<=T;i++) d[i]=Inf,cur[i]=h[i];
        d[T]=0,q.push(T);
        while(!q.empty()){
            u=q.front(),q.pop();
            for(int _=h[u];~_;_=o[_].nxt) if(d[v=o[_].v]>d[u]+1) d[v]=d[u]+1,q.push(v);
        }
        if(d[S]>1e8) return 0; for(int i=S;i<=T;i++) if(d[i]<1e8) gap[d[i]]++;
        u=S;
        while(true){
           	if(u==T){
                tmp=inf;
                for(u=T;u!=S;u=o[pre[u]^1].v) tmp=min(tmp,o[pre[u]].w);
                for(u=T;u!=S;u=o[pre[u]^1].v) o[pre[u]].w-=tmp,o[pre[u]^1].w+=tmp;
                ans+=tmp;
            }
            for(int _=cur[u];~_;_=o[_].nxt){
                cur[u]=_;
                if(o[_].w>0&&d[v=o[_].v]==d[u]-1){pre[v]=_,u=v; goto done;}
            }
            if(!Relable(u)) return ans;
            if(u!=S) u=o[pre[u]^1].v; done:;
        }
    }
}
using ISAP::Solve;
int main(){
    ll tot=0; scanf("%d",&n); memset(h,-1,sizeof h);
    for(int i=1;i<=n;i++) scanf("%d",&A[i]),tot+=A[i];
    for(int i=1;i<=n;i++) scanf("%d",&B[i]),tot+=B[i];
    scanf("%d",&m);
    for(int i=1;i<=n;i++) Link(S,i,A[i]),Link(i,T,B[i]); 
   	for(int i=1,j,_,__,___;i<=m;i++){
        scanf("%d%d%d",&j,&_,&__),tot+=_+__,Link(S,Agrp(i),_),Link(Bgrp(i),T,__);
        for(int q=1;q<=j;q++) scanf("%d",&___),Link(Agrp(i),___,inf),Link(___,Bgrp(i),inf);
    }
    printf("%lld\n",tot-Solve());
    return 0;
}

Simple 方格取数

似乎可以状压，然而 \(n\le 100\)。
注意到相邻格不能均选，考虑用最小割刻画。
考虑对于每个格子向周围四个格子连边，跑最小割。
然而直接写很难，使用黑白染色法建二分图即可。
由于特殊性质和较少的边总之能过。
注意 \(n=1\) 需要特判。

#include<bits/stdc++.h>
#define S (0)
#define T (n*m+1)
#define P(i,j) ((i-1)*m+j)
using namespace std;
typedef long long ll;
const int N=1e4+7,M=1e5+7; const ll inf=1e15;
int n,m,h[N],cur[N],dis[N],ont=-1; queue<int> q; bool vis[N];
struct star{int v,nxt; ll w;}o[M<<1];
void _Link(int u,int v,ll w){o[++ont]={v,h[u],w},h[u]=ont;}
void Link(int u,int v,ll w){_Link(u,v,w),_Link(v,u,0);}
ll dfs(int u,ll f){
	if(u==T) return f; vis[u]=1; ll sum=0,tmp;
	for(int _=cur[u],v;~_&&f>0;_=o[_].nxt) if(vis[v=o[_].v]==0&&o[_].w>0&&dis[v]==dis[u]+1)
		cur[u]=_,tmp=dfs(v,min(f,o[_].w)),o[_].w-=tmp,f-=tmp,sum+=tmp,o[_^1].w+=tmp;
	return sum;
}
int main(){
	scanf("%d%d",&n,&m); ll ans=0,sum=0;
	if(n==1&&m==1) scanf("%d",&m),printf("%d",m),exit(0);
	for(int i=S;i<=T;i++) h[i]=-1;
	for(int i=1;i<=n;i++) for(int j=1,_;j<=m;j++){
		scanf("%d",&_),sum+=_;
		if((i+j)&1){
			Link(S,P(i,j),_);
			if(i>1) Link(P(i,j),P(i-1,j),inf);
			if(j>1) Link(P(i,j),P(i,j-1),inf);
			if(i<n) Link(P(i,j),P(i+1,j),inf);
			if(j<m) Link(P(i,j),P(i,j+1),inf);
		}else{
			Link(P(i,j),T,_);
			if(i>1) Link(P(i-1,j),P(i,j),inf);
			if(j>1) Link(P(i,j-1),P(i,j),inf);
			if(i<n) Link(P(i+1,j),P(i,j),inf);
			if(j<m) Link(P(i,j+1),P(i,j),inf);
		} 
	}
	int u,v;
	while(true){
		for(int i=S;i<=T;i++) dis[i]=T+5,cur[i]=h[i],vis[i]=0;
		q.push(S),vis[S]=1,dis[S]=0;
		while(!q.empty()){
			u=q.front(),q.pop(); //printf("bfs %d\n",u);
			for(int _=h[u];~_;_=o[_].nxt) if(dis[v=o[_].v]>dis[u]+1&&o[_].w>0) dis[v]=dis[u]+1,q.push(v);			
		}
		if(dis[T]>T) printf("%lld\n",sum-ans),exit(0); else ans+=dfs(S,inf);
	}
	return 0;
}

Medium Beautiful League/石头剪刀布

题意简述：给定一个 \(n\) 个点的有向完全图，一部分边已经定向，你需要给其余边定向，构造一种方案以获得最大三元环数量。

考虑刻画“三元环”这个信息。
注意到三元环和非三元环其实只有一种形态，如图：

显然，对于一个非三元环，必定存在入度/出度为 \(0/2\) 的点。
这个性质比三元环本身要简单。

进一步思考，我们假设用“出度”作为这道网络流题目的语言。
那我们要刻画的就是三元结构中每个点只有一个出度。
因为三元结构是简单的，基础组合数学 \(C_n^3\)。

回看我们的限制：方向二选一、出度刻画，贡献求和，三元结构。
但是又有一个严重的问题：
我们的总出度和三元结构出度中间缺乏联系，
分别建点时空又不可接受。
怎么办？

人类智慧：考虑一个点出度为 \(x\)，对于其任意不重的两条出边构成的无序边对来说，其可以破坏一个三元结构使其不成为三元环。
容易证明，这种方法不会导致重复统计。

于是我们考虑这样一个问题：
我们再给所有边定向之后，最小化 \(\sum out(i)\times(out(i)-1)/2\) 的值。

研究一下一次加一操作所造成的影响。
定义 \(f(x)=\frac{x^2-x}2\)，显然有 \(f(x+1)-f(x)=\frac{x^2+2x+1-x-1-(x^2-x)}2=x\)。
这提示我们，我们的思考方向也许对了。

方向二选一？经典的二选一大概是最小割刻画。
每次操作阶梯代价？考虑拆点网络流。

这个点怎么拆呢？
显然对于一个点拆成 \(n\) 个，表示当前已经有了 \(k\) 入度的一个点。

如何刻画二选一的出度增加？怎么对拆点间的点建立联系？

先考虑第二点。
我们用流量代表出度。
发现出度为零或一实际上区别不大，可以一概而论。
由于我们推式子得到的 \(\Delta=x\)，
能够想到一种神奇的建图方式：
对于一个点 \(u\) 形成的点链 \(p(u,i)\)，考虑从 \(p(u,i)\) 到 \(p(u,i+1)\) 建一条费用为一容量 \(\inf\) 的边，
同时我们对于每个点向汇点连一条容量一费用零的边。
显然为了获得最小费用我们一定会优先走向汇点的“送流边”，能够保证我们不需要跑上下界。

第一点其实就迎刃而解了。
我们对于每条边建点，从源点来一条零费用一容量的边。
接着这个点连向两个起始点，然后就可以了。
如图所示：

只有一个问题：时间？空间？爆炸？
首先分析一下，我们 \(n\) 倍拆点，\(50\times 50=2500\)。
同时共有大概平方的边数，\(|V|\le5000\)。
同时 \(|E|\le2500\times2+2500\times3=12500\)。

显然是过不了的，思考优化。
我已经拼尽全力只能润题解了。
考虑 Dinic 的点大小是平方的。
发现我们可以把一个点拆出的点再缩回去，
从对应点向汇点连容量为一，费用依次为 \(0,1,2,3,4,5,\dots,n\) 的边。

优化后，\(|V|\le 2500\)，\(|E|\le7500\)。
按时间复杂度看还是能过我吃的题。
然而费用流，时间复杂度就是玄学无需在意，差不多就行。（图尽力了，凑合看吧）

最后的方案，上图 Link 节点看谁满流即可。

小优化：记录每个节点一共有几个入度，用一条边建好

//P4249 石头剪刀布
#include<bits/stdc++.h>
using namespace std;
typedef long long ll; const int N=5559,M=10009,inf=1e8; struct star{int v,nxt,w,c;} o[M<<1];
int n,S,T,ont=-1,h[N],cur[N],mp[N][N],tmp[N][N],dis[N],line[N][N],cost,go[N]; inline void __(int u,int v,int w,int c){o[++ont]={v,h[u],w,c},h[u]=ont;}
inline void ___(int u,int v,int w,int c){__(u,v,w,c),__(v,u,0,-c);} queue<int> q; bool vis[N]; 
int dfs(int u,int f){
	if(u==T) {vis[T]=1;return f;} vis[u]=1; int sum=0;
	for(int _=cur[u],v,tmp;~_&&f>0;_=o[_].nxt){
		cur[u]=_;
		if(!vis[v=o[_].v]&&dis[v]==dis[u]+o[_].c&&o[_].w>0) tmp=dfs(v,min(f,o[_].w)),f-=tmp,o[_].w-=tmp,sum+=tmp,o[_^1].w+=tmp,cost+=o[_].c*tmp;
	}
	vis[u]=0;
	return sum;
}
int main(){
	scanf("%d",&n),S=0; for(int i=0;i<=5500;i++) h[i]=-1; int cnt=n;
	for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){
		scanf("%d",&tmp[i][j]);
		if(i>=j) continue;
		go[i]+=(tmp[i][j]==1),go[j]+=(tmp[i][j]==0);
		if(tmp[i][j]==2) mp[i][j]=++cnt,___(S,mp[i][j],1,0),___(mp[i][j],i,1,0),line[i][j]=ont-1,___(mp[i][j],j,1,0);
	}
	T=cnt+1;
	for(int i=1;i<=n;i++) for(int j=0;j<n;j++) ___(i,T,1,j);
	for(int i=1;i<=n;i++) if(go[i]) ___(S,i,go[i],0);
	int u,v;
	while(true){
		for(int i=S;i<=T;i++) dis[i]=inf,vis[i]=0,cur[i]=h[i];
		q.push(S),vis[S]=1,dis[S]=0;
		while(!q.empty()){
			u=q.front(),q.pop(),vis[u]=0;
			for(int _=h[u];~_;_=o[_].nxt) if(o[_].w>0&&dis[v=o[_].v]>dis[u]+o[_].c){
				dis[v]=dis[u]+o[_].c; if(!vis[v]) vis[v]=1,q.push(v);
			}
		} 
		if(dis[T]==inf){
			for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){
				if(tmp[i][j]!=2) continue;
				if(i<j){
					tmp[i][j]=(o[line[i][j]].w==0)?1:0;
				}else{
					tmp[i][j]=(o[line[j][i]].w==0)?0:1;
				}
			}
			printf("%d\n",n*(n-1)*(n-2)/6-cost);
			for(int i=1;i<=n;i++){for(int j=1;j<=n;j++) printf("%d ",tmp[i][j]); putchar('\n');}
			exit(0);
		}
		else dfs(S,inf);
	}
	return 0;
}

//Beautiful League
#include<bits/stdc++.h>
using namespace std;
typedef long long ll; const int N=2559,M=90009,inf=1e8; struct star{int v,nxt,w,c;} o[M<<1];
int n,S,T,ont=-1,h[N],cur[N],mp[N][N],tmp[N][N],dis[N],line[N][N],cost,go[N]; inline void __(int u,int v,int w,int c){o[++ont]={v,h[u],w,c},h[u]=ont;}
inline void ___(int u,int v,int w,int c){__(u,v,w,c),__(v,u,0,-c);} queue<int> q; bool vis[N]; 
int dfs(int u,int f){
	if(u==T) {vis[T]=1;return f;} vis[u]=1; int sum=0;
	for(int _=cur[u],v,tmp;~_&&f>0;_=o[_].nxt){
		cur[u]=_;
		if(!vis[v=o[_].v]&&dis[v]==dis[u]+o[_].c&&o[_].w>0) tmp=dfs(v,min(f,o[_].w)),f-=tmp,o[_].w-=tmp,sum+=tmp,o[_^1].w+=tmp,cost+=o[_].c*tmp;
	}
	vis[u]=0;
	return sum;
}
int main(){
	scanf("%d",&n),S=0; for(int i=0;i<=2550;i++) h[i]=-1; int cnt=n;
	for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) tmp[i][j]=2;
	int m,l,r; scanf("%d",&m);
	while(m--) scanf("%d%d",&l,&r),tmp[l][r]=1,tmp[r][l]=0;
	for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){
		if(i>=j) continue;
		go[i]+=(tmp[i][j]==1),go[j]+=(tmp[i][j]==0);
		if(tmp[i][j]==2) mp[i][j]=++cnt,___(S,mp[i][j],1,0),___(mp[i][j],i,1,0),line[i][j]=ont-1,___(mp[i][j],j,1,0);
	}
	T=cnt+1;
	for(int i=1;i<=n;i++) for(int j=0;j<n;j++) ___(i,T,1,j);
	for(int i=1;i<=n;i++) if(go[i]) ___(S,i,go[i],0);
	int u,v;
	while(true){
		for(int i=S;i<=T;i++) dis[i]=inf,vis[i]=0,cur[i]=h[i];
		q.push(S),vis[S]=1,dis[S]=0;
		while(!q.empty()){
			u=q.front(),q.pop(),vis[u]=0;
			for(int _=h[u];~_;_=o[_].nxt) if(o[_].w>0&&dis[v=o[_].v]>dis[u]+o[_].c){
				dis[v]=dis[u]+o[_].c; if(!vis[v]) vis[v]=1,q.push(v);
			}
		} 
		if(dis[T]==inf){
			for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){
				if(tmp[i][j]!=2) continue;
				if(i<j){
					tmp[i][j]=(o[line[i][j]].w==0)?1:0;
				}else{
					tmp[i][j]=(o[line[j][i]].w==0)?0:1;
				}
			}
			for(int i=1;i<=n;i++){for(int j=1;j<=n;j++) printf("%d",tmp[i][j]); putchar('\n');}
			exit(0);
		}
		else dfs(S,inf);
	}
	return 0;
}

Medium 无限之环

考虑刻画“没有漏水处”这一限制。

Medium Snuke the Phantom Thief

首先思考一个问题：空间位置有无意义？
即，原题能否简化为如下形式：

有 \(n\) 个物品，每个物品有一个价值 \(v_i\)。
同时有 \(k\) 条限制，第 \(i\) 条限制规定一个集合 \(A_i\) 中至多可以取 \(x_i\) 个元素。
最大化所得价值。

这个问题发现直接不好做。
如果用入流或者出流去卡的话可能在相交区间会有问题。

根本问题在于，我们无法让一个点的流强制走向所有出边。
使用极大流又无法处理造成的额外流。

考虑二维空间的特殊性。

经典 trick 02：横纵坐标连边代表节点。

考虑这回能否直接卡流。
问题仍在，比如说一个模型：

n=10,m=10
坐标小于等于 3 至多选 2
坐标小于等于 5 至多选 3
坐标小于等于 6 至多选 5
坐标小于等于 9 至多选 5
坐标大于等于 3 至多选 7
坐标大于等于 6 至多选 4
坐标大于等于 7 至多选 2

假设只考虑前缀限制显然：

加上后缀限制怎么办？
考虑枚举选点数量跑上下界。
比如说我们的限制：

n=10,m=10,choose=5
坐标小于等于 3 至多选 2
坐标小于等于 5 至多选 3
坐标小于等于 6 至多选 5
坐标小于等于 9 至多选 5
坐标大于等于 3 至多选 7 -> 坐标小于等于 2 至少选 -2(0)
坐标大于等于 6 至多选 4 -> 坐标小于等于 5 至少选 1
坐标大于等于 7 至多选 2 -> 坐标小于等于 6 至少选 3

两边同时建图操作，中间连边表示选物品，连边表示费用，跑上下界最大费用可行流即可。

时间复杂度 \(O(n\sqrt{|V|}|E|)\)，其中 \(|V|\le 520,|E|\le1000,n\le80\)。

我们发现会死循环，发现是这种情况：

我们发现 \(24\to 5\to 18 \to 28\to 27\to 31\to 0\to 23 \to 24\) 是一个正环，会导致 SPFA 炸掉。
原本来说，由于网络本就允许循环，而我们只有正费用，这种情况实属在所难免。

怎么办？
码一下有负圈的费用流即可。

由于以前的代码太鬼畜了我决定全部重构。