2025/7/24
T1
对于一个矩阵 \(A_{n,m}\),求一个“口”字形区间的价值和。
形式化的说,答案为 \(\min \{A(i_1,j_1)+...+A(i_2,j_1)+A(i_1,j_2)+...+A(i_2,j_2)+A(i_1,j_1+1)+...+A(i_1,j_2-1)+A(i_2,j_1+1)+...+A(i_1,j_2-1)\}\)。
输入:第一行两个整数 \(n,m\),接下来 \(n\) 行,每行 \(m\) 个数 \(a_{i,j}\)。
输出:一个整数,即为答案。
数据范围:\(2\le n,m\le 10^5,n\times m\le 2\times 10^5,|a_{i,j}|\le 100\)。
\(O(n^2m^2)\) 做法
暴力枚举矩形,简单前缀和,期望 \(50\) 分。
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+9;
int n,m,B; vector<int> x[N],y[N];
inline int l(int i){return i*B-B+1;}
inline int r(int i,int lim){return min(lim,i*B);}
inline int ans(int la,int lb,int ra,int rb){
return x[ra][rb]-x[ra][lb-1]+y[ra-1][rb]-y[la-1][rb]+y[ra-1][lb]-y[la-1][lb]+x[la][rb-1]-x[la][lb];
}
int main(){
freopen("flower.in","r",stdin);
freopen("flower.out","w",stdout);
int answer=INT_MIN; scanf("%d%d",&n,&m);
for(int i=0;i<=n;i++) x[i].resize(m+1),y[i].resize(m+1);
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&x[i][j]),y[i][j]=x[i][j]+y[i-1][j],x[i][j]+=x[i][j-1];
for(int a=1;a<n;a++) for(int b=1;b<m;b++) for(int c=a+1;c<=n;c++) for(int d=b+1;d<=m;d++) answer=max(answer,ans(a,b,c,d));
printf("%d\n",answer);
return 0;
}
\(O(\frac{n^2m^2}{\sqrt{\max\{n,m\}}})\) 做法
暴力平方枚举较小的一维(暂写作 \(n\)),另一维分块处理。
设块长为 \(\Delta\),对于块内暴力时间复杂度 \(O(\frac m{\Delta} \Delta^2)=O(m\Delta)\);
对于块间枚举显然 \(O(\frac{m^2}{\Delta^2})\),注意到两侧互不影响,分别统计最优答案并合并,时间复杂度为 \(O(\frac{m^2}{\Delta})\)。
使用均值不等式显然 \(\Delta=\sqrt m\) 时取最小值,最终的时间复杂度为 \(O(n^2m\sqrt m)\)。
注意到 \(n,m\) 顺序并不影响答案求解,可以在输入时将 \(n\) 处理为较小值。
期望 \(50-100\) 分。
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+9;
int n,m,B; vector<int> x[N],y[N];
inline int l(int i){return i*B-B+1;}
inline int r(int i,int lim){return min(lim,i*B);}
inline int ans(int la,int lb,int ra,int rb){
if(la>=ra||lb>=rb) return 0;
return x[ra][rb]-x[ra][lb-1]+y[ra-1][rb]-y[la-1][rb]+y[ra-1][lb]-y[la-1][lb]+x[la][rb-1]-x[la][lb];
}
int main(){
freopen("flower.in","r",stdin);
freopen("flower.out","w",stdout);
int answer=INT_MIN,middle,lbest,rbest; scanf("%d%d",&n,&m);
if(n<=m){
for(int i=0;i<=n;i++) x[i].resize(m+1),y[i].resize(m+1);
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&x[i][j]),y[i][j]=x[i][j]+y[i-1][j],x[i][j]+=x[i][j-1];
}else{
for(int i=0;i<=m;i++) x[i].resize(n+1),y[i].resize(n+1);
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&x[j][i]);
swap(n,m);
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) y[i][j]=x[i][j]+y[i-1][j],x[i][j]+=x[i][j-1];
}
B=max(min((int)sqrt(m)+1,m),2);
for(int i=1;i<n;i++) for(int j=i+1;j<=n;j++){
for(int pos=1;pos<=(m+B-1)/B;pos++) for(int a=l(pos);a<r(pos,m);a++)
for(int b=a+1;b<=r(pos,m);b++) answer=max(answer,ans(i,a,j,b));
for(int lpos=1;lpos<(m+B-1)/B;lpos++) for(int rpos=lpos+1;rpos<=(m+B-1)/B;rpos++){
middle=x[i][r(rpos-1,m)]+x[j][r(rpos-1,m)]-x[i][r(lpos,m)]-x[j][r(lpos,m)]; lbest=rbest=INT_MIN;
for(int it=l(lpos);it<=r(lpos,m);it++) lbest=max(lbest,x[i][r(lpos,m)]+x[j][r(lpos,m)]-x[i][it-1]-x[j][it-1]+y[j-1][it]-y[i][it]);
for(int it=l(rpos);it<=r(rpos,m);it++) rbest=max(rbest,x[i][it]+x[j][it]-x[i][r(rpos-1,m)]-x[j][r(rpos-1,m)]+y[j-1][it]-y[i][it]);
answer=max(answer,lbest+middle+rbest);
}
}
printf("%d\n",answer);
return 0;
}
\(O(nm\min\{n,m\})\) 做法
对于较小的一维暴力枚举
设点对为 \((a,b)(c,d)\)
发现在同一式子中 \(b,d\) 不会同时出现
所以我们只需要从左到右扫一遍
迭代的过程中维护和 \(b\) 有关式子的最大信息
即可达到 \(O(nm\min\{n,m\})\)
期望 \(100\) 分。
代码
#include<bits/stdc++.h>
#define f(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
const int N=1e5+7; int n,m;
vector<int> x[N],y[N];
inline int lnum(int u,int d,int l){return y[d-1][l]-y[u][l]-x[u][l-1]-x[d][l-1];}
inline int rnum(int u,int d,int r){return x[d][r]+x[u][r]+y[d-1][r]-y[u][r];}
int main(){
freopen("flower.in","r",stdin);
freopen("flower.out","w",stdout);
bool rev=0; int tmp,ans=INT_MIN;
scanf("%d%d",&n,&m);
if(n>m) swap(n,m),rev=1;
for(int i=0;i<=n;i++) x[i].resize(m+1),y[i].resize(m+1);
if(rev) f(i,1,m) f(j,1,n) scanf("%d",&x[j][i]),y[j][i]=x[j][i];
else f(i,1,n) f(j,1,m) scanf("%d",&x[i][j]),y[i][j]=x[i][j];
f(i,1,n) f(j,1,m) x[i][j]+=x[i][j-1],y[i][j]+=y[i-1][j];
f(i,1,n-1) f(j,i+1,n){
tmp=lnum(i,j,1);
f(k,2,m) ans=max(ans,rnum(i,j,k)+tmp),tmp=max(tmp,lnum(i,j,k));
}
printf("%d\n",ans);
return 0;
}
T2
给定一个长度为 \(n\) 的序列,要求把序列划分成若干段,且每段的和都不超过 \(m\),最小化所有段最大值的和。
输入:第一行两个整数 \(n,m\),第二行 \(n\) 个整数 \(a_i\)。
输出:一个整数。
数据范围:\(1\le n\le 10^5,0\le a_i\le m\le 10^9\)
\(O(n^2)\) 做法
设 \(dp_i\) 为以 \(i\) 为结尾的最优答案,显然有转移 \(dp_i=dp_{j-1}+\max\{a_j,\dots,a_i\}(\sum_{x=j}^i a_x\le m)\)。
暴力转移,期望 \(50\) 分。
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100009;
ll a[N],dp[N];
int main(){
freopen("split.in","r",stdin);
freopen("split.out","w",stdout);
int n,m; ll sum,tmp; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%lld",&a[i]); dp[0]=0;
for(int i=1;i<=n;i++){
sum=tmp=a[i],dp[i]=LLONG_MAX;
for(int j=i-1;j>=0;j--){
dp[i]=min(dp[i],tmp+dp[j]);
sum+=a[j],tmp=max(tmp,a[j]);
if(sum>m) break;
}
}
printf("%lld\n",dp[n]);
return 0;
}
\(O(n\log n)\) 做法
用线段树优化上述转移式。
考虑在线段树中存储 \(dp\) 和 \(\max\),
那么就是单点修改和一部分的区间覆盖。
思考我们显然要维护 minsum,
那想要维护这个就需要维护 mindp 和 minmax,
同时为了判断是否能够进行覆盖还得用 maxmax。
细节很多,注意 mindp 和 minmax 不对应,无法简单相加。
期望得分 \(100\)。
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100009;
class Segment{
public:
void update(int i){
minmax[i]=min(minmax[i<<1],minmax[i<<1|1]);
mindp[i]=min(mindp[i<<1],mindp[i<<1|1]);
maxmax[i]=max(maxmax[i<<1],maxmax[i<<1|1]);
minsum[i]=min(minsum[i<<1],minsum[i<<1|1]);
}
void pushdown(int i,int l,int r){
if(tag[i]==0) return;
tag[i<<1]=tag[i<<1|1]=minmax[i<<1]=minmax[i<<1|1]=maxmax[i<<1]=maxmax[i<<1|1]=tag[i];
minsum[i<<1]=tag[i]+mindp[i<<1],minsum[i<<1|1]=tag[i]+mindp[i<<1|1];
tag[i]=0;
}
void dpmodify(int i,int l,int r,int x,ll k){
if(l==r){minsum[i]=minmax[i]+k,mindp[i]=k; return;}
int mid=(l+r)>>1; pushdown(i,l,r);
if(x<=mid) dpmodify(i<<1,l,mid,x,k); else dpmodify(i<<1|1,mid+1,r,x,k);
update(i);
}
void maxmodify(int i,int l,int r,int lim,ll k){
if(l>lim) return; if(minmax[i]>=k) return;
if(lim>=r&&maxmax[i]<=k) {minmax[i]=maxmax[i]=tag[i]=k,minsum[i]=mindp[i]+k; return;}
int mid=(l+r)>>1;
pushdown(i,l,r);
maxmodify(i<<1,l,mid,lim,k),maxmodify(i<<1|1,mid+1,r,lim,k),update(i);
}
ll query(int i,int l,int r,int L,int R){
if(l==L&&r==R) return minsum[i];
int mid=(l+r)>>1;
pushdown(i,l,r);
if(R<=mid) return query(i<<1,l,mid,L,R);
else if(L>mid) return query(i<<1|1,mid+1,r,L,R);
else return min(query(i<<1,l,mid,L,mid),query(i<<1|1,mid+1,r,mid+1,R));
}
// void dfs(int i,int l,int r){
// printf("[%d,%d] tag=%lld mindp=%lld minmax=%lld maxmax=%lld\n",l,r,tag[i],mindp[i],minmax[i],maxmax[i]);
// if(l==r) return; pushdown(i,l,r); int mid=(l+r)>>1;
// dfs(i<<1,l,mid),dfs(i<<1|1,mid+1,r);
// }
private:
ll minsum[N<<2]={},mindp[N<<2]={},minmax[N<<2]={},maxmax[N<<2]={},tag[N<<2]={};
}t;
ll a[N],sum[N],m; int n;
queue<int> q;
signed main(){
freopen("split.in","r",stdin);
freopen("split.out","w",stdout);
scanf("%d%lld",&n,&m),q.push(0);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]),sum[i]=sum[i-1]+a[i];
while(sum[i]-sum[q.front()]>m) q.pop();
t.maxmodify(1,0,n,i-1,a[i]);
// printf("from %d dp[%d]=%lld\n",q.front(),i,t.query(1,0,n,q.front(),i-1));
t.dpmodify(1,0,n,i,t.query(1,0,n,q.front(),i-1)),q.push(i);
// puts(""),t.dfs(1,0,n),puts("");
}
printf("%lld\n",t.query(1,0,n,n,n));
return 0;
}
T3
对于一颗 \(n\) 个节点以 \(1\) 为根的树,每个点上都有一个颜色为 \(0\)(白)或 \(1\)(黑)的棋子。
每次操作可以将一个棋子移除,前提是从根到它路径上没有棋子。
求移出棋子序列最小逆序对个数,其中先移除的在前。
输入:
第一行一个整数 \(n\)。
第二行 \(n-1\) 个整数,第 \(i\) 个整数表示编号为 \(i+1\) 的节点的父亲。
第三行 \(n\) 个整数,表示 \(1\) 到 \(n\) 每个点上棋子的颜色。
输出:一个整数即为答案。
数据范围:\(1\le n\le 10^5\)。
正解
对于这种操作问题,一个常规套路是考虑交换操作的影响,并形成某种偏序关系从而求解。
首先注意到一些基本性质:
- 有白必取白。
- 取黑最终必取白除非实在没有(显然从不同子树里反复取黑不优)。
- 有构造证明每次取空一个子树并不总是正确的。
由上面两条比较显然的性质,我们可以得到一个更强的性质:
感性理解,取黑的目的是为了将白解锁。
现在我们定义一段连续取完的连通块为一个 bonus,并猜测其有以下性质:
- 根为黑色
- 从当前根进行 \(dfs\) 满足前一段一直是黑,后一段一直是白
- 对于所有的“叶子”(只在
bonus中,未必是树的叶子)白节点,满足其所有儿子均为黑色
我们不再去考虑其他性质,就能看出来这是假的。
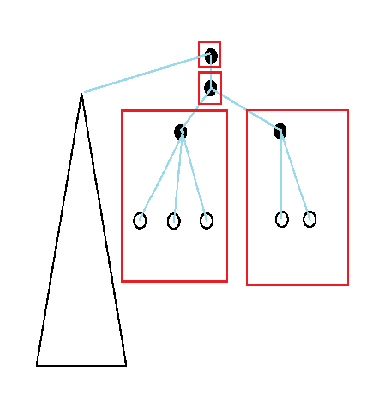
如图,按照我们刚才的定义,发现右侧应被定义为一个 bonus,
然而这并不对。
我们可能只取完一侧的白就去取另一边。
我们大概可以修正为应是一条上黑下白的链,
但你很难判断连左还是右。
那这种情况下我们修改定义:
一个 bonus 为一棵根节点为其唯一黑色节点的数上连通块。(上图一个红框就是一个 bonus)
这显然是没有问题的,现在思考接下来怎么做。
不考虑特殊情况的话,我们先考虑对于几个 bonus 的顺序。
设两个 bonus 分别有 \(w_1,w_2\) 个白色节点,\(b_1,b_2\) 个黑色节点,\(r_1,r_2\) 个逆序对。
(由于我们一会会涉及到连通块合并操作,故这几个值的确有必要)
如果一放前二放后的话,\(r_{tot}=r_1+r_2+w_1*b_1+w_2*b_2+w_2*b_1\)。
反之,\(r_{tot}'=r_1+r_2+w_2*b_2+w_1*b_1+w_1*b_2\)。
其实这个后面还应当加上已有黑色节点数*当前两块白色节点数,
但是由于两侧均要加所以就都不加了。
接下来做差法解不等式,
\(\Delta=w_2*b_1-w_1*b_2\),所以 \(r_{tot}<r_{tot}'\) 等价于 \(w_2b_1<w_1b_2\) 即 \(\frac{b_1}{w_1}<\frac{b_2}{w_2}\)。
然而,这可能没有意义。
考虑如果两个 bonus 都是纯黑那无所谓,一黑一杂显然杂色在前。
那我们就可以修改为 \(\frac{w_1}{b_1}>\frac{w_2}{b_2}\)。(bonus 显然有黑)
感性理解就是黑成分越低优先级越高。
为了便于表述我们把这个值记为 \(\alpha\)。
发现从上到下进行删除过于复杂,还会遇到等权情况,所以我们考虑使用“合并”操作。
我们每次选择 \(\alpha\) 最大值并将其合并到其父节点 bonus 中。
这表示他们作为一个连通块会被一起取到。
我们由于合并是删除的逆操作,当一个 bonus 合并到了根所在的 bonus 时就代表他被删掉了。
于是就在这时统计其对答案的贡献。
最后是实现细节。
我们有插入,删除,合并,取最小值操作。
可以写一个 FHQ-Treap,
而用并查集维护合并,
只是实现很难。
机房大佬说,可以对于每个节点维护其所在的 id。
这样在删除结点的时候如果知道编号可以直接将左右儿子搞到其父节点上。
合并的时候就先把他和父节点全部删掉,
然后再把合并好的东西插入回来。
接下来的问题是在合并的时候,
我们要注意在并查集中把当前 bonus 的 father 设为其父 bonus。
这样可以保证父 bonus 的 id 不会变。
当然我们可能需要对于 newnode 操作进行修改,
是只能该处一个指定的编号而非 ++idx。
\(\text{It's time for you to face the weather.}\)
代码



 浙公网安备 33010602011771号
浙公网安备 33010602011771号