欧拉回路
基础概念
欧拉路径:在一个图中刚好走过所有边一次的一个路径。(一笔画)
欧拉回路:起终点一致的欧拉路径。
欧拉图:具有欧拉回路的图。(能一笔画,起终点相同)
半欧拉图:具有欧拉路径的图。(能一笔画,起终点不同)
小学奥数
如果一张无向图能一笔画,那么它必然有零个或两个奇点。
他每多两个奇点就需要多加一条边
我们把他扩展一下
对于有向图
”奇点“ 指出度和入度相差一的点
入度大的是终点,出度大的是起点(显然总入度 = 总出度)
同时剩下的点入度和出度相等
如果一张图有两个奇点,那么他是半欧拉图
如果他没有奇点,那么他是欧拉图
而且还要求原图必须联通
无向图拿并查集搞一下就可以
有向图要求其 "弱联通" (就是把有向边替换成无向边后原图联通)也可以拿并查集搞
欧拉回路有向图求法
Basic Thought
首先任取一个点,DFS 找环,标记走过的边
重要性质:一直 \(dfs\) 必能找到环
一直 DFS 直到回到当前节点且所有的出边都已走过
然后在 DFS 的过程中把走过的节点加入一个数据结构
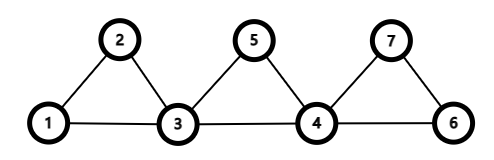
举个例子,如图
首先遍历到了 \(1\) 进行DFS
假设我们走了 \(1\to 3\to 2\to 1\)
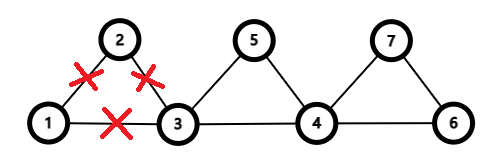
然后我们再检查这个序列
发现 \(3\) 还有出边,我们又找到了一个环 \(3\to 4\to 5\to 3\)
那就用他来替换掉原来的那个 \(3\)
序列变为 \(1\to 3\to 4\to 5\to 3\to 2\to 1\)
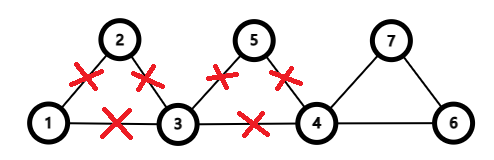
再次检查序列,\(4\) 还有出边
最终序列 \(1\to 3\to 4\to 6\to 7\to 4\to 5\to 3\to 2\to 1\)
注意我们找环的时候是要找到起始节点没有剩余出边而非回到起始节点!
Special DFS
我们实现的时候有一个更简单的方式
vector<line> ans;
void dfs(int i){
for(line j:k[i]){
if(marked(j)) continue;
mark_line(j);
dfs(j.to);
ans.push_back(make_line(i,j));
}
}
我们在回溯的时候把答案加入 \(vector\) 里
最后再倒过来就是原来的欧拉回路了
因为这种方式到一个点我们就会便历其所有的路径
不需要进行恶心的插入了
以上面的图为例给一段数据
id=1 goto 3
id=3 goto 2
id=2 goto 1
id=1 failed goto
id=2 insert (2,1)
id=3 insert (3,2)
id=3 goto 4
id=4 goto 5
id=5 goto 3
id=3 failed goto
id=5 insert (5,3)
id=4 insert (4,5)
id=4 goto 6
id=6 goto 7
id=7 goto 4
id=4 failed goto
id=7 insert(7,4)
id=6 insert(6,7)
id=4 insert(4.6)
id=3 insert(3,4)
id=1 insert(1,3)
vector: (2,1) (3,2) (5,3) (4,5) (7,4) (6,7) (4,6) (3,4) (1,3)
reverse ans: 1 3 4 6 7 4 5 3 2 1
QwQ
欧拉路径有向图求法
欧拉路径求法相同
只是起点固定
对于无向图
开始蒟蒻作者
这不把一条无向边拆成两条有向边当有向图做就可以吗
显然不行
因为一条无向边只能走一次
所以我们 \(DFS\) 的时候要删两条边
我们可以用链式前向星来存图
然后每条边的反边就是 \(x\oplus1\) \(\text{(0-index)}\)
int head[N],cnt=-1;//0-index
struct star{int to,nxt;bool mark;}k[M];
void _add(int l,int r){k[++cnt]={r,head[l],0},head[l]=cnt;}
void add(int l,r){_add(l,r),_add(r,l);}
void dfs(int i){
for(int it=head[i];it;it=k[it].nxt){
if(k[it].mark) continue;
k[it].mark=k[it^1].mark=1;
dfs(j.to);
ans.push_back(make_line(i,j));
}
}
优化
只有一个字符
把遍历字符 \(it\) 传作 \(head\) 的引用
每次遍历时更新 \(head\) 的值
因为遍历过的必然没有没用了
这样效率能快很多
但有一个问题:\(head[x]\) 很容易在更新的过程中被修改,进而把 \(i\) 的值也改掉
所以需要开一个 \(tmp[i]\) 记录其位置
//vector mode
int np[N],size[N];
vector<int> k[N];
void dfs(int x){
for(int &i=np[x],tmpi;i<size[x];i++) ...
}
//star mode
int head[N];
struct star{int to,nxt;}k[N];
void dfs(int x){
for(int &i=head[x],tmpi;~i;i=k[i].nxt) ...
}
模板 Code
思考一个问题:字典序最小怎么搞?
我们如果用 \(vector\) 存储很方便
直接排一下序
但无向图仅支持前向星
那我们就只能先开一个辅助邻接表进行排序
搞好了再插回前向星里
又由于这题恶心的要求输入边的编号
我们就只能在邻接表和前向星里都搞一个编号
然后在 \(DFS\) 的时候带着
注意由于前向星 \(\text{0-index}\) 我们就必须将 \(head\) 设为初始 \(-1\)
但到此并未结束
我们发现他这时候就不满足前面反边的性质了
我们不得不在开一个哈希表来记录每一条边的 \(\text{id}\)
然后再搞
而且此题要求走过所有边
要判掉孤立点
#include<cstdio>
#include<vector>
#include<unordered_map>
#include<cstdlib>
#include<algorithm>
using std::vector;
using std::unordered_map;
using std::max;
const int N=100002,K=400002;
int n,m,head[N],cnt=-1,ans[K],top;
struct star{int to,nxt,id,marked;} k[K];
namespace merge_set{
int fa[N];
void memset(){for(int i=1;i<=n;i++) fa[i]=i;}
int F(int x){return (x==fa[x])?x:fa[x]=F(fa[x]);}
void M(int x,int y){x=F(x),y=F(y),fa[x]=y;}
bool check(){
int base=0;
for(int i=1;i<=n;i++) fa[i]=F(i);
for(int i=1;i<=n;i++) if(head[i]!=-1) base=fa[i];
for(int i=1;i<=n;i++) if(fa[i]!=base&&head[i]!=-1) return 0;
return 1;
}
}
namespace double_edge{
using namespace merge_set;
int in[N];
struct node{int to,id;};
vector<node> tmp[N];
unordered_map<int,int> mp;
bool cmp(node a,node b){return a.to>b.to;} //反向排序逆序插入
void add(int l,int r,int id){k[++cnt]={r,head[l],id,0},head[l]=mp[id]=cnt,++in[r];}
void dfs(int x){
for(int &i=head[x],tmpi;~i;i=k[i].nxt){
if(k[i].marked)continue;
k[i].marked=k[mp[-k[i].id]].marked=1,tmpi=i;
//printf("id=%d goto %d\n",x,k[i].to);
dfs(k[i].to),ans[++top]=k[tmpi].id;
//printf("add %d->%d %d\n",x,k[i].to,k[i].id);
}
}
void solve(){
int l,r;
memset();
for(int i=1;i<=m;i++) scanf("%d%d",&l,&r),tmp[l].push_back({r,i}),tmp[r].push_back({l,-i}),M(l,r);
for(int i=1;i<=n;i++){
sort(tmp[i].begin(),tmp[i].end(),cmp);
for(node j:tmp[i]) add(i,j.to,j.id);
}
for(int i=1;i<=n;i++) if(in[i]&1) puts("NO"),exit(0);
if(!check()) puts("NO"),exit(0);
puts("YES");
for(int i=1;i<=n;i++) if(~head[i]){dfs(i);break;}
}
}
namespace single_edge{
using namespace merge_set;
int in[N],out[N];
struct node{int to,id;};
vector<node> tmp[N];
bool cmp(node a,node b){return a.to>b.to;}
void add(int l,int r,int id){k[++cnt]={r,head[l],id,0},head[l]=cnt,++in[r],++out[l];}
void dfs(int x){
for(int &i=head[x],tmpi;~i;i=k[i].nxt){
// printf("head[%d] -> %d\n",x,k[i].to);
if(k[i].marked)continue; k[i].marked=1,tmpi=i;
//printf("id=%d goto %d\n",x,k[i].to);
dfs(k[i].to),ans[++top]=k[tmpi].id;
//printf("add %d->%d %d\n",x,k[i].to,k[i].id);
}
}
void solve(){
int l,r; memset();
for(int i=1;i<=m;i++) scanf("%d%d",&l,&r),tmp[l].push_back({r,i}),M(l,r);
for(int i=1;i<=n;i++){
sort(tmp[i].begin(),tmp[i].end(),cmp);
for(node j:tmp[i]) add(i,j.to,j.id);
}
for(int i=1;i<=n;i++) if(in[i]!=out[i]) puts("NO"),exit(0);
if(!check()) puts("NO"),exit(0);
puts("YES");
for(int i=1;i<=n;i++) if(~head[i]){dfs(i);break;}
}
}
int main(){
int type;
scanf("%d%d%d",&type,&n,&m); for(int i=1;i<=n;i++) head[i]=-1;
if(type==1) double_edge::solve(); else single_edge::solve();
for(int i=top;i>=1;i--) printf("%d ",ans[i]);
return 0;
}
Sample Problem
LibreOJ 10106. 单词游戏
直接图论建模
把单词变成连结字母的边
接下来直接欧拉通路板子
#include<bits/stdc++.h>
#define yes puts("Ordering is possible.")
#define no puts("The door cannot be opened.")
using namespace std;
const int N=26;
int in[N],out[N],fa[N];
int F(int i){return (fa[i]==i)?i:fa[i]=F(fa[i]);}
int main(){
int T,n,len,base=-1,cnt;
scanf("%d",&T);
while(T--){
for(int i=0;i<26;i++)fa[i]=i;
scanf("%d",&n),memset(in,0,sizeof in),memset(out,0,sizeof out),cnt=0;
while(n--)scanf("%s",op),len=strlen(op),fa[F(op[0]-'a')]=F(op[len-1]-'a'),++out[op[0]-'a'],++in[op[len-1]-'a'];
for(int i=0;i<26;i++){
fa[i]=F(fa[i]);
if(in[i]+out[i]>0)base=fa[i];
if(in[i]==out[i]) continue;
if(abs(in[i]-out[i])>1){no;goto kill;}
++cnt;
}
if(cnt>2){no;goto kill;}
for(int i=1;i<=n;i++)if(in[i]+out[i]>0&&F(i)!=base){no;goto kill;}
yes;
kill:;
}
return 0;
}
ACP2139. 一本通欧拉回路1
板子
#include<bits/stdc++.h>
using namespace std;
const int N=1009;
int in[N],fa[N];
int F(int i){return (i==fa[i])?i:fa[i]=F(fa[i]);}
int main(){
int n,m,base,l,r;
while(true){
scanf("%d",&n),memset(in,0,sizeof in);
for(int i=1;i<=n;i++)fa[i]=i;
if(n==0)return 0;
scanf("%d",&m);
while(m--)scanf("%d%d",&l,&r),++in[l],++in[r],fa[F(l)]=F(r);
for(int i=1;i<=n;i++){
if(in[i]&1){puts("0");goto here;}
fa[i]=F(fa[i]);
if(in[i]!=0)base=fa[i];
}
for(int i=1;i<=n;i++) if(in[i]!=0&&base!=fa[i]) {puts("0");goto here;}
puts("1");
here:;
}
return 0;
}
LibreOJ 10108. Ant Trip
小学奥数结论
需要考虑联通的问题
#include<bits/stdc++.h>
using namespace std;
const int N=1009;
int in[N],fa[N],even[N],odd[N];
int F(int i){return (i==fa[i])?i:fa[i]=F(fa[i]);}
int main(){
int n,m,ans,l,r;
while(scanf("%d%d",&n,&m)){
memset(in,0,sizeof in),memset(even,0,sizeof even),memset(odd,0,sizeof odd),ans=0;
for(int i=1;i<=n;i++)fa[i]=i;
while(m--)scanf("%d%d",&l,&r),++in[l],++in[r],fa[F(l)]=F(r);
for(int i=1;i<=n;i++) if(in[i]&1) ++even[F(i)]; else if(in[i]!=0) ++odd[F(i)];
for(int i=1;i<=n;i++) if(even[i]) ans+=even[i]>>2; else if(odd[i]) ans++;
printf("%d",ans);
}
return 0;
}
LibreOJ 10109. John's Trip
模板
#include<bits/stdc++.h>
using namespace std;
const int N=80,n=50,M=5000;
int in[N],fa[N],head[N],cnt=-1;
struct star{int to,nxt,id;bool flg;} k[M];
stack<int> ans;
void add(int x,int y,int z){k[++cnt]={y,head[x],z,0},head[x]=cnt;}
int F(int i){return (i==fa[i])?i:fa[i]=F(fa[i]);}
void dfs(int x){
for(int i=head[x],ti;~i;i=k[i].nxt){
if(!k[i].flg)k[i].flg=k[i^1].flg=1,ti=i,dfs(k[i].to),ans.push(k[ti].id);
if(i==-1)break;
}
}
int main(){
int x,y,z,start,base;
while(true){
cnt=-1; for(int i=1;i<=n;i++) fa[i]=i,in[i]=0,head[i]=-1;
scanf("%d%d",&x,&y),start=min(x,y); if(x==0) return 0; scanf("%d",&z),add(x,y,z),add(y,x,z),++in[x],++in[y],fa[F(x)]=F(y);
while(true){scanf("%d%d",&x,&y); if(x==0&&y==0) break; scanf("%d",&z),add(x,y,z),add(y,x,z),++in[x],++in[y],fa[F(x)]=F(y);}
for(int i=1;i<=n;i++){
if(in[i]&1){printf("Round trip does not exist.");goto here;}
fa[i]=F(i); if(in[i]!=0) base=fa[i];
}
for(int i=1;i<=n;i++) if((in[i]&1)!=0&&fa[i]!=base){printf("Round trip does not exist.");goto here;}
dfs(start);
if(!ans.empty()) printf("%d",ans.top()),ans.pop();
while(!ans.empty()) printf(" %d",ans.top()),ans.pop();
here: putchar('\n');
}
return 0;
}
P10950 太鼓达人
考虑暴力搜索
根据玄学 \(m=2^n\)
#include<bits/stdc++.h>
using namespace std;
bool ans[10009],st[10009];
int len,go;
void dfs(int i,int j){
if(i>len){for(int it=1;it<=len;it++)printf("%d",ans[it]);exit(0);}
if(!st[j<<1]) st[j<<1]=1,dfs(i+1,(j<<1)&go);
ans[i]=1;
if(!st[j<<1|1]) st[j<<1|1]=1,dfs(i+1,(j<<1|1)&go);
ans[i]=0;
}
int main(){
int k;
scanf("%d",&k),len=1<<k,go=(len-1)>>1,st[0]=1;
printf("%d ",len);
dfs(k+1,0);
return 0;
}
LibreOJ 10111. 相框
本题场切的绝对是神犇
思维难度至少紫
然而和欧拉回路没有任何关系
更换概念&明确题意
我们假设一个熔点可以分成多个
一次操作后该熔点可分成许多熔点分别连接一些线段
同时发现题意是两个线段如果有两端上都有熔点那么他们也可以一次融合
所以我们可以给每一个自由点向下开一个新的编号
作为新点加入探究
分类讨论
- 如果全图只有一个连通块,那么我们要把它变成环
那对于一个度大于 \(2\) 的点显然要熔一次
接下来维护奇点,显然这些至少两个要融一次 - 如果全图有很多连通块,我们就要把他们变成链后再用 \(cnt\) 次进行融合
思路伪代码
graph t;
read(t);
k=t.find_block();
single=t.find_single();
multi=t.find_multi();
if(k==1) ans=multi+single/2;
else{
for(block)
each=...;
ans=sum(each)+k;
}
print(ans);
Code
#include<bits/stdc++.h>
using namespace std;
const int N=101009;
int n,m,k,ans,in[N],f[N],multi[N],single[N];
int F(int i){return (i==f[i])?i:f[i]=F(f[i]);}
bool st[N];
int main(){
int l,r;
scanf("%d%d",&n,&m);
for(int i=1;i<=101000;i++) f[i]=i;
for(int i=1;i<=m;i++){
scanf("%d%d",&l,&r);
// if(l!=0||r!=0)printf("%d %d\n",l,r);
if(l==0)l=++n;
if(r==0)r=++n;
++in[l],++in[r],f[F(l)]=F(r);
}
for(int i=1;i<=n;i++){
if(in[i]==0)continue;
f[i]=F(i);
if(!st[f[i]]) st[f[i]]=1,++k;
if(in[i]>2) ++multi[f[i]];
if(in[i]&1) ++single[f[i]];
}
if(k==1){
int base;
for(int i=1;i<=n;i++) if(in[i]!=1){base=f[i];break;}
printf("%d\n",(single[base]>>1)+multi[base]);
}else{
for(int i=1,each,m,s;i<=n;i++){
if(!st[i])continue;
m=multi[i],s=single[i];
if(m==0&&s==0) each=1;
else if(m==0&&s!=0) each=(s-2)>>1;
else if(m!=0&&s==0) each=m;
else each=m+((s-2)>>1);
ans+=each;
}
printf("%d\n",ans+k);
}
return 0;
}
P5921 原始生物
首先思考建边
然后他其实是让你找一条欧拉路径经过所有的边
由于所有的边都会经过,只需思考还需要加入几条边使原图有欧拉路径
那么我们可以用并查集搞每个连通块的信息
然后处理联通块中的所有点入度与出度之差的绝对值之和
然后每新建一条边就会减少二
我们减到二然后用 \(k-1\) 条边连起来即可
算小学奥数 \(\text{plus}\)
#include<bits/stdc++.h>
using namespace std;
const int n=1000,M=1024;
int fa[M],In[M],Out[M],eps[M],ans;
bool st[M][M],a[M];
int f(int i){return (i==fa[i])?i:fa[i]=f(fa[i]);}
int main(){
int T,l,r; scanf("%d",&T),ans=T; for(int i=1;i<=n;i++) fa[i]=i;
while(T--) scanf("%d%d",&l,&r),(st[l][r])?--ans:++Out[l],++In[r],fa[f(l)]=f(r);
for(int i=1;i<=n;i++){
if(In[i]+Out[i]==0)continue;
fa[i]=f(fa[i]),eps[fa[i]]+=abs(In[i]-Out[i]),a[fa[i]]=1,++ans;
}
for(int i=1;i<=n;i++) if(a[i]) ans+=min(0,(eps[i]-2)>>1);
printf("%d\n",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号