Tarjan 双连通分量基础
前置知识:\(\text{Tarjan}\) 求 \(\text{SCC}\)
概念
强连通分量,简称 \(\text{SCC}\),是指一个有向图中的一些点组成的子图任意两点之间可达
同时这个子图再加上任意一个点都不满足该性质(即所谓“极大的”)
求法
基于 \(Tarjan\) 算法
需要用两个数组 \(dfn\) 和 \(low\)
我们直接 \(\text{dfs}\) 得到了 DFS 序
同时记录一个 \(low\) 代表其能够到达的最小编号
如果我们发现从一个点开始其能到达的最小编号点即为其本身
那么说明他下面的一个东西就是一个玄学的类似环的东西(走了一坨回到自己)
于是我们搞一个栈来存点
根据玄学性质
强连通分量的 \(\text{dfn}\) 应当是连续的
然后弹栈即可
具体见 here(这个写的非常有实力)
概念介绍
双连通分量有两种,点双和边双
注意:点双和边双都是在无向图的基础上搞的!
点双连通分量
就是一个图如果删去任意一个点及其连边后
这张图不会变成多张图
那么他就是一个点双连通分量
边双连通分量也类似
只不过是一个图删去一条边后
不会变成多张图
那他就是一个边双
其实他和强连通分量是相似的
都是要求不能再扩大的一个子图
而相反的
如果一个图删去一个点就会变成多张图
则这个点就是原图的割点
如果一个图删去一个边就会变成多张图
则这个点就是原图的割边,也叫做桥
点双连通分量求法
割点求法
首先要说明
割点的求法和 \(\text{Tarjan}\) 求 \(\text{SCC}\) 是有很多共同之处的
还记得我们的 \(\text{dfn}\) 和 \(\text{low}\) 数组吗
我们仍然要用到他们
我们判断一个点是割点的依据就是
对于一个点 \(u\)
我们向下找到一条树边 \((u,v)\)
那么当 \(low[v]>=dfn[u]\)
这说明什么?
这说明如果这个节点不经过 \(u\) 的话
那么他就无法回到 \(u\) 的上面
那么 \(u\) 就是割点
式子和原来的有一些区别
因为当我们从一个点进行 \(DFS\) 发现一个点也在树里时
我们原来有两种等价的写法
low[i]=min(low[i],dfn[j]);
low[i]=min(low[i],low[j]);
但在求解割点的时候
只有上面一种方式是合法的
为什么呢?
如图
红色边就是树边
黑色边就是非树边
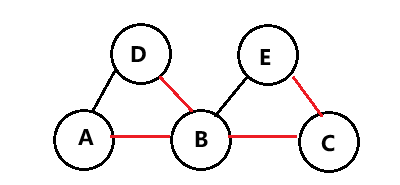
我们的 \(\text{DFS}\) 序假设为 \(\text{ABDCE}\)
那么我们先搜到了 \(D\)
把 \(\text{low[B]}\) 和 \(\text{low[D]}\) 更新成了 \(1\)
然后当你如果来到 \(E\)
用了我们第二个转移
会发生什么呢?
你会发现 \(low[D]=low[E]=1\)
但这其实不对
因为这条路径是要经过我们当前节点 \(B\) 的
并不能再删掉 \(B\) 点后实际进行回溯
如果这么判定的话就会发现 \(B\) 不是割点
出现错误
还有一个 \(bug\)
因为我们最小节点编号就是根
所以无论怎么搞 \(low\) 她都会被判成割点
但实际上当且仅当它有至少两个连接的树边时他才会变成割点
这个很简单
特判一下就好了
由于是无向图,有边必达,所以不用向求 \(\text{SCC}\) 时那样判是否走过了。但由于有判重的风险,需要 unique 一下
Code P3388
#include<bits/stdc++.h>
using namespace std;
const int N=20009;
vector<int> k[N],ans;
int n,m,idx,dfn[N],low[N];
void dfs(int i,int f){
int son=0;
dfn[i]=low[i]=++idx;
for(int j:k[i]){
if(!dfn[j]){
++son;
dfs(j,i),low[i]=min(low[i],low[j]);
if(low[j]>=dfn[i]&&f!=0)ans.push_back(i);
}else low[i]=min(low[i],dfn[j]);
}
if(f==0&&son>1)ans.push_back(i);
}
int main(){
int l,r;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++) scanf("%d%d",&l,&r),k[l].push_back(r),k[r].push_back(l);
for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i,0);
sort(ans.begin(),ans.end());
int len=unique(ans.begin(),ans.end())-ans.begin();
printf("%d\n",len);
for(int i=0;i<len;i++)printf("%d ",ans[i]);
return 0;
}
点双求法
有两个重要的性质
- 两个点双至多只有一个公共点
- 这个点必然是割点
性质简单就不证了
然后我们就会发现
一个点双里 \(dfn\) 最小的点必然是树根或者割点
然后我们搞一个栈
如果检测到当前是割点就弹栈
然后注意不要把树根和割点弹出去
因为他们还是有可能当其他的 \(BCC\) 的节点的
\(Tarjan\) 最后一行是判孤立点的特殊情况
Code P8435
#include<bits/stdc++.h>
using namespace std;
const int N=500009;
vector<int> k[N],ans[N];
stack<int> st;
int n,m,idx,dfn[N],low[N],bccnt;
void dfs(int i,int f){
int son=0;
dfn[i]=low[i]=++idx,st.push(i);
for(int j:k[i]){
if(!dfn[j]){
++son;
dfs(j,i),low[i]=min(low[i],low[j]);
//如果树根有两个以上儿子那么它是割点
//如果它只有一个那么他是对的
if(low[j]>=dfn[i]){
++bccnt;
int tmp=st.top();
//清空子树
//因为当前的割点可能在一个 BCC 里面,直接整可能 POP 了原来的 SCC
while(tmp!=j) ans[bccnt].push_back(tmp),st.pop(),tmp=st.top();
ans[bccnt].push_back(j),st.pop();//加入树根
ans[bccnt].push_back(i);//把割点也搞进去
}
}else low[i]=min(low[i],dfn[j]);
}
if(f==0&&son==0)ans[++bccnt].push_back(i);//孤立点
}
int main(){
int l,r;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++) scanf("%d%d",&l,&r),k[l].push_back(r),k[r].push_back(l);
for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i,0);
printf("%d\n",bccnt);
for(int i=1;i<=bccnt;i++){
printf("%d ",ans[i].size());
for(int j:ans[i])printf("%d ",j);
putchar('\n');
}
return 0;
}
边双连通分量求法
桥的求法
类似的,可以想到 \(low[v]>dfn[u]\) 时 \((u,v)\) 就是一条割边(具体是方括号还是圆括号我也不知道,反正是无向边)
同理 \(low\) 求法同点双
注意这个由于要求严格小于那就必须判掉返回 \(\text{father}\) 的边了
但这里就有问题
他可能有重边,这种情况下他就不能当作桥边处理
所以我们判父亲的时候要判边而非点
边双求法
那边双连通分量之间会有重复吗
显然没有
而且点双是可能有割点的
但是边双不会有桥
我们可以用并查集来搞,每次进行 \(\text{merge}\) 操作
也可以直接断掉对应的桥然后跑连通块
Code P8436
#include<bits/stdc++.h>
using namespace std;
const int N=500009;
int n,m,cnt,sccnt,dfn[N],low[N],fa[N],vis[N];
struct node{int v,idx;};
vector<node> k[N];
vector<int> ans[N];
int F(int i){return (i==fa[i])?i:fa[i]=F(fa[i]);}
void dfs(int i,int f){
dfn[i]=low[i]=++cnt;
for(node j:k[i]){
if(j.idx==f) continue;
if(!dfn[j.v]){
dfs(j.v,j.idx),low[i]=min(low[i],low[j.v]);
if(low[j.v]<=dfn[i]) fa[F(j.v)]=F(i);
}else low[i]=min(low[i],dfn[j.v]);
}
}
int main(){
int l,r;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=m;i++)scanf("%d%d",&l,&r),k[l].push_back({r,i}),k[r].push_back({l,i});
for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i,-1);
for(int it=1,i;it<=n;it++){
i=F(it);
if(vis[i]==0) vis[i]=++sccnt;
ans[vis[i]].push_back(it);
}
printf("%d\n",sccnt);
for(int i=1;i<=sccnt;i++){
printf("%d ",ans[i].size());
for(int j:ans[i])printf("%d ",j);
putchar('\n');
}
return 0;
}
Sample Problem
P2860 Redundant Paths G
这题边双 \(\text{Tarjan}\) 缩点建桥树是显然的
然后问题转化成了最少建几条边能保证任意一个点都至少在一个环上
我们想象把这颗树做成类似菊花图的样子
然后将叶子两两配对
然后你容易看出他的答案是 \(\frac{\lceil leaf\rceil}2\)
需要特判根节点是否出度为一
注意给定的图联通
需要特判整张图是一个边双的情况
#include<bits/stdc++.h>
using namespace std;
const int N=5009,M=10004;
int n,m,bcnt,sccnt,idx,dfn[N],low[N],fa[N],vis[N],leaf,col[N];
struct node{int i,j;}b[M];
vector<node> k[N];
vector<int> mp[N];
int F(int i){return (i==fa[i])?i:fa[i]=F(fa[i]);}
void dfs(int i=1,int f=-1){
dfn[i]=low[i]=++idx;
for(node j:k[i]){
if(!dfn[j.i]){
dfs(j.i,j.j),low[i]=min(low[i],low[j.i]);
if(low[j.i]>dfn[i]) b[++bcnt]={i,j.i}; else fa[F(j.i)]=F(i);
}else if(j.j!=f) low[i]=min(low[i],dfn[j.i]);
}
}
void dfs2(int i=1,int f=0){
if(mp[i].size()==1)++leaf;
for(int j:mp[i]) if(j!=f) dfs2(j,i);
}
int main(){
int l,r;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=m;i++)scanf("%d%d",&l,&r),k[l].push_back({r,i}),k[r].push_back({l,i});
dfs();
for(int i=1;i<=n;i++){
fa[i]=F(i);
if(!vis[fa[i]])vis[fa[i]]=++sccnt;
col[i]=vis[fa[i]];
}
for(int i=1;i<=bcnt;i++) if(col[b[i].i]!=col[b[i].j])
mp[col[b[i].i]].push_back(col[b[i].j]),mp[col[b[i].j]].push_back(col[b[i].i]);
dfs2();
printf("%d\n",(leaf+1)>>1);
return 0;
}
P3225 矿场搭建
本题实际难度有紫
这题首先应当是点双 \(\text{Tarjan}\) 缩点
然后分类讨论
如果一个联通块有 \(2\) 个以上割点
那他一定是断不掉的就不用建了
如果它只有一个显然不会在割点上建
我们只搞一个就够
即使这个炸了也可以走割点到其他 \(\text{BCC}\)
如果他上面没有割点那就建两个
一个炸了还有一个
至于组合数就很简单了
本题显然没有孤立点,无需考虑
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int N=505;
int dfn[N],low[N],sccnt,idx;
bool Cut[N];
vector<int> k[N],ans[N];
stack<int> st;
void dfs(int i=1){
int son=0;
dfn[i]=low[i]=++idx,st.push(i);
for(int j:k[i]){
if(!dfn[j]){
++son;
dfs(j),low[i]=min(low[i],low[j]);
if(low[j]>=dfn[i]){
Cut[i]=1,++sccnt;
while(st.top()!=j) ans[sccnt].push_back(st.top()),st.pop();
st.pop(),ans[sccnt].push_back(j),ans[sccnt].push_back(i);
}
}else low[i]=min(low[i],dfn[j]);
}
if(i==1&&son<2) Cut[i]=0;
}
ull ans1,ans2;
int main(){
int m,l,r,Case=0;
while(true){
scanf("%d",&m),++Case; if(!m) return 0;
memset(dfn,0,sizeof dfn),memset(low,0,sizeof low),memset(Cut,0,sizeof Cut),sccnt=idx=0,ans1=0,ans2=1;
while(!st.empty())st.pop();
for(int i=1;i<=501;i++) k[i].clear(),ans[i].clear();
while(m--) scanf("%d%d",&l,&r),k[l].push_back(r),k[r].push_back(l);
dfs();
for(int i=1,num=0;i<=sccnt;i++,num=0){
for(int j:ans[i]) if(Cut[j]) ++num;
if(num==0) ans1+=2,ans2*=((ans[i].size()-1)*ans[i].size())>>1;
else if(num==1) ans1++,ans2*=ans[i].size()-1;
}
printf("Case %d: %llu %llu\n",Case,ans1,ans2);
}
}
LibreOJ 10100. 网络
模板题
输入恶心
#include<bits/stdc++.h>
using namespace std;
const int N=109;
vector<int> k[N];
int sccnt,idx,low[N],dfn[N],ans,n;
bool st[N],Cut[N];
void dfs(int i,int f){
int son=0;
low[i]=dfn[i]=++idx;
for(int j:k[i]) if(!dfn[j]) dfs(j,1),low[i]=min(low[i],low[j]),++son,Cut[i]|=(low[j]>=dfn[i]); else low[i]=min(low[i],dfn[j]);
if(f==0&&son<2) Cut[i]=0;
}
int main(){
int l,tmp;
char o;
while(true){
scanf("%d",&n); if(!n) return 0;
while(true){
scanf("%d",&l),st[l]=1; if(!l)break;
o=getchar(),tmp=0;
while(o==' '||isdigit(o)){
if(!isdigit(o)){
if(tmp) k[l].push_back(tmp),k[tmp].push_back(l);
st[tmp]=1,tmp=0,o=getchar();
continue;
}
tmp=tmp*10+o-'0',o=getchar();
}
if(tmp) k[l].push_back(tmp),k[tmp].push_back(l),st[tmp]=1;
}
for(int i=1;i<=n;i++) if(dfn[i]==0&&st[i]==true) dfs(i,0);
for(int i=1;i<=n;i++) if(Cut[i]) ++ans;
printf("%d\n",ans);
memset(low,0,sizeof low),memset(dfn,0,sizeof dfn),memset(st,0,sizeof st),memset(Cut,0,sizeof Cut),ans=sccnt=idx=0;
for(int i=1;i<=n;i++) k[i].clear();
}
}
P5058 嗅探器
从一台中心机开始进行 \(\text{Tarjan}\) 求割点
这样我们就只需要考虑另外一个点
显然只有割点可能成为答案
我们判到一个割点时如果此时正好在向下 \(\text{Tarjan}\) 中找到了另外一台
那就会满足 \(dfn[v]>=dfn[Center]\)
这一条可以保证他一定在其子树中而不是以前搜一半结果被这个判掉
注意搞答案时要判掉中心机
#include<bits/stdc++.h>
using namespace std;
const int N=200009;
int n,idx,low[N],dfn[N],A,B;
vector<int> k[N],ans;
void dfs(int i=A){
low[i]=dfn[i]=++idx;
for(int j:k[i]){
if(!dfn[j]){
dfs(j),low[i]=min(low[i],low[j]);
if(low[j]>=dfn[i]&&dfn[j]<=dfn[B]&&i!=A&&i!=B)
ans.push_back(i);
}else low[i]=min(low[i],dfn[j]);
}
}
int main(){
int l,r;
scanf("%d",&n);
while(true){
scanf("%d%d",&l,&r),k[l].push_back(r),k[r].push_back(l);
if(!l)break;
}
scanf("%d%d",&A,&B),dfs();
if(ans.empty()) puts("No solution"),exit(0);
sort(ans.begin(),ans.end()),printf("%d\n",ans[0]);
return 0;
}
LibreOJ 10102. 旅游航道
求割边板子
不知为何 \(\text{Accoders}\) 和一本通都需要暴力清空
#include<bits/stdc++.h>
using namespace std;
const int N=30009;
int ans,idx,dfn[N],low[N];
struct node{int t,d;};
vector<node> k[N];
void dfs(int i,int f){
dfn[i]=low[i]=++idx;
for(node j:k[i]){
if(!dfn[j.t]){
dfs(j.t,j.d),low[i]=min(low[i],low[j.t]);
if(low[j.t]>dfn[i])++ans;
}else if(j.d!=f) low[i]=min(low[i],dfn[j.t]);
}
}
int main(){
int n,m,l,r;
while(true){
scanf("%d%d",&n,&m); if(!n) return 0;
for(int i=1;i<=m;i++) scanf("%d%d",&l,&r),k[l].push_back({r,i}),k[r].push_back({l,i});
for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i,-1);
printf("%d\n",ans);
memset(dfn,0,sizeof dfn),memset(low,0,sizeof low),ans=idx=0;
for(int i=1;i<=N-2;i++) k[i].clear();
}
return 0;
}
LibreOJ 10103. 电力
求割点板子
找出一个割点最多在几个点双里即可
有可能需要记录原来有几个连通块
还需要特判没有边全都是孤立点的情况
#include<bits/stdc++.h>
#define debug printf("cut %d\n",i)
using namespace std;
const int N=10009;
int ans,idx,dfn[N],low[N],maxi;
vector<int> k[N];
void dfs(int i,int f){
int tmp=0,son=0;
dfn[i]=low[i]=++idx;
for(int j:k[i]){
if(!dfn[j]){
++son;
dfs(j,1),low[i]=min(low[i],low[j]);
if(low[j]>=dfn[i]&&f!=0)++tmp;
}else low[i]=min(low[i],dfn[j]);
}
maxi=max(maxi,tmp);
if(f==0)maxi=max(maxi,son-1);
}
int main(){
int n,m,l,r;
while(true){
scanf("%d%d",&n,&m); if(!n) return 0; if(!m){printf("%d\n",n-1);continue;}
for(int i=1;i<=m;i++)
scanf("%d%d",&l,&r),++l,++r,k[l].push_back(r),k[r].push_back(l);
for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i,0),++ans;
printf("%d\n",ans+maxi);
memset(dfn,0,sizeof dfn),memset(low,0,sizeof low);
ans=idx=maxi=0;
for(int i=1;i<=N-2;i++) k[i].clear();
}
return 0;
}
P3469 Blockade
良心题目
联通简单图
讨论每个点是否是割点
不是割点 \(ans=2n-2\)
是割点 \(ans=2(size_1*size_2+(size_1+size_2)*size_3+...)\)
其中 \(size\) 不含割点
#include<bits/stdc++.h>
using namespace std;
const int N=100009;
typedef long long ll;
vector<int> k[N];
ll ans[N];
int idx,low[N],dfn[N],size[N],n;
void dfs(int i){
ll cnt=0;
int son=0;
size[i]=1,low[i]=dfn[i]=++idx,ans[i]=n-1;
for(int j:k[i]){
if(!dfn[j]){
++son;
dfs(j),low[i]=min(low[i],low[j]),size[i]+=size[j];
if(low[j]>=dfn[i]) ans[i]+=cnt*size[j],cnt+=size[j];
}else low[i]=min(low[i],dfn[j]);
}
if(cnt) ans[i]+=(n-cnt-1)*cnt;
ans[i]*=2;
}
int main(){
int m,l,r;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
scanf("%d%d",&l,&r),k[l].push_back(r),k[r].push_back(l);
dfs(1);
for(int i=1;i<=n;i++) printf("%lld\n",ans[i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号