Manacher

A Simple Problem

这个问题的原型很简单
给你一个字符串
让你求他的最长回文子串
这把我们先放模板题

你可能会说：这题我会啊！
两边 \(\text{Hash}\) 加二分
\(O(n \log n)\) 这么优秀的复杂度还过不了吗？

然而并不行
\(10^7\) 的数据
除非你用的是 \(\text{LOJ}\) 神机
否则你可能需要一个线性算法

如果你是一个巨佬
你可能会说：线性我也会啊
然后你就码起了一些奇奇怪怪的算法
虽然但是巨佬应该会 manacher。。。
但其实，有一个更好写并且更快的算法

接下来，我们正式进入我们的 \(\text{manacher}\) 阶段

Manacher

我们发现
奇数长度的回文串要算一次
偶数长度也要算一次
非常麻烦
于是 \(\text{OI}\) 大佬搞了一个很好的方法
就是插入隔断字符

比如原来有两个串分别是
\(\text{ABA}\) 和 \(\text{ABBA}\)
隔断之后就变成了
\(\text{@A@B@A@}\) 和 \(\text{@A@B@B@A@}\)
然后统计答案的时候再判一判搞一搞就可以了
不用整两次数组
非常的 \(\text{nice}\)

下一步咋整呢？
接下来最容易想到的就是从每个中心开始
然后向两边枚举
加下来思考如何优化
二分加哈希还是先算了
优化基本都是一点
就是利用原来求过的信息进行乱搞

所以有一个很自然的思路
就是存一下每个点向外扩展能达到的最大长度
我们叫他 \(Man_i\)
比如说一个串 \(\text{@A@B@C@B@A@B@A@}\)
(下标从一开算)
举两个例子
\(Man_6=5,Man_2=1,Man_{12}=3\)

这里都很简单
下一步比较离谱
我们需要维护一个 以前算过的 右端点最靠右的 它是由哪一个点向外扩展得到的
比如说我们枚举到了上一个串的第七个位置
那么我们最右端点就是那个 \(C\) 扩展出的 \(S_{11}\)
我们记录最右端点 \(Lim=11\) 和他的中心 \(Mid=6\)
然后我们分成两种情况

1. \(i>Lim\) 这种情况直接暴力扩展，非常的简单
2. \(i<=Lim\)
   我们有一个非常好的想法
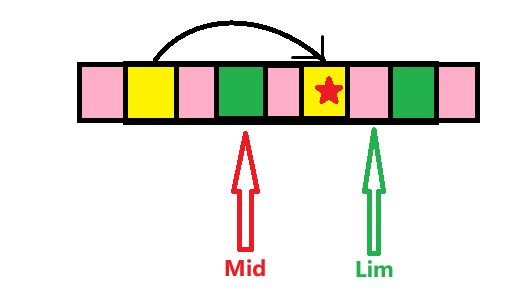
   如图
   

那个带五角星的就是当前的位置
我们发现他其实可以用它 “对称点” 的信息直接转移
就像图中这样
我们直接从他 "对称点" 的长度往下转移即可
而没有必要一个一个暴力的整
能快一些

这看起来非常好
只是有一个小小的问题
你都不用使劲想去构造数据都知道他并不对
比如说一个简单的数据
\(@I@R@\ T@R@I\ @E@I@\ R@T@M\ @N\)
(空格只是方便数下标)
这个字符串
当你枚举 \(i=19\) 的时候
显然此时 \(Mid=12,Lim=19\)
但如果你直接从其 "对称点" \(Man_6=5\) 开始枚举的话
你就会发现她甚至直接就 \(\text{RE}\) 了

为啥呢
因为在 \(Mid\) 的管辖范围之外，两边的东西其实是随意加的
我们之所以刚才的可以扩展是因为他左右两边是有一个对称关系的
但外面套路深所以管辖范围之外并没有这样的对称关系，所以不能瞎整
所以我们转移的时候其实还要和 \(Mid\) 的管辖范围取最小值

然后就没有了
这看起来非常像一个常数优化
甚至让人感觉它并没有哈希二分快
但是时间复杂度确实是线性。。。
笑死根本不会搞

其实它的难度很低
基本和 \(KMP\) 差不多。。。
所以不要害怕
干就完了

还有一个小点
就是我们一般都在开头和结尾插入一个特殊字符
防止 \(\text{RE}\)

最后一点：
我们输出的答案是什么？
如果中间是一个间隔符 \(@\) 的话
显然间隔符会比实际字符多一个
如果中间不是间隔符的话
那么也是一样的
所以我们串的总长度是 \(Man[i]*2+1\)
减一除以二之后直接输出 \(\max{Man_i}\) 即可

Code

P3805 模板

#include<bits/stdc++.h>
using namespace std;
const int N=22000009;
char s[N];
int n,Man[N],Mid=0,Lim=0,ans=-1;
void Scan(){
	char k=getchar();
	s[++n]='~';
	while(k>='a'&&k<='z')s[++n]='@',s[++n]=k,k=getchar();
	s[++n]='@',s[++n]='^';
//	printf("solved:%s\n",s+1);
}
int main(){
	Scan();
	for(int i=2,it;i<n;i++){
		if(i>Lim){
			Mid=i,it=0;
			while(s[i+it+1]==s[i-it-1])++it;
			Lim=i+it,Man[i]=it;
		}else{
			it=min(Lim-i,Man[(Mid<<1)-i]);
			while(s[i+it+1]==s[i-it-1])++it;
			Man[i]=it;
			if(i+it>Lim)Mid=i,Lim=i+it;
		}
		//printf("Man[%d]=%d\n",i,Man[i]);
		ans=max(ans,Man[i]);
	}
	printf("%d",ans);
	return 0;
}