树链剖分基础
著名毒瘤算法,以码量惊人而著称
思路还可以
觉得比 \(Tarjan\) 简单一些
前置知识:线段树基础
\(Now\ Let's\ Start\)
Part 1 A Tree
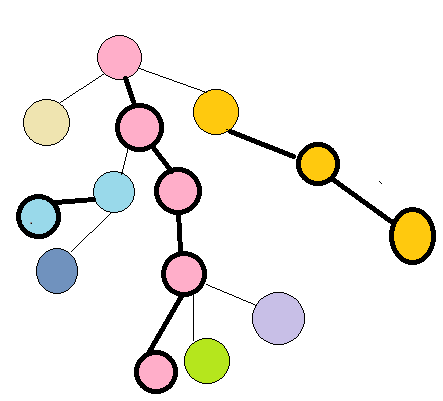
如图是一颗五颜六色的树
还给了我们这样一个问题
P3384 【模板】重链剖分/树链剖分
要求实现以下四种操作:
一、将树从 x 到 y 结点最短路径上所有节点的值都加上 z
二、求树从 x 到 y 结点最短路径上所有节点的值之和。
三、将以 x 为根节点的子树内所有节点值都加上 z。
四、求以 x 为根节点的子树内所有节点值之和。
笑死,暴力都不会
单纯求子树的话可以树形 \(DP\)
求路径也可以 \(LCA\) 乱搞
但这两个都不支持修改
我们看一下后面
修改。。。求和。。。
线段树!
线段树可以,可是线段树是不好树上直接搞的
显然我们需要把他展平,成为一个数组
这时你不禁要问:直接按节点编号整一下不就行了
然而并不行
这样展好之后路径和子树都是分散的只能单修
但你每个都单修我直接暴力不香吗还少一个 \(log\)
现在我们看到了问题所在
说白了我们想找一种方法把展开的序列尽可能 “连续”
重链剖分就是一种解决方案
具体过程(\(OI\)-\(Wiki\)):
重儿子是一个节点子节点中子树最大的结点,其余即为轻儿子。
如果有多个子树最大的子结点,取其一。
从这个结点到重子节点的边为重边。
到其他轻子节点的边为轻边。
若干条首尾衔接的重边构成重链。
把落单的结点也当作重链,那么整棵树就被剖分成若干条重链。
这个描述有些抽象
So 我们看一下那棵树
显然你已经注意到它的颜色和特殊标记的链条了
这棵树同一颜色就是同一条重链
重链和重儿子也已经被加粗了
你会发现一些性质
- 一个单独的节点可能是一条重链
- 重链一定由轻儿子开始
- 任意一个节点到根节点至多经过 \(\log_2{n}\) 条重链
性质三证明
由于每次切换重链时代表这条边不是重边(显然)
那么该节点就是一个轻儿子
说明还有一个子树大小至少与当前节点相等的重儿子
即子树大小至少翻倍
由此得证
然后你会发现任意一条树上路径都只会经过 log 条(常数忽略)
这看起来很好
你只需要保证重链的标号连续即可
SO 我们想到使用 DFS 序来求解
每次优先走重儿子来保证 DFN 连续
然后一和二就可以转化成线段树问题(细节一会再说)
三和四呢?
你会发现 DFN 还有一个好处
由于 DFS 的性质
所以子树的 DFN 也是连续的
然后就没有然后了
Part 2 Many Chains
当我们刨分完成之后
显然子树很简单直接 +size-1 即可
但路径还是有难度的

假设我们现在想要去求 \(AB\) 两点之间的路径和
首先我们遇到了一个问题:先走哪个?
根据玄学 我们每次都跳当前链的顶端深度较大的到上一条重链
这样是对的
是的
然而我并不知道为何
其过程如图所示
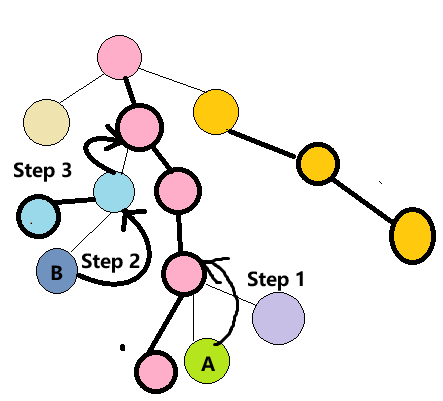
最终我们会发现这两个点跳到了同一条重链上
我们在跳的过程中统计答案
最后加上一小段即可
你会发现这个东西还可以求 LCA
然后就没了
接下来我们把刚才的题码了
#include<bits/stdc++.h>
using namespace std;
const int N=200009;
//Scan Part
typedef long long ll;
ll Mod; int h[N],cnt,val[N],n,T,rt;
struct Node{int i,o;}k[N];
inline void add(int u,int v){k[++cnt]={v,h[u]},h[u]=cnt;}
void Scan(){
int u,v;
scanf("%d%d%d%lld\n",&n,&T,&rt,&Mod);
for(int i=1;i<=n;i++)scanf("%d",&val[i]),h[i]=-1;
for(int i=1;i<n;i++)scanf("%d%d",&u,&v),add(u,v),add(v,u);
}
//Basic DFS Part
int son[N],dep[N],fa[N],siz[N];
void Basic(int i=rt,int f=0){
fa[i]=f,dep[i]=dep[f]+1,siz[i]=1;
for(int it=h[i],v;~it;it=k[it].o){
v=k[it].i;
if(v==f)continue;
Basic(v,i),siz[i]+=siz[v];
if(siz[v]>siz[son[i]])son[i]=v;
}
}
//Cut DFS Part
int dfn[N],kth[N],top[N],shit;
void Cut(int i=rt,int tmp=rt){
dfn[i]=++shit,kth[shit]=i,top[i]=tmp;
if(son[i])Cut(son[i],tmp);
for(int it=h[i],v;~it;it=k[it].o){
v=k[it].i;
if(v==fa[i]||v==son[i])continue;
Cut(v,v);
}
}
//Segment Tree Part
class Segment{
public:
void Build(int i,int l,int r){
if(l==r){a[i]=val[kth[l]]%Mod;return;}
int ls=i<<1,rs=i<<1|1,mid=(l+r)>>1;
Build(ls,l,mid),Build(rs,mid+1,r);
a[i]=(a[ls]+a[rs])%Mod;
}
void Add(int i,int l,int r,int L,int R,ll K){
if(l==L&&r==R){a[i]=(a[i]+K%Mod*(r-l+1)%Mod)%Mod,tag[i]=(tag[i]+K)%Mod;return;}
Pd(i,l,r);
int ls=i<<1,rs=i<<1|1,mid=(l+r)>>1;
if(R<=mid)Add(ls,l,mid,L,R,K);
else if(L>mid)Add(rs,mid+1,r,L,R,K);
else Add(ls,l,mid,L,mid,K),Add(rs,mid+1,r,mid+1,R,K);
a[i]=(a[ls]+a[rs])%Mod;
}
ll Query(int i,int l,int r,int L,int R){
if(l==L&&r==R)return a[i];
Pd(i,l,r);
int ls=i<<1,rs=i<<1|1,mid=(l+r)>>1;
if(R<=mid)return Query(ls,l,mid,L,R);
else if(L>mid) return Query(rs,mid+1,r,L,R);
else return (Query(ls,l,mid,L,mid)+Query(rs,mid+1,r,mid+1,R))%Mod;
}
private:
ll a[N<<2],tag[N<<2];
inline void Pd(int i,int l,int r){
if(!tag[i])return;
int ls=i<<1,rs=i<<1|1,mid=(l+r)>>1;
tag[ls]=(tag[ls]+tag[i])%Mod;
tag[rs]=(tag[rs]+tag[i])%Mod;
a[ls]=(a[ls]+tag[i]*(mid-l+1))%Mod;
a[rs]=(a[rs]+tag[i]*(r-mid))%Mod;
tag[i]=0;
}
}t;
void Solve(){
int op,x,y,z;
t.Build(1,1,n);
while(T--){
scanf("%d",&op);
if(op==1){
scanf("%d%d%d",&x,&y,&z);
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
t.Add(1,1,n,dfn[top[x]],dfn[x],z);
x=fa[top[x]];
}
if(dfn[x]>dfn[y])swap(x,y);
t.Add(1,1,n,dfn[x],dfn[y],z);
}else if(op==2){
scanf("%d%d",&x,&y);
ll ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
ans=(ans+t.Query(1,1,n,dfn[top[x]],dfn[x]))%Mod;
x=fa[top[x]];
}
if(dfn[x]>dfn[y])swap(x,y);
printf("%lld\n",(ans+t.Query(1,1,n,dfn[x],dfn[y]))%Mod);
}else if(op==3){
scanf("%d%d",&x,&z);
t.Add(1,1,n,dfn[x],dfn[x]+siz[x]-1,z);
}else if(op==4){
scanf("%d",&x);
printf("%lld\n",t.Query(1,1,n,dfn[x],dfn[x]+siz[x]-1));
}
// for(int i=1;i<=n;i++)printf("%lld ",t.Query(1,1,n,dfn[i],dfn[i]));
// puts("<");
}
}
int main(){
Scan();
Basic();
Cut();
Solve();
return 0;
}
例题
Example 01 [P2590 树的统计]
唐氏模板题目
我们借这题来说一下我们的树剖结构
读入部分
//Scan Part
struct node{int i,o;}a[N];
int n,h[N],val[N],cnt;
inline void add(int u,int v){a[++cnt]={v,h[u]},h[u]=cnt;}
void Scan(){
int u,v;
scanf("%d",&n);
for(int i=1;i<=n;i++)h[i]=-1;
for(int i=1;i<n;i++)scanf("%d%d",&u,&v),add(u,v),add(v,u);
for(int i=1;i<=n;i++)scanf("%d",&val[i]);
}
首先是第一次基础DFS
确定父子关系 (fa 数组)、子树大小 (siz 数组)、节点深度和重儿子
//Scan Part
struct node{int i,o;}a[N];
int n,h[N],val[N],cnt;
inline void add(int u,int v){a[++cnt]={v,h[u]},h[u]=cnt;}
void Scan(){
int u,v;
scanf("%d",&n);
for(int i=1;i<=n;i++)h[i]=-1;
for(int i=1;i<n;i++)scanf("%d%d",&u,&v),add(u,v),add(v,u);
for(int i=1;i<=n;i++)scanf("%d",&val[i]);
}
接着是树剖 DFS
搞出重链开端和 DFS 序,DFS 序对应值
//Cut Dfs
int top[N],dfn[N],kth[N],idx;
void Cut(int i=1,int rt=1){
top[i]=rt,dfn[i]=++idx,kth[idx]=i;
if(son[i])Cut(son[i],rt);
for(int it=h[i];~it;it=a[it].o){
if(a[it].i==fa[i]||a[it].i==son[i])continue;
Cut(a[it].i,a[it].i);
}
}
接着是线段树
//Segment Tree Part
class Segment{
public:
void Build(int i,int l,int r){
if(l==r){big[i]=k[i]=val[kth[l]];return;}
int ls=i<<1,rs=i<<1|1,mid=(l+r)>>1;
Build(ls,l,mid),Build(rs,mid+1,r);
k[i]=k[ls]+k[rs],big[i]=max(big[ls],big[rs]);
}
void Modify(int i,int l,int r,int d,int x){
if(l==r){k[i]=big[i]=x;return;}
int ls=i<<1,rs=i<<1|1,mid=(l+r)>>1;
if(d<=mid)Modify(ls,l,mid,d,x); else Modify(rs,mid+1,r,d,x);
k[i]=k[ls]+k[rs],big[i]=max(big[ls],big[rs]);
}
int Qmax(int i,int l,int r,int L,int R){
if(!i)puts("Holy Shit"),exit(0);
if(l==L&&r==R)return big[i];
int ls=i<<1,rs=i<<1|1,mid=(l+r)>>1;
if(R<=mid)return Qmax(ls,l,mid,L,R);
else if(L>mid)return Qmax(rs,mid+1,r,L,R);
else return max(Qmax(ls,l,mid,L,mid),Qmax(rs,mid+1,r,mid+1,R));
}
long long Qsum(int i,int l,int r,int L,int R){
if(!i)puts("Holy Shit"),exit(0);
if(l==L&&r==R)return k[i];
int ls=i<<1,rs=i<<1|1,mid=(l+r)>>1;
if(R<=mid)return Qsum(ls,l,mid,L,R);
else if(L>mid)return Qsum(rs,mid+1,r,L,R);
else return Qsum(ls,l,mid,L,mid)+Qsum(rs,mid+1,r,mid+1,R);
}
private:
int k[N<<2],big[N<<2];
}t;
AC Code
#include<bits/stdc++.h>
using namespace std;
const int N=100009;
//Scan Part
struct node{int i,o;}a[N];
int n,h[N],val[N],cnt;
inline void add(int u,int v){a[++cnt]={v,h[u]},h[u]=cnt;}
void Scan(){
int u,v;
scanf("%d",&n);
for(int i=1;i<=n;i++)h[i]=-1;
for(int i=1;i<n;i++)scanf("%d%d",&u,&v),add(u,v),add(v,u);
for(int i=1;i<=n;i++)scanf("%d",&val[i]);
}
//Basic DFS
int son[N],siz[N],fa[N],dep[N];
void Basic(int i=1,int f=0){
fa[i]=f,siz[i]=1,dep[i]=dep[f]+1;
for(int it=h[i],v;~it;it=a[it].o){
if(a[it].i==f)continue;
v=a[it].i;
Basic(v,i);
siz[i]+=siz[v];
if(siz[v]>siz[son[i]])son[i]=v;
}
}
//Cut Dfs
int top[N],dfn[N],kth[N],idx;
void Cut(int i=1,int rt=1){
top[i]=rt,dfn[i]=++idx,kth[idx]=i;
if(son[i])Cut(son[i],rt);
for(int it=h[i];~it;it=a[it].o){
if(a[it].i==fa[i]||a[it].i==son[i])continue;
Cut(a[it].i,a[it].i);
}
}
//Segment Tree Part
class Segment{
public:
void Build(int i,int l,int r){
if(l==r){big[i]=k[i]=val[kth[l]];return;}
int ls=i<<1,rs=i<<1|1,mid=(l+r)>>1;
Build(ls,l,mid),Build(rs,mid+1,r);
k[i]=k[ls]+k[rs],big[i]=max(big[ls],big[rs]);
}
void Modify(int i,int l,int r,int d,int x){
if(l==r){k[i]=big[i]=x;return;}
int ls=i<<1,rs=i<<1|1,mid=(l+r)>>1;
if(d<=mid)Modify(ls,l,mid,d,x); else Modify(rs,mid+1,r,d,x);
k[i]=k[ls]+k[rs],big[i]=max(big[ls],big[rs]);
}
int Qmax(int i,int l,int r,int L,int R){
if(!i)puts("Holy Shit"),exit(0);
if(l==L&&r==R)return big[i];
int ls=i<<1,rs=i<<1|1,mid=(l+r)>>1;
if(R<=mid)return Qmax(ls,l,mid,L,R);
else if(L>mid)return Qmax(rs,mid+1,r,L,R);
else return max(Qmax(ls,l,mid,L,mid),Qmax(rs,mid+1,r,mid+1,R));
}
long long Qsum(int i,int l,int r,int L,int R){
if(!i)puts("Holy Shit"),exit(0);
if(l==L&&r==R)return k[i];
int ls=i<<1,rs=i<<1|1,mid=(l+r)>>1;
if(R<=mid)return Qsum(ls,l,mid,L,R);
else if(L>mid)return Qsum(rs,mid+1,r,L,R);
else return Qsum(ls,l,mid,L,mid)+Qsum(rs,mid+1,r,mid+1,R);
}
private:
int k[N<<2],big[N<<2];
}t;
//Solve Part
void Solve(){
int T,a,b;
char op[100];
scanf("%d",&T),t.Build(1,1,n);
while(T--){
scanf("%s%d%d",op,&a,&b);
if(op[1]=='H'){
t.Modify(1,1,n,dfn[a],b);
}else if(op[1]=='M'){
int ans=INT_MIN;
while(top[a]!=top[b]){
if(dep[top[a]]<dep[top[b]])swap(a,b);
ans=max(ans,t.Qmax(1,1,n,dfn[top[a]],dfn[a]));
a=fa[top[a]];
}
if(dfn[a]>dfn[b])swap(a,b);
printf("%d\n",max(ans,t.Qmax(1,1,n,dfn[a],dfn[b])));
}
else if(op[1]=='S'){
long long ans=0;
while(top[a]!=top[b]){
if(dep[top[a]]<dep[top[b]])swap(a,b);
ans+=t.Qsum(1,1,n,dfn[top[a]],dfn[a]);
a=fa[top[a]];
}
if(dfn[a]>dfn[b])swap(a,b);
printf("%lld\n",ans+t.Qsum(1,1,n,dfn[a],dfn[b]));
}
}
}
int main(){
Scan();
Basic();
Cut();
Solve();
return 0;
}
Example 03 [ACP2172 软件包管理器]
唐氏模板
#include<bits/stdc++.h>
#define install int ls=i<<1,rs=i<<1|1,mid=(l+r)>>1
using namespace std;
const int N=100089;
int fa[N],siz[N],n,son[N],dep[N],top[N],dfn[N],kth[N],idx;
vector<int> a[N];
void Scan(){
scanf("%d",&n);
for(int i=2;i<=n;i++)scanf("%d",&fa[i]),++fa[i],a[fa[i]].push_back(i);
}
void Basic(int i=1){
siz[i]=1,dep[i]=dep[fa[i]]+1;
for(int it:a[i]){
Basic(it),siz[i]+=siz[it];
if(siz[it]>siz[son[i]])son[i]=it;
}
}
void Cut(int i=1,int rt=1){
dfn[i]=++idx,kth[idx]=i,top[i]=rt;
//printf("dfn %d is %d\n",i,idx);
if(son[i])Cut(son[i],rt);
for(int it:a[i]){
if(it==son[i])continue;
Cut(it,it);
}
}
class Segment{
public:
void Modify(int i,int l,int r,int L,int R,int K){
if(l==L&&r==R){tag[i][K]=1,tag[i][1-K]=0,k[i]=(r-l+1)*K;return;}
Pd(i,l,r);
install;
if(R<=mid)Modify(ls,l,mid,L,R,K);
else if(L>mid)Modify(rs,mid+1,r,L,R,K);
else Modify(ls,l,mid,L,mid,K),Modify(rs,mid+1,r,mid+1,R,K);
k[i]=k[ls]+k[rs];
}
int Query(int i,int l,int r,int L,int R){
if(l==L&&r==R)return k[i];
Pd(i,l,r);
install;
if(R<=mid)return Query(ls,l,mid,L,R);
else if(L>mid)return Query(rs,mid+1,r,L,R);
else return Query(ls,l,mid,L,mid)+Query(rs,mid+1,r,mid+1,R);
}
private:
int k[N<<2],tag[N<<2][3];
void Pd(int i,int l,int r){
if((tag[i][1]|tag[i][0])==false)return;
install;
tag[ls][0]=tag[rs][0]=tag[i][0];
tag[ls][1]=tag[rs][1]=tag[i][1];
int tmp=(tag[i][0])?0:1;
k[ls]=(mid-l+1)*tmp,k[rs]=(r-mid)*tmp;
tag[i][0]=tag[i][1]=0;
}
}t;
void Solve(){
// for(int i=1;i<=n;i++){
// printf("id %d\n",i);
// printf("fa %d\nson",fa[i]);
// for(int j:a[i])printf("%d ",j);
// puts("\n");
// }
int T,x;
char op[102];
scanf("%d",&T);
// for(int i=1;i<=n;i++)printf("%d ",t.Query(1,1,n,dfn[i],dfn[i]));
// puts("<");
while(T--){
scanf("%s%d",op,&x),++x;
if(op[0]=='u'){
printf("%d\n",t.Query(1,1,n,dfn[x],dfn[x]+siz[x]-1));
t.Modify(1,1,n,dfn[x],dfn[x]+siz[x]-1,0);
}else{
int tot=0,num=0;
//puts("Installing......");
while(x){
//printf("goto %d!\n",x);
tot+=dep[x]-dep[top[x]]+1;
num+=t.Query(1,1,n,dfn[top[x]],dfn[x]);
t.Modify(1,1,n,dfn[top[x]],dfn[x],1);
//printf("installing %d[%d] ~ %d[%d]...\n",top[x],dfn[top[x]],x,dfn[x]);
x=fa[top[x]];
}
printf("%d\n",tot-num);
}
// for(int i=1;i<=n;i++)printf("%d ",t.Query(1,1,n,dfn[i],dfn[i]));
// puts("<");
}
}
int main(){
Scan();
Basic();
Cut();
Solve();
return 0;
}
//1
//2->1
//3->1
//4->1
//5->2
//6->2
//7->6
Example 04 [ACP2173 染色]
树剖线段树显然
难点在于如何合并信息
但你要注意他是树剖练习而非点分治,所以他求的是颜色段而非不同颜色
那就不难啦
我们特判一下每一段的左右边界就好
然后你可以倒回去看一下我们求路径的部分
我们动态维护当前的左右颜色就可以了
这题看思路一点不难
下面祭出蒟蒻 \(3\) 小时的战果
无压行
#include<bits/stdc++.h>
#define install int ls=i<<1,rs=i<<1|1,mid=(l+r)>>1
using namespace std;
const int N=400009;
namespace Basic{
int n,c[N],s[N],h[N],d[N],t[N],p[N],rk[N],fa[N],idx;
//color size heavy dfn top dep
vector<int> o[N];
void dfs(int i,int f){
s[i]=1,p[i]=p[f]+1,fa[i]=f;
for(int j:o[i]) if(j!=f){
dfs(j,i),s[i]+=s[j];
if(s[j]>s[h[i]])h[i]=j;
}
}
void cut(int i,int rt,int f){
d[i]=++idx,rk[idx]=i,t[i]=rt;
// printf("top of %d is %d\n",i,rt);
if(h[i])cut(h[i],rt,i);
for(int j:o[i]) if(j!=f&&j!=h[i]) cut(j,j,i);
}
}
using Basic::c;
using Basic::rk;
class Segment{
public:
void b(int i,int l,int r){
if(l==r){ll[i]=rr[i]=c[rk[l]],k[i]=1;return;}
install;
b(ls,l,mid),b(rs,mid+1,r),pu(i,ls,rs);
}
void m(int i,int l,int r,int L,int R,int D){
if(L==l&&r==R){ll[i]=rr[i]=t[i]=D,k[i]=1;/*printf("%d to %d [%d,%d]\n",rk[l],rk[r],ll[i],rr[i]);*/return;}
install;
pd(i,ls,rs);
if(R<=mid)m(ls,l,mid,L,R,D);
else if(L>mid)m(rs,mid+1,r,L,R,D);
else m(ls,l,mid,L,mid,D),m(rs,mid+1,r,mid+1,R,D);
pu(i,ls,rs);
}
int q(int i,int l,int r,int L,int R,int &_l,int &_r){
if(l==L&&r==R){_l=ll[i],_r=rr[i];return k[i];}
install;
pd(i,ls,rs);
if(R<=mid)return q(ls,l,mid,L,R,_l,_r);
else if(L>mid)return q(rs,mid+1,r,L,R,_l,_r);
else{
int tl,tr;
return q(ls,l,mid,L,mid,_l,tl)+q(rs,mid+1,r,mid+1,R,tr,_r)-(int)(tl==tr);
}
}
private:
int k[N<<2],t[N<<2],ll[N<<2],rr[N<<2];
void pu(int i,int ls,int rs){ll[i]=ll[ls],rr[i]=rr[rs],k[i]=k[ls]+k[rs]-(int)(rr[ls]==ll[rs]);}
void pd(int i,int ls,int rs){
if(t[i]==0)return;
ll[ls]=rr[ls]=ll[rs]=rr[rs]=t[ls]=t[rs]=t[i],k[ls]=k[rs]=1,t[i]=0;
}
}T;
using namespace Basic;
int main(){
int m,l,r,w;
char op[4];
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&c[i]);
for(int i=1;i<n;i++)scanf("%d%d",&l,&r),o[l].push_back(r),o[r].push_back(l);
dfs(1,0),cut(1,1,0),T.b(1,1,n);
// for(int i=1,a,b;i<=n;i++){
// T.q(1,1,n,d[i],d[i],a,b);
// printf("%d(%d) ",a,b);
// }
// puts("");
while(m--){
scanf("%s",op);
if(op[0]=='C'){
scanf("%d%d%d",&l,&r,&w);
while(t[l]!=t[r]){
if(p[t[l]]<p[t[r]])swap(l,r);
// printf("mark %d - %d\n",t[l],l);
T.m(1,1,n,d[t[l]],d[l],w),l=fa[t[l]];
}
if(p[l]>p[r])swap(l,r);
T.m(1,1,n,d[l],d[r],w);
// for(int i=1,a,b;i<=n;i++){
// T.q(1,1,n,d[i],d[i],a,b);
// printf("%d(%d) ",a,b);
// }
// puts("");
}else{
scanf("%d%d",&l,&r);
int lr=-1,rl=-2,ans=0,tl,tr;
while(t[l]!=t[r]){
if(p[t[l]]>p[t[r]]) ans+=T.q(1,1,n,d[t[l]],d[l],tr,tl),l=fa[t[l]],ans-=(int)(tl==lr),lr=tr;
else ans+=T.q(1,1,n,d[t[r]],d[r],tl,tr),r=fa[t[r]],ans-=(int)(tr==rl),rl=tl;
}
if(d[l]<d[r])ans+=T.q(1,1,n,d[l],d[r],tl,tr); else ans+=T.q(1,1,n,d[r],d[l],tr,tl);
ans-=(int)(lr==tl)+(int)(rl==tr);
printf("%d\n",ans);
}
}
return 0;
}
Example 05 [ACP2174 旅行]
给定一棵树
每个点都有一个颜色 \(c\) 和权值 \(v\)
有四种操作
两种分别是改变其颜色或权值
还有两种是在两点的最短路径上找出给定颜色的点的权值和或权值最大值、
颜色不超过 \(10^5\) 种
询问和点数范围同上
Solution
思考对每一个颜色搞一颗线段树
然后在链上维护对应颜色的 \(\text{sum}\) 和 \(\text{max}\)
前两个操作单点修改,后两个区间查询
这样可以但是空间不够
所以我们动态开点
每次把对应的节点搞到对应颜色的线段树里即可
这样空间是 \(O(n\log n)\) 的
#include<bits/stdc++.h>
using namespace std;
const int N=100009;
vector<int> k[N];
int c[N],v[N],dep[N],fa[N],top[N],siz[N],son[N],dfn[N],kth[N],cnt,ls[N*17],rs[N*17],lim[N*17],idx,sum[N*17];
void DFS(int i=1,int f=0){
fa[i]=f,dep[i]=dep[f]+1,siz[i]=1;
for(int j:k[i]) if(j!=f){
DFS(j,i),siz[i]+=siz[j];
if(siz[j]>siz[son[i]])son[i]=j;
}
}
void CUT(int i=1,int rt=1){
top[i]=rt,dfn[i]=++cnt,kth[cnt]=i;
if(son[i])CUT(son[i],rt);
for(int j:k[i]) if(j!=son[i]&&j!=fa[i]) CUT(j,j);
}
struct T{
int rt=0;
void modify(int &i,int l,int r,int d,int x){
if(!i)i=++idx; if(l==r){lim[i]=sum[i]=x;return;}
int mid=(l+r)>>1;
if(d<=mid) modify(ls[i],l,mid,d,x); else modify(rs[i],mid+1,r,d,x);
sum[i]=sum[ls[i]]+sum[rs[i]],lim[i]=max(lim[ls[i]],lim[rs[i]]);
}
int querys(int i,int l,int r,int L,int R){
if(!i)return 0; if(L==l&&R==r)return sum[i];
int mid=(l+r)>>1;
if(R<=mid) return querys(ls[i],l,mid,L,R); else if(L>mid)return querys(rs[i],mid+1,r,L,R); else return querys(ls[i],l,mid,L,mid)+querys(rs[i],mid+1,r,mid+1,R);
}
int queryl(int i,int l,int r,int L,int R){
if(!i)return INT_MIN; if(L==l&&R==r)return lim[i];
int mid=(l+r)>>1;
if(R<=mid) return queryl(ls[i],l,mid,L,R); else if(L>mid)return queryl(rs[i],mid+1,r,L,R); else return max(queryl(ls[i],l,mid,L,mid),queryl(rs[i],mid+1,r,mid+1,R));
}
}t[N];
int main(){
int n,m,l,r,ans,tmp;char op[4];
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d%d",&v[i],&c[i]);
for(int i=1;i<n;i++)scanf("%d%d",&l,&r),k[l].push_back(r),k[r].push_back(l);
DFS(),CUT();
for(int i=1;i<=n;i++)t[c[i]].modify(t[c[i]].rt,1,n,dfn[i],v[i]);
while(m--){
scanf("%s%d%d",op,&l,&r);
if(op[1]=='C') t[c[l]].modify(t[c[l]].rt,1,n,dfn[l],0),c[l]=r,t[c[l]].modify(t[c[l]].rt,1,n,dfn[l],v[l]);
else if(op[1]=='W') v[l]=r,t[c[l]].modify(t[c[l]].rt,1,n,dfn[l],v[l]);
else if(op[1]=='S'){
ans=0,tmp=c[l];
while(top[l]!=top[r]){
if(dep[top[l]]<dep[top[r]])swap(l,r);
ans+=t[tmp].querys(t[tmp].rt,1,n,dfn[top[l]],dfn[l]),l=fa[top[l]];
}
if(dep[l]>dep[r])swap(l,r);
printf("%d\n",ans+t[tmp].querys(t[tmp].rt,1,n,dfn[l],dfn[r]));
}else{
ans=INT_MIN,tmp=c[l];
while(top[l]!=top[r]){
if(dep[top[l]]<dep[top[r]])swap(l,r);
ans=max(ans,t[tmp].queryl(t[tmp].rt,1,n,dfn[top[l]],dfn[l])),l=fa[top[l]];
}
if(dep[l]>dep[r])swap(l,r);
printf("%d\n",max(ans,t[tmp].queryl(t[tmp].rt,1,n,dfn[l],dfn[r])));
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号