斜率优化 DP
前言:
原来我以为数位 DP 已经够邪恶了
直到我遇见了他
毁灭你,与你有何相干。
这是之前寒假集训的最后一节课
而作者由于太蒻了
所以不能说是融会贯通吧至少也可以说是一窍不通
斜优是一个蒟蒻迈向牛马走向神犇的第一步
学会了就可以水好多好多蓝紫题啦!
所以闲话少叙,\(Let's\ Go\)!
前置知识:
能做出一道 DP 橙题
听说过平面直角坐标系
注:关于具体的时间复杂度证明和严格正确性分析
蒟蒻作者实在无能为力
这个好像貌似应该没啥用吧(bushi)(逃)(doge 保命)
所以基本都只会给出感性理解
Example 01[P3195 玩具装箱]
根据一位 \(dalao\) 的启示,斜率优化 \(DP\) 先不用管斜率,先写暴力 \(DP\),再套优化
题意简述:
给出一个数组 \(A\),要求把该数组分成若干段,设每一段左右端点为\([L,R]\),最小化 \(\sum{(R-L+\sum_{i=L}^R{A[i]}-K)^2}\) 的值
其中 \(K\) 为常数
\(1≤n≤5×10^4\)
Solution
首先考虑可以设 \(DP[i]\) 为使第 \(i\) 个元素成为该段末尾的最小代价
显然 \(DP[n]\) 即为答案
容易想到朴素转移
这个转移是 \(O(n^2)\) 的
肯定是会 \(TLE\) 的
思考怎么优化
蒟蒻貌似现在只学了一个单调队列优化
所以我们试试
但是发现有两个问题:
- 这个貌似没有什么可以淘汰的
当然可以直接维护最小值啦 - 关键是一个事情——单纯的 \(DP[j]\) 当然是可以维护 \(Min\)
后面的部分如果不带平方也可以乱搞过
但这个平方……很难搞,非常难搞
平方是要拆的,但怎么拆,非常重要
如果我们直接暴力开干是非常麻烦的
我们根据古希腊掌管CCF的神的启示
将其按照和\(i\)有关,和\(j\)有关和都没有关分类
当然我们给它起个名字
和 \(\ i\) 有关的叫 \(f_i\)
和 \(\ j\) 有关的叫 \(f_j\)
都没关系的叫 \(shit\)
那么我们拆开得到
现在我们先不用管其中的这三个函数分别是啥
作者一开始就是总去先想这个函数
然后成功炸掉了自己的 CPU
接下来用刚才的方法再分一次
别蒙,第一步就是加法交换律和结合律
我们用大写的 $\ F_i\ F_j\ SHIT\ $表示和 \(i\) 有关,和 \(j\) 有关和都无关
得到
当我们现在发现了一个问题
其中有一项 \(2 f_i f_j\) 是既和 \(i\) 有关也和 \(j\) 有关的
那我们没有办法了
但为了统一,我们还是把他分成两个大写的函数
就 \(G_i\ G_j\) 吧(其中的 2 可以随便乘进去一个函数)
那我们就得到了一个式子
接下来我们暂时设当前的 \(j\) 即为最优转移
则还可以去掉这个 \(min\)
直接就是
此时我们发现这个 \(SHIT\) 也可以直接加到 \(F_i\) 或 \(F_j\) 里
于是最简式子即为
你不禁要问了:这一大套究竟有啥用呢?
其实并没有什么用,只是让你烧一会CPU而已
现在看一下我们最后得到的不等式
这个就是斜率优化的模板不等式
斜率优化就是通过一系列操作
将取最小值的复杂度搞到 \(O(1)\)
现在我们终于可以来看看斜率是啥东西了
斜率,按某度某科的说法,是一条直线的倾斜程度
但用人话讲,他就是一条直线的一个参数
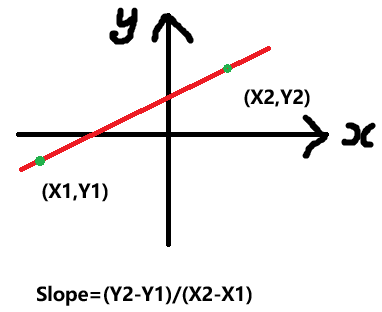
斜率的英文是 \(Slope\),具体求法如图
在一条直线上随意选两个点
用纵坐标之差减去横坐标之差
注意这个斜率是有正负的
所以这个不能瞎减
必须用同一个点作为被减数
但顺序却很无所谓
因为换个顺序分数上下都变成了原来的相反数
分数值并不会变
接下来再介绍一个概念:截距
截距是一条直线与 Y 轴交点的 Y 坐标
具体地讲,如果这条直线的解析式是 \(y=kx+b\)
那么截距就是这个 b
接下来我们在把原来得到的式子转化一下
(此处先不用考虑正负号的问题,因为都可以搞到方程里)
我们发现这个和解析式 \(y=kx+b\) 很像
又由于 \(F_i\) 可以直接 \(O(1)\) 求出
完全可以整体求出最后一项最小值之后再统计答案
然后我们发现这个式子中想要最小化的一项就是我们的截距 b
所以这相当于什么呢
相当于我们每遍历到一个数
都往点集里加了一个点
然后求的最小值相当于每次设定一个统一的斜率
求过这些点直线的最小截距
当然,暴力的想法是遍历每个点求一下
但这样肯定时间复杂度没有变,并不优
思考能否剔除掉一些没有用的点
显然有两种点是完全没有用的
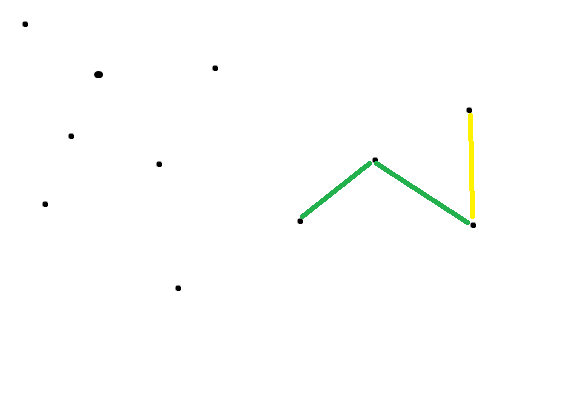
首先是图中黄色线段所连接的两个点
如果他们横坐标相同,那么靠上的点一定不优
其次一种比较难想
见图中两条绿色线段连起来的三个点
严格地说,如果一个平面内有三个点 \(A\ B\ C\)且满足 \(X_A<X_B<X_C\)
设\(S(LINE)\)表示这条线段的斜率
那么如果有 \(S(AB)>S(BC)\)
则 \(B\) 点一定不是最优解
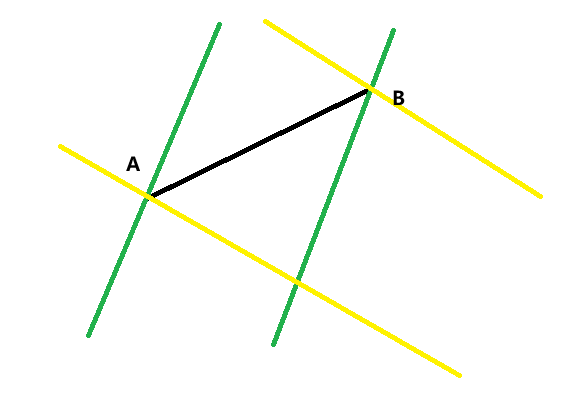
如图的直线 \(AB\)
如果给出的斜率 \(> S(AB)\),靠右的 \(B\) 更优;(绿线)
否则靠左的 \(A\) 更优。(黄线)
有了这个原理我们就可以看看了
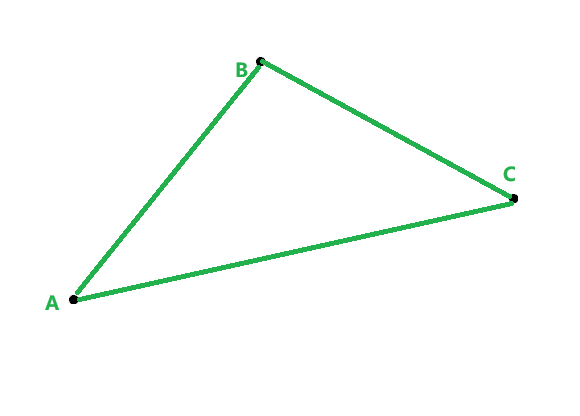
这是我们刚才的那个三角形
可以看出来 \(S(BC)<S(AC)<S(AB)\)
那么我们可知
如果给出的斜率 \(S_0 <= S(AC)\) 则满足 \(S_0<S(AB)\) 此时一定有 A 比 B 优
如果给出的斜率 \(S_0 > S(AC)\) 则满足 \(S_0>S(BC)\) 此时一定有 C 比 B 优
由此得证
这样搞出来的其实就是这个点集的下凸壳
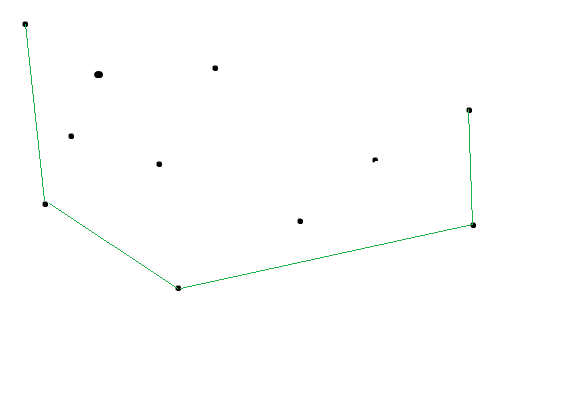
我们可以满足所有可能的转移点点一定在这个下凸壳上
而且也一定满足这些凸壳上的点随着横坐标增大斜率单调递增
这个其实就可以用单调栈/单调队列来维护了
但搞出了凸壳说穿了还是常数优化
但是很多题除了已经列出的性质外还满足两个点
- 给出的点横坐标单调不降
- 给出的斜率同样单调不降
而这才是单调队列的用武之地
再看一眼线段 AB 的图片
我们发现随着给出斜率的增加左面的点越来越容易被淘汰
而如果后面的点已被淘汰那前面的就更白扯了
而当你一通淘汰之后剩下的对头即为最优答案
这就可以用单调队列了
其实有的题不满足如上性质,但也有一些方法进行处理,但作者暂时不会
好了,现在我们重新看一下这道题
这是我们的朴素转移式
我们把它拆开按上面的方法弄一下
这里我们把 \(Sum[x]+x\) 处理出来叫做 \(A[x]\), \(Sum[x]+x-1-K\) 处理出来叫做 \(B[x]\)
原式变为
此时就基本结束了
我们看一下点的信息
\(Point(2A[j],DP[j]+A[j]^2)\)
\(Slope B[i]\)
我们发现 A,B 数组均是单调递增的完美符合性质
So Coding...
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
const int N=50098;
ll dp[N],A[N],B[N];
struct Point{ll x,y;int u;};
//dp[i]=dp[j]+B[i]^2-2B[i]A[j]+A[j]^2
//dp[j]+A[j]^2=B[i]*2A[j]+(dp[i]-B[i]^2)
//Point(2A[j],dp[j]+A[j]^2)
inline Point mp(ll x,ll y,int u){Point tmp;tmp.x=x,tmp.y=y,tmp.u=u;return tmp;}
inline ld S(Point a,Point b){return (ld)(a.y-b.y)/(ld)(a.x-b.x);}
inline ll Pow(ll x){return x*x;}
class Deque{
public:
Point front(){return k[ff];}
Point fnxt(){return k[ff+1];}
Point back(){return k[tt];}
Point bpre(){return k[tt-1];}
bool empty(){return ff>tt;}
bool single(){return ff>=tt;}
void pop_front(){++ff;}
void pop_back(){--tt;}
void push(Point x){k[++tt]=x;}
private:
Point k[N];
int ff=1,tt=0;
};
Deque q;
int main(){
int n;
ll tmp=0,sum=0,L;
Point d;
scanf("%d%lld",&n,&L);
for(int i=1;i<=n;i++)scanf("%lld",&tmp),sum+=tmp,A[i]=sum+i,B[i]=sum+i-1-L;
dp[1]=Pow(A[1]-1-L),q.push(mp(2*A[1],dp[1]+Pow(A[1]),1));
for(int i=2,u;i<=n;i++){
while(!q.empty()&&q.back().x==2*A[i])q.pop_back();
while(!q.single()&&S(q.front(),q.fnxt())-(ld)B[i]<1e-7)q.pop_front();
u=q.front().u;
dp[i]=dp[u]+Pow(B[i])-2*B[i]*A[u]+Pow(A[u]),d=mp(2*A[i],dp[i]+Pow(A[i]),i);
while(!q.single()&&S(q.back(),q.bpre())>S(q.back(),d))q.pop_back();
q.push(d);
}
printf("%lld\n",dp[n]);
return 0;
}
过样例,\(submit\),\(WA\ 0pt\)
我们发现还有一个细节,即任意一个 \(dp\) 有可能由 \(dp[0]\) 转移而来
所以要在一开始插一个虚点
每一道题插虚点的方法都不太一样
本题 \(A[0]=0\) 没有问题
但是 \(dp[0]\) 到底是 \(0\) 还是 \(L^2\) 呢
我们经过思考发现应当是 \(0\)
即表示可以从第一个到第 \(k\) 个都放到一组里
肯定不能在凭空付一个 \(L^2\)
所以插一个虚点 \((0,0)\) 即可
\(AC Code\)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
const int N=50098;
ll dp[N],A[N],B[N];
struct Point{ll x,y;int u;};
//dp[i]=dp[j]+B[i]^2-2B[i]A[j]+A[j]^2=dp[j]-(B[i]-A[j])^2
//dp[j]+A[j]^2=B[i]*2A[j]+(dp[i]-B[i]^2)
//Point(2A[j],dp[j]+A[j]^2)
inline Point mp(ll x,ll y,int u){Point tmp;tmp.x=x,tmp.y=y,tmp.u=u;return tmp;}
inline ld S(Point a,Point b){return (ld)(a.y-b.y)/(ld)(a.x-b.x);}
inline ll Pow(ll x){return x*x;}
class Deque{
public:
Point front(){return k[ff];}
Point fnxt(){return k[ff+1];}
Point back(){return k[tt];}
Point bpre(){return k[tt-1];}
bool empty(){return ff>tt;}
bool single(){return ff>=tt;}
void pop_front(){++ff;}
void pop_back(){--tt;}
void push(Point x){k[++tt]=x;}
private:
Point k[N];
int ff=1,tt=0;
};
Deque q;
int main(){
int n;
ll tmp=0,sum=0,L;
Point d;
scanf("%d%lld",&n,&L);
for(int i=1;i<=n;i++)scanf("%lld",&tmp),sum+=tmp,A[i]=sum+i,B[i]=sum+i-1-L;
q.push(mp(0,0,0));
for(int i=1,u;i<=n;i++){
while(!q.single()&&S(q.front(),q.fnxt())-(ld)B[i]<0)q.pop_front();
u=q.front().u;
dp[i]=dp[u]+Pow(B[i]-A[u]),d=mp(2*A[i],dp[i]+Pow(A[i]),i);
while(!q.empty()&&q.back().x==2*A[i])q.pop_back();
while(!q.single()&&S(q.back(),q.bpre())>S(q.back(),d))q.pop_back();
q.push(d);
}
printf("%lld\n",dp[n]);
return 0;
}
[Example 02 任务安排问题]
题意简述:
机器上有\(N\)个需要处理的任务,它们被分成若干批,每批包含相邻的若干任务。
从时刻\(0\)开始,这些任务被分批加工,第\(i\)个任务单独完成所需的时间是\(T_i\)。
每批任务开始前,机器需要启动时间\(S\),完成这批任务所需时间是各个任务需要时间的总和。
同一批任务将在同一时刻完成。
每个任务的费用是它的完成时刻乘以其费用\(F_i\)。
求最小的总费用。
Basic [ACP3195 任务安排1]
\(1<N<=5000\)
\(0<=S,T_i,C_i<=100\)
Solution
这题有一个点很不好处理
就是费用还和这个完成时刻有关
我们发现完成时刻肯定会加一个前缀和
但是还有若干个 \(S\) (到此为止总共分成了多少组)
思考貌似我们可以记录一个 \(DP[i][j]\) 表示到第 \(i\) 个数总共分成了 \(j\) 组的最小代价
设 \(t\) 是时间的前缀和,\(c\) 是费用的前缀和
然后转移即为
这个转移是 \(O(n^3)\) 的
考虑优化(因为一般斜率优化很少有让你优化二维转移方程的)
算了还是看题解吧
这题里面涉及到了一个思想:部分费用提前计算
啥意思呢?
就是我们在求一个 \(DP\) 值的过程中就提前维护出来这次开机对后面的影响
就是因为我们搞了这一波开机
后面的所有任务都会受影响
与其到后面一个一个的加还不如我提前就整好了
所以新版的 \(DP\) 方程即为
这是一个 \(O(n^2)\) 的转移,通过这题已经够用了
Extra 01[ACP3195 任务安排2]
\(1<N<=300000\)
\(0<=S,T_i,C_i<=512\)
Solution
仿照以前的思路
先去掉 \(min\) 再分组
要求最小化最后一项,仍然是求下凸壳
点的坐标为 \((c[j],dp[j]-S*c[j])\)
斜率为 \(t[i]\)
仍然满足横坐标单调不降和斜率单调不降
可以直接套板子
虚点还是直接插 \((0,0)\) 即可
Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
const int N=300009;
int n,S;
ll dp[N],t[N],c[N];
struct Point{ll x,y;int u;};
inline Point mp(ll x,ll y,int u){Point tmp;tmp.x=x,tmp.y=y,tmp.u=u;return tmp;}
inline ld Slope(Point a,Point b){return (ld)(a.y-b.y)/(ld)(a.x-b.x);}
class Deque{
public:
Point front(){return k[ff];}
Point fnxt(){return k[ff+1];}
Point back(){return k[tt];}
Point bpre(){return k[tt-1];}
bool empty(){return ff>tt;}
bool single(){return ff>=tt;}
void pop_front(){++ff;}
void pop_back(){--tt;}
void push(Point x){k[++tt]=x;}
private:
Point k[N];
int ff=1,tt=0;
}q;
int main(){
int a,b;
Point d;
scanf("%d%d",&n,&S);
for(int i=1;i<=n;i++)scanf("%d%d",&a,&b),t[i]=t[i-1]+a,c[i]=c[i-1]+b;
q.push(mp(0,0,0));
for(int i=1,u;i<=n;i++){
while(!q.single()&&Slope(q.front(),q.fnxt())<t[i])q.pop_front();
u=q.front().u,dp[i]=dp[u]+t[i]*(c[i]-c[u])+S*(c[n]-c[u]),d=mp(c[i],dp[i]-S*c[i],i);
while(!q.empty()&&q.back().x==c[i])q.pop_back();
while(!q.single()&&Slope(q.back(),q.bpre())>Slope(q.back(),d))q.pop_back();
q.push(d);
}
printf("%lld\n",dp[n]);
return 0;
}
Extra 02[ACP3195 任务安排3]
\(1<N<=300000\)
\(0<=S,C_i<=512\)
\(-512<=T_i<=512\)
Solution
这题和以前的唯一区别是斜率不一定单调了
然而这个横坐标仍然是单调的
也就意味着单调队列仍然成立
其中的斜率单调递增,也就意味着统计答案可以直接二分
也不需要 \(pop front\) 了
所以可以把单调队列换成单调栈
虚点什么的都差不多
开干!
Tips:
- 本题如果 \(RP<+10^{10000}\) 的话只用朴素 double Slope 会被卡
需要手动转乘 - 乘负数 MD 要变号!
我也不知道题解咋写的
Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=300007;
struct Point{ll x,y;}k[N];
inline ll cmp(ll a){return (a>0)?1:-1;}
inline ll xx(int a,int b){return k[a].x-k[b].x;}
inline ll yy(int a,int b){return k[a].y-k[b].y;}
ll dp[N],t[N],c[N],S;
int n,st[N],tt=0;
int query(ll val){
int l=1,r=tt-1,mid,ans=tt;
while(l<=r){
mid=(l+r)>>1;
if(yy(st[mid],st[mid+1])*cmp(xx(st[mid],st[mid+1]))>=val*xx(st[mid],st[mid+1])*cmp(xx(st[mid],st[mid+1])))ans=mid,r=mid-1;
else l=mid+1;
}
return st[ans];
}
int main(){
scanf("%d%lld",&n,&S);
for(int i=1;i<=n;i++)scanf("%lld%lld",&t[i],&c[i]),t[i]+=t[i-1],c[i]+=c[i-1];
k[0]={0,0},st[++tt]=0;
for(int i=1,j;i<=n;i++){
j=query(t[i]);
dp[i]=dp[j]+t[i]*c[i]-t[i]*c[j]+S*c[n]-S*c[j];
k[i]={c[i],dp[i]-S*c[i]};
while(tt>0&&k[st[tt]].x==k[i].x&&k[st[tt]].y>=k[i].y)tt--;
while(tt>1&&yy(st[tt],st[tt-1])*xx(st[tt],i)*cmp(xx(st[tt],i)*xx(st[tt],st[tt-1]))>=yy(st[tt],i)*xx(st[tt],st[tt-1])*cmp(xx(st[tt],i)*xx(st[tt],st[tt-1])))tt--;
st[++tt]=i;
}
printf("%lld\n",dp[n]);
return 0;
}
[Example 03 Cats Transport]
有 \(M\) 只猫和 \(P\) 位饲养员。
农场中有一条笔直的路,路边有 \(N\) 座山,第 \(i\) 座山与第 \(i-1\) 座山之间的距离是 \(D_i\) 。饲养员都住在 \(1\) 号山上。
第 \(i\) 只猫去 \(H_i\) 号山玩,玩到时刻 \(T_i\) 停止,然后在原地等饲养员来接。(必须回收所有的猫,不能接到当时仍在玩的猫)
每个饲养员沿着路从 \(1\) 号山走到 \(N\) 号山,把各座山上已经在等待的猫全部接走。饲养员速度为 1 米每单位时间,接猫时间可忽略,可携带为无穷大只猫。
规划每个饲养员从 \(1\) 号山出发的时间,使得所有猫等待时间的总和尽量小。
饲养员出发的时间可以为负。
\(2<=N<=10^5,1<=M<=10^5,1<=P<=100,1<=D_i<=10^4,1<=H_i<=N,0<=T_i<=10^9\)
Solution
首先有一个很显然的简化
在后面的猫玩耍时间可以同减去它到一号山的距离
这样接猫的时候就不需要考虑奇奇怪怪的行走问题了
接下来我们发现问题转变成了:
把一个数列分成若干组(斜优狂喜)
定义每一组的代价是组内最大值减去组内所有数差值之和
我们发现这数列的顺序不重要
那我们可以升序排序
这样就变成了一个数列分成若干段,每段代价是 \(Sum-Len*Max\),其中 \(Max\) 其实就是第后一个元素
但有一个问题
就是饲养员是有限个的!
设 \(dp[i][j]\) 为前 \(i\) 个元素用 \(j\) 个饲养员的最小代价
设 \(k[i]\) 为第 \(i\) 个元素按照上文所说得到的值
设 \(sum[i]\) 为 \(k\) 数组前 \(i\) 个元素的和
则有如下转移
一脸懵逼的我看了题解发现确实是二维的 DP
这个转移是 \(O(N^2*P)\) 的
套个斜优 \(O(N*P)\) 就能过
化简下
坐标 \(j,dp[j][p-1]+sum[j]\) 斜率 \(k[i]\)
虚点直接插 \((0,0)\)
两边不降直接开干!
Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
const int Size=100003;
struct Point{ll x,y;int u;}a[Size],tmp;
inline ld S(Point a,Point b){return (a.x==b.x)?1e50:(ld)(a.y-b.y)/(a.x-b.x);}
int N,M,P,Dist[Size],ff=1,tt=0;
long long sum[Size],k[Size],dp[Size],mem[Size];
int main(){
int p,t;
scanf("%d%d%d",&N,&M,&P);
if(P>M)puts("0"),exit(0);
for(int i=2;i<=N;i++)scanf("%d",&Dist[i]),Dist[i]+=Dist[i-1];
for(int i=1;i<=M;i++)scanf("%d%d",&p,&t),k[i]=t-Dist[p];
sort(k+1,k+M+1);
for(int i=1;i<=M;i++)sum[i]=sum[i-1]+k[i],mem[i]=1e17,dp[i]=1e17;
for(int num=1;num<=P;num++){
ff=1,tt=0,a[++tt]={0,0,0};
//printf("Round %d\n",num);
for(int i=1,j;i<=M;i++){
while(ff<tt&&S(a[ff],a[ff+1])-(ld)k[i]<0)++ff;
j=a[ff].u,dp[i]=mem[j]+(i-j)*k[i]-(sum[i]-sum[j]);
//printf("dp[%d]=%lld\n",i,dp[i]);
tmp={i,mem[i]+sum[i],i};
while(ff<tt&&S(a[tt],a[tt-1])>S(a[tt],tmp))--tt;
a[++tt]=tmp;
}
for(int i=1;i<=M;i++)mem[i]=dp[i];
}
printf("%lld\n",dp[M]);
return 0;
}
[Example 04 仓库建设]
L 公司有 \(n\) 个工厂,由高到低分布在一座山上,工厂 \(1\) 在山顶,工厂 \(n\) 在山脚。
由于这座山处于高原内陆地区(干燥少雨),L公司一般把产品直接堆放在露天,以节省费用。突然有一天,L 公司的总裁 L 先生接到气象部门的电话,被告知三天之后将有一场暴雨,于是 L 先生决定紧急在某些工厂建立一些仓库以免产品被淋坏。
由于地形的不同,在不同工厂建立仓库的费用可能是不同的。第 \(i\) 个工厂目前已有成品 \(p_i\) 件,在第 \(i\) 个工厂位置建立仓库的费用是 \(c_i\)。
对于没有建立仓库的工厂,其产品应被运往其他的仓库进行储藏,而由于 L 公司产品的对外销售处设置在山脚的工厂 \(n\),故产品只能往山下运(即只能运往编号更大的工厂的仓库),当然运送产品也是需要费用的,一件产品运送一个单位距离的费用是 \(1\)。
假设建立的仓库容量都都是足够大的,可以容下所有的产品。你将得到以下数据:
- 工厂 \(i\) 距离工厂 \(1\) 的距离 \(x_i\)(其中 \(x_1=0\))。
- 工厂 \(i\) 目前已有成品数量 \(p_i\)。
- 在工厂 \(i\) 建立仓库的费用 \(c_i\)。
请你帮助 L 公司寻找一个仓库建设的方案,使得总的费用最小。
Solution
相当水的题,基本就是模板
设 \(sumC\) 为 \(cnt\) 前缀和
设 \(Fuck\) 为 \(Dis[i]+cnt[i]\) 前缀和
点坐标 \((sumC[i],dp[i]+Fuck[i])\) 斜率 \(Dis[i]\)
双单增直接板子
Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
const int N=1000003;
int n,q[N],ff=1,tt=0;
long long dis[N],cost[N],sumc[N],fuck[N],tmp,dp[N];
inline ld S(int a,int b){return (sumc[a]==sumc[b])?1e50:(ld)(dp[a]+fuck[a]-dp[b]-fuck[b])/(sumc[a]-sumc[b]);}
int main(){
scanf("%d",&n),q[++tt]=0;
for(int i=1;i<=n;i++)scanf("%lld%lld%lld",&dis[i],&tmp,&cost[i]),sumc[i]=sumc[i-1]+tmp,fuck[i]=fuck[i-1]+dis[i]*tmp;
for(int i=1,j;i<=n;i++){
while(ff<tt&&S(q[ff],q[ff+1])-(ld)dis[i]<0)++ff;
j=q[ff],dp[i]=dp[j]+cost[i]+dis[i]*(sumc[i-1]-sumc[j])-(fuck[i-1]-fuck[j]);
while(ff<tt&&S(q[tt-1],q[tt])>S(q[tt],i))--tt;
q[++tt]=i;
}
printf("%lld",dp[n]);
return 0;
}
但该代码会被 luogu 的题 Hack 掉
原因是是要去掉最后几个没有货物的仓库
在一通乱搞得到 \(AC\ Code\)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
const int N=1000003;
int n,q[N],ff=1,tt=0;
long long dis[N],cost[N],sumc[N],fuck[N],tmp,dp[N];
inline ld S(int a,int b){return (sumc[a]==sumc[b])?1e50:(ld)(dp[a]+fuck[a]-dp[b]-fuck[b])/(sumc[a]-sumc[b]);}
int main(){
scanf("%d",&n),q[++tt]=0;
for(int i=1;i<=n;i++)scanf("%lld%lld%lld",&dis[i],&tmp,&cost[i]),sumc[i]=sumc[i-1]+tmp,fuck[i]=fuck[i-1]+dis[i]*tmp;
for(int i=1,j;i<=n;i++){
while(ff<tt&&S(q[ff],q[ff+1])-(ld)dis[i]<0)++ff;
j=q[ff],dp[i]=dp[j]+cost[i]+dis[i]*(sumc[i-1]-sumc[j])-(fuck[i-1]-fuck[j]);
while(ff<=tt&&sumc[q[tt]]==sumc[i]&&dp[q[tt]]+fuck[q[tt]]>=dp[i]+fuck[i])--tt;
while(ff<tt&&S(q[tt-1],q[tt])-S(q[tt],i)>0)--tt;
q[++tt]=i;
}
for(int i=n-1;i>=1;i--)if(sumc[n]-sumc[i]==0)dp[n]=min(dp[n],dp[i]);else break;
printf("%lld",dp[n]);
return 0;
}
[Example 05 特别行动队]
纯模板唐氏题
APIO 就这?
坐标 \((sum[j],dp[j]+a*sum[j]^2-b*sum[j])\)
斜率 \(2*a*sum[i]\)
但问题就在这里
MD \(-5<=a<=-1\)
但你突然发现这 TM 是一个上凸壳(max)
上凸壳的斜率单调不升
所以我们当前斜率大于当前线段时一定可排除以前的所有线段
所以,还是板子
Warning: rt,这里的 a 必须乘进 Slope
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
const int N=1e6+7;
int n,q[N],ff=1,tt=0;
ll a,b,c,sum[N],tmp,dp[N];
inline ld S(int aa,int bb){return (ld)(dp[aa]+a*sum[aa]*sum[aa]-b*sum[aa]-dp[bb]-a*sum[bb]*sum[bb]+b*sum[bb])/(sum[aa]-sum[bb]);}
int main(){
scanf("%d%lld%lld%lld",&n,&a,&b,&c),q[++tt]=0;
for(int i=1;i<=n;i++)scanf("%lld",&tmp),sum[i]=sum[i-1]+tmp;
for(int i=1,j;i<=n;i++){
while(ff<tt&&S(q[ff],q[ff+1])>2.0*a*sum[i])ff++;
j=q[ff],dp[i]=dp[j]+a*(sum[i]-sum[j])*(sum[i]-sum[j])+b*(sum[i]-sum[j])+c;
while(ff<tt&&S(q[tt-1],q[tt])<S(q[tt],i))--tt;
q[++tt]=i;
}
printf("%lld\n",dp[n]);
return 0;
}
[Example 06 打印文章]
纯模板唐氏题*2
point \(sum[j],dp[j]+sum[j]^2\)
slope \(2*sum[i]\)
注意多测
Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
const int N=500009;
int n,q[N],ff=1,tt=1;
ll sum[N],dp[N],M,tmp;
inline ld S(int a,int b){return (sum[a]==sum[b])?1e50:(dp[a]-dp[b]+sum[a]*sum[a]-sum[b]*sum[b])/(sum[a]-sum[b]);}
int main(){
while(scanf("%d%lld",&n,&M)!=EOF){
ff=1,tt=1;
for(int i=1;i<=n;i++)scanf("%lld",&tmp),sum[i]=sum[i-1]+tmp;
for(int i=1,j;i<=n;i++){
while(ff<tt&&S(q[ff],q[ff+1])-(ld)2*sum[i]<0)++ff;
j=q[ff],dp[i]=dp[j]+M+(sum[i]-sum[j])*(sum[i]-sum[j]);
while(ff<tt&&S(q[tt],q[tt-1])>S(q[tt],i))--tt;
q[++tt]=i;
}
printf("%lld\n",dp[n]);
}
return 0;
}
[Final 锯木厂选址]
这次终于不是唐氏题目了
数列分三段。。。貌似是 Cat 弱化版 + 仓库建设思想
笑死,还是唐氏题
在推一次
维护每个点到山脚的距离 \(dis\)
设 \(sum\) 为 \(w\) 的前缀和, \(shit\) 为 \(dis[i]*w[i]\) 的前缀和
point \(sum[j],dp[j][num-1]-shit[j]\)
slope \(-dis[i]\)
Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
const int N=200009;
int n,q[N],ff=1,tt=1;
ll dis[N],sum[N],shit[N],tmp,dp[N],mem[N];
inline ld S(int a,int b){return (ld)(mem[a]-shit[a]-mem[b]+shit[b])/(sum[a]-sum[b]);}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%lld%lld",&sum[i],&dis[i]);
for(int i=n;i>=1;i--)dis[i]+=dis[i+1],shit[i]=dis[i]*sum[i];
for(int i=1;i<=n;i++)shit[i]+=shit[i-1],sum[i]+=sum[i-1],dp[i]=mem[i]=1e16;
++n,dis[n]=0,sum[n]=sum[n-1]+1,shit[n]=shit[n-1],mem[n]=dp[n]=1e16;
for(int num=1;num<=3;num++){
ff=1,tt=1;
//printf("Round %d\n",num);
for(int i=1,j;i<=n;i++){
while(ff<tt&&S(q[ff],q[ff+1])+(ld)dis[i]<0)++ff;
j=q[ff],dp[i]=mem[j]+shit[i]-shit[j]-(sum[i]-sum[j])*dis[i];
//printf("DP[%d]=%lld from %d\n",i,dp[i],j);
while(ff<tt&&S(q[tt],q[tt-1])>S(q[tt],i))--tt;
q[++tt]=i;
}
for(int i=1;i<=n;i++)mem[i]=dp[i];
}
printf("%lld\n",dp[n]);
return 0;
}
以下就没有了
有好题可直接 @蒟蒻作者 更新
拜拜




 浙公网安备 33010602011771号
浙公网安备 33010602011771号