P1282 多米诺骨牌

链接

https://www.luogu.com.cn/problem/P1282

思路

本来的思路是dp[i][j][0/1]表示前i个选j个翻面其中第i个是（1）否（0）翻面。然后递推取min。但是这样很显然会导致类似贪心的问题：只符合前面的局部利益，不符合后续最佳组合。
正确做法：
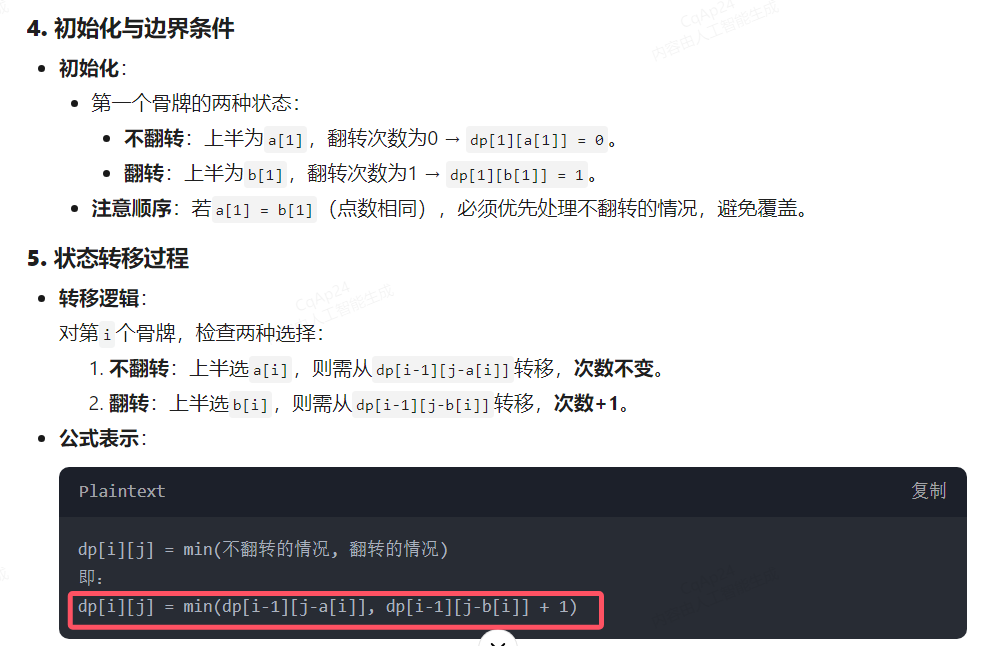
用dp[i][j]来表示当前考虑到第i个骨牌，第一行的总和为j的最小交换次数。记第一行骨牌的点数放入数组a，第二行骨牌的点数放入数组b，初始时令dp[1][a[1]]=0，dp[1][b[1]]=1。
状态转移方程为：dp[i][j]=min(dp[i][j],dp[i-1][j-a[i]])
dp[i][j]=min(dp[i][j],dp[i-1][j-b[i]]+1)
由于我们可以计算所有牌的总和，最终，再从所有的能通过交换使得第一行的所有总和中，找到使差值最小的。

代码

#include<bits/stdc++.h>
using namespace std;
const int inf=1e9;
int n;
int a[1007],b[1007];
int dp[1007][6007];
int sum;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&a[i],&b[i]);
        sum+=a[i]+b[i];
    }
    for (int i = 1; i <= n; i ++)
    for (int j = 0; j <= 6*n; j ++) dp[i][j] = inf;
    dp[1][b[1]]=1,dp[1][a[1]]=0;//这个顺序不能交换，因为当第一个牌相等时，一二行不用换
    for(int i=2;i<=n;i++)
    for(int j=0;j<=6*i;j++)
    {
        if(j-a[i]>=0) dp[i][j]=min(dp[i][j],dp[i-1][j-a[i]]);
        if(j-b[i]>=0) dp[i][j]=min(dp[i][j],dp[i-1][j-b[i]]+1);
    }
    int mi=inf,ans=inf;
    for(int i=0;i<=sum;i++)
    {
        if(dp[n][i]!=inf){
        if(abs(sum-2*i)<mi)
        {
            ans=dp[n][i];
            mi=abs(sum-2*i);
        }
        else if(abs(sum-2*i)==mi)
        {
            ans=min(ans,dp[n][i]);
        }
        }
    }
    printf("%d\n",ans);
    return 0;
}