梯度提升决策树公式推导

梯度提升决策树(GBDT,Gradient Boosting Decision Tree)

梯度提升算法使用损失函数的负梯度在当前模型的值，
不再去学习残差，而是学习一个损失函数关于梯度的负值。

\[\begin{equation}\begin{split} -\left[\frac {\partial L(y,f(x_i))}{\partial f(x_i)}\right]_{f(x)=f_{m-1}(x)} \end{split}\end{equation} \]

作为回归问题提升决策树算法中残差的近似值，拟合一个回归树。
如果xgboost在这里改进的话可以采用二阶梯度，因为一个函数泰勒展开项阶数越高精度约大。(xgboost第一个改进)

为什么用负梯度？

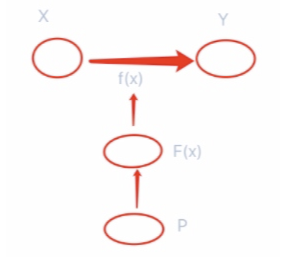
首先我们要学习的是从输入空间x到输出空间y的一个映射f。
因为这样的f有很多个，所以构建一个F叫假设空间。
要在假设空间F中找一个\(f*\)最优的映射。
f的最终表示可以用w和b这种权重和偏置来表示。
所以最终的学习，是学习使损失函数最小的参数的问题。
所以除了F假设空间外，还有个P空间，也就是参数空间。
在参数空间找w和b，由最优w和b去确定f，由f去完成映射。
而最优参数\(w*\) 如何学习，就是由
\(\begin{equation}\begin{split} \frac {\partial f(w)}{\partial w}=0 \end{split}\end{equation}\) 求得 \(w*\)
\(w*\)如何求得？
\(w^* =arg\min L(w)\)
就是由 \(w-\alpha\frac {\partial f(w)}{\partial w}\) 迭代求得，也就是梯度下降法。
也就是在参数空间下来做的。
那么能不能直接在假设空间F上来做？
\(F^w = arg\min L(f) \\ \frac {\partial L(f)}{\partial f}=0\\ f=f-\beta\frac {\partial L(f)}{\partial f} ,\beta=1\)

那么没有了参数，函数如何表示？

\[\begin{equation}\begin{split} T(x;\Theta) = \sum_{j=1}^j c_jI(x\in R_j) \end{split}\end{equation} \]

还是决策树的本质问题，把输入空间划分为不同的离散区域，确定每个区域的输出值。这样直接对一棵树进行学习就好了。

梯度提升算法过程：

• 输入:训练数据集 \(T=\lbrace(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\rbrace\)

• 输出：梯度提升决策树\(\hat f(x)\)
  (1)初始化

  \[\begin{equation}\begin{split} f_0(x)=arg\min_c\sum_{i=1}^NL(y_i,c) \end{split}\end{equation} \]

  (2) 对 \(m=1,2,...,M\)

  • (a) 对 \(i=1,2,...,N\) 计算
    \[ r_{mi} = -\left[\frac {\partial L(y,f(x_i))}{\partial f(x_i)}\right]_{f(x)=f_{m-1}(x)} \]

  • (b) 对\(r_mi\)拟合一个回归树，得到第m颗树的叶节点区域 \(R_{mj},j=1,2,...,J\)
  • (c) 对 \(R_{mj},j=1,2,...,J\)，计算
    \[c_{mj}=arg\min_c\sum_{x\in R_{mj}}L(y_i,f_{m-1}(x_i)+c) \]

  这个地方也是将来xgboost要改进的点。经验风险最小化容易导致过拟合，可以采用正则化项。(xgboost第二个改进)

  • (d) 更新\(f_m(x)=f_{m-1}(x)+\sum_{j=1}^J c_{mj}I(x \in R_{mj})\)

  (3)得到回归梯度提升决策树

  \[\begin{equation}\begin{split} \hat f(x)=f_M(x)=\sum_{m=1}^M\sum_{j=1}^Jc_{mj}I(x \in R_{mj}) \end{split}\end{equation} \]