BP神经网络笔记_1

这是第一篇神经网络的笔记，希望能够坚持写下去。这个笔记的内容主要是吴恩达机器学习视频中的内容，为了方便本人的理解，才有了这篇笔记。

两层

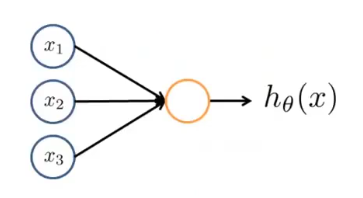
这是一个两层神经网络模型，只含有输入层和输出层，没有隐含层。

我们来看最简单的，似逻辑回归里的情况，\(x_1, x_2, x_3\)全为实数，并且我们添加一个恒为1的\(x_0\)，则可设

\[x = [x_0,x_1,x_2, x_3]^T \]

\[\theta = [\theta_0, \theta_1, \theta_2, \theta_3]^T \]

我们选择sigmoid函数为

\[g(\theta^Tx) = 1/{(1+e^{-\theta^Tx})} \]

则当\(\theta\)确定时

\[h_\theta(x) = g(\theta^Tx) \]

若我们对其扩展，设有\(n\)个变量，且\(x_1, x_2,\dots, x_n\)全为\(m\)维向量，则\(x_0\)也为\(m\)维向量，则\(x\)为\(n+1 \times m\)矩阵

\[x = \left[ \begin{matrix} x_0^1 & x_0^2 & \cdots & x_0^m\\ x_1^1 & x_1^2 & \cdots & x_1^m\\ \vdots& \vdots& \ddots & \vdots\\ x_n^1 & x_n^2 & \cdots & x_n^m \end{matrix} \right] = \left[ \begin{matrix} x_0\\ x_1\\ \vdots\\ x_n \end{matrix} \right] \]

同时\(\theta\)为一个\(n+1\)维列向量

\[\theta = \left[ \begin{matrix} \theta_0\\ \theta_1\\ \vdots\\ \theta_n \end{matrix} \right] \]

则\(\theta^Tx\)为一个\(m\)维行向量

\[\theta^Tx= \left[ \begin{matrix} \theta_0x_0^1 + \theta_0x_0^2 + \cdots+\theta_0x_0^m\\ \theta_1x_1^1 + \theta_1x_1^2 + \cdots + \theta_1x_1^m\\ \vdots\\ \theta_nx_n^1 + \theta_nx_n^2 + \cdots + \theta_nx_n^m\\ \end{matrix} \right]^T \]

则

\[g(\theta^Tx) = g(\left[ \begin{matrix} \theta_0x_0^1 + \theta_0x_0^2 + \cdots+\theta_0x_0^m\\ \theta_1x_1^1 + \theta_1x_1^2 + \cdots + \theta_1x_1^m\\ \vdots\\ \theta_nx_n^1 + \theta_nx_n^2 + \cdots + \theta_nx_n^m\\ \end{matrix} \right]^T) = h_\theta(x) \]

我们得到了一个\(m\)维的结果行向量

三层

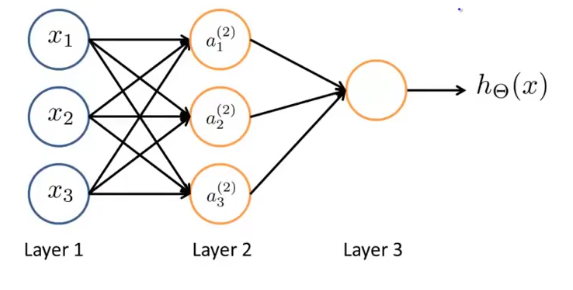
有了上面两层神经网络的认识，我们现在来看三层的神经网络

我们先单独分析\(a_1\)，对\(a_1\)来说，其原理即为上述两层神经网络模型。我们可以设layer1对\(a_1\)的参数为\(\theta_1\)，则\(\theta_1\)为4维列向量，\(x\)为\(4\times m\)矩阵

\[\theta_1 = \left[ \begin{matrix} \theta_1^0\\ \theta_1^1\\ \theta_1^2\\ \theta_1^3 \end{matrix} \right] \]

\[x = \left[ \begin{matrix} x_0^1 & x_0^2 & \cdots & x_0^m\\ x_1^1 & x_1^2 & \cdots & x_1^m\\ x_2^1 & x_2^2 & \cdots & x_2^m\\ x_3^1 & x_3^2 & \cdots & x_3^m \end{matrix} \right] \]

所以对于\(a_1\)来说，\(a_1\)为\(m\)维行向量

\[a_1 = h_{\theta_1}(x) = g(\theta_1^Tx) \]

同理

\[a_2 = h_{\theta_2}(x) = g(\theta_2^Tx) \]

所以我们可以将\(\theta_1, \theta_2, \theta_3\)组合起来，构成一个矩阵\(\Theta_1\)，则

\[\Theta_1 = \left[ \begin{matrix} \theta_1 & \theta_2 & \theta_3 \end{matrix} \right] = \left[ \begin{matrix} \theta_1^0 & \theta_2^0 & \theta_3^0\\ \theta_1^1 & \theta_2^1 & \theta_3^1\\ \theta_1^2 & \theta_2^2 & \theta_3^2\\ \theta_1^3 & \theta_2^3 & \theta_3^3 \end{matrix} \right] \]

\[\Theta_1^Tx = \left[ \begin{matrix} \theta_1^0x_0^1+\theta_1^1x_1^1+\theta_1^2x_2^1+\theta_1^3x_3^1 & \theta_1^0x_0^2+\theta_1^1x_1^2+\theta_1^2x_2^2+\theta_1^3x_3^2 & \cdots & \theta_1^0x_0^m+\theta_1^1x_1^m+\theta_1^2x_2^m+\theta_1^3x_3^m \\ \theta_2^0x_0^1+\theta_2^1x_1^1+\theta_2^2x_2^1+\theta_2^3x_3^1 & \theta_2^0x_0^2+\theta_2^1x_1^2+\theta_2^2x_2^2+\theta_2^3x_3^2 & \cdots & \theta_2^0x_0^m+\theta_2^1x_1^m+\theta_2^2x_2^m+\theta_2^3x_3^m \\ \theta_3^0x_0^1+\theta_3^1x_1^1+\theta_3^2x_2^1+\theta_3^3x_3^1 & \theta_3^0x_0^2+\theta_3^1x_1^2+\theta_3^2x_2^2+\theta_3^3x_3^2 & \cdots & \theta_3^0x_0^m+\theta_3^1x_1^m+\theta_3^2x_2^m+\theta_3^3x_3^m \\ \end{matrix} \right] \]

我们另

\[a = h_{\Theta_1}(x) = g(\Theta_1^Tx) \]

则\(a\)为\(3\times\) m矩阵，同时我们对\(a\)进行扩充，加入一恒为1的\(m\)维行向量，则\(a\)为\(4\times m\)矩阵

\[a = \left[ \begin{matrix} a_0^1 & a_0^2 & \cdots & a_0^m\\ a_1^1 & a_1^2 & \cdots & a_1^m\\ a_2^1 & a_2^2 & \cdots & a_2^m\\ a_3^1 & a_3^2 & \cdots & a_3^m\\ \end{matrix} \right] \]

同时我们对layer2与layer3进行分析，发现也为二层神经网络模型，于是套用公式，设\(\Theta_2\)，由于layer3只有一个节点，所以

注：此时的\(\theta_1\)与上面的layer1的\(\theta_1\)不同，是layer2的参数

\[\Theta_2 = \theta_1 = \left[ \begin{matrix} \theta_1^0\\ \theta_1^1\\ \theta_1^2\\ \theta_1^3 \end{matrix} \right] \]

最后我们得到

\[y = h_{\Theta_2}(a) = g(\Theta_2^Ta) \]

结果\(y\)为\(m\)维行向量

若layer3含有\(k\)个输出节点，则我们可对上面式子进行扩展

\[\Theta_2 = \left[ \begin{matrix} \theta_1 & \theta_2 & \cdots & \theta_k \end{matrix} \right] = \left[ \begin{matrix} \theta_1^0 & \theta_2^0 & \cdots & \theta_k^0\\ \theta_1^1 & \theta_2^1 & \cdots & \theta_k^1\\ \theta_1^2 & \theta_2^2 & \cdots & \theta_k^2\\ \theta_1^3 & \theta_2^3 & \cdots & \theta_k^3 \end{matrix} \right] \]

所以\(\Theta_2^Ta\)为\(k\times m\)矩阵，所以我们得到的\(y=h_{\Theta_2}(a)=g(\Theta_2^Ta)\)为\(k\times m\)矩阵