数独sudoku(二)软件设计
大家好,今天进入设计阶段,分概要设计和详细设计两部分。
Github完整项目地址:https://github.com/surpasss/software-engineering
1.概要设计
概要设计在这道题中主要是划分模块。我们上期讲到两个子任务,生成终局和求解数独,生成数独命令行传入sudoku.exe -c n,求解数独命令行传入sudoku.exe -s path,因此在主函数需要根据传入的第二个参数是"-c"还是"-s"选择调用对应的模块,这里的模块可以理解为源文件.cpp. 出于模块划分的高内聚低耦合的要求,应该尽量减少模块间的数据传递、禁止数据共享,这两个子任务肯定是分模块处理,很容易想到传递的参数是n和path,而不是不传参数导致共享数据、或者传递过多参数不利于信息隐藏,至于具体的操作就在模块中封闭处理。 在此给出概要设计阶段的函数调用图:
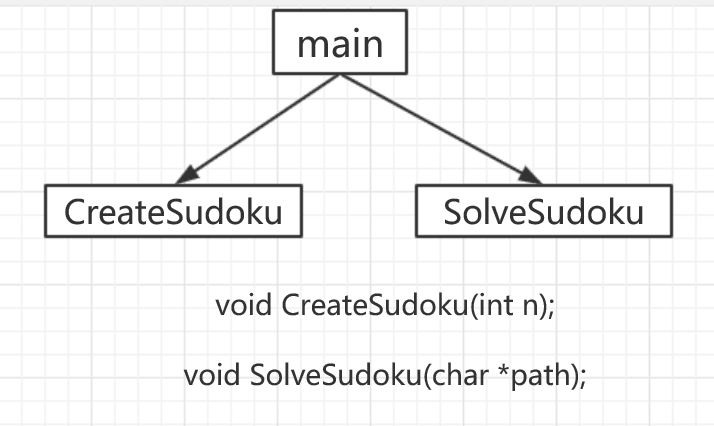
2. 详细设计
详细设计是在概要设计的基础上,具体实现各部分的细节,使得编码的任务就是讲详细设计的内容“翻译”成程序设计语言。详细设计阶段就是从编码的角度回答“如何实现”,所以现在就要具体剖析问题、寻找解决方案了。
2.1 如何生成终局
#######首先来看一个合法的数独终局:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
| 7 | 8 | 9 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 5 | 6 | 7 | 8 | 9 | 1 | 2 | 3 |
| 9 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 6 | 7 | 8 | 9 | 1 | 2 | 3 | 4 | 5 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 | 2 |
| 8 | 9 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 6 | 7 | 8 | 9 | 1 | 2 | 3 | 4 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 |
| 可以发现,对于这个数独终局,从第2行开始,每行分别是第1行右移3、6、1、4、7、2、5、8列的结果。显然,对于任何一个1~9的全排列,都可以通过这种方式得到一个终局,这样就可以获得9!= 362880种终局。但是题目要求左上角的数字是学号后两位之和mod 9 + 1,这样就只有8!= 40320种终局。 | ||||||||
| 并且还可以发现,对于任何一个数独终局的13行,任意交换这三行的顺序,得到的仍然是一个合法的终局。同理,任意交换46行、79行的顺序也可以,任意交换13列,46列,79列仍然满足(但是交换列之后得到的数独可能会重复,因为第1行已经不唯一了)。此外,把棋盘分成13行、46行、7~9行这三块,任意交换这三块的顺序得到的终局仍是合法的,列也同理合法。当然,还有很多其他规律。 | ||||||||
| 这样一来,得到的终局就非常多了。因为左上角的数字是固定的,为了简单起见,可以任意交换46行的顺序、79行的顺序,得到的终局数量则有40320×3!×3!= 1451520种,已经超过了1e6。 | ||||||||
| 前面三段我是不加解释地直接给出生成1e6个终局的方法,而题目中要求这些数独是合理的数独且不重复,接下来我来详细分析下上述方法的可行性。 | ||||||||
| 首先是把第1行的19全排列右移0、3、6、1、4、7、2、5、8列得到的9×9数组为什么是个合理的数独,即每一行、每一列、每个3×3方格都包含19这9个数字。因为后面每行的数字都是由第1行的9个不同数字平移得到,所以可以保证每一行都包含19;对于同一列的数字,也是由第1行的不同数字平移得到,因为0、3、6、1、4、7、2、5、8组成08、且不重复,因此可以保证每一列都包含1~9;而对于9个3×3方格,同样来自第1行的9个不同数字。以左上角的方格为例,第2行的前三个数字是由第1行的最后三个数字平移得到,第3行的前三个数字是由第1行的中间三个数字平移得到,而这9个数字正好构成第1行的9个不同数字。这是因为0、3、6、0挨着的两个数字之间的距离为3,所以第2行、第3行的前三个数字来源于第1行的不同位置,同理可推广到其他3×3方格。 | ||||||||
| 其次是为什么这样生成的每个数独不重复呢,首先每3!×3!= 36个数独的第一行都不同,所以先把范围缩小为36个第一行相同的数独。这36个数独的前三行都相同,46行是平移1、4、7的全排列,79行是平移2、5、8的全排列,同样继续分解得到这36个数独皆不相同。 | ||||||||
| 前面已经分析完方法和合理性,接下来分析如何编程实现。首先是得到19全排列作为第1行,第1行平移不同单位得到28行,如此循环,直到达到要求的数量。因为有循环,所以可以添加一个平移函数完成平移生成终局,那应该怎么传参呢?我个人觉得,同一个源文件中的不同函数之间应该减小函数接口的复杂度,即采用数据耦合且参数数量少,这并不意味着在不同函数内部修改全局变量,但可以共享,即函数可以共用全局变量,但只有一个函数可以修改全局变量,这是可以做到的。当然,这是在函数结构比较简单的情况下,具体问题还应该具体分析,凡事都有利弊。所以可以事先定义三个平移数组,分别对应每3行的右移单位,定义伪代码如下: |
//均通过第1行的各列右移,4-6行、7-9行各6次变换
int row_trans_0[3] = { 0, 3, 6 };//1-3行的右移列数
int row_trans_1[6][3] = { {1, 4, 7}, {1, 7, 4}, {4, 1, 7}, {4, 7, 1}, {7, 1, 4}, {7, 4, 1} };//4-6行的右移列数
int row_trans_2[6][3] = { {2, 5, 8}, {2, 8, 5}, {5, 2, 8}, {5, 8, 2}, {8, 2, 5}, {8, 5, 2} };//7-9行的右移列数
因此平移函数只需要传递两个整型参数,分别对应row_trans_1的第一维位置和row_trans_2的第一维位置。之后在平移函数中生成一个终局,写入sudoku.txt文件中,如此循环即可。此处另外一个问题是如何生成1~9的全排列作为第1行,这可以通过调用STL库的next_permutation函数实现,next_permutation函数是按照数组当前字典序产生全排列,因此保证每次调用后的数组不重复,详情可看此链接[next_permutation用法]。还有个问题是如何将生成的终局写入文件中,可以在平移函数中每生成一个终局就打开文件写入文件关闭文件,减弱与调用函数的耦合度。
这里补充一点,题目中要求终局之间有一行空行,最后一个终局后无空行。所以平移函数的传参还需要增加一个判断变量flag,如果是最后一个终局,在文件中不加换行符,否则添加换行符,之前生成的每个终局用二维整型数组暂存即可。
2.2 如何求解数独
题目中要求对每个残局找到一个可行解,所以很显然可以考虑用深度优先搜索的方法解决。每次从文件中读出一个残局,用二维整型数组保存好。 然后进入DFS递归函数遍历每个位置,传入的参数应该是n(0≦n≦80),对每个尚未填充数字的位置依次检查是否可以填充1~9,如果可以则先填充,继续深搜,如果都不能填充则回溯。直到深搜到最后一个位置,将数组写入sudoku.txt文件中,然后层层回退。
此处另外一个问题是如何检查该位置是否可以填充19中的某个数字呢,如果可以填充,则需要满足该位置所在的行、列、3×3方格均无该数字。但是如果这样检查的话,对每个数字最多需要访问27次数组,无疑很费时,所以可以用一个三维数组occupy[3][10][10]保存每一行、每一列、每个方格的19这9个数字是否存在。第一维表示行或列或小方格,第二维表示行或列或小方格的序号,第三维表示数字1~9,如果已存在,则对应值为1。这样的话,对每个数字就只需要访问3次数组即可。
还有个小问题是每个位置(0≦n≦80)所在的行和列很好判断,但是如何判断所在方格呢?这可以通过推导公式,但是一番思考后我觉得更直接的方法是用一个全局数组保存好每个位置所在的方格序号,之后直接访问即可。相比于推导公式,这样代码可读性也更好,虽然可能增大点开销。
至此,详细设计阶段的分析任务已经完成了,思路应该比较清晰了。因为函数比较简单,所以函数内部的具体实现就留到编码阶段。下面给出详细设计阶段的函数调用图(注:箭头指向表示调用顺序):
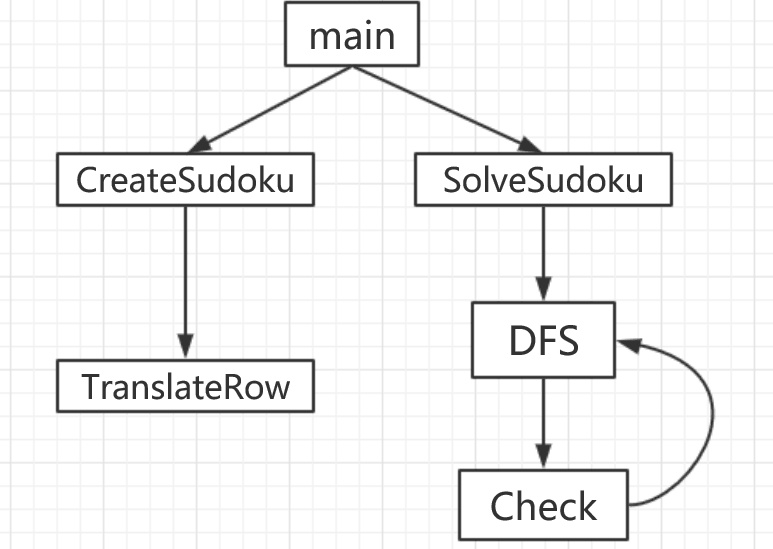
函数声明为:
void CreateSudoku(int n);//n为需生成终局的数量
void TranslateRow(int trans_1, int trans_2, bool flag);
//trans_1为row_trans_1的第一维位置,trans_2为row_trans_2的第一维位置, flag表示是否是最后一个终局
void SolveSudoku (char *path);//path为残局文件的路径
void DFS(int n);//n为小格子的序号(0-80)
bool Check(int n, int key);//n为小格子的序号(0-80),key为是否填充该小格子的数字(1-9)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号