狄利克雷卷积
在算术函数集上,可以定义一种二元运算,使得取这种运算为乘法,取普通函数加法为加法,使得算术函数集为一个交换环。其中一种这样的运算便是狄利克雷卷积。它和一般的卷积有不少相类之处。
对于算术函数 ,定义其狄利克雷卷积
,定义其狄利克雷卷积 。
。
运算[编辑]
 的值如下:
的值如下:
![f^{-1}(1)= \frac{1}{f(1)}]()
- 对于
![n>1]() ,
,![f^{-1}(n)= \frac{-1}{f(1)} \sum_{d|n , n \ne d} f(\frac{n}{d}) f^{-1}(d)]()
默比乌斯函数μ的逆函数为(一般意义上的)1,即对于 ,
,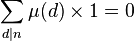 。这是默比乌斯反转公式的原理。
。这是默比乌斯反转公式的原理。
狄利克雷卷积以数学家狄利克雷命名。1857年刘维尔曾发表了许多包含这个运算的恒等式。将它视为二元运算这个观点是E. T. 贝尔和 M. Cipolla 在1915年提出的。
导数[编辑]
若定义 的“导数”
的“导数” ,可以发现这个运算和连续实函数的导数有不少相似的地方:
,可以发现这个运算和连续实函数的导数有不少相似的地方:
级数[编辑]
对于算术函数f,定义其狄利克雷级数
对于一些算术函数的狄利克雷级数,它们的积,跟那些算术函数的狄利克雷卷积的狄利克雷级数是相等的:
这跟卷积定理很相似。
定义f的贝尔级数
也有类似的关系:
参考[编辑]
- Introduction to Analytic Number theory, Tom M. Apostol
- http://eom.springer.de/D/d130150.htm


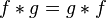


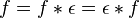 。ε(n)的值为1若n=1,否则ε(n)=0。
。ε(n)的值为1若n=1,否则ε(n)=0。 不等于0,都有唯一的
不等于0,都有唯一的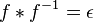 。
。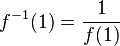
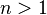 ,
,
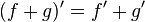

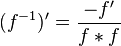
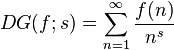

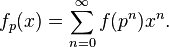
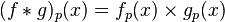

 浙公网安备 33010602011771号
浙公网安备 33010602011771号