笛卡尔树学习笔记

笛卡尔树 - OI-wiki

笛卡尔树是一个看起来功能类似于单调栈的东西，对于一个序列构建笛卡尔树的时空复杂度均为 \(O(n)\)。

具体地，笛卡尔树（Cartesian Tree）是一个二叉树，其中的每个节点都维护有两个键值 \(k\) 和 \(w\)。同时，\(k\) 在笛卡尔树上满足二叉搜索树的性质，\(w\) 在笛卡尔树上满足堆的性质。

我们容易得出结论：若 \(k\) 互不相同，\(w\) 也互不相同，则笛卡尔树的形态固定。

笛卡尔树的构建

考虑对于一个序列，以其下标为 \(k\)，权值为 \(w\) 构建笛卡尔树。按照下标顺序依次插入节点，显然每个节点都会接到笛卡尔树上（中序遍历下的）最后一个位置，即笛卡尔树的右链末端。但我们仍需要使笛卡尔树满足关于 \(w\) 的性质，因此我们需要找到右链上第一个可以作为当前节点父亲的节点（例：如要维护小根堆，则找到第一个满足 \(w_p < a_i\) 的 \(p\)），并将该节点的右儿子变为新节点的左儿子。

下图（来自 OI-wiki）就展示了一棵笛卡尔树和其构建过程，其中红框部分为右链，绿色节点为新插入的节点。

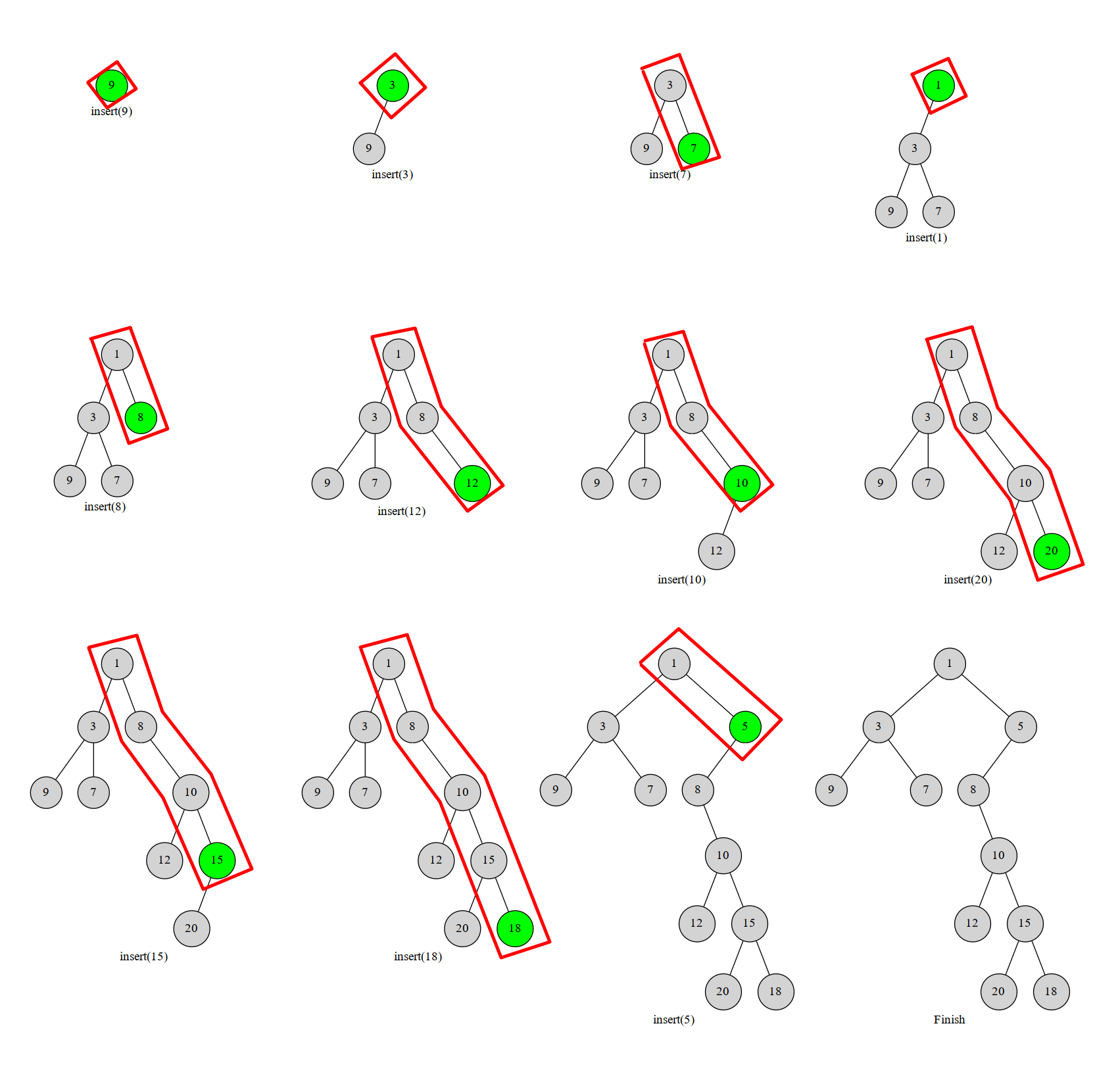
显然，对于每个右链上的节点，其只会被插入删除一次，而每次插入节点进行的其他操作的时间复杂度又是 \(O(1)\) 的，故构建笛卡尔树的时间复杂度为 \(O(n)\)。

这部分的代码：

void insert(int w) {
	a[++cnt].w = w;
	a[cnt].l = a[cnt].r = 0;
	
	int cur = top;
	while (cur && a[sta[cur]].w > w) --cur;
	if (cur) a[sta[cur]].r = cnt;
	if (cur < top) a[cnt].l = sta[cur + 1];
	top = cur;
	sta[++top] = cnt;
	if (top == 1) rt = cnt;
}

洛谷 P5854 【模板】笛卡尔树 的代码：

点击查看代码 
#include <bits/stdc++.h>
#define ll long long
#define int long long

using namespace std;

constexpr int N = 1e7 + 5;

struct Cartesian_Tree {
	int cnt, rt, top;
	int sta[N];
	struct Node {
		int l, r;
		int w;
	} a[N];
	
	void init() {
		cnt = rt = top = 0;
	}
	
	void insert(int w) {
		a[++cnt].w = w;
		a[cnt].l = a[cnt].r = 0;
		
		int cur = top;
		while (cur && a[sta[cur]].w > w) --cur;
		if (cur) a[sta[cur]].r = cnt;
		if (cur < top) a[cnt].l = sta[cur + 1];
		top = cur;
		sta[++top] = cnt;
		if (top == 1) rt = cnt;
	}
	
	int Solve1() {
		int res = 0;
		for (int i = 1; i <= cnt; ++i) {
			res ^= i * (a[i].l + 1);
		}
		return res;
	}
	
	int Solve2() {
		int res = 0;
		for (int i = 1; i <= cnt; ++i) {
			res ^= i * (a[i].r + 1);
		}
		return res;
	}
} CT;

int n;
int a[N];

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
		
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
	}
	
	CT.init();
	for (int i = 1; i <= n; ++i) {
		CT.insert(a[i]);
	}
	
	cout << CT.Solve1() << ' ' << CT.Solve2() << '\n';
	
	return 0;
}

笛卡尔树建排列的二叉查找树（BST）

定义对一个序列建立的 \(\text{BST}\)，为按顺序向一棵空 \(\text{BST}\) 中插入序列的项所得到的 \(\text{BST}\)。

笛卡尔树可以 \(O(n)\) 地对 排列 建 \(\text{BST}\)。

具体地，我们可以发现，对排列建立的 \(\text{BST}\)，其权值满足二叉查找树的性质；下标满足小根堆的性质。

于是对排列的每一项，设其权值为 \(k\)，下标为 \(w\) 并建立笛卡尔树，树的形态与对该排列建立的 \(\text{BST}\) 形态相同。

例：

  • P1377 [TJOI2011] 树的序

    容易发现得到 \(\text{BST}\) 后，其前序遍历就是字典序最小的生成序列。于是直接按照上述方式建笛卡尔树并按照前序遍历输出即可。

笛卡尔树维护直方图

注意，这里的直方图并不指一般意义上统计数据的模型，而是指一定数量的矩形在同一水平线上连续排列形成的图形。笛卡尔树可以方便地解决和直方图子矩形面积相关的问题。

例：

posted @ 2025-07-11 14:55  zyb_txdy  阅读(19)  评论(0)    收藏  举报