ω(n)，d(n) 与高合成数

定义 \(\omega(n)\) 表示正整数 \(n\) 的不同质因子个数。

一个显然的不等式是 \(\omega(n) \le \log n\)。但这是一个很松的上界，在 \(n \le 10^{18}\) 时上好像有 \(\max_{i = 1}^{n}\omega(i) \approx \log_{10} n\)。

有些时候我们需要枚举 \(1\) 到 \(n\) 中所有数的质因数，可以发现其时间复杂度与埃氏筛复杂度相同，为 \(O(n \log \log n)\)。

---

定义 \(d(n)\) 表示正整数 \(n\) 的不同约数个数。

关于它也有一个很松的不等式：\(d(n) \le \sqrt n\)。更紧的估计我们会在后面提到。

有些时候我们需要枚举 \(1\) 到 \(n\) 中所有数的约数，时间复杂度就是 \(O(\frac{n}{1} + \frac{n}{2} + \dots + \frac{n}{n}) = O(n \ln n)\)。

还有些时候我们的复杂度可能与 \(\max_{i = 1}^{n} d(i)\) 有关，但我们无法向 \(\omega(n)\) 一样，得出一个对 \(d(n)\) 的不错的估计。因此邪恶的出题人可能会故意去一个 \(d(n)\) 很大的 \(n\) 来卡我们，而这样的 \(n\) 有一个专业的名称：高合成数。

这里 是 vfk 的一篇关于高合成数的不错的文章，里面有一个关于 \(\max d(n)\) 的奇怪的估计。

这里 是高合成数的维基百科。

最后还是放一些表格和一些比较常用的估计吧。

\(n \le\)	\(\max \text{HCN}\)	\(\max{d(n)}\)
\(100\)	\(60\)	\(12\)
\(10^3\)	\(840\)	\(32\)
\(10^4\)	\(7560\)	\(64\)
\(10^5\)	\(83160\)	\(128\)
\(10^6\)	\(720720\)	\(240\)
\(10^8\)	\(73513440\)	\(768\)
\(10^9\)	\(735134400\)	\(1344\)
\(10^{18}\)	\(897612484786617600\)	\(103680\)

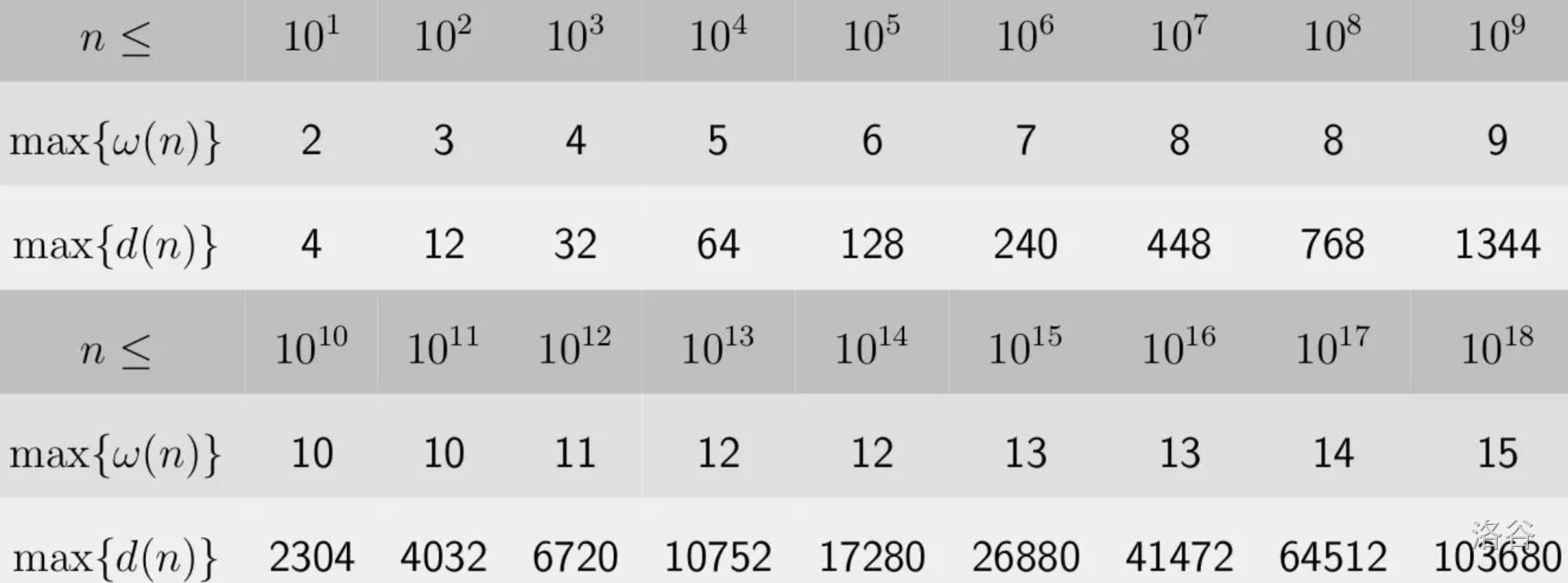
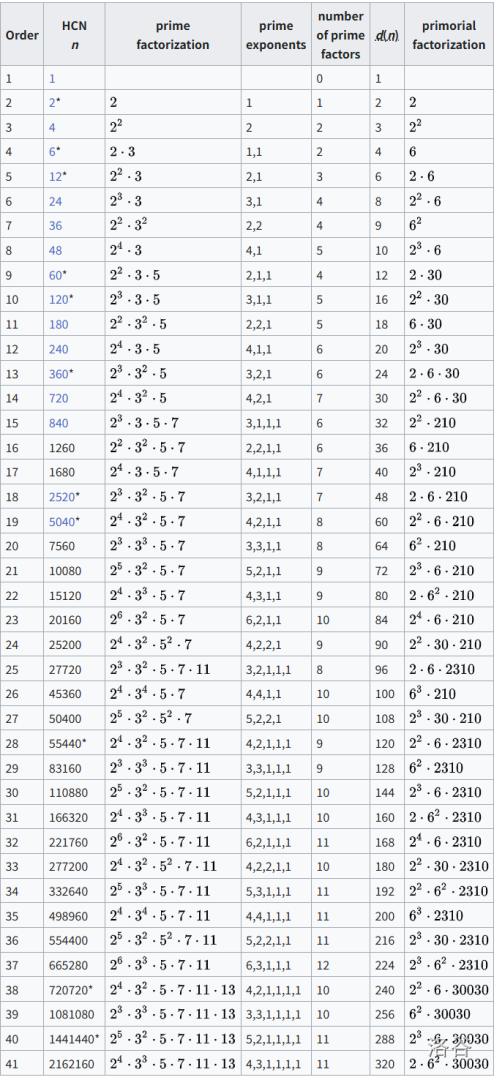
更全的高合成数表格（美中不足的是，这里没有相应的 \(d(n)\)）