别样的典题大战 2

CF1153D

考虑 dp。设 \(f_{u,0/1}\) 表示以 \(u\) 为根的子树让 \(u\ge ans\) 至少需要在子树内放几个 \(1\)（其中 \(0\) 为 \(<ans\)，\(1\) 为 \(\ge ans\)）。

转移使用调整法即可。

代码

CF1696D

不是哥们？我自己发明的东西不会了？

注意到全局最小值和全局最大值之间必然要跨一次。于是考虑分治，每次拆成 \(l\) 到一个极值，\(r\) 到另一个极值，用你喜欢的 RMQ 算法即可（事实上 ST 表效率最好）。

代码

CF2002E

观察样例，我们发现答案是单调不降的。经过进一步思考，我们发现，在后面加东西事实上并不会影响到前面的消消乐，所以我们其实只关心最后一段延长了多久。

于是维护一个单调栈，用最后一段尝试创掉栈里的不同颜色段，创不动了就停下；遇到相同颜色的就合并。合并之后的个数是最后一段的 \(a\) 加上栈内存储的这一段的 \(a\) 减去创掉的最长一段的异色的 \(a\)。

代码

CF618F

考虑强化限制，我们不选子集，而去选区间。

定义前缀和数组 \(sa,sb\)，不妨设 \(sa_n<sb_n\)。然后对于每一个 \(i\in[0,n]\)，找到最小的 \(sb_j\) 使得 \(sb_j\ge sa_i\)，显然两者的差在 \([0,n-1]\) 中，取值共 \(n\) 种。

那么我们有 \(n\) 种取值，\(n+1\) 对数，显然存在两对数差相等，然后这两对简单移项一下发现可以作为答案，于是选区间有解，进而选子集有解。直接双指针即可。

代码

CF464E

朴素做法是硬写高精度，但是显然过不去。

不难发现边权有一些特殊性质，所以我们可以考虑用数据结构维护二进制串。只需支持比较大小和加 \(2^x\) 即可。

于是使用主席树维护哈希，比较大小在主席树上二分 lcp 即可。单点加相当于一段区间置 \(0\) 再把一个点设成 \(1\)，二分最长 \(1\) 段即可，置 \(0\) 直接把这一段连向空树就行，单点修改显然好做。

然后再维护个堆搞一搞即可。

代码

LOJ2392

为什么我推出来所有性质了还是不会做？？？

先二分是显然的。

注意到，如果两个人提前相遇，而拿烟花的人还没有燃尽，那我等到燃尽的那一刻再传递是优的。

所以我们可以转化一下，你有一个电池，初始有 \(t\) 格电，一秒会掉一格电，遇到一个人就充 \(t\) 格电，然后速度要乘上 \(2\)，你需要保证任意时刻电量非负。

这个直接把 \(k\) 左右两边的部分拉出来一个 \((cost,val)\) 的序列对，然后相当于你在两个序列上按顺序取，如果当前还有至少 \(cost\) 格电，就可以加上 \(val\)。

然后你发现直接贪爆掉了，但是这个东西又不太能 dp。搞一搞发现，如果说你当前取了一段，但是贡献和是负的，那我拐回去显然劣完了，也就是说，我至少要拿到正贡献才会拐弯。所以你把两个序列对划分成若干个 \(val>0\) 的极短连续段，但是会剩下一个可空后缀无法划分。

然后对于这个后缀，考虑时光倒流，每次相当于先减去 \(val\)，再加上 \(cost\)。显然这个后缀经过时光倒流之后一定能被划分。

于是对这两部分分别进行检验即可。

代码

P1251

看到题可以想到把一天拆成上下午是更好做的。

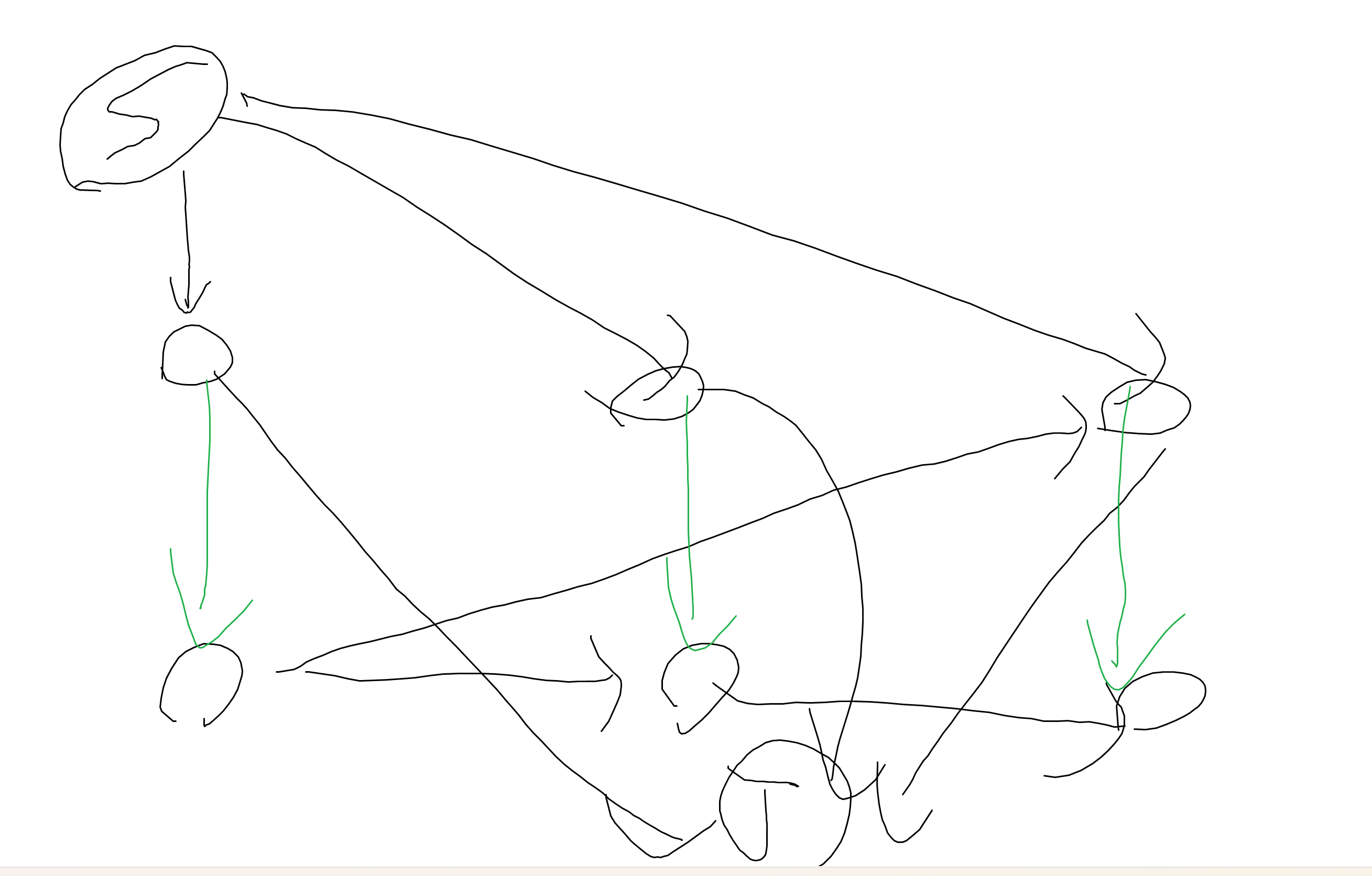
一开始的想法可能是这样的，但是你发现，如果在上午我获得了 \(r\) 个餐巾，我会直接跑到汇点，而不能传到后面的某一天。显然发现是绿色的边出了问题。考虑挪一下这些边，改到从源点流出。

因为你上午一定会用 \(r\) 条餐巾（多了不优，少了不合法），所以你下午会剩下 \(\le r\) 条用过的，剩下的被扔垃圾桶了，然后你只需要让这些餐巾分别往后拖延，或者送到某个店里即可。

代码

P3643

居然是超级典题。

首先你考虑设 \(f_{i,j}\) 表示前 \(i\) 个，第 \(i\) 个必须参赛且派了 \(j\) 个的方案数，转移枚举 \(p<i,k<j\) 即可。

这样做的复杂度是 \(O(n^2V^2)\)，可以获得足足 \(0\) 分。

你发现这个状态里带了个值域，而值域大的比较离谱，所以显然要把值域给去掉。那么去掉首选的方式显然是离散化。

离散化之后相当于说，你现在有 \(O(n)\) 个段，然后你要把 \(n\) 个队划分为若干段，使得每段里的队要么不参赛要么落在同一个值域段，且整体值域段单调上升。

不难发现改一下 dp 状态即可，设 \(f_{i,j}\) 表示前 \(i\) 个，第 \(i\) 个必须参赛且人数落在第 \(j\) 个值域段的方案数，转移仍然枚举 \(p<i,k<j\) 即可。此时我们默认 \([p+1,i]\) 的人数要么为 \(0\)，要么在第 \(j\) 个段内，且非 \(0\) 部分需要单调上升，同时 \(i\) 不能是 \(0\)。你发现这个看起来一大坨的东西不太好算？

不妨设有 \(m\) 个位置可以放非 \(0\) 数，同时第 \(j\) 个值域段长度为 \(len\)。我们先枚举 \(i\) 到底用了哪个数，则剩下的部分都要小于 \(i\) 用的数。于是剩下有 \(m-1\) 个位置，还有 \(len-i\) 个数可以用。只需先选 \(j\) 个位置放非 \(0\)，再选 \(j\) 个数扔给它们。式子如下：

\[\displaystyle\sum_{i=1}^{len}\sum_{j=0}^{m-1}\binom{m-1}{j}\binom{len-i}{j} \]

变形一下上个范德蒙德卷积就变为了：

\[\displaystyle\sum_{i=1}^{len}\binom{m+len-i-1}{m-1} \]

不难发现这个式子其实就是 \(\binom{m+len-1}{m}\)。

于是我们的转移就是 \(\displaystyle f_{i,j}=\sum_{p<i,k<j}f_{p,k}\binom{m+len-1}{m}\)。

因为 \(len\) 太大了，所以我们需要动态维护组合数，只需倒着扫 \(p\) 并考虑是否乘上 \(\dfrac{m+len}{m+1}\) 即可（动态维护 \(m\)），注意初始 \(m=1\)。

直接做的时间复杂度是 \(O(n^4)\)，对 \(\displaystyle\sum_{k<j}f_{p,k}\) 做前缀和进行优化即可使时间复杂度降为 \(O(n^3)\)，可以通过。

代码

CF1845E

这种神秘 01 串交换问题和选两个相邻相同位置取反是等价的。我们一般把其归约到交换上，因为交换具有一些更好的性质。

例如说，\(1\) 的数量是恒定不变的，且你可以通过两个序列中 \(1\) 的位置算出用了多少次交换操作。这显然是简单的。

于是我们有一个显然的状态 \(f_{i,j,x}\) 表示前 \(i\) 个位置，放了 \(j\) 个 \(1\)，此时最少用了 \(x\) 次操作的方案数。转移显然是 \(O(1)\) 的，于是你做到了 \(O(n^2k)\)。

然后你就发现，这个 dp，优化不了一点！

所以考虑拆贡献，用点算贡献太慢了，那就用边算，我们只需要知道每条边被经过了多少次即可。

于是设 \(f_{i,j,x}\) 表示前 \(i\) 个位置，前 \(i\) 个位置中 \(1\) 的个数比初始状态前 \(i\) 个位置中 \(1\) 的个数多了 \(j\) 个，此时最少用了 \(x\) 次操作的方案数（\(j\) 可以是负数）。不难发现，此时 \((i,i+1)\) 这条边会被经过 \(\operatorname{abs}(j)\) 次。

但是，这个东西不还是 \(O(n^3)\) 同阶的吗。注意到如果说你这一段里多了 \(t\) 个，那你显然要把这些挪到段外面，而这 \(t\) 个距离段右端点的距离必然各不相同，所以你挪的总步数是 \(O(t^2)\) 的。也就是说，\(j\) 事实上只有 \(O(\sqrt k)\) 量级。

转移仍然 \(O(1)\)，最终复杂度是 \(O(nk\sqrt k)\) 的。

代码

P3561

在说这道题之前，我们先说一下竞赛图最小字典序哈密顿路径 \(O(n^3)\) 怎么做。

首先需要知道，强连通竞赛图有哈密顿回路。

做法 \(1\)：因为竞赛图有哈密顿路径，所以每次我走最小的点，然后把上一个点删掉，剩下的图还是竞赛图，所以仍然有哈密顿路径。所以直接贪心即可。

这样做显然错误。这是因为，竞赛图不一定从任何点出发都有哈密顿路径。

做法 \(2\)：先缩 scc，然后 scc 内采用上一个做法的贪心，scc 间直接走最小的点。

感觉有点道理。但是实际上 scc 删掉一个点就不一定是 scc 了，所以这个图仍然是普通竞赛图，所以此做法仍然是假的。

显然我们不妨设整张图是一个 scc，因为 scc 间之间走最小的肯定没问题。

首先我先取最小的点作为出发点，目前仍然是有哈密顿路径的，这个显然没问题，

现在问题是，去掉这个点之后，图不一定是 scc 了，所以贪心就错了。

那就有一个想法，我把这个点删掉之后，再对剩下那一坨重新缩 scc，然后走到第一个 scc 里最小的点。这样走是显然正确的。

如果你采用 tarjan 缩 scc，那么这样做的时间复杂度就是 \(O(n(n+m))\)，近似可以看做 \(O(n^3)\)。

然后考虑这个题怎么做，你发现这个题唯一的区别就是，把求最小解变成了求可行解。

首先缩 scc。

先考虑怎么求一个哈密顿路径。只需增量构造，到 \(i\) 的时候，把 \(i\) 插入到一个能插入到的空隙中即可。不难证明，\(i\) 一定可以插入到原来的链中。

然后考虑怎么在这个的基础上构造哈密顿回路。就维护一个 \(s,t\)，使得 \(t\) 能直接到 \(s\)。然后每次遇到一个能直接到环上的点，就把这个点以及前面的一坨全插到环里并更新 \(s,t\)，具体细节见代码。

这样是可以直接把所有点作为出发点的答案求出来的。同时，因为我们每次遍历的是点而不是边，所以这样做的时间复杂度是 \(O(n^2)\)。

好吧好像没过这题看不到代码，那直接看题解实现吧，写的还是挺清楚的。

代码