ρars/ey 题解

给个链接：ρars/ey。

我们考虑一个树上背包。

设 \(f_{u,i}\) 表示在 \(u\) 号节点的子树内删除 \(i\) 个点的最小代价。显然有答案为 \(f_{1,siz_1-1}\)。

接下来我们考虑转移。看这一张图：

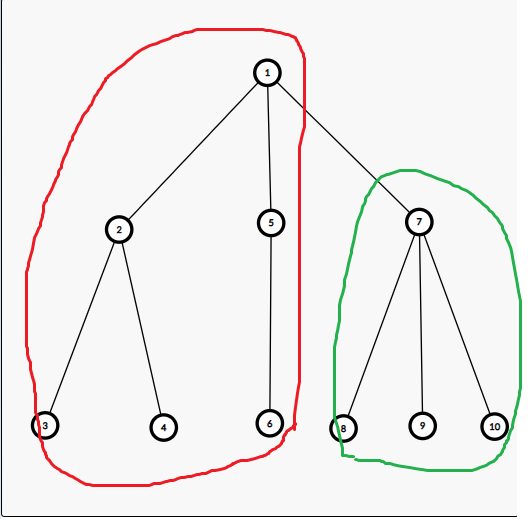
这里红圈内的东西为当前的 \(siz_u\)，绿圈部分为 \(siz_j\)。

我们枚举 \(x\) 为 \(u\) 子树内已经被删掉的点的数量。考虑 \(x\) 的上界为红圈加绿圈减去 \(u\) 和 \(u\) 的儿子。

所以是 \(siz_u+siz_j-cnt-1\)，其中 \(cnt\) 为当前是 \(u\) 的第几个儿子。

然后再枚举一个 \(y\)，代表 \(j\) 子树内删掉点的数量。

于是我们有 \(f_{u,x}=\min(f_{u,x},f_{u,x-y}+f_{j,y})\)。

接着就是在跑完所有儿子后，再把剩下的点处理掉。具体就是枚举一个 \(i\)，然后 \(f_{u,siz_u-1}=\min(f_{u,siz_u-1},f_{u,i}+a_{siz_u-i-1})\)，其中 \(i\) 为代价。

代码：

#include<bits/stdc++.h>
#define int long long
#define N 5005
#define M 10005
using namespace std;
int n,a[N],siz[N],f[N][N];
int h[N],e[M],ne[M],idx;
//f_{u,i}表示u节点子树删了i个的代价 
void add(int a,int b){
	e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}
void dfs(int u,int fa){
	siz[u]=1;
	int cnt=0;
	for(int i=h[u];~i;i=ne[i]){
		int j=e[i];
		if(j==fa)continue;
		dfs(j,u);
		cnt++;
		for(int x=siz[u]+siz[j]-cnt-1;x;x--){
			for(int y=max(x-siz[u],1ll);y<=x&&y<siz[j];y++){
				f[u][x]=min(f[u][x],f[u][x-y]+f[j][y]);
			}
		}
		siz[u]+=siz[j];
	}
	for(int i=0;i<=siz[u]-cnt-1;i++){
		f[u][siz[u]-1]=min(f[u][siz[u]-1],f[u][i]+a[siz[u]-i-1]);
	}
}
signed main(){
	cin>>n;
	for(int i=1;i<n;i++){
		cin>>a[i];
	}
	memset(h,-1,sizeof h);
	for(int i=1;i<n;i++){
		int a,b;
		cin>>a>>b;
		add(a,b);add(b,a);
	}
	memset(f,0x3f,sizeof f);
	for(int i=1;i<=n;i++){
		f[i][0]=0;
	}
	dfs(1,0);
	cout<<f[1][siz[1]-1];
	return 0;
}