离散数学2 集合论

离散数学2 集合论

---

目录

• 离散数学2 集合论
• 第6章 集合代数
  • 集合的基本概念
  • 集合的运算
  • 集合恒等式
• 第7章 二元关系
  • 有序对与笛卡尔积
  • 二元关系
    • 特殊关系
  • 关系的表示
  • 关系的运算
    • 基本运算
    • 关系的幂运算
  • 关系的性质
    • 关系上的性质的判别
  • 关系的闭包
    • 关系闭包的计算公式
  • 等价关系
    • 等价类的性质
    • 商集与划分
  • 偏序关系
    • 偏序集中的元素的可比与覆盖
    • 偏序集中的特殊元素
    • 偏序集的特殊子集
• 第8章 函数
  • 函数的定义与性质
    • 函数
    • 函数相等
    • 特殊函数
    • 函数的像与完全原像
    • 函数的性质
  • 函数的复合和反函数

---

第6章 集合代数

集合的基本概念

• 集合：把一些事物汇集到一起组成一个整体就称为集合

• 元素：这些食物就是集合的元素或成员

• 集合的表示：列举法，概括属性法，文氏图

• 元素与集合的关系

  • 属于
  • 不属于

• 同一层级上的两个集合之间的关系

  • 包含，子集
    

  • 相等
    

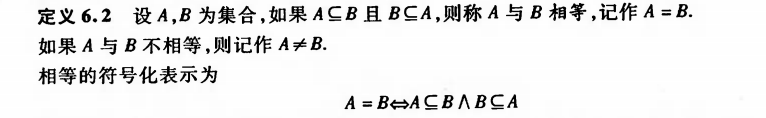
  • 真子集
    

  • 空集
    

  • n元集
    

  • 幂集
    ：

  • 全集
    

集合的运算

• 交集
  

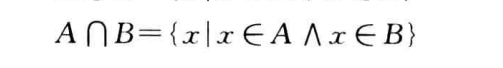
• 并集
  

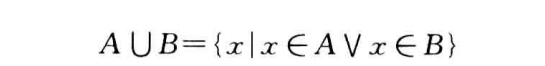
• 相对补集
  

• 对称差集
  

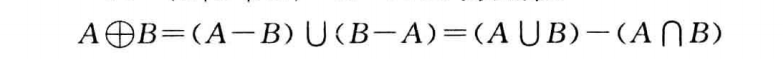
• 绝对补集
  

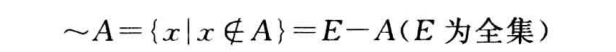
• 广义并
  

• 广义交
  

  运算的优先顺序

  

集合恒等式

第7章 二元关系

有序对与笛卡尔积

有序对

笛卡尔积

二元关系

特殊关系

• 空关系 恒等关系 小于等于关系 整除关系 包含关系

关系的表示

关系的运算

基本运算

关系的幂运算

关系的性质

关系上的性质的判别

关系的闭包

关系闭包的计算公式

等价关系

等价类的性质

商集与划分

偏序关系

偏序集中的元素的可比与覆盖

偏序集中的特殊元素

偏序集的特殊子集

第8章 函数

函数的定义与性质

函数

函数相等

特殊函数

函数的像与完全原像

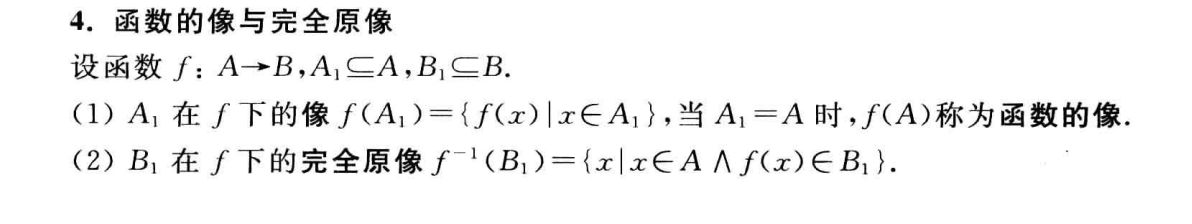
函数的性质

函数的复合和反函数