elliptic curves in the affine plane
我们讨论在仿射平面上的椭圆函数。


需要注意的点是:定义curve的多项式不仅需要在该域上是无重根的,还需要在任何代数闭包上是无重根的,在特征是p的非perfect的域上有反例。
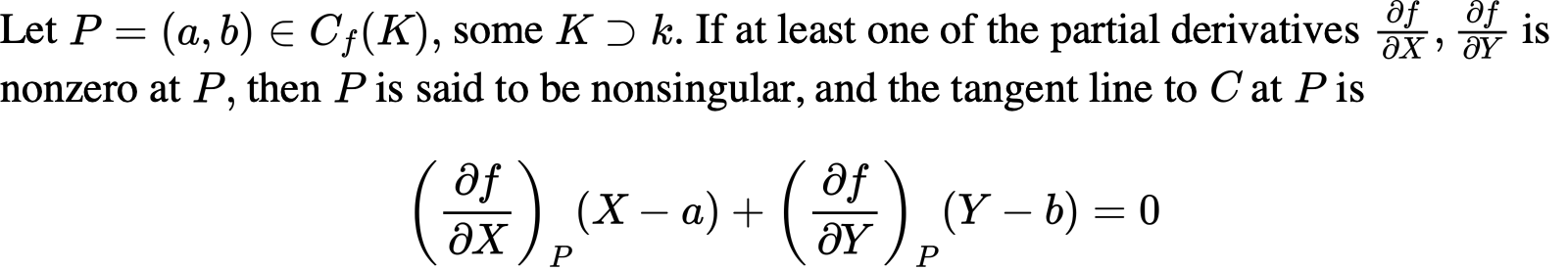
给定curve上的一个点,一个重要的技巧是,我们可以把原来的多项式改写为:

那如果取的点是singular的呢?



射影仿射面:
熟知的关系:



我们利用这个覆盖定义射影曲线的重数,切线......

Rational Points on Plane Curves

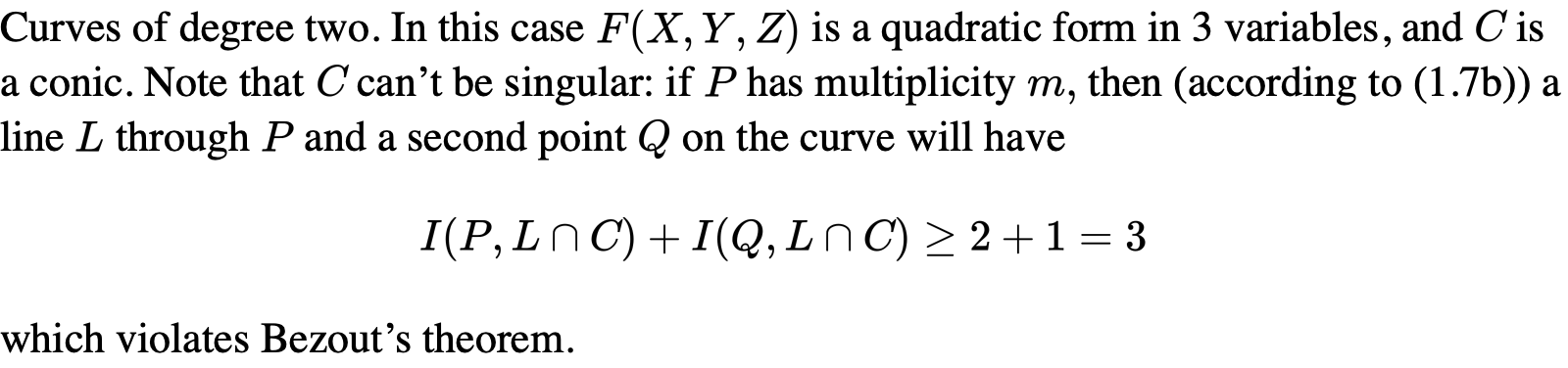
我们把R视作是P=\inf的情况,于是我们把一个Q上的多项式在Q里的根的问题转化到局部域上去:
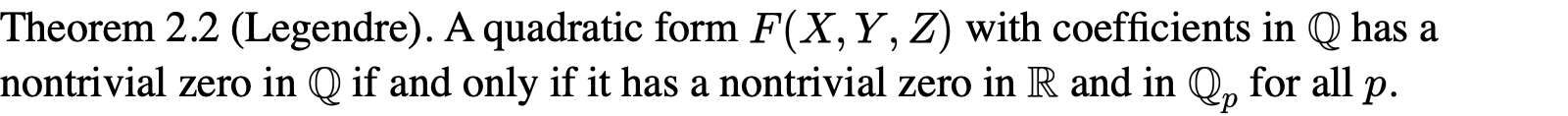
我们可以把定理加强到任意的变量和任意域上去(by Hasse-Minkowski theorem)

二次curves上的有理点实际上非常好被确定:




genus>1的curves:
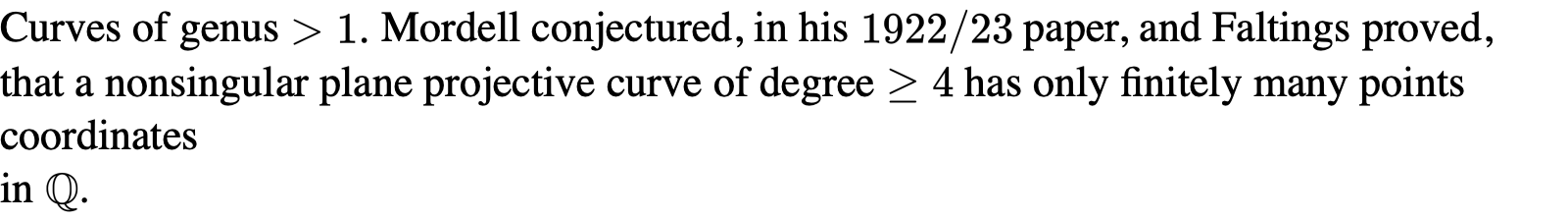
首先是定义射影平面曲线的几何亏格:
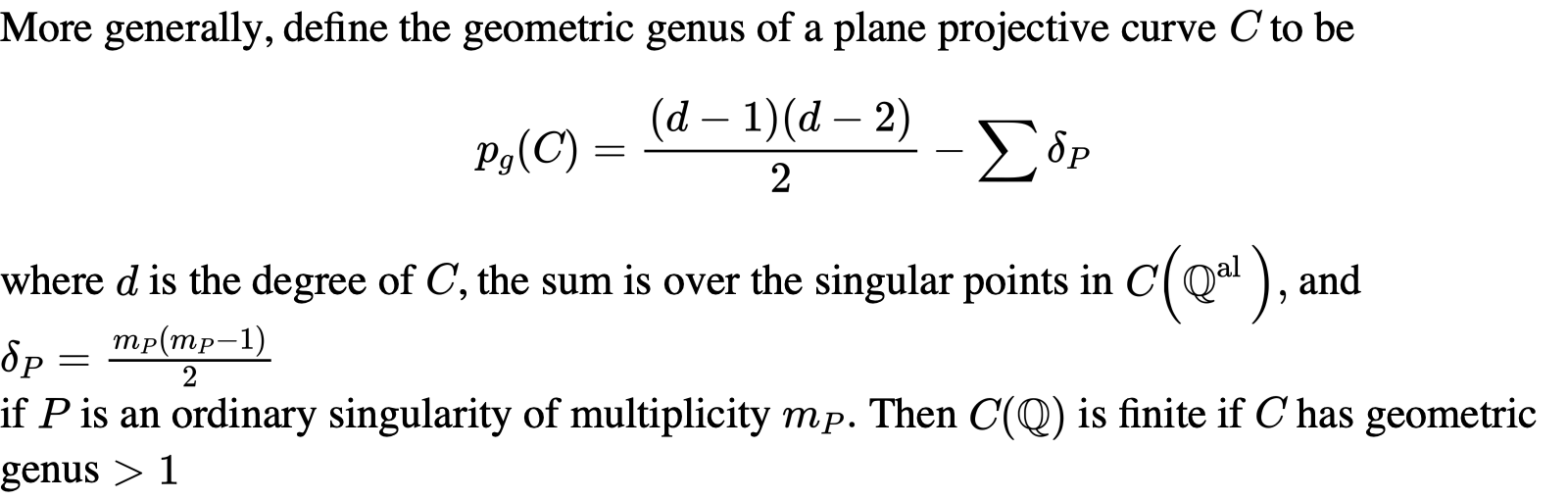

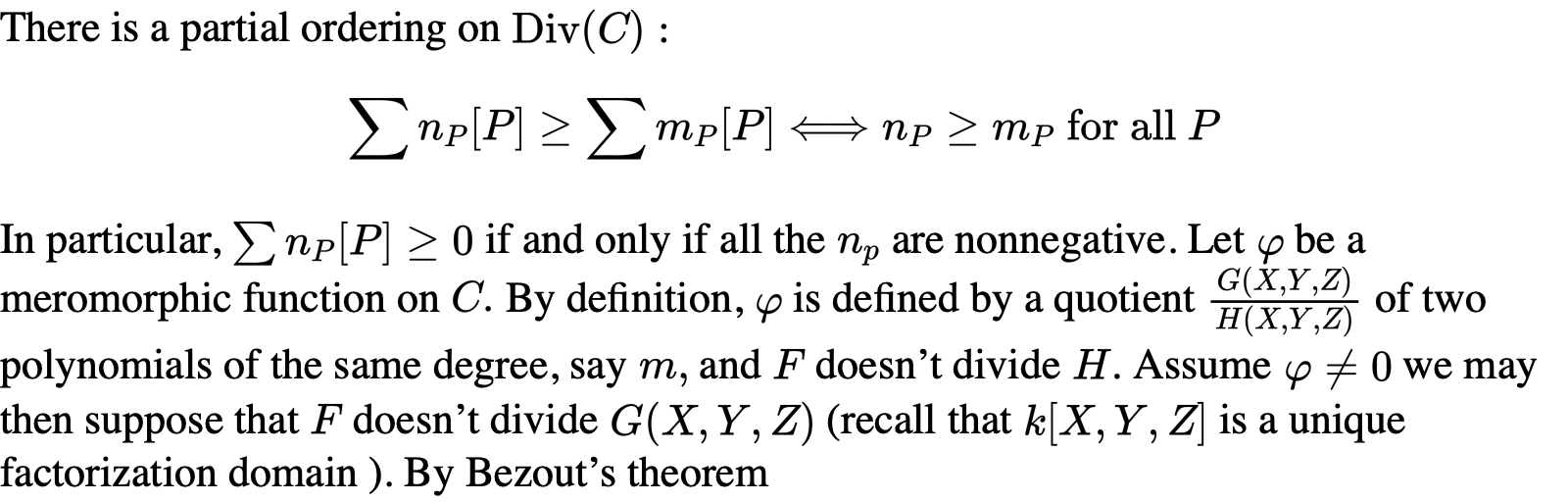






于是乎我们用Riemann-Roch定理证明了C(k)有一个群的结构:
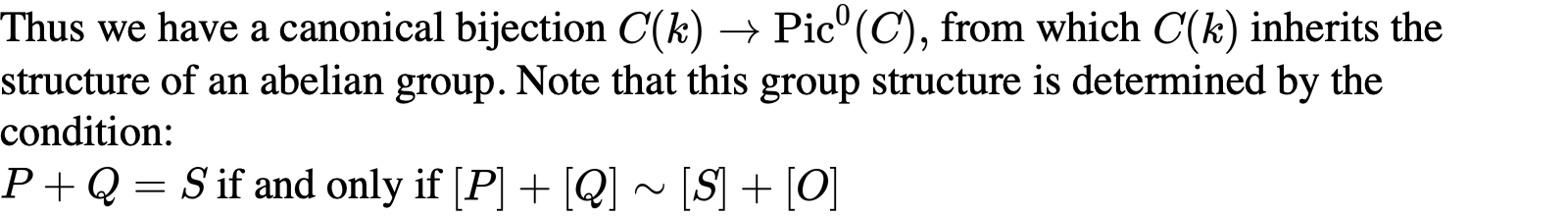





 浙公网安备 33010602011771号
浙公网安备 33010602011771号