【笔记】KMP

网上说法都不太一样，不管了，那我自己写。
简述：失配函数就是模板串构建的状态机，失配边的含义就是匹配失败后与文本串最大（从而具备序关系）重合情况的新的匹配位置。状态，指文本串各点在“匹配规则”的过程中在状态机上的“状态”。此外注意失配函数的性质。

模板题：给定文本串 \(T\) ，模板串 \(P\) ，查询 \(P\) 在 \(T\) 中所有出现位置（下标从 0 开始）。
先考虑 \(O(N^2)\) 朴素做法：

for (int i=0; i< N-M; i++) {
	int ok = 1;
	for (int j=0; ok && j< M; j++) if (P[j] != T[i+j]) ok = 0;
        // 注意到匹配失败就退出，意味着当前 j 以前都是匹配成功的。下文默认这种想法。
	if (ok) printf("%d ", i);
}

注意到 \(T\) 上的指针反复横跳，如果我们在失配时，并不是让这个指针跳回去，而是让 \(P\) 右移一些，再次使 \(T\) 的该指针以前的部分匹配上，我们就能继续了。而这个 \(P\) 至少要右移多少，我们希望能 \(O(1)\) 得知。
观察：假设当前匹配到了 P[j] != T[i+j] ，记 \(k=i+j\) ，那么 \(P[0...j-1]\) 和 \(T[i...k-1]\) 是相等的，如果重新从 \(T[i+1]\) 和 \(P[0]\) 开始匹配，要能顺利匹配完 \(T[k]\) 之前部分，说明 \(P[0...j-2]\) 和 \(P[1...j-1]\) 是相等的；同理，如果重新从 \(T[i+2]\) 和 \(P[0]\) 开始匹配，要能顺利匹配完 \(T[k]\) 之前部分，说明 \(P[0...j-3]\) 和 \(P[2...j-1]\) 是相等的...
即，在原始做法中，从上一次在 \(T[k]\) 失配开始，到下一次匹配到 \(T[k]\) (不管在该位是否匹配成功)，对于 \(P[0...j-1]\) 来说，满足其对应前缀（严格前缀）等于其后缀。
而我们只要知道对于当前已经匹配好的 \(P[0...j-1]\) ，下一次至少要从哪个位置开始比，那么就能保证 \(T\) 上的指针始终右移，就能做到 \(O(N)\) 了。显然，这个位移量就是最长的“那个前缀”长。
我们记失配（fair）指针 \(f[j]\) 表示对于 \(j\) ，下次 \(P\) 至少需要的位移。

void find() {
        getfail();
	int j = 0;
	for (int i=0; i< N; i++) {
		while (j && P[j]!=T[i]) j = f[j];
		if (P[j]==T[i]) j++;
		if (j==M) printf("%d\n", i-M+1);
	}
}

约定：若 \(P[0...j-1]\) 的一个严格前/后缀等于与其等长的后/前缀，称之为“公共前/后缀”；记 \(P[0...j-1]\) 最长公共前缀的长度为 border 。我们也已经知道了，\(f[j]\) 就是 border 。
我们注意到，对公共前缀再取一次公共前缀，和公共后缀的公共后缀是对应匹配的，所以递推：
首先，\(f[0] = 0\) ; \(f[1] = 0\) （因为 \(P[0...0]\) 没有严格前缀）
而对于 \(f[j] = x\)，表示最大的 \(x\) 满足 \(P[0...x-1] = P[j-x...j-1]\) ，等价于 \(P[0...x-2] = P[j-x...j-2]\) 且 \(P[x-1] = P[j-1]\) ，而前者是 \(P[0...j-2]\) 的一个公共前/后缀，也就是说，在 \(P[0...j-2]\) 的所有公共前/后缀中找一个满足 \(P[x-1] = P[j-1]\) 的最长的。
据说是“自己匹配自己”，但感觉就是个递推...随便吧...
画个图：

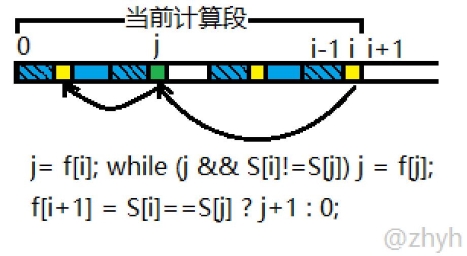
void getfail() {
	f[0] = 0, f[1] = 0;
	for (int i=1; i< M; i++) {
		int j = f[i];
		while (j && P[i]!=P[j]) j = f[j];
		f[i+1] = P[i]==P[j] ? j+1 : 0;
	}
}

模板：

#include <cstdio>
#include <cstring>
using namespace std;
const int MAXN = 1000005;
struct KMP {
	int N, M, f[MAXN]; char T[MAXN], P[MAXN];
	void init() {
		scanf("%s%s", T, P);
		N = strlen(T), M = strlen(P);
	}
	void getfail() {
		f[0] = 0, f[1] = 0;
		for (int i=1; i< M; i++) {
			int j = f[i];
			while (j && P[i]!=P[j]) j = f[j];
			f[i+1] = P[i]==P[j] ? j+1 : 0;
		}
	}
	void find() {
		getfail();
		int j = 0;
		for (int i=0; i< N; i++) {
			while (j && P[j]!=T[i]) j = f[j];
			if (P[j]==T[i]) j++;
			if (j==M) printf("%d\n", i-M+1);
		}
	}
} kmp;
int main()
{
	kmp.init();
	kmp.find();
	for (int i=1; i<=kmp.M; i++) printf("%d ", kmp.f[i]);
}

[BOI2009]Radio Transmission

题意简述：给你一个字符串 s1 ，它是由某个字符串 s2 不断自我连接形成的。但是字符串 s2 是不确定的，现在只想知道它的最短长度是多少。

关于公共前/后缀和循环节的关系题解

[POI2006]OKR-Periods of Words

题意简述：求“最小公共前/后缀”

由 fail 函数的性质，有类似“路径压缩”的做法：

for (int i=1; i<=N; i++) {
	int j = f[i];
	while (f[j]) j = f[j];
	f[i] = j;
}

[USACO15FEB]Censoring S

题意简述：一个字符串 S ，删除其中的子串 T （注意到删除之后，两端的字符串有可能会拼接出来一个新的子串 T ），不断重复这一过程，直到 S 中不存在子串 T ，输出 T

对于匹配过程中，文本串的每个位置，在状态机上的“状态”的理解。
P.S. 用栈处理太正解了...白瞎了线段树...

for (int i=0; i< N; i++) {
	while (j && T[j]!=S[i]) j = f[j];
	if (T[j]==S[i]) j++;
	stt[i] = j; // state_i
	if (j==M) { j = stt[findLastPosition(i)]; ... }
}

刷新页面返回顶部

zhyh's blog

【笔记】KMP

模板：

[BOI2009]Radio Transmission

[POI2006]OKR-Periods of Words

[USACO15FEB]Censoring S

[NOI2014] 动物园

[POI2005]SZA-Template

【模板】失配树

[HNOI2008]GT考试

公告