复习
导数概念题总结⭐⭐⭐
第七套 2T(导数极限概念总结)_哔哩哔哩_bilibili
前置知识
什么是可导
可导就是左右导数相等
振荡函数依然有可导的权利

导函数性质

结论是: \(f'_{-}(0)\)和\(\lim\limits _{x→0}f'(x)\) 这样的单侧导数和导数极限没有任何关系,两者任何以访存在都无法推导出另外一方存在
f(x) = x (x != 0)
lim f'(x) 由原函数求导得到
某点导数值由定义求
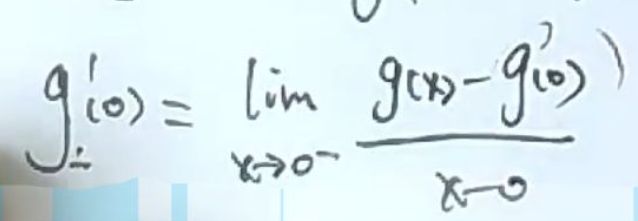
左右导都存在才能说明该点导数存在,而左右导存在且相等才能说明该点可导
本题是对于(0,+inf) 可导,对于 0 这一点是不一定可导的,因为右导数都不一定存在,因此左右导数不一定相等,因此
对这条就失效了,这条需要 左右导数存在且相等

一点推不了区间

⭐


导函数对原函数的几何角度
注意:趋于无穷的特殊情况⭐⭐⭐
近似水平线、或者振荡


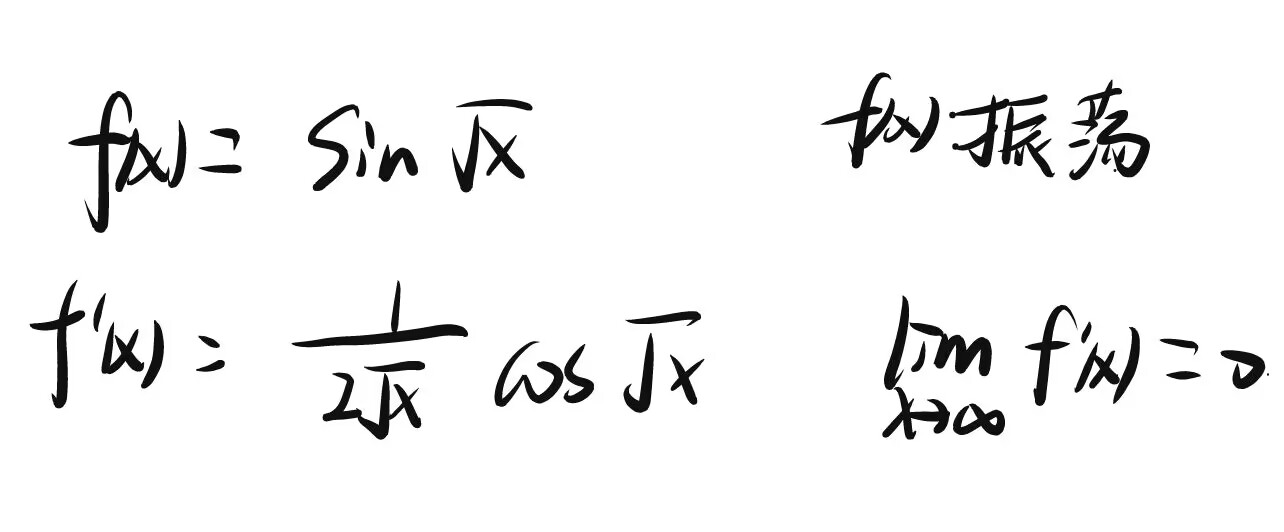
原函数推导函数(什么都推不出来)
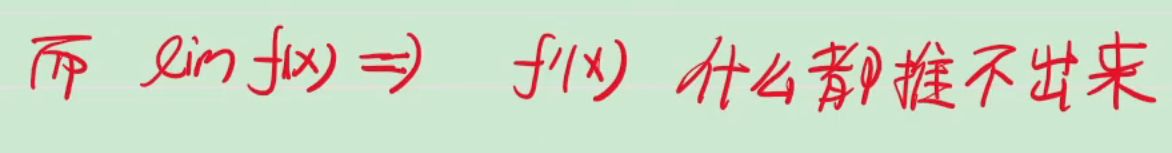
原函数为无穷,导函数极限各种情况都存在⭐⭐⭐
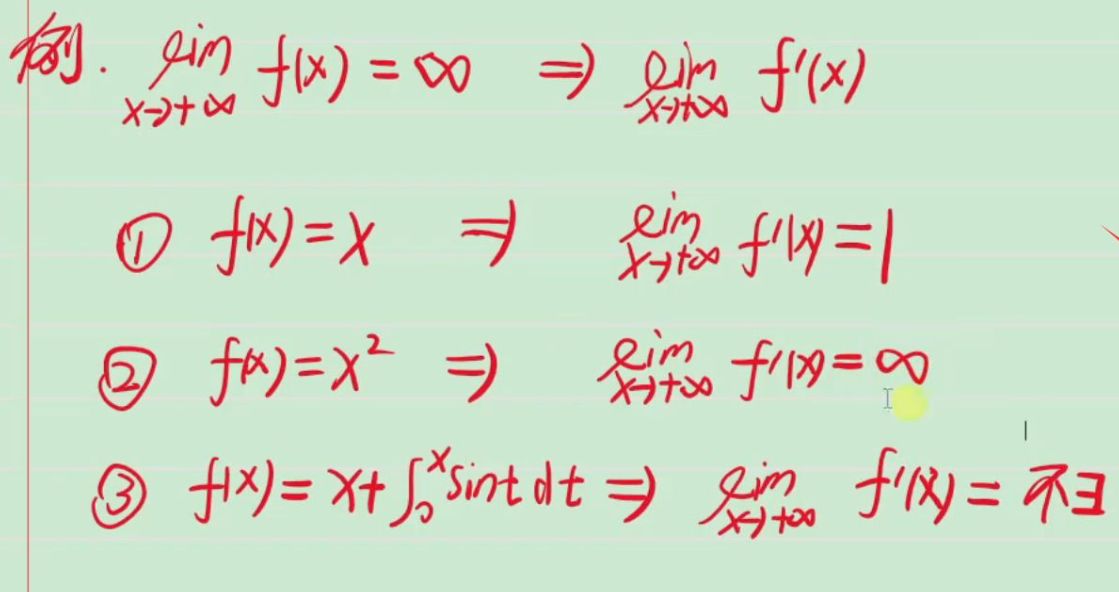
原函数存在,导函数极限可能为0,可能不存在⭐
^c383e7
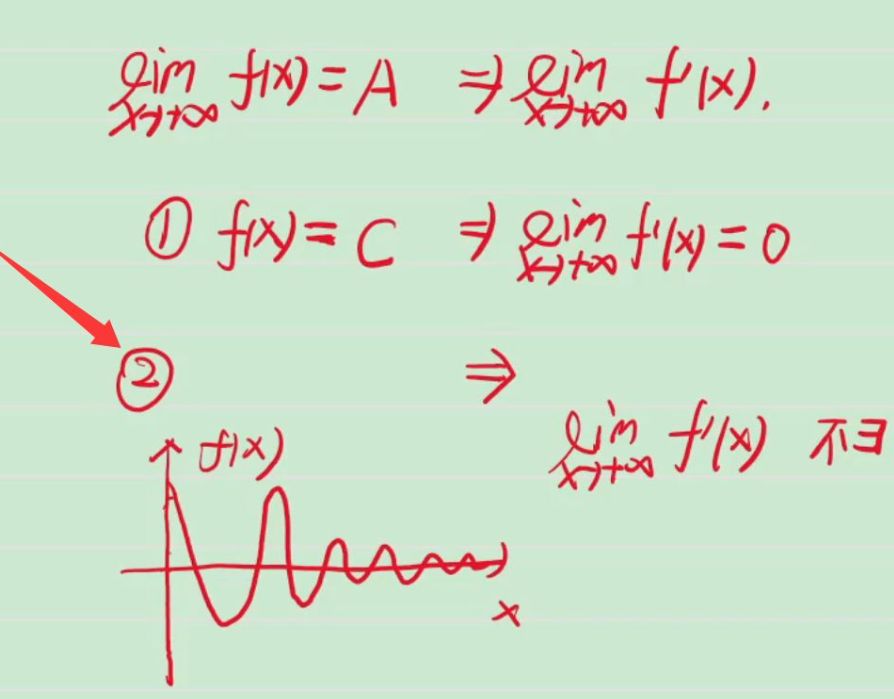
例题
C
原函数推导函数什么都推不出来,排除AD

B选项特例

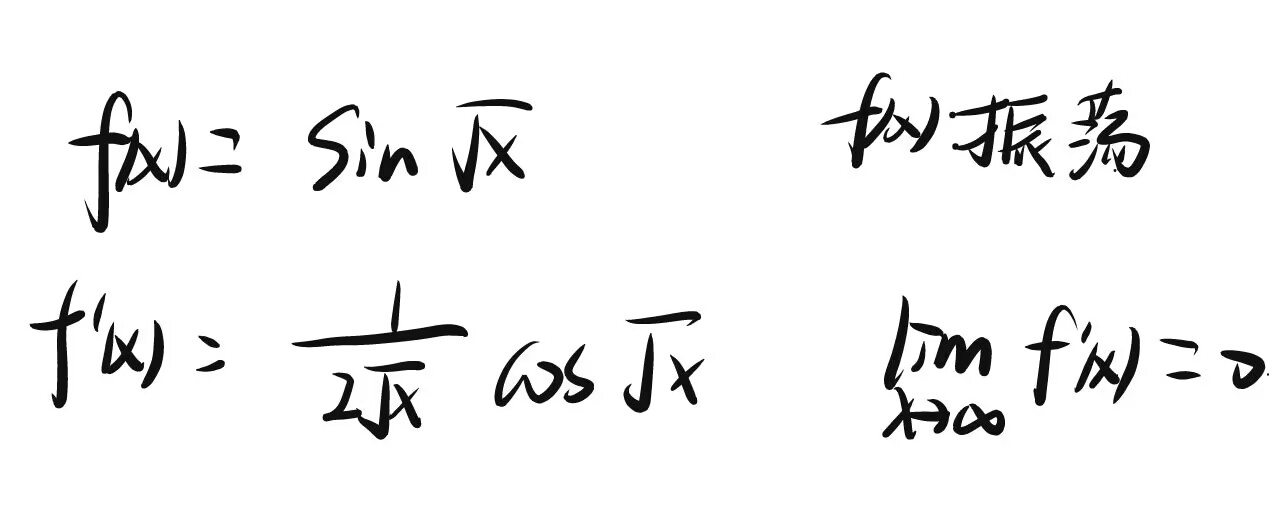
C选项若二阶导=A!=0,f(x)必定无界,冲突了,因此二阶导为0
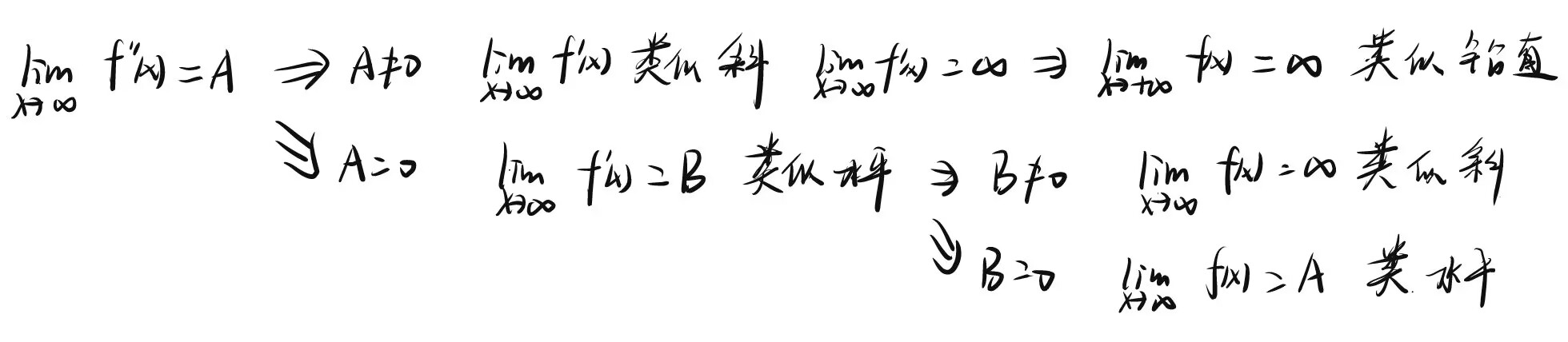
×⭐⭐⭐
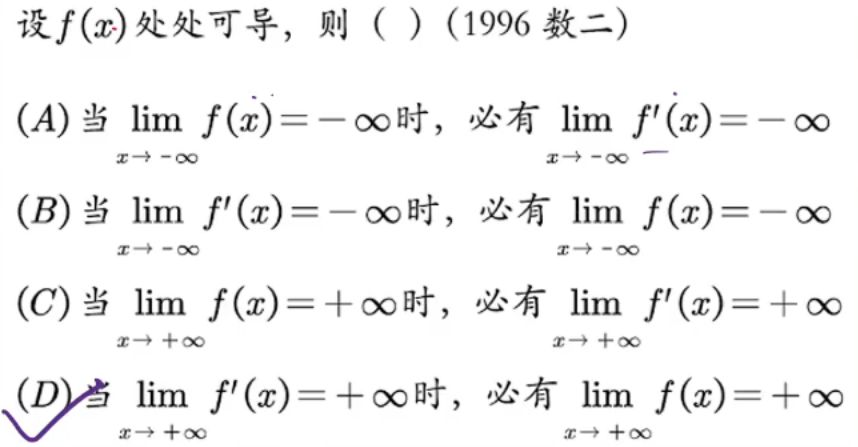
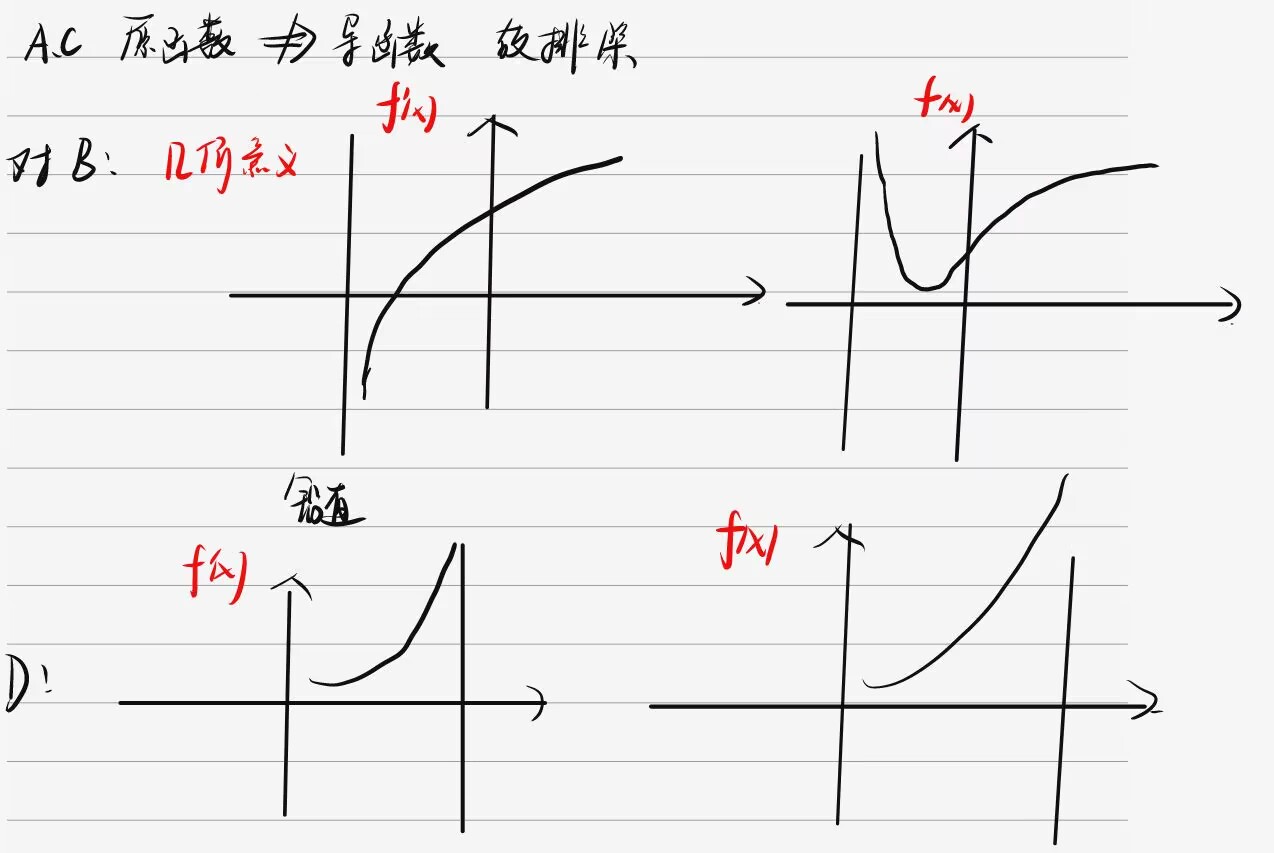

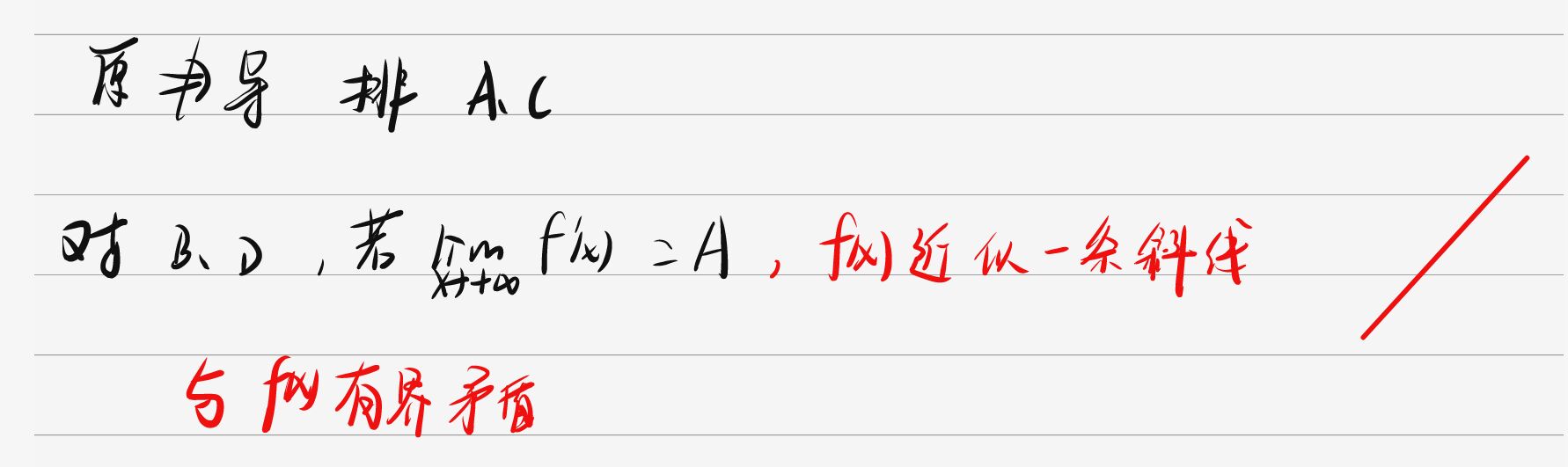
⭐⭐⭐



AB都是一点性质推区间,错误
C利用下面这条性质1
D选项可以为振荡,振荡处处可导,但是导函数不连续

可导就是左右导数相等


A选项:一点推不出领域
选C
???????????????

A是因为fx在x=a处可能不连续,如果fx连续,A就是对的
AB = BA 总结⭐⭐⭐


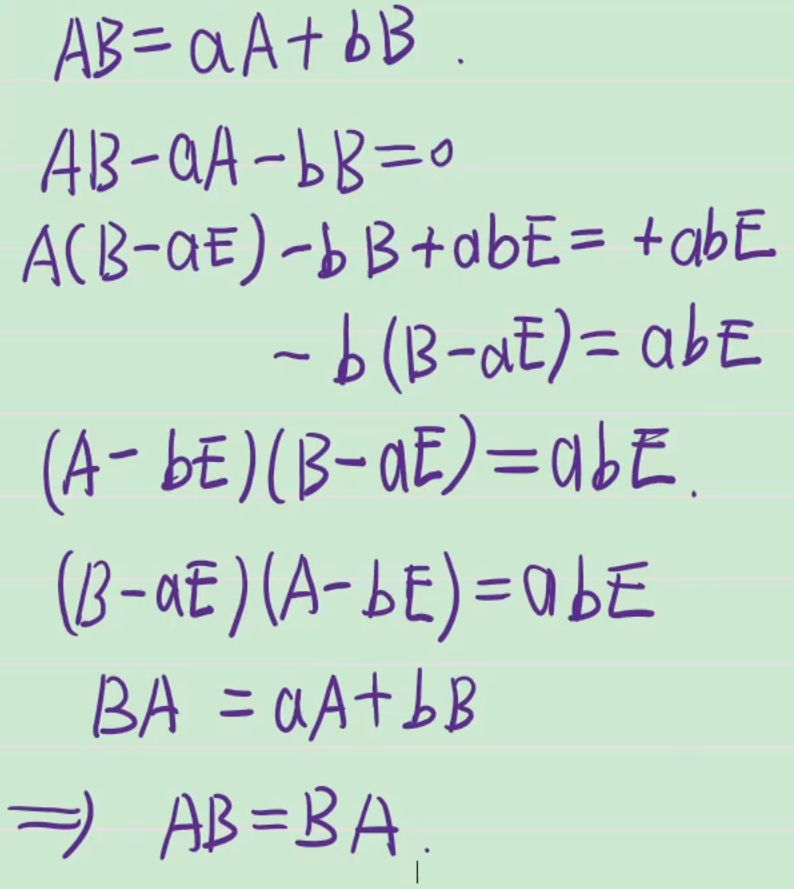
AB = BA 可以推出来什么
翻译:矩阵A是一个对角矩阵,并且它的对角线元素互不相同,而还存在一个矩阵B,如果A与B可交换,即AB=BA,那么B也是对角矩阵

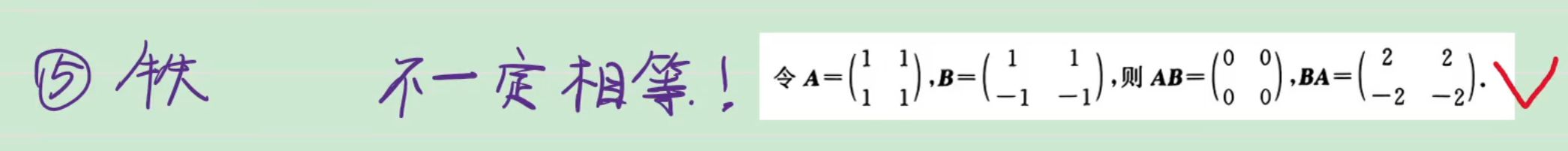
 ^44fa18
^44fa18
\(AA^T\)⭐⭐⭐
^bedd7e
用二次型的角度来看,就是一个平方和形式的二次型


反对称矩阵 \(A^T=A\)
主对角线上全为0,对称元素为相反数






真题证明题汇总⭐⭐⭐
777 混分
个人总结
基本手法
- 拉格朗日
- 柯西
- 考虑藏零点
- 尤其是出现 ln
- 构造原函数罗尔
- 泰勒(二阶导数以上)
- 积分不等式
- 通法:让一个常量变成变量求导观察单调性
- 双中值
- 不要求中值不等
- 分别采用柯西或者拉格朗日
- 要求不等
- 找一个分界点,对两个区间拉格朗日
- 不要求中值不等
讨论
证明 口口=0

f'' = 0
可以把一些东西看成导数形式
例如李六这题,f(x)看作一个变限积分的导数

泰勒

找原函数
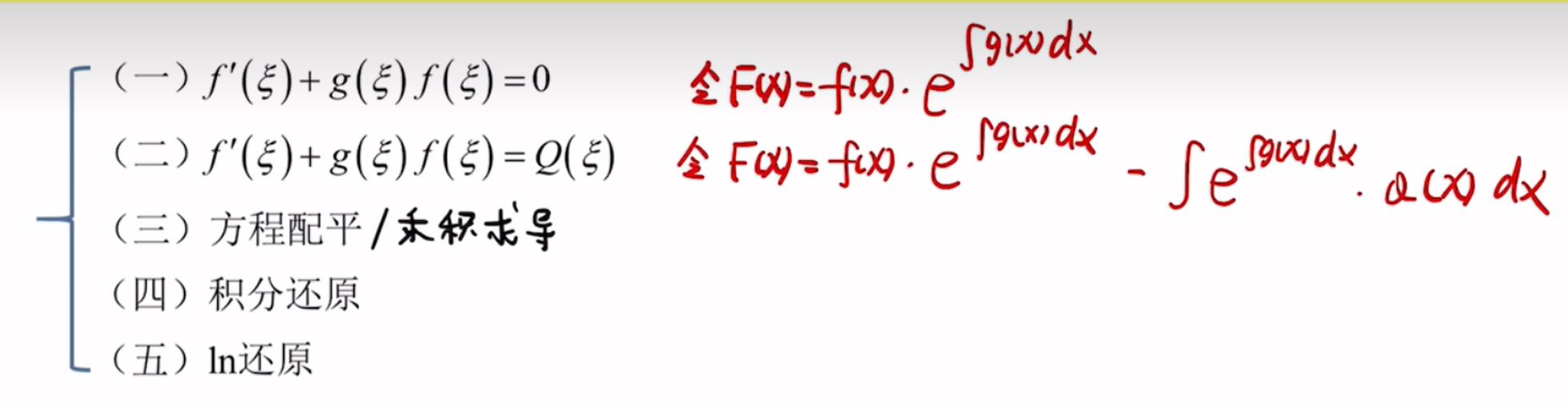
3(\(f^2\) 视作 \(f*f\) 然后微分方程,不定积分 转化为 [a,x] 的变限积分)⭐
4(\(f(x) - x\) 视作整体,\(f'(x) - 1\) 视作这个整体的导数)⭐
5(\(f'(x) - 1\) 视作整体,\(f''(x)\) 视作这个整体的导数)⭐
6(乘积求导)⭐
7、8(乘开,视作乘积求导)⭐
9(乘开,对式子积分,然后分部积分拆开)⭐
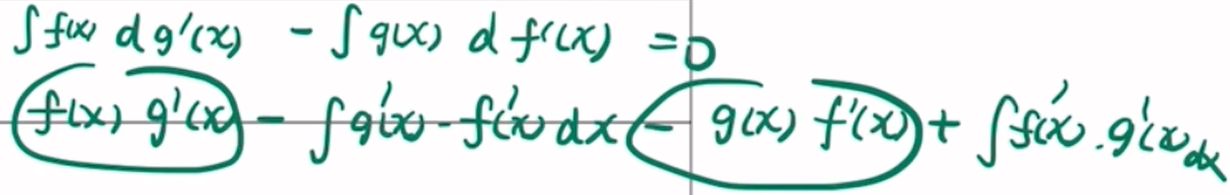


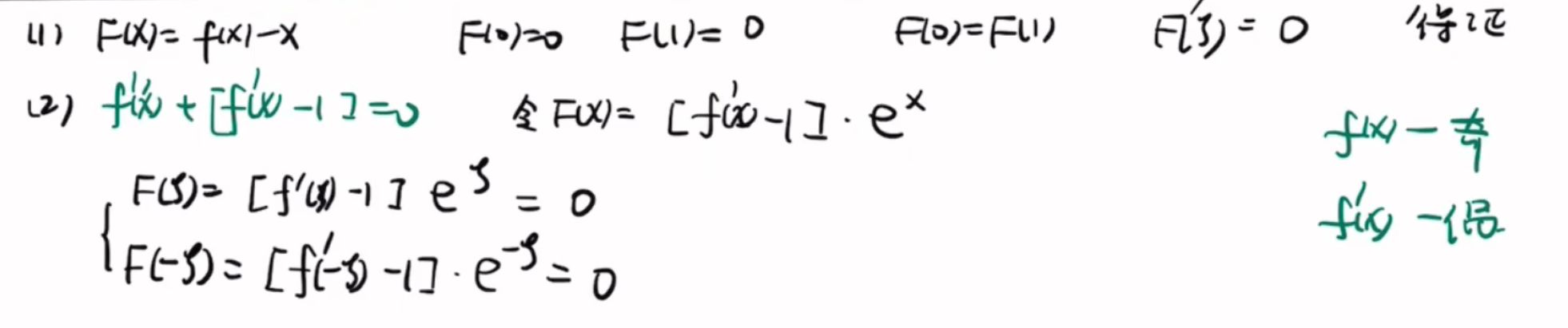

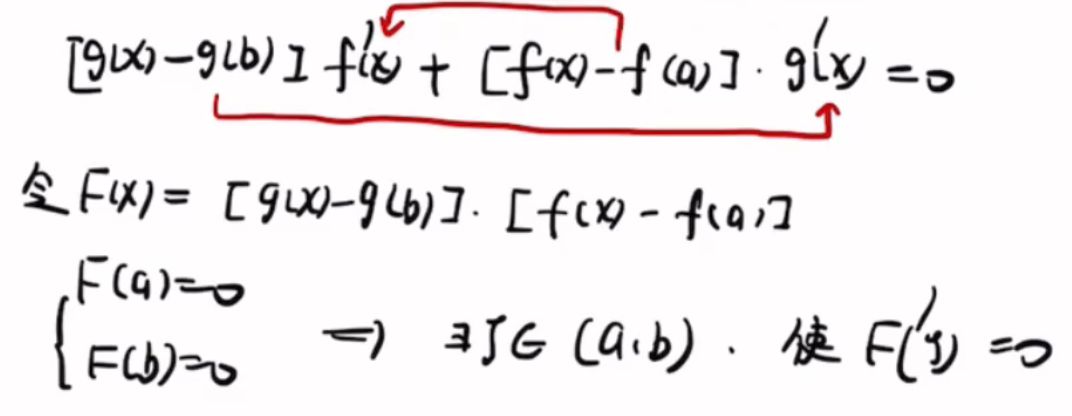


第一问,考虑罗尔构造原函数或者零点定理
第二问考虑找三个点相等的,罗尔
其中找第三个点采用极限保号性+零点定理




泰勒


介值定理
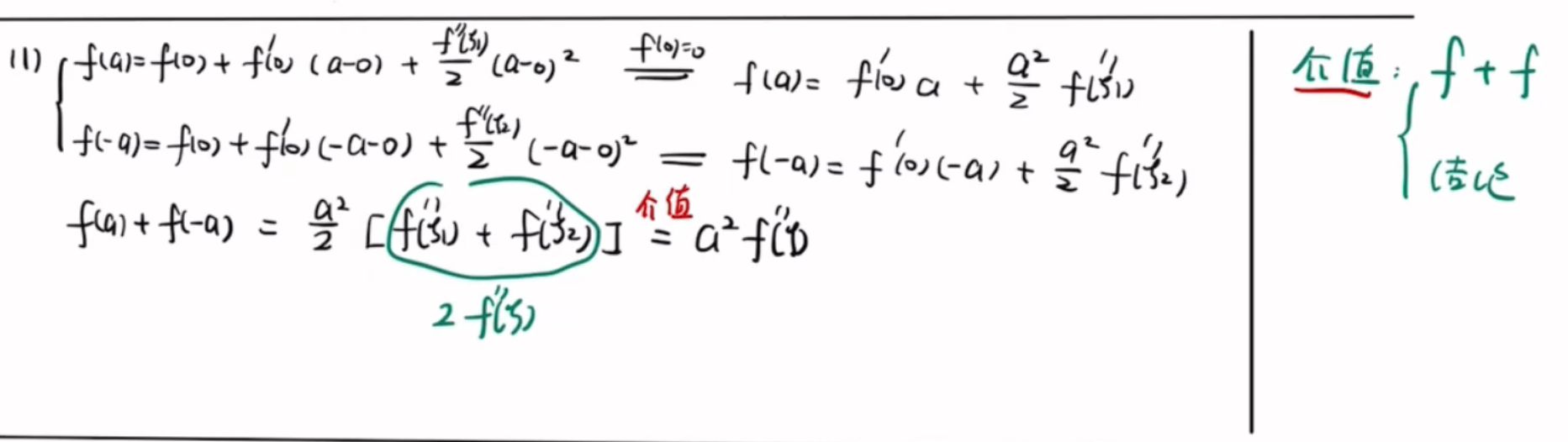

|a + b| <= |a| + |b|
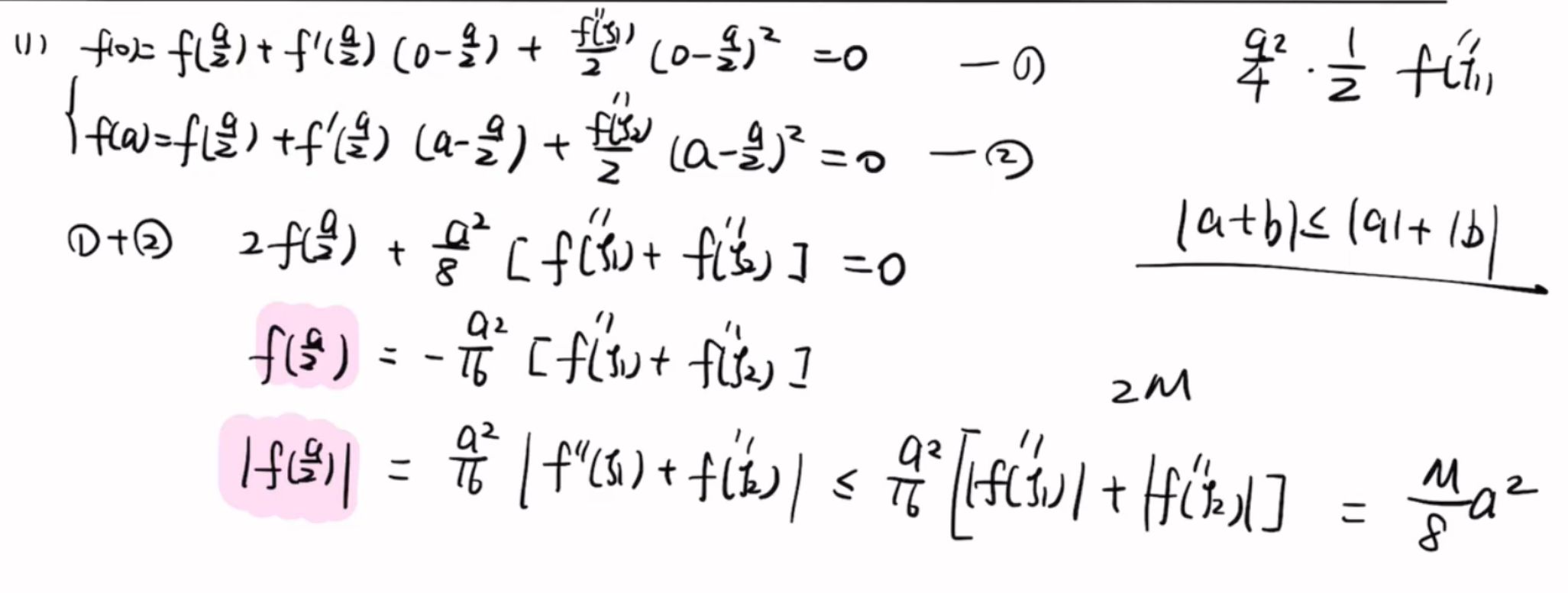


中值定理


不要求两中值不等
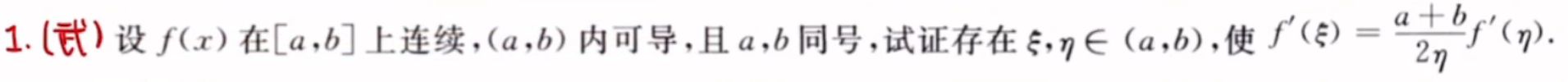

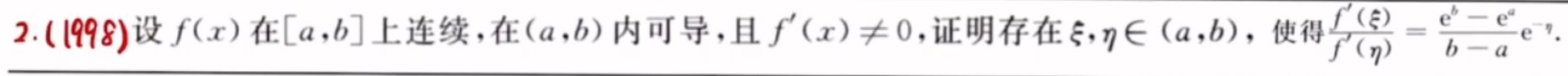
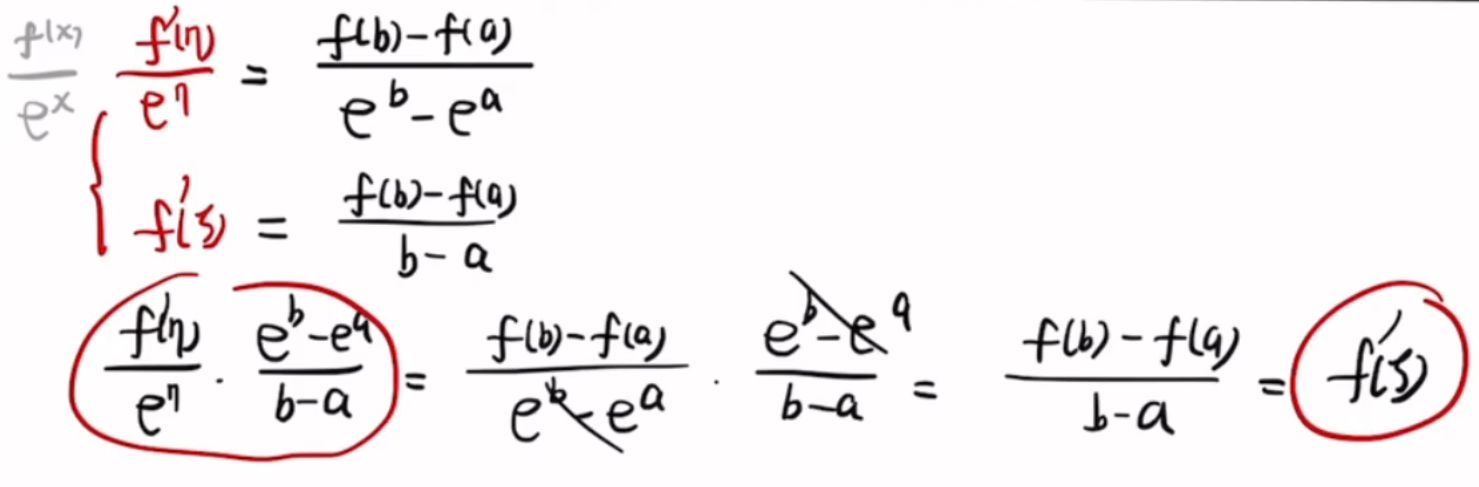
要求两点不等
找区间内一点设为 c,对划分出来的两个区间分别拉格朗日
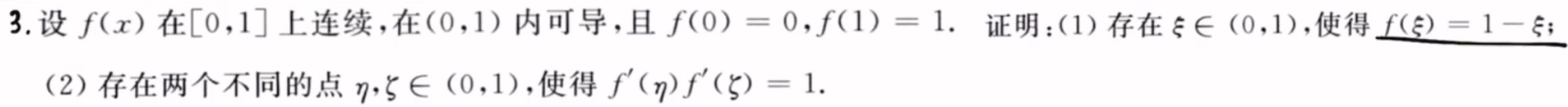
找交点

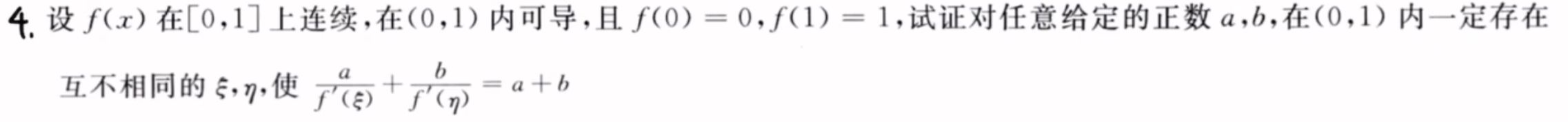

不等式

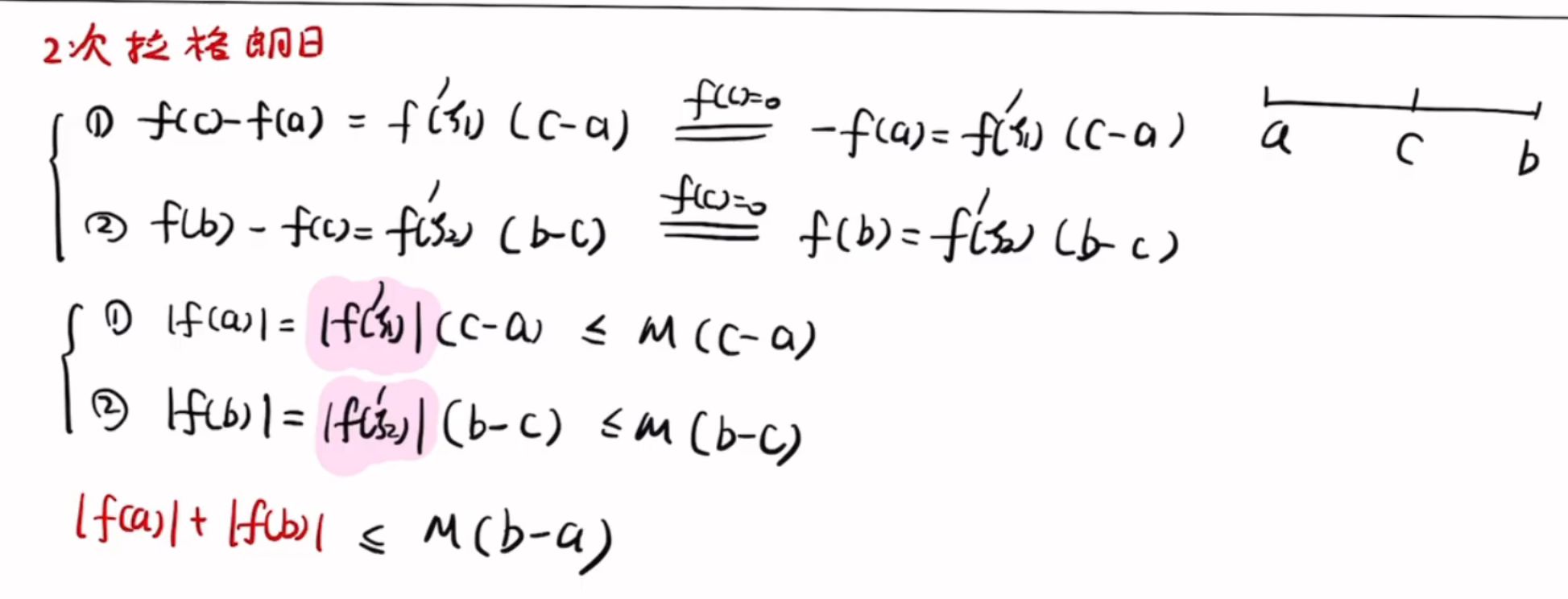


真题
泰勒×

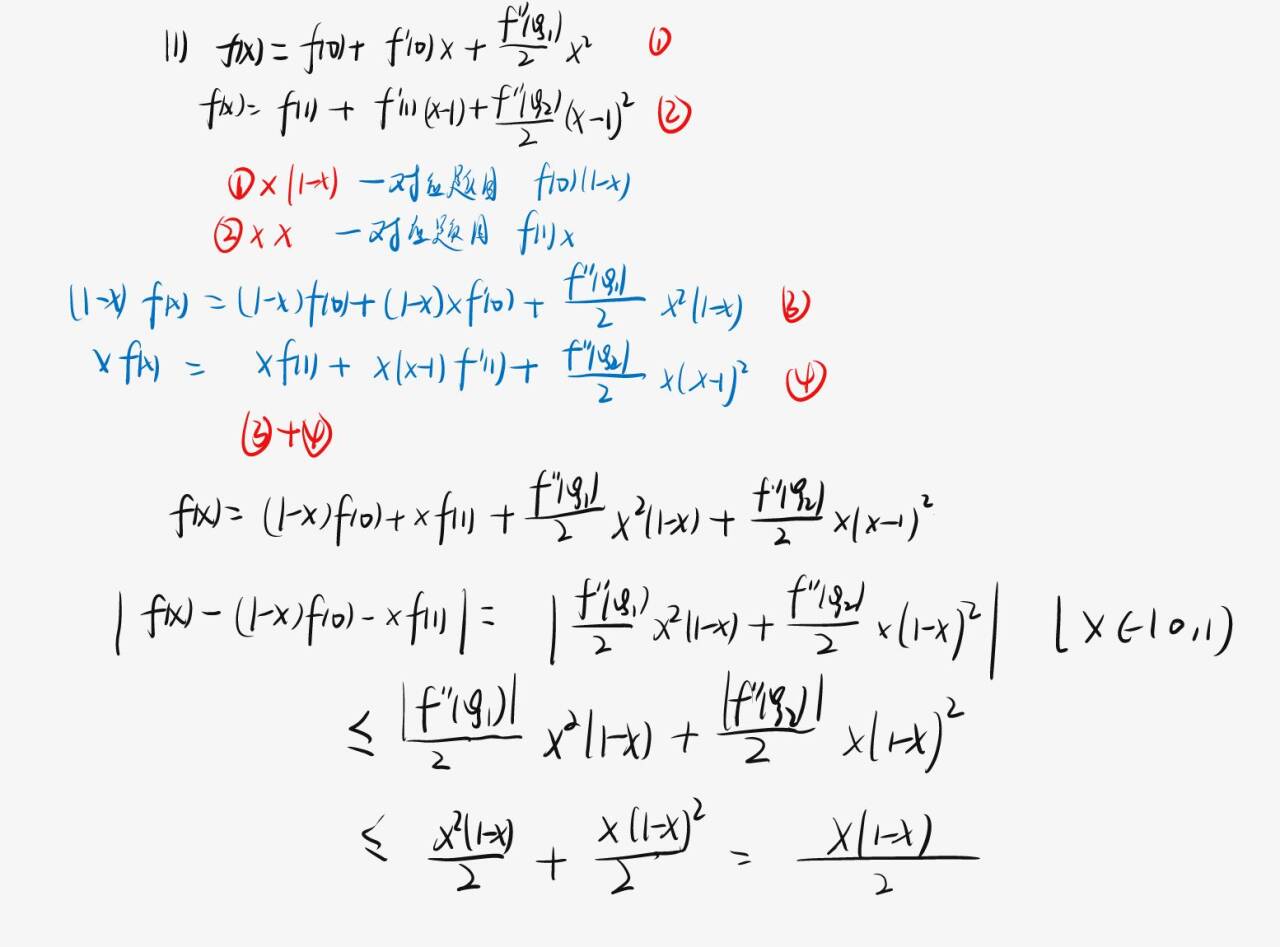
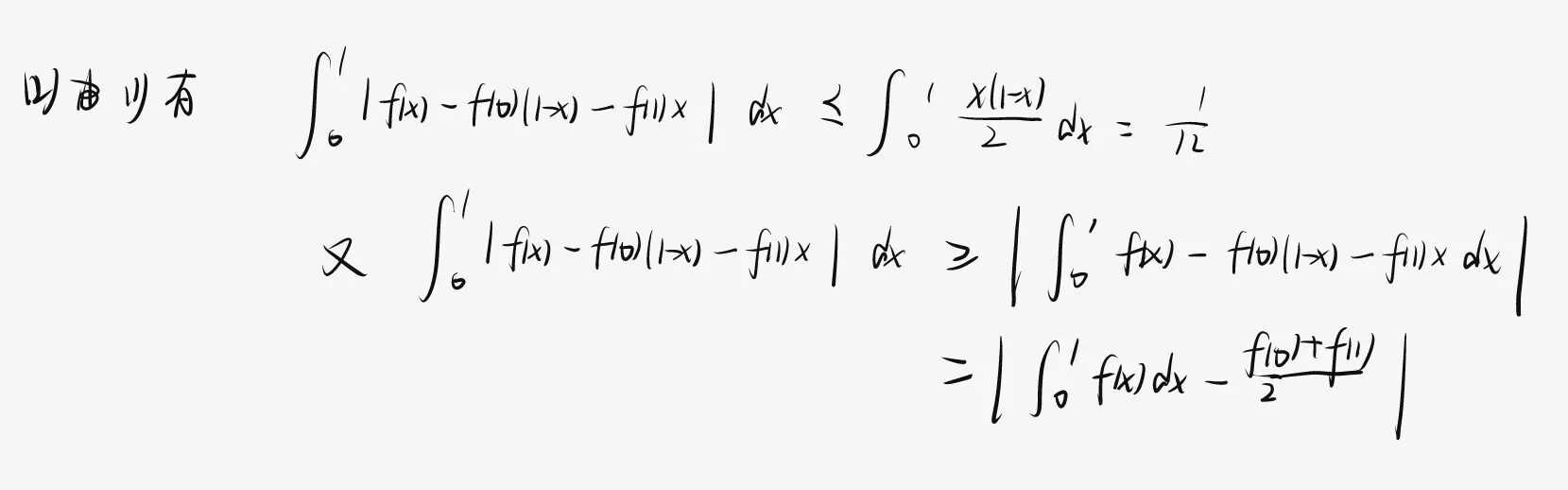
泰勒×

介值定理
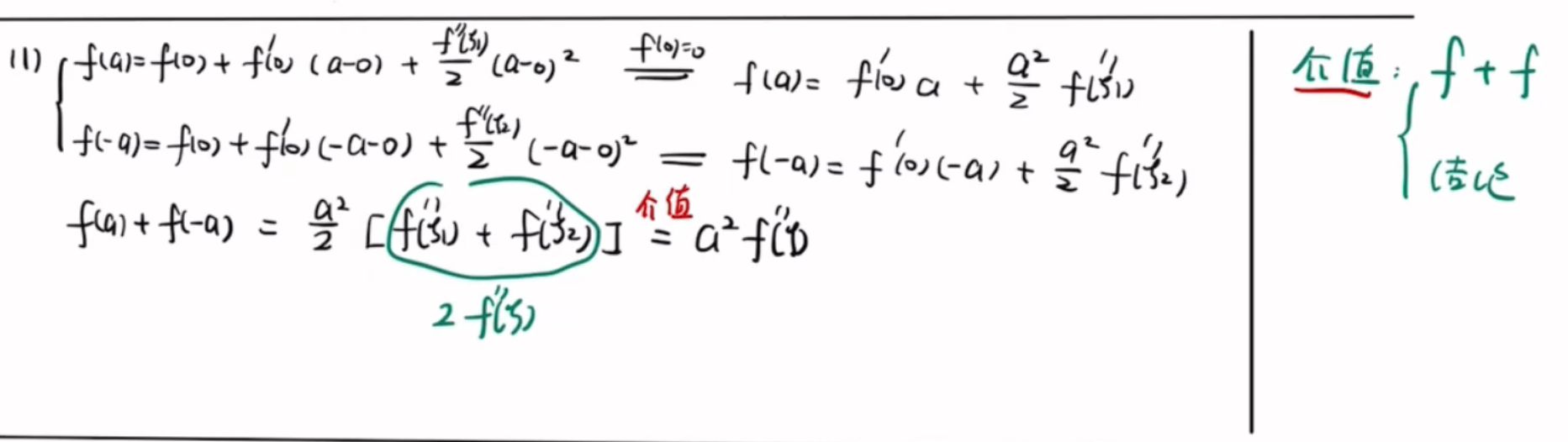
第二问说内部取极值,说明要在 极值点 c 展开

积分不等式×

看到积分不等式第一反应构造函数无脑求导
条件推结论是充分性
结论推条件是必要性
必要性

两个不同点相同,构造原函数,罗尔
对第二个积分分部积分,用积分中值定理
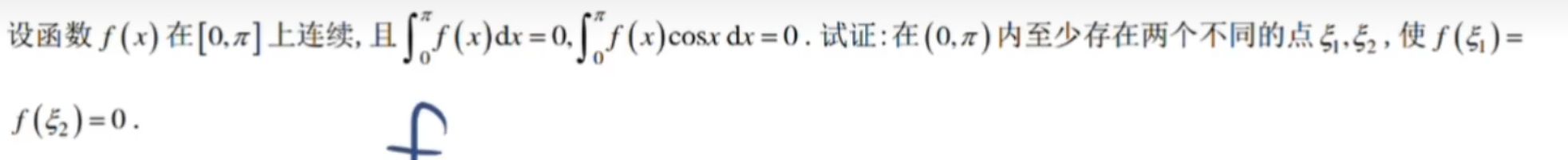

拉格朗日中值定理几何意义 (待补充)

柯西×




反证


泰勒然后凑导数定义
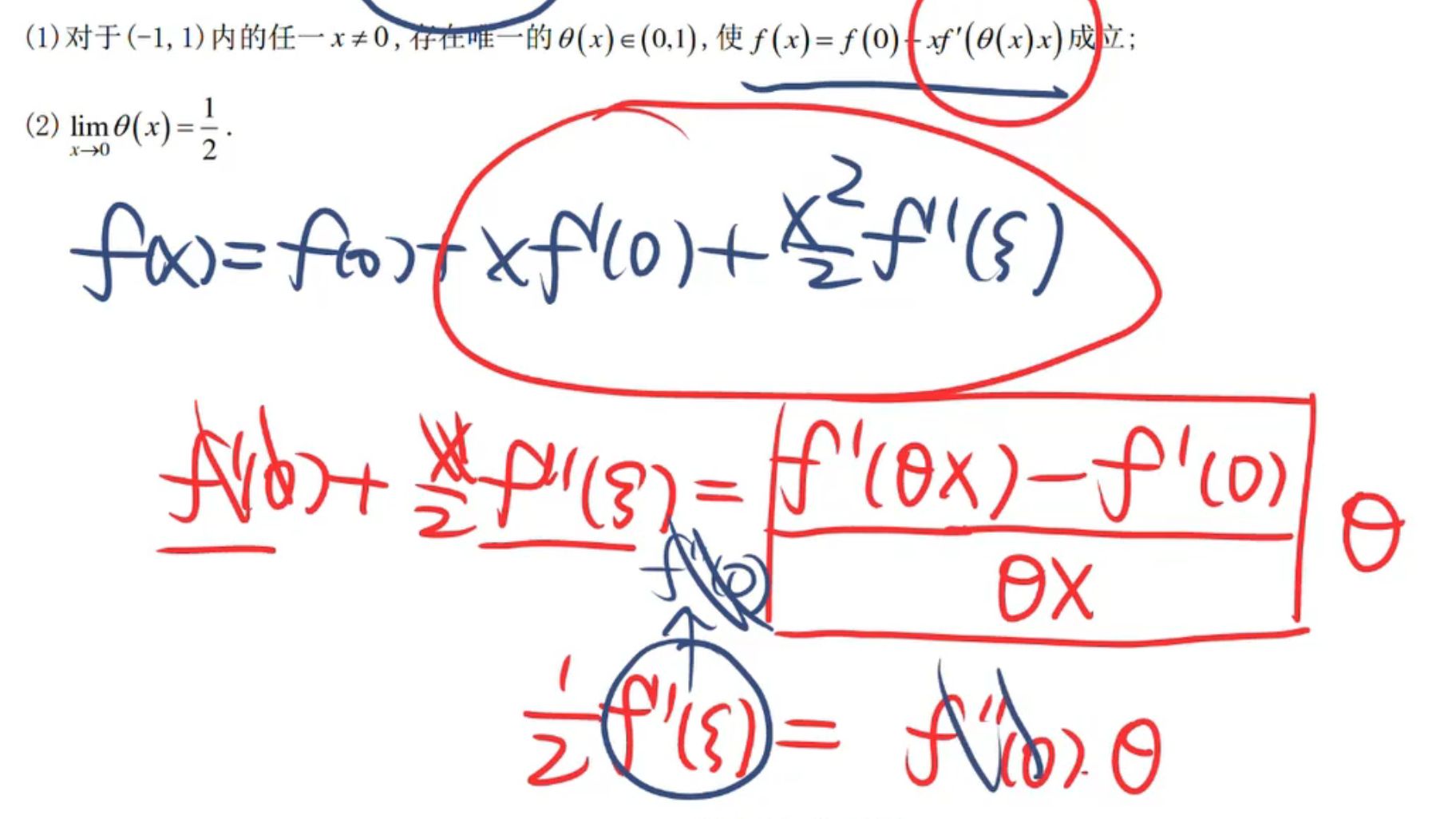


是两个不同的值
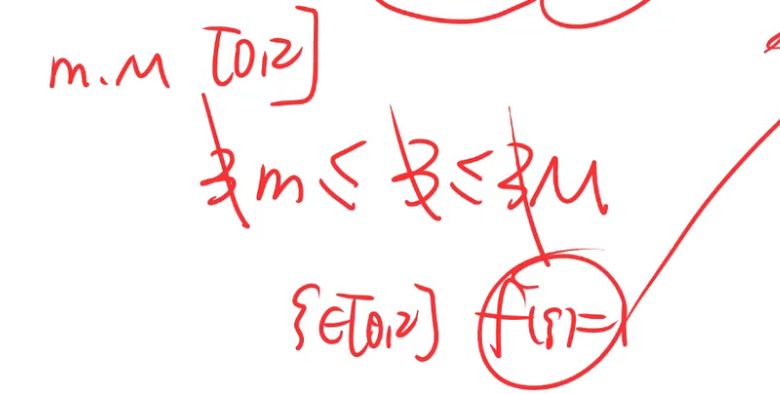
假设 一阶导 卡在 m,M之间,一阶导可以取到 m,M 之间任何一个数,这是对应前一个变量
证明 对f(x)积分也去证明卡在 m,M之间,这样 后面那个积分也可以取到 m,M 之间任何一个数
这时取两个不同值,可以让他相等

泰勒 ×

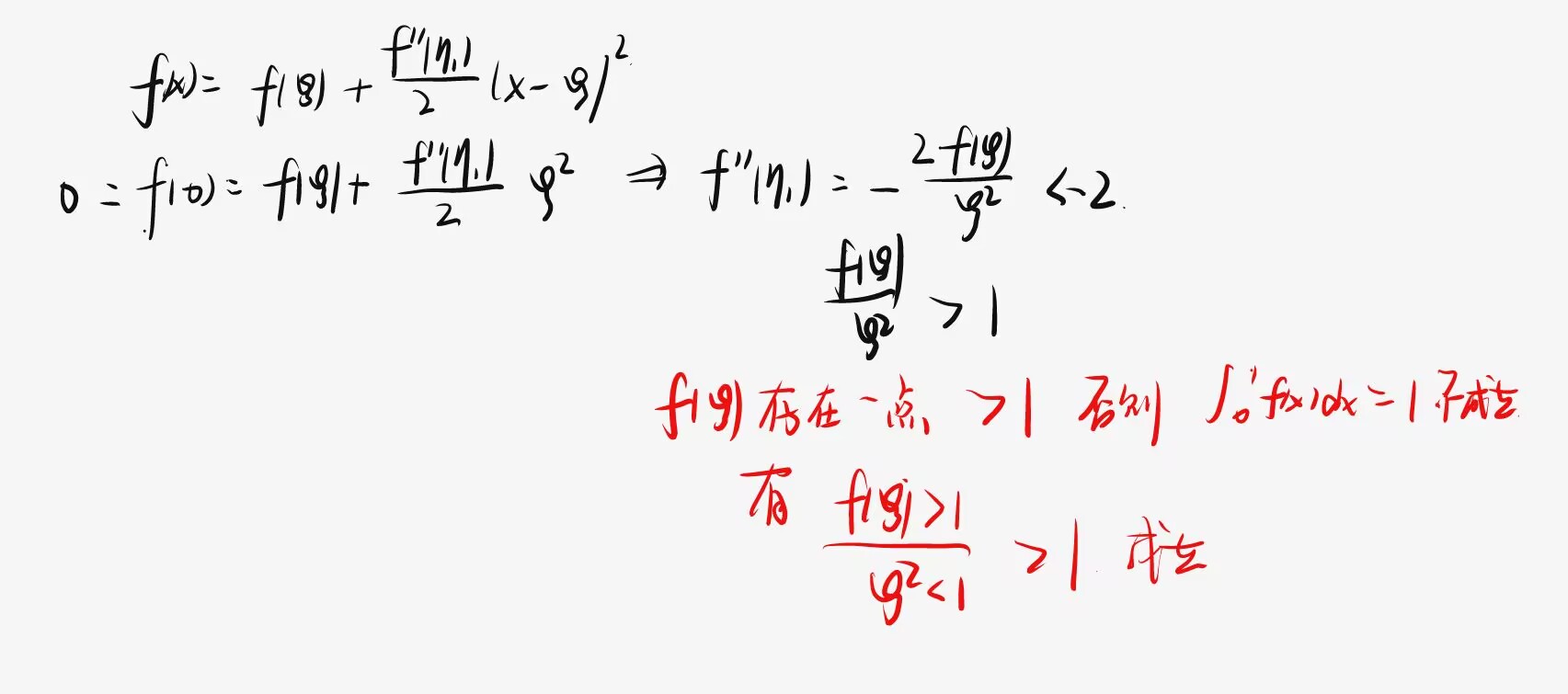
不是证明的证明

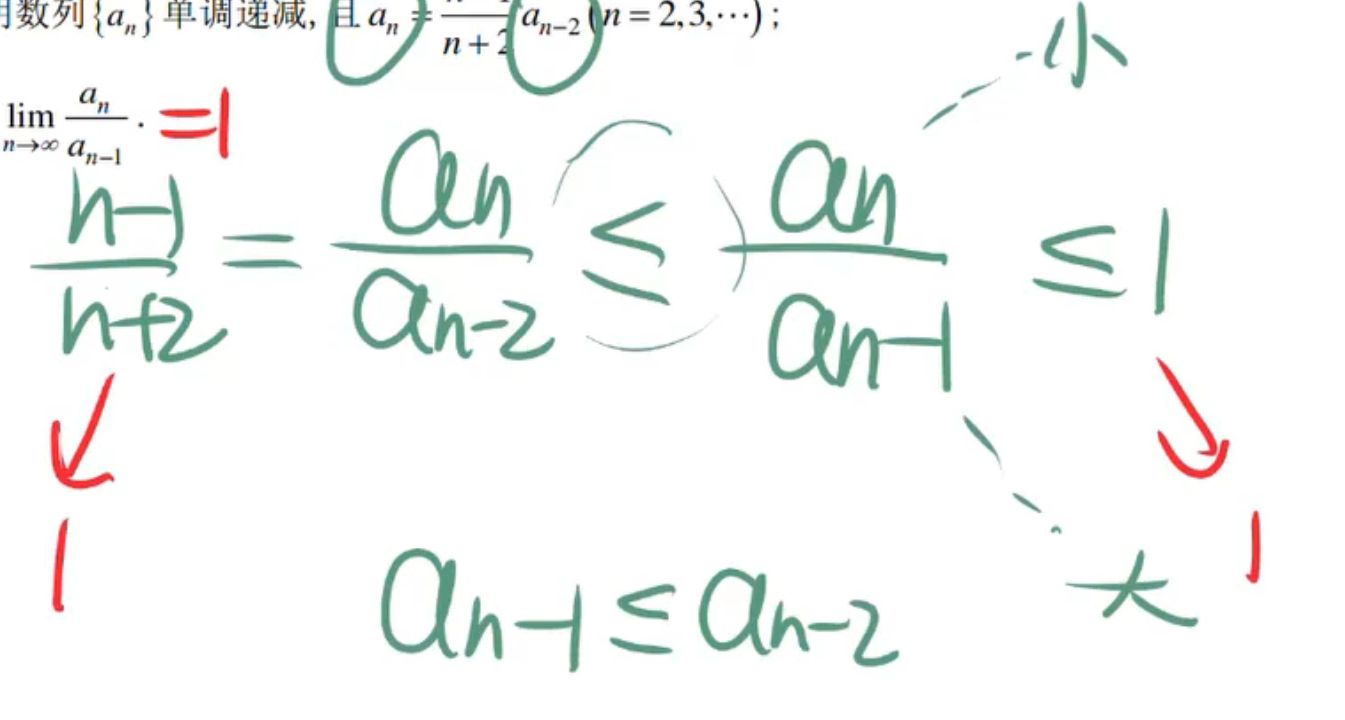
罗尔+构造函数
f(0) = 0
找一个导函数0点,两个原函数零点

藏零点

怪题

积分不等式
考虑变限积分求导就行

构造原函数

第一问用极限语言描述
第二问构造原函数
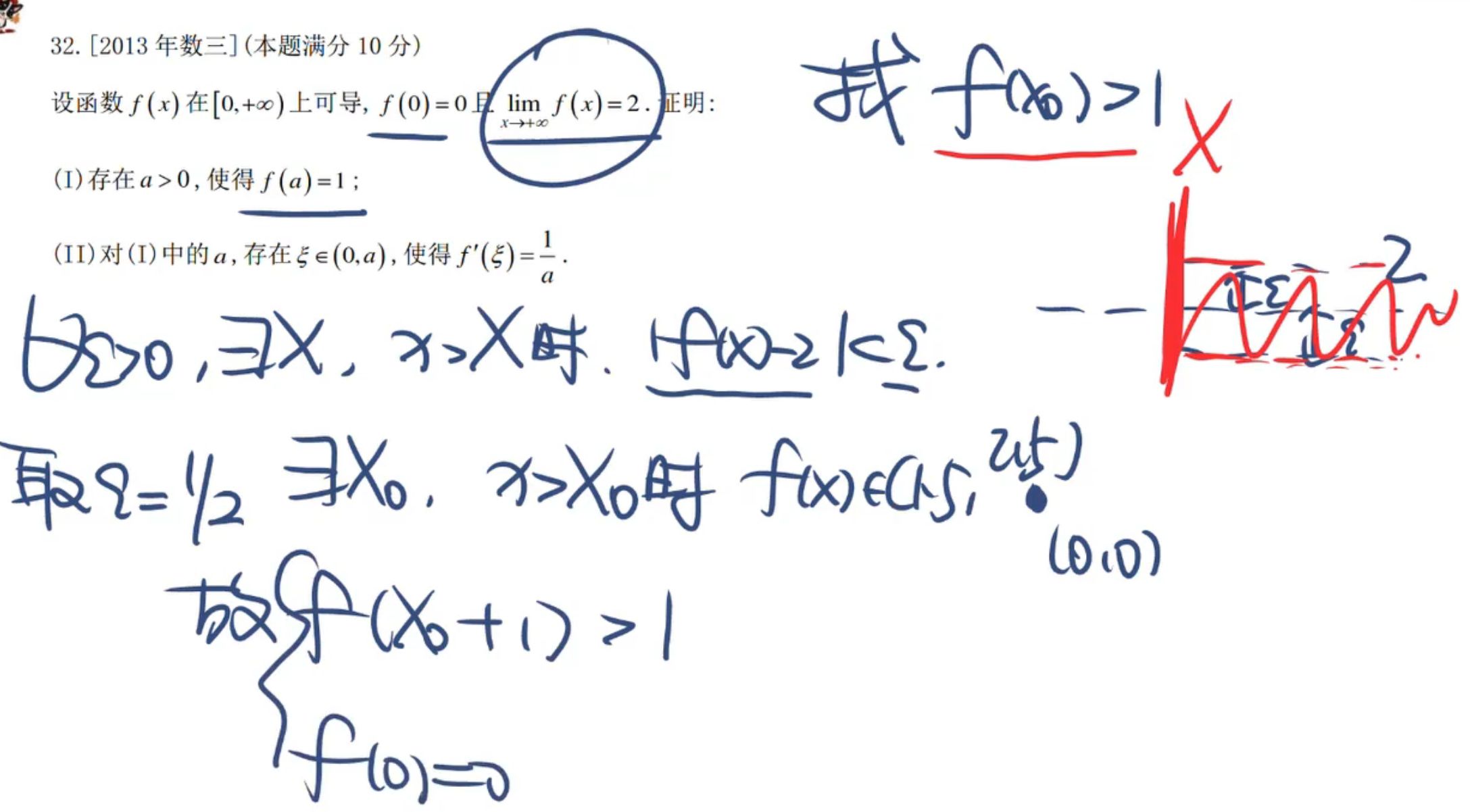
数列极限(ep原题)

第二问,随便找一个上界,xn取一个数使得 lnxn > 1
取极限不等号要变成等号

数列极限(ep原题)

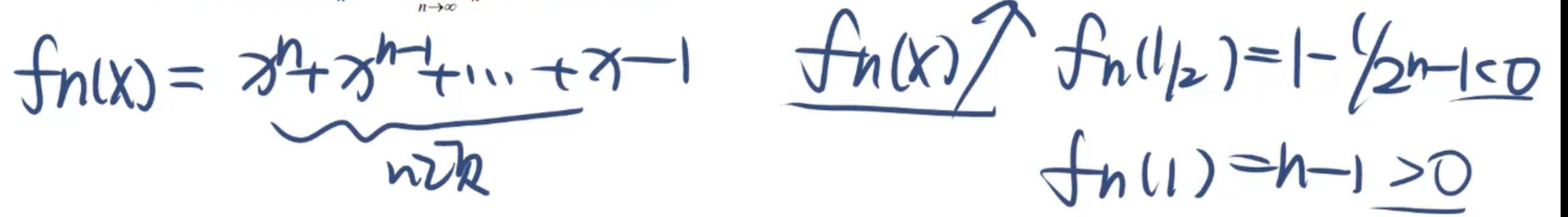
数列极限

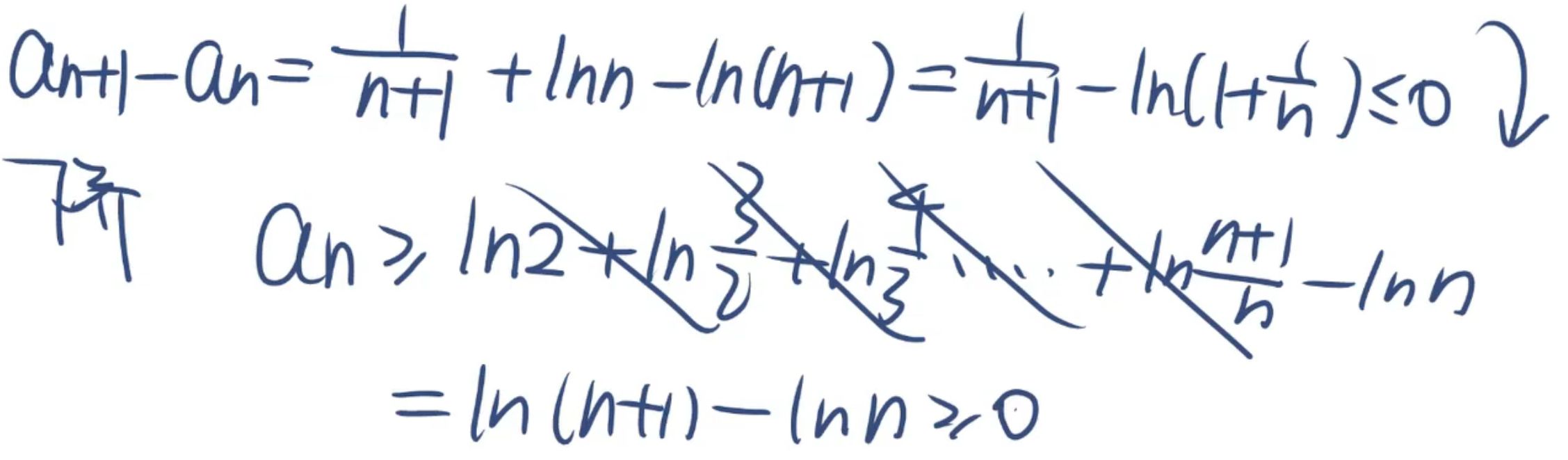
罗尔

2f(0) = f(2) + f(3) 如何转换?
用介值定理
双中值:构造函数 + 拉格朗日

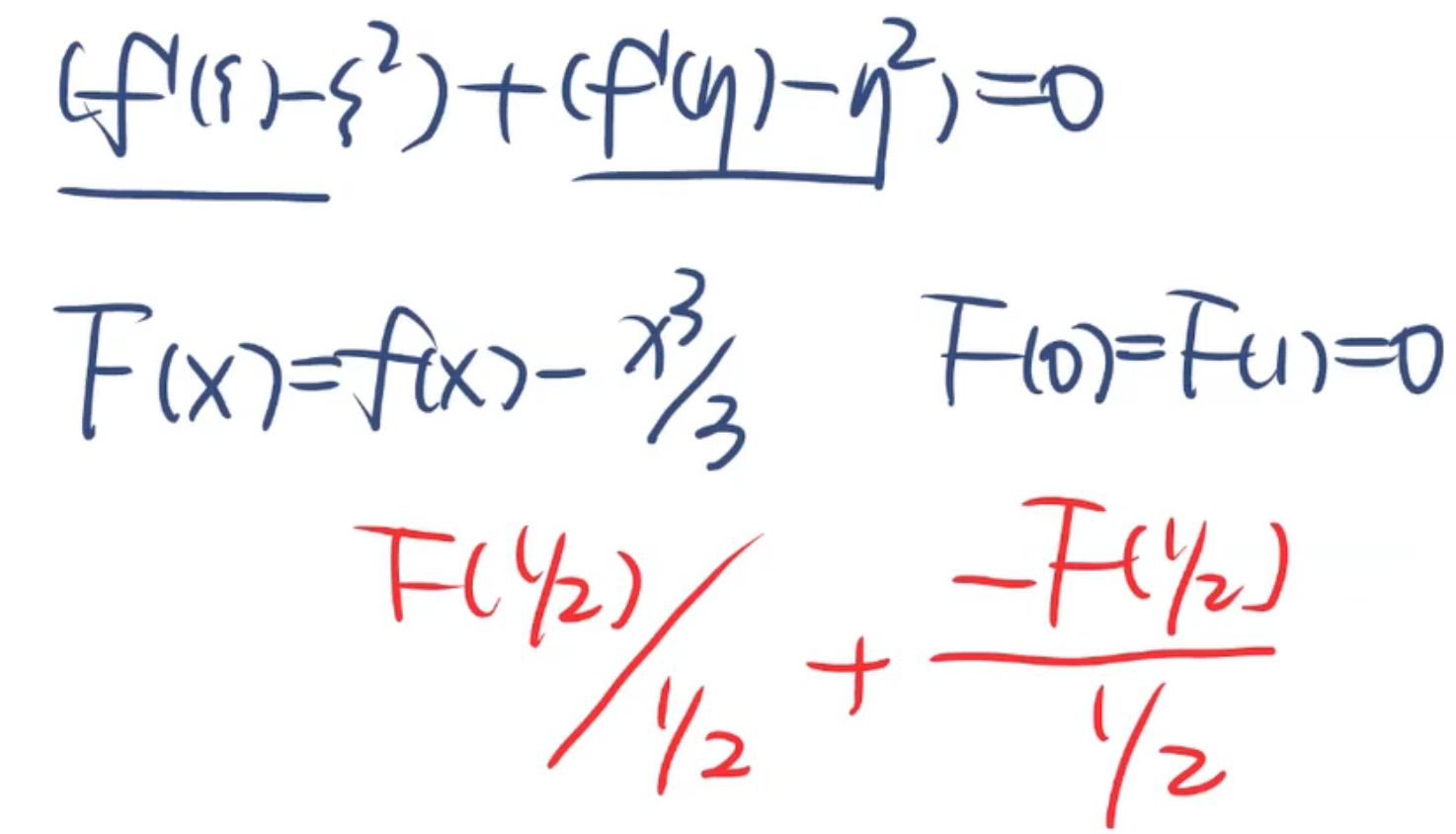
多次拉 + 零点定理


分情况讨论

分情况讨论f取最大值、g取最大值
同时取最大和不是同时取最大值

双中值:拉格朗日

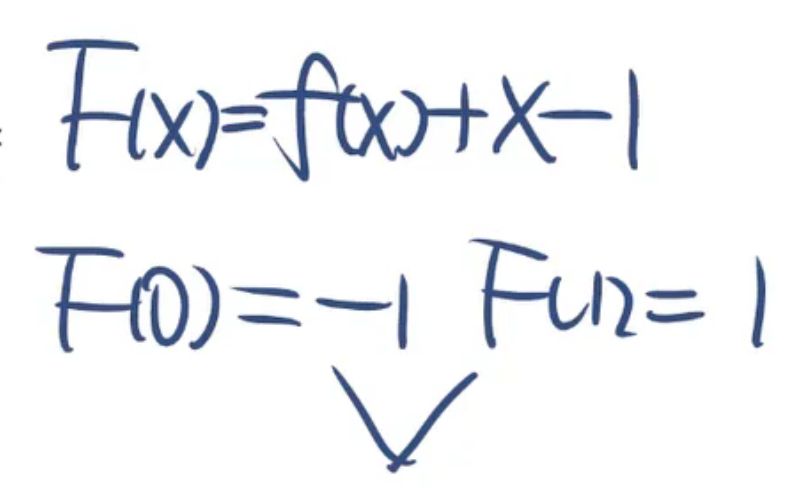
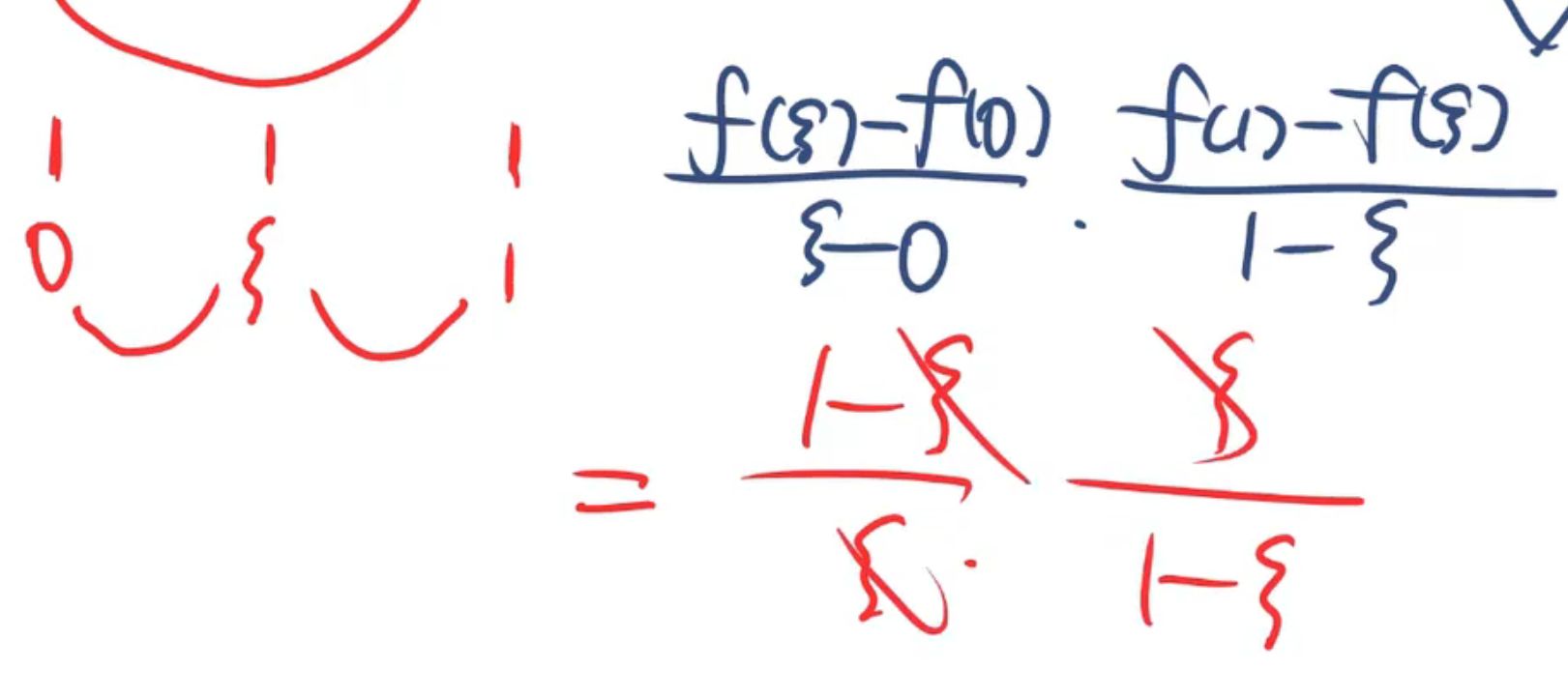
介值定理
物理应用
追击问题
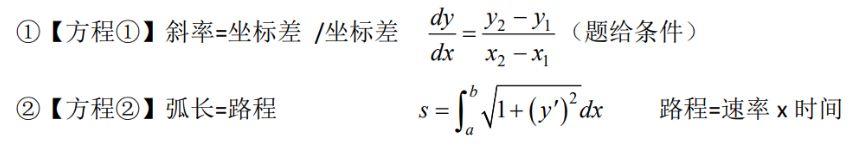
路程:速度对时间积分
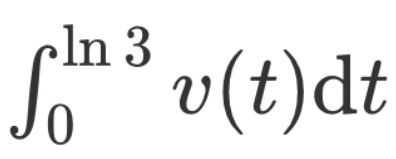
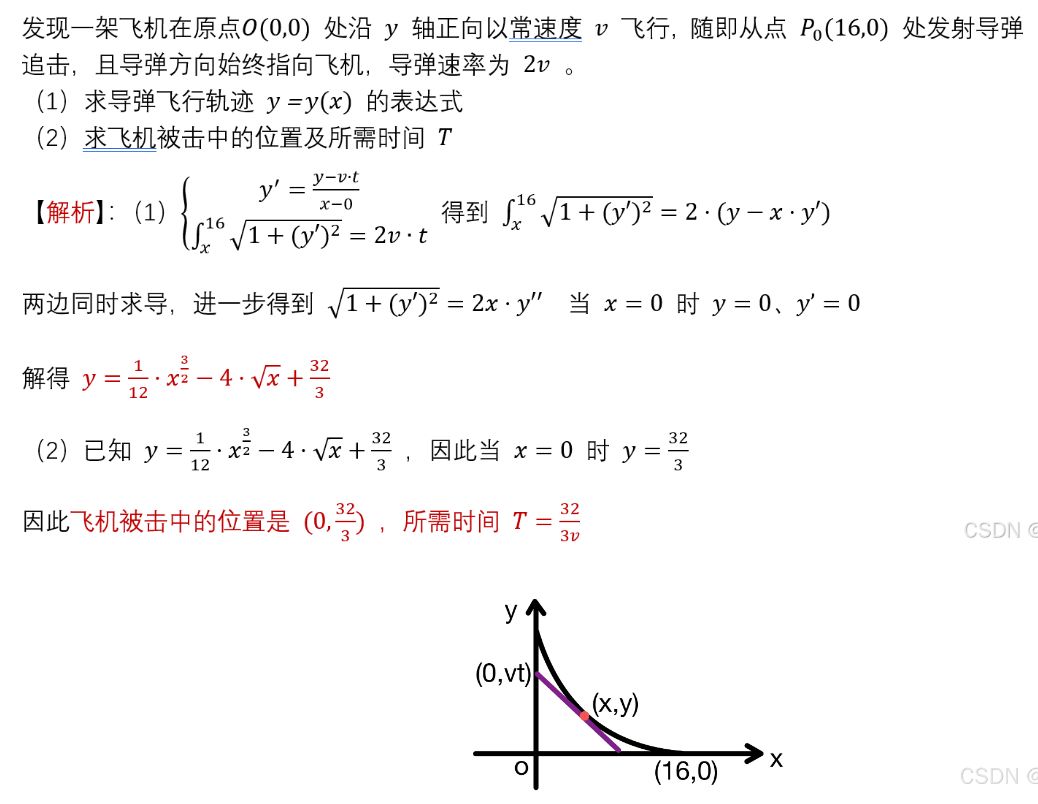



牛二
阻力记得加负号








变化率

注意:恒温


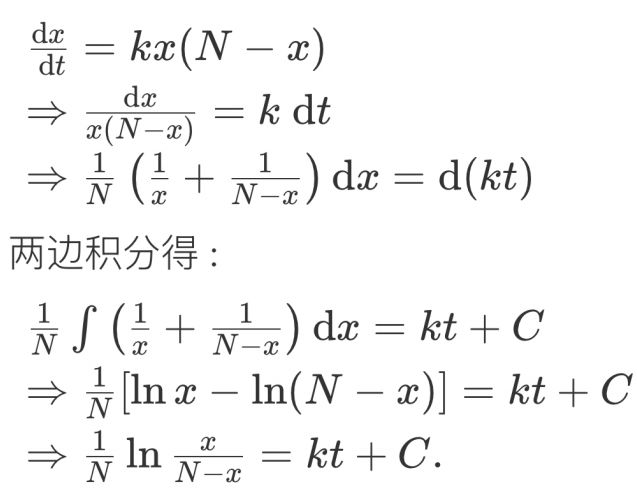




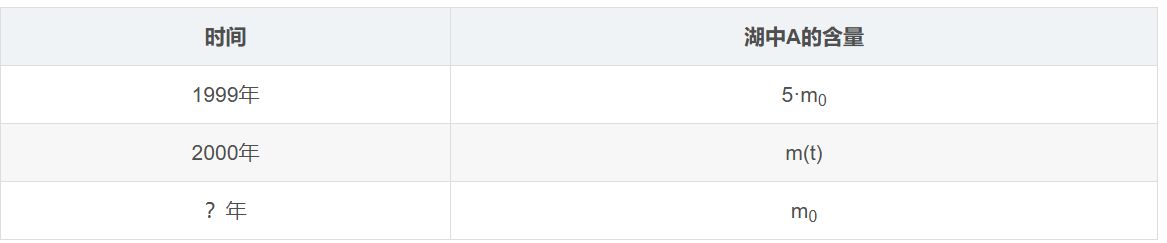
进出问题











 浙公网安备 33010602011771号
浙公网安备 33010602011771号