函数的极限和连续

函数的极限和连续

首先函数的极限有左右极限，极限存在的条件就是左右极限相等。连续就是加上 该点的值就是极限的值。还有一致连续的概念。

一些极限的题目，就是使用一些等价代换，洛必达还有泰勒展开。

下面这题我觉得第一种方法，技巧性太高了。所以写了第二种方法

这题是使用了函数和多阶导的有界性，证明中间的导函数的有界性。

下面这道题是求级数的，其实还可以转化成积分形式。

下面是很经典的导函数无第一类间断点，其实就是达布定理，导函数具有介值性。

这道题开始的时候，使用了夹逼准则，结果写错了。后面发现可以取对数，再使用stolz定理求解。

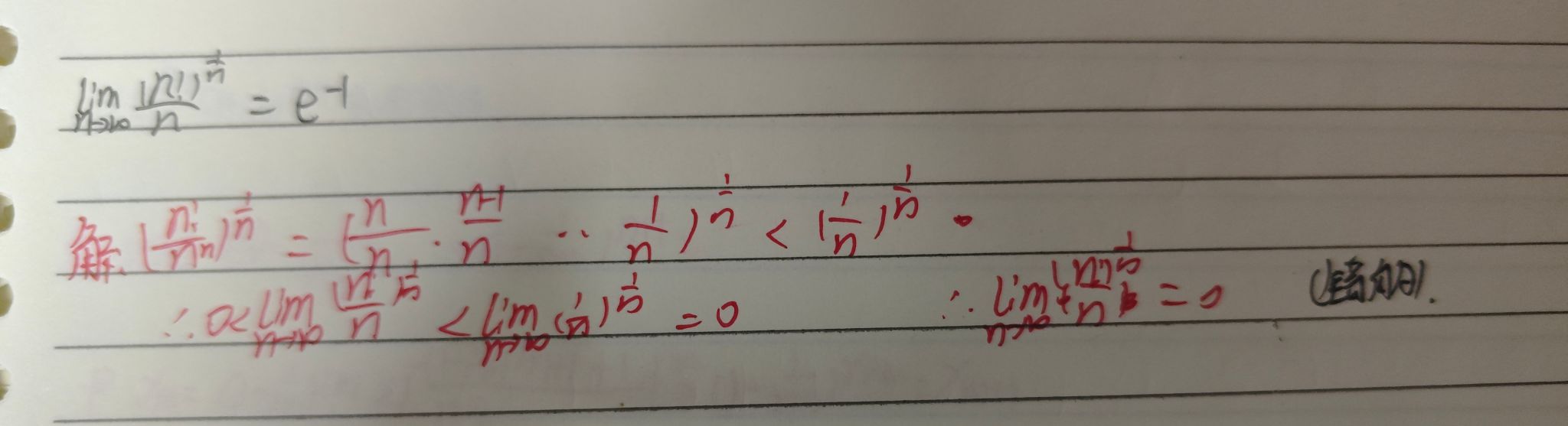
非常经典的证明黎曼函数在无理点连续，有理点不连续。