Luogu P6234 [eJOI 2019] T 形覆盖 题解 [ 紫 ] [ 图论建模 ] [ 分类讨论 ] [ 基环树 ]
场上没有注意到转化,对着基环树和树的部分暴力图论建模,爆肝 3h 大分讨以 7.88KB 的代码成功通过。
Sol.1 暴力分讨
下文中,我们称 T 形的中心为黑点,其余格子为白点。
从部分分做法开始想,当 \(\min dis\le 2\) 的时候:

容易发现,有影响的结构有三种:
- 切比雪夫距离为 \(1\),斜角放置。
- 切比雪夫距离为 \(1\),横行 / 纵列放置。
- 切比雪夫距离为 \(2\),横行 / 纵列放置。
无影响的结构有两种,除了横行 / 纵列放置的以外切比雪夫距离等于 \(\bm 2\) 的全是没有影响的。手模可以发现,当切比雪夫距离大于 \(2\) 时,无论怎么摆放两者之间均无影响。
注意到切比雪夫距离为 \(\bm 1\) 的结构合法的覆盖范围一定唯一,我们显然可以特判掉。考虑切比雪夫距离为 \(2\) 且横行 / 纵列放置的怎么处理。我们先对连成整段的考虑,如下图:
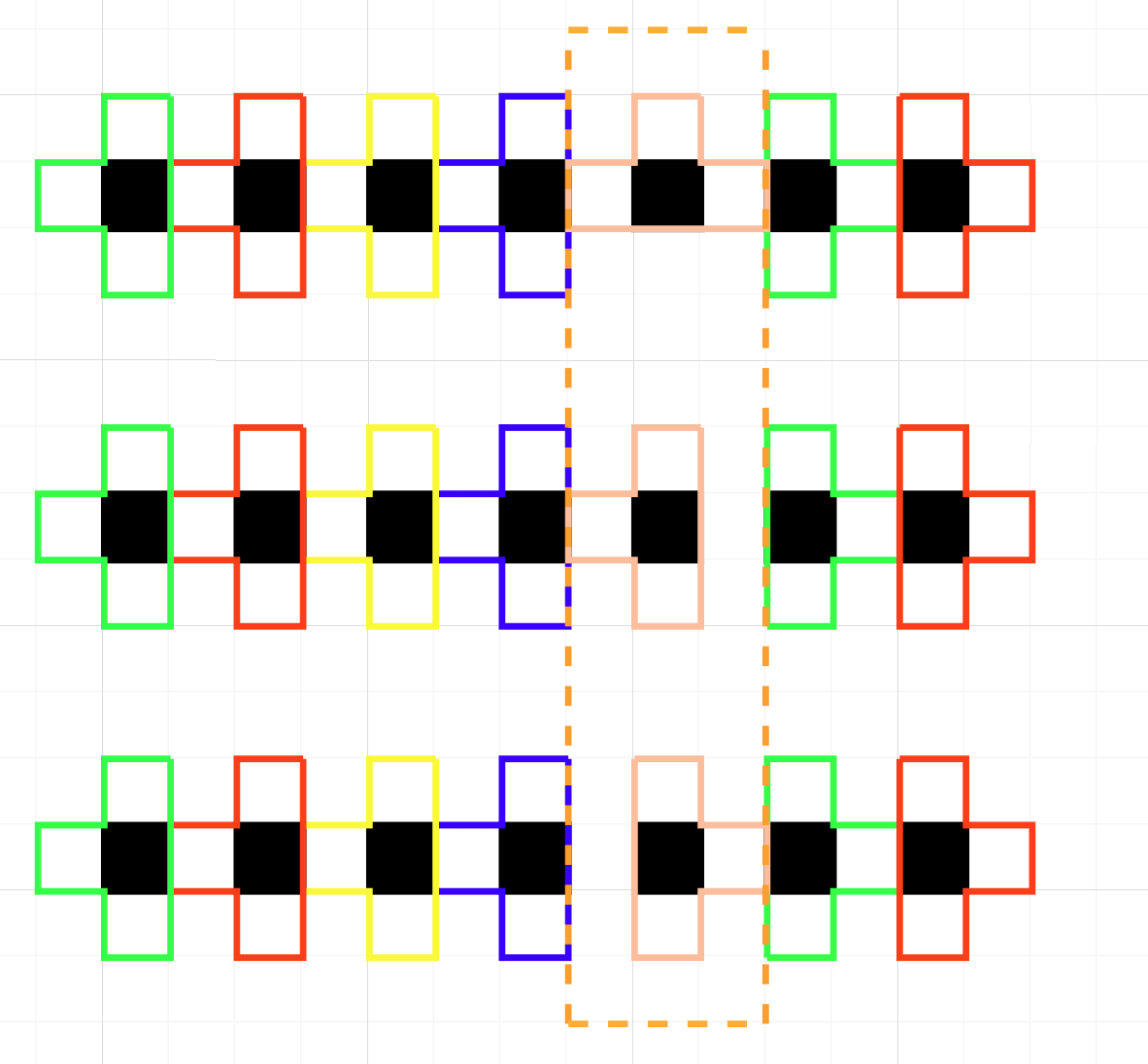
发现当改变框内的 T 形朝向,并强制要求十字架空出来的那一格不被覆盖时,会导致左右两侧的 T 形方向全部被确定。于是我们考虑图论建模,对切比雪夫距离为 \(2\) 且横行 / 纵列放置的两个点之间连一条边。则上述我们考虑的情况就变成了一条链。
而对于树 / 基环树 / 一般图的情况,可以见下图:

因为基环树 / 一般图的构造方案画出来太复杂了,这里可能需要读者自己手模。总之就是容易发现,基环树上覆盖的范围一定是唯一的,是所有黑点曼哈顿距离不超过 \(\bm{1}\) 的邻域之并;而如果图上存在多个环,那么这种情况一定无解。
对于一般树的情况,我们发现这和链的情况是差不多的,都是钦定了一个 T 形的方向,然后其余 T 形的方向也随之确定了。
于是用并查集维护连通块内的边数,根据边数判断连通块的类型:
- 一般图:直接无解。
- 基环树:所有黑点曼哈顿距离不超过 \(1\) 的邻域之并。
- 普通树:先求出所有黑点曼哈顿距离不超过 \(1\) 的邻域之并,然后删掉连通块内的最小值即可,因为总是要钦定掉一个 T 形的方向的。
注意特判四个边界与其余两个有影响的结构对基环树 / 普通树的影响,如果基环树被他们影响了(邻域与被影响的区域有交),则直接无解;如果树被他们影响了(邻域与被影响的区域有交),则变成基环树的处理方式。
就此模拟,若视并查集为线性,则时间复杂度为 \(O(n)\)。
下面为考场代码,脑子可能不是很清晰,细节也可能与上述做法不同。
#include <bits/stdc++.h>
using namespace std;
const int N = 1000005, inf = 0x3f3f3f3f;
const int gox1[] = {1, 0};
const int goy1[] = {0, 1};
const int gox2[] = {-1, 0, 0, 1, 1, 2};
const int goy2[] = {0, -1, 1, -1, 1, 0};
const int gox3[] = {-1, -1, 0, 0, 1, 1};
const int goy3[] = {0, 1, -1, 2, 0, 1};
const int gox4[] = {1, 1};
const int goy4[] = {1, -1};
const int gox5[] = {-1, 0, 0, 1, 1, 2};
const int goy5[] = {0, -1, 1, 0, 2, 1};
const int gox6[] = {-1, 0, 0, 1, 1, 2};
const int goy6[] = {0, -1, 1, -2, 0, -1};
const int gox7[] = {-2, 2, 0, 0};
const int goy7[] = {0, 0, -2, 2};
const int gox8[] = {-1, 1, 0, 0};
const int goy8[] = {0, 0, -1, 1};
const int goys[] = {1, 0, 3, 2};
int n, m, a[N], ans;
bitset<N> b, ban, con;
int h[N], eidx;
struct Edge{
int v, ne, frm;
} e[2 * N];
void add(int u, int v, int frm)
{
e[++eidx] = {v, h[u], frm};
h[u] = eidx;
}
bool legal(int x, int y)
{
return (0 <= x && x < n && 0 <= y && y < m);
}
int getid(int x, int y)
{
return x * m + y;
}
void nosol()
{
cout << "No";
exit(0);
}
struct DSU{
int fa[N], tag[N];
void init()
{
for(int i = 0; i < N; i++) fa[i] = i;
}
int findf(int x)
{
if(fa[x] != x) fa[x] = findf(fa[x]);
return fa[x];
}
void combine(int x, int y)
{
int fx = findf(x), fy = findf(y);
if(fx == fy) return;
fa[fx] = fy;
tag[fy] += tag[fx];
if(tag[fx] >= 2) nosol();
}
} dsu;
void Case1()
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
{
if(b[getid(i, j)] == 0) continue;
for(int p = 0; p < 2; p++)
{
int tx = i + gox1[p], ty = j + goy1[p];
if(!legal(tx, ty)) continue;
if(b[getid(tx, ty)] == 0) continue;
if(p == 0)
{
for(int k = 0; k < 6; k++)
{
int kx = i + gox2[k], ky = j + goy2[k];
if(!(legal(kx, ky) && ban[getid(kx, ky)] == 0)) nosol();
ban[getid(kx, ky)] = 1;
ans += a[getid(kx, ky)];
con[getid(kx, ky)] = 1;
}
}
else
{
for(int k = 0; k < 6; k++)
{
int kx = i + gox3[k], ky = j + goy3[k];
if(!(legal(kx, ky) && ban[getid(kx, ky)] == 0)) nosol();
ban[getid(kx, ky)] = 1;
ans += a[getid(kx, ky)];
con[getid(kx, ky)] = 1;
}
}
con[getid(i, j)] = con[getid(tx, ty)] = 1;
}
}
}
}
void Case2()
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
{
if(b[getid(i, j)] == 0) continue;
for(int p = 0; p < 2; p++)
{
int tx = i + gox4[p], ty = j + goy4[p];
if(!legal(tx, ty)) continue;
if(b[getid(tx, ty)] == 0) continue;
if(p == 0)
{
for(int k = 0; k < 6; k++)
{
int kx = i + gox5[k], ky = j + goy5[k];
if(!(legal(kx, ky) && ban[getid(kx, ky)] == 0)) nosol();
ban[getid(kx, ky)] = 1;
ans += a[getid(kx, ky)];
con[getid(kx, ky)] = 1;
}
}
else
{
for(int k = 0; k < 6; k++)
{
int kx = i + gox6[k], ky = j + goy6[k];
if(!(legal(kx, ky) && ban[getid(kx, ky)] == 0)) nosol();
ban[getid(kx, ky)] = 1;
ans += a[getid(kx, ky)];
con[getid(kx, ky)] = 1;
}
}
con[getid(i, j)] = con[getid(tx, ty)] = 1;
}
}
}
}
void Build_Graph()
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
{
int u = getid(i, j);
if(b[u] == 0) continue;
for(int p = 0; p < 4; p++)
{
int tx = i + gox7[p], ty = j + goy7[p];
int v = getid(tx, ty);
if(!legal(tx, ty)) continue;
if(b[v] == 0) continue;
if(con[u] || con[v]) continue;
if(u < v)
{
add(u, v, p);
add(v, u, goys[p]);
if(dsu.findf(u) == dsu.findf(v))
{
if(dsu.tag[dsu.findf(u)]) nosol();
dsu.tag[dsu.findf(u)]++;
}
else dsu.combine(getid(i, j), getid(tx, ty));
}
}
}
}
}
void Case3()
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
{
int u = getid(i, j);
int anc = dsu.findf(u);
if(!dsu.tag[anc]) continue;
for(int k = 0; k < 4; k++)
{
int tx = i + gox8[k], ty = j + goy8[k];
if(!legal(tx, ty)) nosol();
int v = getid(tx, ty);
if(ban[v]) nosol();
if(con[v]) continue;
ans += a[v];
con[v] = 1;
}
}
}
}
int fsm[N], fmx[N], qd[N];
void Case4()
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
{
int u = getid(i, j);
int anc = dsu.findf(u);
if(dsu.tag[anc]) continue;
if(con[u]) continue;
if(!b[u]) continue;
for(int k = 0; k < 4; k++)
{
int tx = i + gox8[k], ty = j + goy8[k];
if(!legal(tx, ty))
{
qd[anc]++;
if(qd[anc] >= 2) nosol();
continue;
}
int v = getid(tx, ty);
if(ban[v])
{
if(qd[anc] >= 2) nosol();
qd[anc]++;
continue;
}
if(con[v]) continue;
fsm[anc] += a[v];
con[v] = 1;
}
}
}
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
{
int u = getid(i, j);
int anc = dsu.findf(u);
if(qd[anc] == 1)
{
if(u == anc) ans += fsm[u];
continue;
}
if(dsu.tag[anc]) continue;
if(con[u]) continue;
if(!b[u]) continue;
multiset<int> s;
ans -= fmx[anc];
int res = fsm[anc];
for(int k = 0; k < 4; k++)
{
int tx = i + gox8[k], ty = j + goy8[k];
int v = getid(tx, ty);
res -= a[v];
s.insert(a[v]);
}
for(int k = 0; k < 3; k++)
{
auto it = prev(s.end());
res += *it;
s.erase(it);
}
fmx[anc] = max(fmx[anc], res);
ans += fmx[anc];
}
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
dsu.init();
cin >> n >> m;
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
cin >> a[getid(i, j)];
int kcnt;
cin >> kcnt;
while(kcnt--)
{
int x, y;
cin >> x >> y;
b[getid(x, y)] = ban[getid(x, y)] = 1;
ans += a[getid(x, y)];
}
// dis = 1, 直接相邻
Case1();
// dis = 1, 斜角相邻
Case2();
// dis = 2, 直接横向, 不考虑斜向
// 建图
Build_Graph();
// 基环树,直接确定所有点
Case3();
// 普通树
Case4();
cout << ans;
return 0;
}
Sol.2 图论转化
第一篇题解叽里咕噜说什么呢,感觉 StudyingFather 讲的才是最简单的啊。
前几步是一样的,都是从有 / 无影响的结构入手。只是要从“删去十字架内的一个角”的角度考虑问题,然后将有影响的结构全部连边,形成一个连通块。令连通块内白点的个数为 \(S\),接下来我们对每个连通块内的黑点个数 \(x\) 分别讨论:
- 当 \(S < 3x\) 时,无解。因为一个黑点对应匹配了 \(\bm{3}\) 个互不相同的白点。
- 当 \(S = 3x\) 时,每个黑点恰好匹配了三个互不相同的白点,答案即为连通块内点权之和。
- 当 \(S = 3x+1\) 时,答案即为连通块内点权之和减去最小的点权。
使用并查集维护,时间复杂度为 \(O(n)\),代码被简化了很多,但是我懒了,没写。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号