Luogu P5904 [POI 2014] HOT-Hotels 加强版 题解 [ 紫 ] [ 树形 DP ] [ 长链剖分 ] [ 指针 ]

[POI 2014] HOT-Hotels 加强版：长链剖分优化 DP 的神秘题。

对于长剖优化 DP 相关题，一般都是对每个点多设一个关于与该节点的距离的维度，或者是可以直接从子节点经过下标平移后得到的维度。并且注意每个状态只能存一个值，不能有多个。

长剖优化 DP 题一般都是想出一个 \(O(n^2)\) 的 DP 再去优化，因此本题我们先尝试暴力 DP。

观察性质，不难发现一个三元组只可能有下面两种形态：

如果要归纳到一种情况，那么可以转化为：中心点 \(x\) 下面挂着两个和 \(x\) 距离都为 \(dis\) 的点，且 \(x\) 的祖先（包含 \(x\) 自己）与 \(x\) 距离为 \(i\)，该祖先的距离与 \(c\) 的距离为 \(dis - i\)。

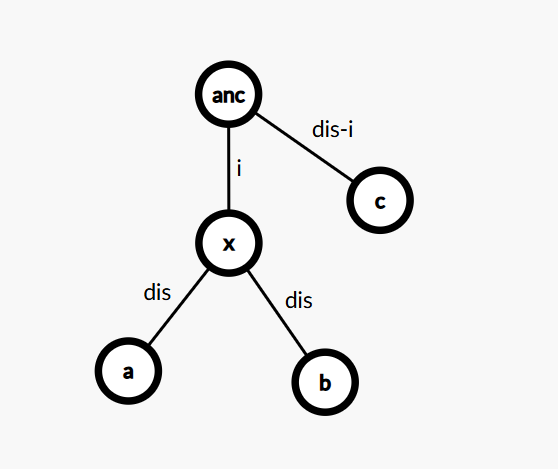
于是可以设计 DP：\(g_{u, d}\) 表示在 \(u\) 子树内，中心点 \(x\) 已经挂了两个到 \(x\) 距离相等的点，要把 \(c\) 加入三元组还需要 \(d\) 的距离的方案数。不难发现上图中的 \(dis-i = d\)。

考虑如何转移，此时发现对每个点新增方案的时候是不好转移的，因为需要枚举距离同时等于 \(d\) 的方案数。于是可以多定义一个 DP 数组：\(f_{u, d}\) 表示在 \(u\) 子树内，到 \(u\) 的距离为 \(d\) 的方案数。这个转移直接从儿子的 \(d-1\) 继承就好了。具体而言：

\[f_{u, d}\gets \sum_v f_{v, d -1} \]

然后 \(g\) 就可以转移了，需要分两种转移：

• 继承儿子：\(g_{u, d} \gets g_{u, d} + \sum_v g_{v, d + 1}\)。
• 对新的三元组进行统计：\(g_{u, d} \gets g_{u, d} + f_{u, d} \times f_{v, d - 1}\)。

最后来统计 \(ans\)，有两种统计方式：

• 对重儿子内已经形成的计数：\(ans \gets ans + g_{u, 0}\)。不计数轻儿子的原因是轻儿子合并的时候会在下一种情况被计数。
• 对合并子树计数：\(ans\gets g_{u, d + 1} \times f_{v, d} + g_{v, d} \times f_{u, d - 1}\)。

不难发现，\(v\) 的第二维下标总是 \(d\)。这是因为我们要枚举轻儿子的第二维，而如果轻儿子的第二维不全是 \(d\)，转移就会变得很麻烦。例如本来合并子树时的式子是 \(ans\gets g_{u, d} \times f_{v, d -1} + g_{v, d+1} \times f_{u, d}\)，就要把 \(d-1,d+1\) 变成 \(d\)，然后让 \(u\) 的第二维偏移，能大幅削减代码难度。

注意这个三个量的转移顺序是 \(ans,g, f\)，因为这三个量会互相影响，必须保证转移使用的量是合并子树前的量。

注意到重儿子的 \(f\) 由 \(u\) 的下标往后偏移一个得到，轻儿子的 \(g\) 由 \(u\) 的下标往前偏移一个得到，于是可以直接长链剖分优化 DP，时间复杂度 \(O(n)\)。

注意一些关于指针的细节，在本题中 \(g\) 因为是向前偏移，所以访问 \(g_{v, 0}\) 的时候实际会访问到 \(g_{u, -1}\)，如果不对此特殊处理的话就会因为访问到其他地方的内存而 WA 掉。有两种处理方式：

• 把 \(f,g\) 都开两倍空间，此时 \(g\) 越界的话会越界到 \(f\) 多开的空间里，这一部分没有使用且是安全的，所以能 AC。

• 只把 \(g\) 开两倍空间，但是 \(g\) 需要指向 p + len[v]，这样访问负数下标的时候就会访问到 \(g\) 已经显式分配的空间里，是安全的。

  这种写法的代码如下：

  f[v] = p; p += len[v];
  g[v] = p + len[v]; p += len[v] * 2;
  

  有一种常见的错误写法：

  f[v] = p; p += len[v];
  p += len[v];
  g[v] = p; p += len[v];
  

  这种写法看似与上文无异，都为负数下标预留了一倍空间。但实际上下面这种写法系统会自动将第二行开辟的空间看做未显式分配的空间，如果直接访问了，系统会为了防止内存泄漏而返回 RE 或者段错误。只有采取第一种写法系统才会把它认为是被显式分配了的空间。

#include <bits/stdc++.h>
#define fi first
#define se second
#define eb(x) emplace_back(x)
#define pb(x) push_back(x)
#define lc(x) (tr[x].ls)
#define rc(x) (tr[x].rs)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ldb;
using pi=pair<int,int>;
const int N = 100005;
int n, len[N], son[N];
int h[N], idx;
ll buf[3 * N], *p = buf, *f[N], *g[N], ans;
struct Edge{
    int v, ne;
}e[2 * N];
void add(int u, int v)
{
    e[++idx] = {v, h[u]};
    h[u] = idx;
}
void dfs1(int u, int fa)
{
    for(int i = h[u]; i ; i = e[i].ne)
    {
        int v = e[i].v;
        if(v == fa) continue;
        dfs1(v, u);
        if(len[son[u]] < len[v]) son[u] = v;
    }
    len[u] = len[son[u]] + 1;
}
void dfs2(int u, int fa)
{
    if(son[u])
    {
        f[son[u]] = f[u] + 1;
        g[son[u]] = g[u] - 1;
        dfs2(son[u], u);
    }
    f[u][0] = 1; ans += g[u][0];
    for(int i = h[u]; i ; i = e[i].ne)
    {
        int v = e[i].v;
        if(v == fa || v == son[u]) continue;
        f[v] = p; p += len[v];
        g[v] = p + len[v]; p += len[v] * 2;
        dfs2(v, u);
        for(int j = 0; j < len[v]; j++)
        {
            ans += g[u][j + 1] * f[v][j];
            if(j > 0) ans += g[v][j] * f[u][j - 1];
        }
        for(int j = 0; j < len[v]; j++)
        {
            if(j > 0) g[u][j - 1] += g[v][j];
            g[u][j + 1] += f[u][j + 1] * f[v][j];
        }
        for(int j = 0; j < len[v]; j++)
        {
            f[u][j + 1] += f[v][j];
        }  
    }
}
int main()
{
    //freopen("sample.in","r",stdin);
    //freopen("sample.out","w",stdout);
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n;
    for(int i = 1; i < n; i++)
    {
        int u, v;
        cin >> u >> v;
        add(u, v);
        add(v, u);
    }
    dfs1(1, 0);
    f[1] = p; p += len[1];
    g[1] = p + len[1]; p += len[1] * 2;
    dfs2(1, 0);
    cout << ans;
    return 0;
}