Luogu P2416 泡芙 题解 [ 蓝 ] [ 边双连通分量 ] [ LCA ]

泡芙：边双连通分量的经典结论题。

总结一下，连通分量有以下常用结论：

• 边双连通分量
  • 同一边双连通分量中，对于任意三个互不相同的点 \(a, b, c\)，必定存在一条不经过重复边的路径，按顺序经过了 \(a, b, c\) 三个点，即路径为 \(a \to b \to c\)。
  • 同一边双连通分量中，对于任意两个不相同的点 \(a, b\) 和一条边 \(e\)，必定存在一条不经过重复边的路径，按顺序经过了 \(a, e, b\) 三个点或边，即路径为 \(a \to e \to b\)。
  • 边双连通分量缩点后的形态是一棵树。
  • 同一边双连通分量中，对于任意两个不同的点 \(a,b\)，他们之间不经过重复边的路径的并集，恰好完全等于这个边双连通分量。
• 点双连通分量
  • 同一点双连通分量中，对于任意三个互不相同的点 \(a, b, c\)，必定存在一条不经过重复点的路径，按顺序经过了 \(a, b, c\) 三个点，即路径为 \(a \to b \to c\)。
  • 同一点双连通分量中，对于任意两个不相同的点 \(a, b\) 和一条边 \(e\)，必定存在一条不经过重复点的路径，按顺序经过了 \(a, e, b\) 三个点或边，即路径为 \(a \to e \to b\)。
  • 每个点双连通分量可以用一个方点代替，原图中的节点用圆点代替，可以利用圆方树解题。
  • 一个点可能属于多个点双连通分量，此时这个点在圆方树上时是非叶子节点。
  • 同一点双连通分量中，对于任意两个不同的点 \(a,b\)，他们之间不经过重复点的路径的并集，恰好完全等于这个点双连通分量。
  • 点双连通分量的定义是不含割点的极大连通分量，边双连通分量的定义是不含割边的极大连通分量。因此点双连通分量一般一定是边双连通分量，点双的限制一般是更强的。但是需要注意两点连边的特殊情况，此时是边双连通分量不是点双连通分量，做点双题目的时候一定要特殊考虑一下这种情况。上述结论同样也是不考虑两点连边这种特殊情况的。

下面对部分结论进行证明：

• 边双连通分量的结论 \(1\)
  • 
  • 考虑这张图，根据边双的定义，\(a,b\) 之间一定存在至少两条不交的路径。于是可以先走与 \(c\) 的连接点（即点 \(1\)）不交的一条路径 \(a\to 4 \to 3 \to b\)，然后再走与 \(c\) 的连接点相交的路径 \(b\to 2 \to 1 \to 5 \to c\) 即可。若 \(1\) 与 \(a\) 重合也是成立的，因为只需要保证不经过重复边即可。
• 边双连通分量的结论 \(2\)
  • 
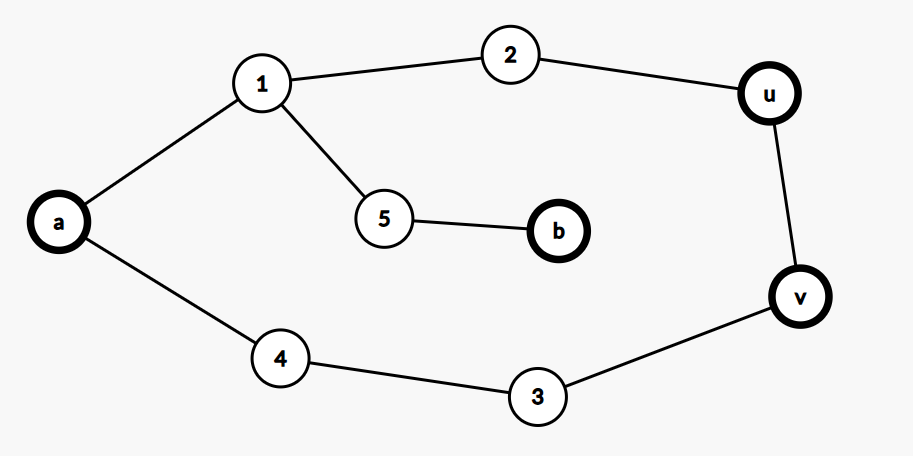
  • 考虑这张图，利用一个经典技巧：边转点。在边 \(e\) 的两端点 \(u, v\) 之间新建一个叫 \(c\) 的点。
  • 
  • 不难发现加了这样一个点后该图依然是边双，于是问题转化为证明存在一条不经过重复边的经过 \(a \to c \to b\) 的路径。可以直接利用结论 \(1\) 来证明。
• 边双连通分量的结论 \(4\)
  • 考虑枚举每条边，问题转化为证明对于每条边 \(e\)，不经过重复边的路径 \(a\to e \to b\) 都存在。然后运用结论 \(2\) 即可证明。
• 点双连通分量的结论证明和边双几乎一样，此处不再赘述。

对于本题，显然对于一个边双连通分量，只要里面存在一条边是 \(1\)，那么整个边双就能吃到泡芙。而对于缩点形成的树，如果树边上存在一条边是 \(1\)，那么依然能吃到泡芙，因此可以利用树上差分求出任意两点之间点权之和与边权之和，判断有无边权为 \(1\) 的路径即可。

时间复杂度 \(O(n\log n)\)，如果使用 Tarjan 离线求 LCA 可以做到 \(O(n)\)。

#include <bits/stdc++.h>
#define fi first
#define se second
#define eb(x) emplace_back(x)
#define pb(x) push_back(x)
#define lc(x) (tr[x].ls)
#define rc(x) (tr[x].rs)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ldb;
using pi=pair<int,int>;
const int N = 300005, M = 600005;
int n, m, dw[N], ew[N], q;
struct Edge{
    int v, ne, w;
}e[M];
int h[N], idx = 1;
void add(int u, int v, int w)
{
    e[++idx] = {v, h[u], w};
    h[u] = idx;
}
int dfn[N], stk[N], tp, low[N], tot, cnt, edcc[N];
void tarjan(int u, int ineg)
{
    dfn[u] = low[u] = ++tot;
    stk[++tp] = u;
    for(int i = h[u]; i ; i = e[i].ne)
    {
        int v = e[i].v;
        if(dfn[v] == 0)
        {
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
        }
        else if(i ^ ineg ^ 1)
        {
            low[u] = min(low[u], dfn[v]);
        }
    }
    if(dfn[u] == low[u])
    {
        cnt++;
        int x;
        do{
            x = stk[tp--];
            edcc[x] = cnt;
        }while(x != u);
    }
}
vector<pi> g[N];
int fa[N], top[N], sz[N], son[N], dep[N];
void dfs1(int u, int f)
{
    sz[u] = 1, fa[u] = f, dep[u] = dep[f] + 1;
    for(auto eg : g[u])
    {
        int v = eg.fi, w = eg.se;
        if(v == f) continue;
        dw[v] += dw[u];
        ew[v] += ew[u] + w;
        dfs1(v, u);
        sz[u] += sz[v];
        if(sz[son[u]] < sz[v]) son[u] = v;
    }
}
void dfs2(int u, int tp)
{
    top[u] = tp;
    if(son[u] == 0) return;
    dfs2(son[u], tp);
    for(auto eg : g[u])
    {
        int v = eg.fi, w = eg.se;
        if(v == fa[u] || v == son[u]) continue;
        dfs2(v, v);
    }
}
int getlca(int u, int v)
{
    while(top[u] != top[v])
    {
        if(dep[top[u]] < dep[top[v]]) swap(u, v);
        u = fa[top[u]];
    }
    if(dep[u] < dep[v]) swap(u, v);
    return v;
}
int main()
{
    //freopen("sample.in","r",stdin);
    //freopen("sample.out","w",stdout);
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> m;
    for(int i = 1; i <= m; i++)
    {
        int u, v, w;
        cin >> u >> v >> w;
        add(u, v, w);
        add(v, u, w);
    }
    for(int i = 1; i <= n; i++)
        if(dfn[i] == 0)
            tarjan(i, -1);
    for(int i = 2; i <= idx; i += 2)
    {
        int u = e[i].v, v = e[i ^ 1].v, w = e[i].w;
        if(edcc[u] == edcc[v])
        {
            if(w == 1)
                dw[edcc[u]] = 1;
        }
        else
        {
            g[edcc[u]].push_back({edcc[v], w});
            g[edcc[v]].push_back({edcc[u], w});
        }
    }
    dfs1(1, 0);
    dfs2(1, 1);
    cin >> q;
    while(q--)
    {
        int u, v;
        cin >> u >> v;
        u = edcc[u], v = edcc[v];
        int lca = getlca(u, v);
        int res = ew[u] + ew[v] - 2 * ew[lca] + dw[u] + dw[v] - dw[lca] - dw[fa[lca]];
        if(res > 0) cout << "YES\n";
        else cout << "NO\n";
    }
    return 0;
}