Luogu P4249 WC2007 剪刀石头布 / Codeforces 1264E Beautiful League 题解 [ 黑 ] [ 费用流建模 ] [ 竞赛图 ] [ 差分 ]

剪刀石头布：有点牛的竞赛图费用流。

观察

首先发现这个图是一张竞赛图，也就是把有向边看作无向边时是完全图。

我们先不考虑最大化三元环个数，先考虑如何计算这个东西。

正着做显然不太好做，没办法在一个很短的时间内用一个式子表达出来。于是我们先考虑观察三元环的形态。

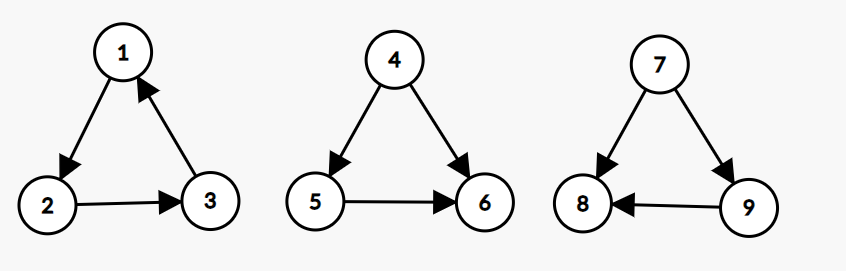
容易发现第一个可以形成三元环，后两个不能形成三元环。

那么第一个和后两个之间的区别是什么呢？可以发现三元环上所有点的出度为 \(1\)，而非三元环所有点的出度分别是 \(0,1,2\)。

非三元环的特征就是出现 \(0,2\) 为出度的点，出度为 \(0\) 肯定是不太好统计的，所以考虑根据出度为 \(2\) 来统计。假设某个点的出度是 \(c_i\)，那么以 \(i\) 为出度 \(2\) 的环的个数就是 \(C_{c_i}^2\)。因为随便挑两个无向边定向出去就能形成非三元环了。总非三元环个数为 \(\sum_{i=1}^n C_{c_i}^2\)。

于是一个正难则反的思路就出来了。因为这个图是一个竞赛图，所以我们随便选三个点就能使得他们之间有边，则总环个数为 \(C_{n}^3\)。只要我们算出非三元环个数，拿总数减掉它就可以算出三元环个数了。

因此，我们可以把原问题转化为：给无向边定向，使得 \(\sum_{i=1}^n C_{c_i}^2\) 的值最小。

建模

不难想到把每条无向边 \((u,v)\) 看作一个节点 \(x\)，然后连边 \((S,x,1,0)\)。后两个数分别指边的容量和费用。接下来连边 \((x,u,1,0)\) 和 \((x,v,1,0)\)。表示定向二选一。

在已经确定了所有边的定向后，如何在费用流上表示出原式子呢？因为不同度数的费用是不同的，所以考虑利用差分拆每增加一个度数的贡献，然后进行拆边。

差分的结果是 \(C_i^2-C_{i-1}^2=i-1\)，把 \((u,T,1,i-1)\) 加入图中即可。其中 \(1 \le i \le n+1\)，同时因为求的是最小代价，费用流会自动先选费用低的边流，所以这个建图方式是可以接受的。

跑最小费用最大流即可，时间复杂度就是 EK 或者 Dinic 的复杂度。

代码

#include <bits/stdc++.h>
#define fi first
#define se second
#define eb(x) emplace_back(x)
#define pb(x) push_back(x)
#define lc(x) (tr[x].ls)
#define rc(x) (tr[x].rs)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ldb;
using pi=pair<int,int>;
const int N=100005,M=5000005,K=105;
const ll inf=0x3f3f3f3f3f3f3f3f;
int n,m,a[K][K],s,t,id[K][K][2];
int h[N],cur[N],idx=1;
struct Edge{
    int v,ne;
    ll c,w;
}e[M];
void add(int u,int v,ll c,ll w)
{
    e[++idx]={v,h[u],c,w};
    h[u]=idx;
}
void addeg(int u,int v,ll c,ll w)
{
    add(u,v,c,w);
    add(v,u,0,-w);
}
int getid(int x,int y)
{
    return ((x-1)*n+y);
}
ll d[N],cost;
bitset<N>vis;
bool SPFA()
{
    memset(d,0x3f,sizeof(d));
    vis.reset();
    queue<int>q;
    q.push(s);
    vis[s]=1;
    d[s]=0;
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        vis[u]=0;
        for(int i=h[u];i;i=e[i].ne)
        {
            int v=e[i].v;ll c=e[i].c,w=e[i].w;
            if(d[v]>d[u]+w&&c)
            {
                d[v]=d[u]+w;
                if(vis[v]==0)
                {
                    vis[v]=1;
                    q.push(v);
                }
            }
        }
    }
    return (d[t]<=inf/2);
}
ll dfs(int u,ll mf)
{
    if(u==t)return mf;
    ll sm=0;
    vis[u]=1;
    for(int i=cur[u];i;i=e[i].ne)
    {
        int v=e[i].v;ll c=e[i].c,w=e[i].w;
        cur[u]=i;
        if(vis[v]==0&&d[v]==d[u]+w&&c)
        {
            ll res=dfs(v,min(mf,c));
            cost+=w*res;
            e[i].c-=res;
            e[i^1].c+=res;
            mf-=res;
            sm+=res;
            if(mf==0)break;
        }
    }
    if(sm==0)d[u]=inf;
    return sm;
}
ll dinic()
{
    ll flow=0;
    while(SPFA())
    {
        memcpy(cur,h,sizeof(h));
        vis.reset();
        flow+=dfs(s,inf);
    }
    return flow;
}
int main()
{
    //freopen("sample.in","r",stdin);
    //freopen("sample.out","w",stdout);
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin>>n>>m;
    s=n*n+n+1,t=n*n+n+2;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(i!=j)a[i][j]=2;
        }
    }
    while(m--)
    {
        int u,v;
        cin>>u>>v;
        a[u][v]=1;
        a[v][u]=0;
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(a[i][j]==1)
            {
                addeg(s,getid(n+1,i),1,0);
            }
            else if(a[i][j]==2&&i<=j)
            {
                addeg(s,getid(i,j),1,0);
                addeg(getid(i,j),getid(n+1,i),1,0);
                id[i][j][0]=idx;
                id[j][i][1]=idx;
                addeg(getid(i,j),getid(n+1,j),1,0);
                id[i][j][1]=idx;
                id[j][i][0]=idx;
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=n;j++)
        {
            addeg(getid(n+1,i),t,1,j);
        }
    }
    dinic();
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(i==j)cout<<0;
            else if(a[i][j]<2)cout<<a[i][j];
            else cout<<(e[id[i][j][0]].c==1);
        }
        cout<<endl;
    }
    return 0;
}

总结

这题其实就是观察到答案如何用式子表示出来，然后根据推出的数学式子进行建模。还是挺常规的。