人工智能之机器学习线代基础——行列式的性质和法则

行列式是一种重要的代数工具，用于描述方阵的一些核心特性，如矩阵是否可逆、线性相关性等。为了快速准确地计算行列式，我们可以利用行列式的性质和法则，包括对消法则、行列变换等。

 

1. 行列式的基本性质

1.1 交换行（列）会改变符号

如果将行列式的两行或两列进行交换，则行列式的符号会变为相反数：

 

1.2 如果某行（列）是零，则行列式为零

如果行列式中有一整行或整列元素为零，那么行列式值为零：

 

1.3 行（列）的线性组合不改变行列式

对某行（列）进行线性变换，即将其加上其他行（列）的倍数，不会改变行列式的值。

例如：

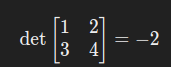
 将第 2 行替换为 “第 2 行 - 3 倍第 1 行”：

 

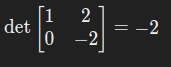
1.4 行列倍乘性

如果将某行（列）中的所有元素都乘以一个常数 kkk，那么行列式值也会乘以 k：

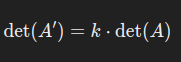
 例如：

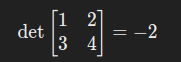
将第一行乘以 2：

 

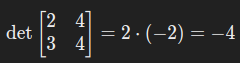
1.5 行列相关时，行列式为零

如果矩阵的两行（列）线性相关，则行列式为零： 

 

2. 行列式的计算法则

2.1 对 2×2 矩阵

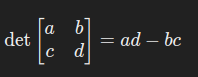
例如：

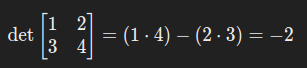
2.2 对 3×3 矩阵：按行展开法 

对于矩阵：

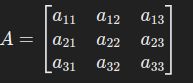
 按第一行展开：

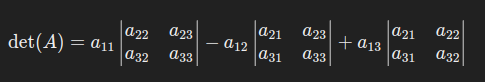
人工智能之机器学习线代基础——证明 行列式的递归展开公式（通常称为 Laplace 展开）的成立

2.3 对高阶矩阵：化简法（对消与初等变换）

通过对行列式的行（列）进行变换，可以简化计算。

步骤

1. 选主元：选择某行或某列，优先选择包含较多零元素的行或列。
2. 初等变换：通过加减行（列），将矩阵化为上三角或对角矩阵。
3. 计算行列式：上三角矩阵的行列式为对角线元素的乘积。

示例

计算：

 

(1) 初等变换：消除第 1 列的非零元素

• 第 2 行减去 2 倍第 1 行：

  

• 第 3 行减去 3 倍第 1 行： 

  

(2) 再次消除第 2 列的非零元素

• 第 3 行减去 9 倍第 2 行：

  

   

(3) 计算行列式 上三角矩阵的行列式为对角线元素的乘积：

det⁡=2⋅1⋅(−7)=−14

3. 行列式的应用

3.1 判断矩阵是否可逆

矩阵 A可逆当且仅当 det⁡(A)≠0。

3.2 解线性方程组

克拉默法则通过行列式求解线性方程组。

3.3 计算体积

行列式可以用于计算向量构成的平行多面体的体积。

4. 总结

操作	影响
交换行或列	改变符号：det⁡=−det
某行或列全为零	det⁡=0
线性相关行或列	det⁡=0
对某行加减其他行倍数	det不变
某行或列乘以常数 kkk	det⁡=k⋅det⁡
上三角矩阵或对角矩阵	对角线元素的乘积

行列式的计算依赖性质和变换，通过化简法可以快速处理高阶矩阵。