矩阵正定、负定、半正定、半负定

矩阵正定

对于实对称矩阵正定《==等价条件==》非任意零实系数向量z，>0

对于埃尔米特矩阵（复数共轭对称矩阵）正定《==等价条件==》于任意非零复数向量z，

==等价条件==

1. 矩阵的所有特征值都是正的；
2. 顺序主子式大于零
3. 对任意非零向量x, x’Ax > 0.

矩阵负定、半定、不定

为埃尔米特阵，表示向量z的共轭转置

==负定==

对于矩阵,对于所有非零向量z， ;

一、负定矩阵判别方法有：
1、 A 的特征值都小于0
2、A的k阶顺序主子式 * (-1)^k > 0
3.、对任意非零向量x, x’Ax < 0.

（也就是偶数阶主子式为正，奇数阶主子式为负）。
顺序主子式是行列式，第k阶顺序主子式就是矩阵的前k行和前k列组成的行列式，

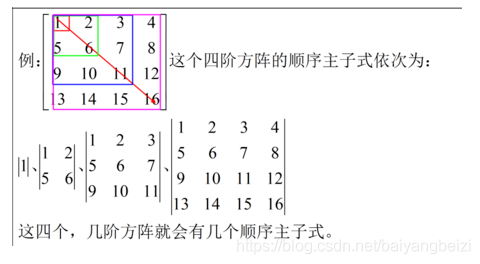
==半正定==

对于所有非零向量z， ;

==半负定==

对于所有非零向量z， ;

==不定==

既不半正定也不半负定

conclusion

1. 正定负定是相对于对称矩阵、埃尔米特阵来说的；