费用流做题记录(二)
链接
P4694 [PA 2013] Raper - 洛谷 | 计算机科学教育新生态
Buy Low Sell High - 洛谷 | 计算机科学教育新生态
Olympiad in Programming and Sports - 洛谷 | 计算机科学教育新生态
【UER #8】雪灾与外卖 - 题目 - Universal Online Judge
P6122 [NEERC 2016] Mole Tunnels - 洛谷 | 计算机科学教育新生态
P3826 [NOI2017] 蔬菜 - 洛谷 | 计算机科学教育新生态
P5470 [NOI2019] 序列 - 洛谷 | 计算机科学教育新生态
#574. 「LibreOJ NOI Round #2」黄金矿工 - 题目 - LibreOJ
#6405. 「ICPC World Finals 2018」征服世界 - 题目 - LibreOJ
Raper
本题有两种做法
- 双 \(\log\) 的 wqs 二分 + 反悔贪心。
- 单 \(\log\) 的模拟费用流。
无论如何,费用流建模是必须的。
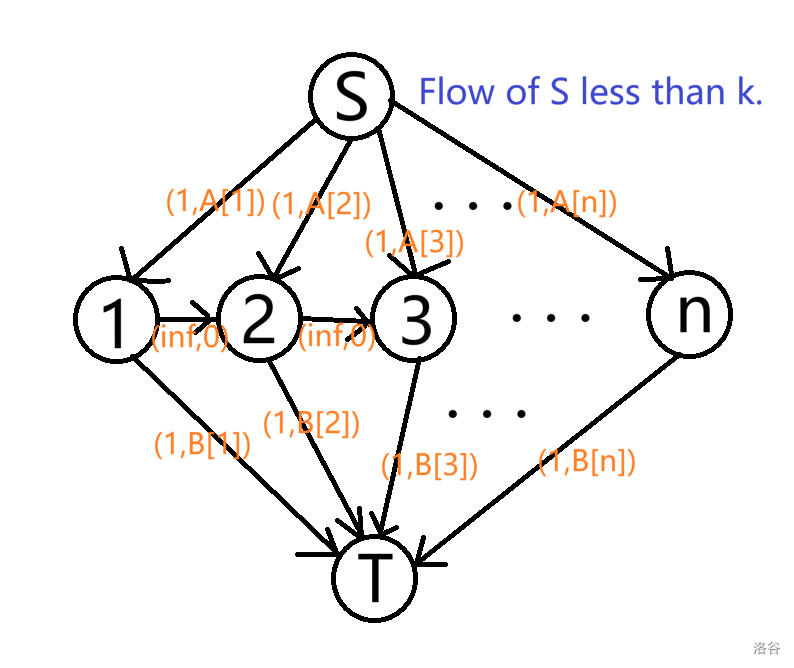
反悔贪心做法:由于本题可以转化为费用流模型,所以不妨设答案为 \(f(k)\),\(k\) 在图中为源点流出流量,则 \(f\) 具有凸性,于是就可以使用 wqs 二分去除 \(k\) 这一限制。
无 \(k\) 这一限制后,就可以反悔贪心了。具体来讲,遍历 \(i\in (1,2,\dots,n)\),同时考虑图中 \(A_i\) 和 \(B_i\) 相关的边。模拟的费用流算法为:增量 - 轴枢。
时间复杂度 \(O(n\log n\log V)\)
模拟 SSP 做法:建图后,在 SSP 算法下,增广路不会有圈,又由于图的形态,费用关于源点和汇点的边不会退流,所以就可以用线段树维护最短路。
因为流动原因,线段树需要维护区间加和区间减操作,所以线段树节点要维护残量最小值、
比区间最小值更大的流动区间等信息。
时间复杂度 \(O(n+k\log n)\)。该算法还可以以同样的复杂度求出 \(k\) 取遍 \((1,2,\dots,n)\) 的答案。
wqs 二分
往往能直接去除个数限制,并给复杂度添加一个 \(\log\)。
费用流与凸性
由于 SSP 算法的正确性,费用流的源点流量限制与最小费用形成凸包。这可能可以和很多凸相关算法结合使用。
这也常用于证明某函数的凸性。
可能的结合:
- wqs 二分。
- 决策单调性优化。
二分的实现
在离散的二分中,通常使用左闭右开或左开右闭的实现方法。下面是伪代码。
- 注:使用 \(P(x)\) 代表关于整数 \(x\) 的命题。
\([l,r)\) 版本:
- function \(\text{search}(l,r)\)
- while \(l<r\) do
- let \(\displaystyle \text{mid}\gets\lfloor\frac{l+r}{2}\rfloor\)
- if \([P(x)]=0\) then
- \(l\gets\text{mid}+1\)
- else
- \(r\gets \text{mid}\)
- return \(l\)
- while \(l<r\) do
\((l,r]\) 版本:
- function \(\text{search}(l,r)\)
- while \(l<r\) do
- let \(\displaystyle \text{mid}\gets\lfloor\frac{l+r+1}{2}\rfloor\)
- if \([P(x)]=0\) then
- \(l\gets\text{mid}\)
- else
- \(r\gets \text{mid}-1\)
- return \(r\)
- while \(l<r\) do
轴枢与增广路
这是关于费用流算法的比较。
轴枢:在图中寻找负圈,并将其推流。这一过程保持源点流出量不变。
增广路:在图中寻找源汇点之间的最短路,并将其推流。这一过程将增加源点流出量,并且不会形成圈。
它们的性质可以在很多费用流问题中产生作用。
可以将轴枢对应为为反悔贪心,而增广路则是简单的取最短路。
强信息反而易于维护
通常被认为是线段树技巧。可能也用于分块、平衡树等。
下面的信息可能好维护:
- 环上的和或乘积。
- 最小值等排名相关信息。
- 历史信息。
可能还要更多。
Buy Low Sell High
反悔贪心题。
Submission #302970552 - Codeforces
也可以建费用流。
种树
居然可以费用流建模?
有经典的贪心做法和 wqs 二分做法。
可以使用费用流建模快速证明其正确性。
不妨设获利数组为 \(C\),则可如下图建模。(答案为流量为 \(k\) 的最小费用)似乎这种方法没什么可拓展性。
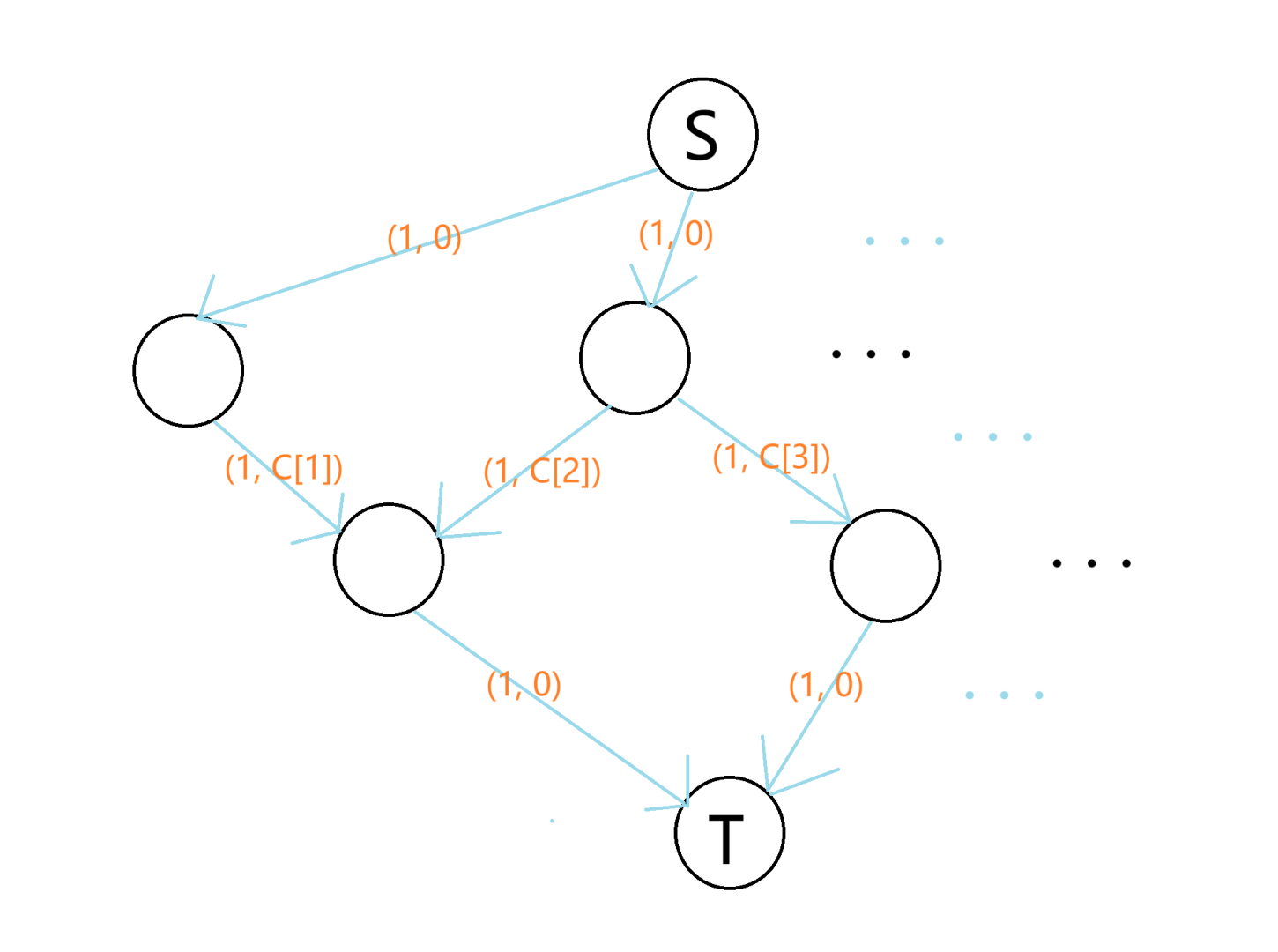
代码懒得写了。
Olympiad in Programming and Sports
简单贪心题。
Submission #303489962 - Codeforces
Olympiad in Programming and Sports - 洛谷
容易建出二分图(费用流建模)。
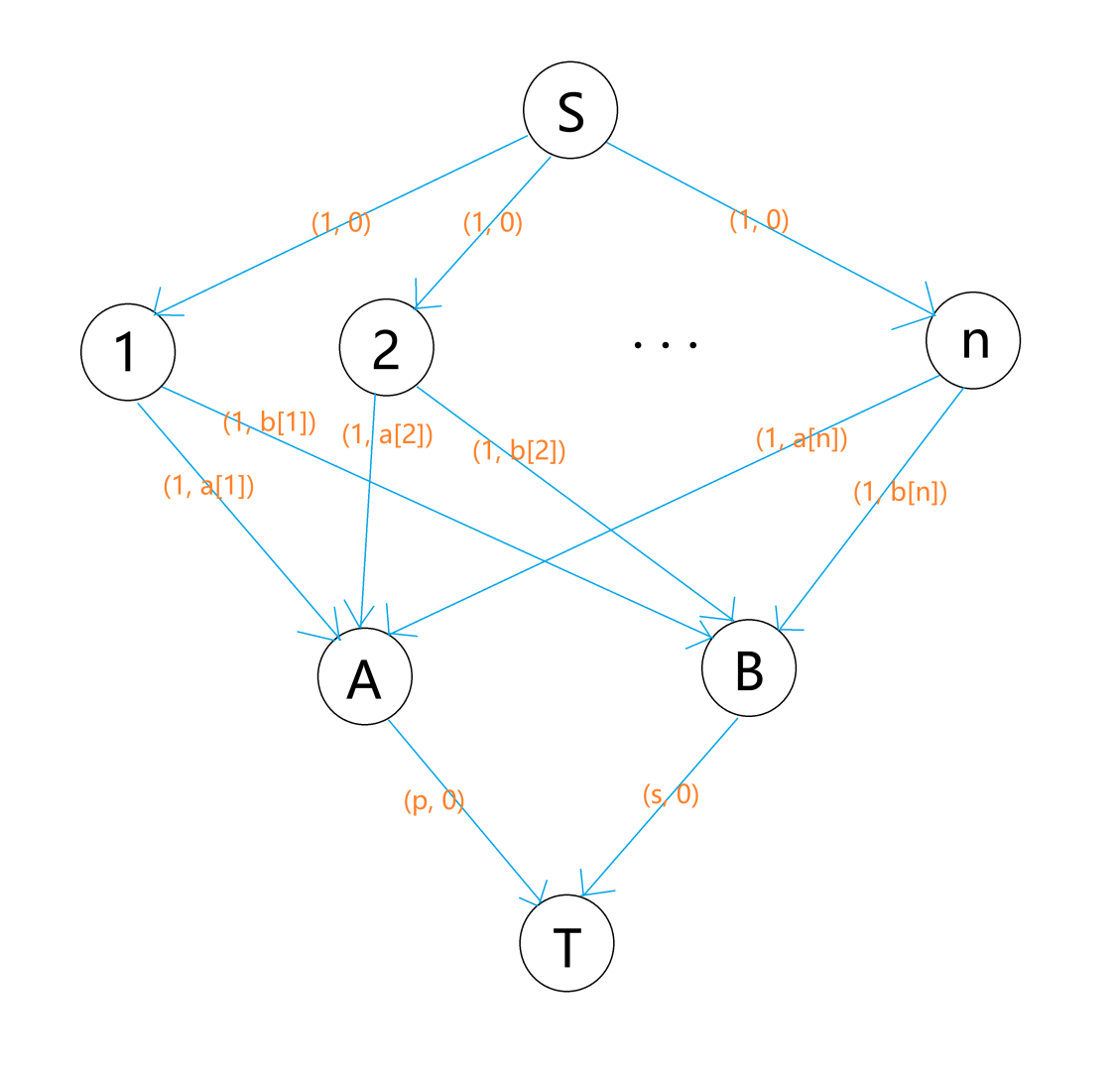
直接用几个可删堆模拟一下 SSP 即可。
时间复杂度 \(O(n\log n)\)。
Mole Tunnels
P6122 [NEERC 2016] Mole Tunnels - 洛谷
直接增量费用流模型即可。能够做到 \(O(n\log n)\)。
增量费用流模型
性质很强。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号