网络流笔记

模拟费用流小记 - 洛谷专栏

网络流/二分图相关笔记(干货篇) - 洛谷专栏

链接

各种写法的网络流 记录详情 - 洛谷

网络流库 记录详情 - 洛谷

网络流库 - zhiyin123123 - 博客园

SPFA + EK 记录详情 - 洛谷

做题记录

费用流做题记录（一） - zhiyin123123 - 博客园

约定

• 如无特殊说明，\(n\) 为图的点数，\(m\) 为图的边数，\(s\) 为源点，\(t\) 为汇点。
• 对于节点 \(u,v\)，\(\operatorname{dis}(u,v)\) 表示 \(u\) 到 \(v\) 的最短路长度。

最大流

Ford–Fulkerson 方法

设最大流为 \(f\)，单轮增广复杂度为 \(\mathcal{T}(n,m)\)，则该方法复杂度为

\[O(f\times T(n,m)) \]

说明：因为每轮增广至少会让当前流增加 \(1\)。

EK 算法

每次使用最短路进行增广，找最短路复杂度为 \(O(m)\)（bfs），增广轮数可以被证明为 \(O(nm)\)，所以时间复杂度为

\[O(nm^2) \]

最短路不减

\(\forall\) 节点 \(u\)，设其经过一次增广后，\(s\) 到 \(u\) 的距离变为 \(\operatorname{dis}'(s,u)\)，则有

\[\operatorname{dis}(s,u)\leq \operatorname{dis}'(s,u) \]

证明可以随便画个图分讨一下。

EK 增广轮数证明

每次增广至少有一条边流满。

对于每条边（不妨设其为 \(1\to 2\)），某次将要对它增广流满时距离为 \(\operatorname{dis}\)，下一次将对它（的反边）增广流满时距离为 \(\operatorname{dis}'\)，则不妨设

\[\begin{gathered} d_1=\operatorname{dis}(s,1)\\ d_2=\operatorname{dis}(s,2)\\ d_1'=\operatorname{dis}'(s,1)\\ d_2'=\operatorname{dis}'(s,2) \end{gathered} \]

根据满流后边会反向，由于增广路的最短性，得到

\[\begin{gathered} d_2=d_1+1\\ d_1'=d_2'+1 \end{gathered} \]

所以可得

\[d_1+1=d_2\leq d_2'=d_1'-1 \]

所以有

\[d_1<d_1' \]

节点 \(1\) 的距离时单增的。由于最远距离是 \(n\)，所以增广轮数为

\[O(nm) \]

Dinic 算法

建分层图再增广，建分层图复杂度 \(O(m)\)，分层图建 \(O(n)\) 轮（层数最多为 \(n\)），每个分层图增广复杂度 \(O(nm)\)，总复杂度 \(O(n(m+mn))\)，即

\[O(n^2m) \]

特殊图的复杂度分析

在边容量相等的图中，每个分层图增广的复杂度为

\[\boxed{O(m)} \]

证明：每条边只会被遍历一次。遍历一次就流满了。

---

在容量相等的图中，建立分层图的次数为

\[\boxed{O(\sqrt m)} \]

证明：进行 \(\sqrt m\) 轮分层图建立后，分层图层数至少为 \(\sqrt m\)。对于分层图 \(G\)，设其第 \(i\) 层的点集为 \(V_i\)，我们称边 \(a\to b\) 属于其第 \(i\) 层，当且仅当 \(a\in V_i,b\in V_{i+1}\)。则此时分层图中至少存在一个层满足其包含的边数不超过 \(\displaystyle \frac{m}{\sqrt m}=\sqrt m\)，这使得之后的最大流与当前流之差超过 \(\sqrt m\)，所以只能再增广 \(\sqrt m\) 轮。

---

在容量相等的图中，建立分层图的次数为

\[\boxed{O(n^{\frac{2}{3}})} \]

证明：与上面哪个类似。进行 \(n^{\frac{2}{3}}\) 轮分层后，至少有一层 \(i\) 满足 \(\displaystyle |V_i|\times|V_{i+1}|\leq \left(\frac{n}{n^{\frac{2}{3}}}\right)^2=n^{\frac{2}{3}}\)。后面类似。

---

在容量相等的图中，Dinic 复杂度为

\[\boxed{O(m\sqrt m),O(mn^{\frac{2}{3}})} \]

---

二分图匹配中，Dinic 复杂度为

\[\boxed{O(m\sqrt n)} \]

说明：因为二分图中一个节点要么入度为 \(1\)，要么出度为 \(1\)，使得一个点只能对应一个的最大流之一。

费用流

SSP 算法

每次找一条最短路进行增广。正确性基于没有负环。

基于 SPFA

使用 SPFA + EK 时，通常不会被卡。

原始对偶

慢。

为了让边权变成正的，通常的做法时给每个点赋予一个势能，给点 \(v\) 赋予势能 \(h(v)\)，并定义 \(h(v)\) 为 \(v\) 到某定点的距离，然后，对于边 \(u\to v\)，设其边权为 \(w\)，则将边权变为 \(w+h(u)-h(v)\)，由于三角形不等式，它是正的，求出 \(s\) 到 \(v\) 的最短路后将答案加上 \(-h(s)+h(t)\) 即可。

进行增广后，可能会产生一些新的边，若某新增边的反边在改造后的图中权值为 \(w'\)，则容易发现，这条新增边的权值恰好为 \(-w'\)。不妨设该新增边为 \(v\to u\)，则可设产生新边前 \(d_v\) 为源点到 \(v\) 的距离，则可令所有点的势能增加 \(d_v\)，于是 \(-w'\) 变为 \(-w'+d_v-d_u\)，由于增广路的最短性，有：

\[d_v=w'+d_u \]

所以 \(-w'+d_v-d_u=0\)，非负了。其他边容易验证同样非负。

实际上，这种点上用距离做势能是很常见的技巧，在网络单纯形算法中也有出现。

实际上，这个做法的本质是图上差分。

网络单纯形

网络单纯形算法学习笔记 - zhiyin123123 - 博客园

SSP 算法的正确性

假设最小费用最大流初始无负环，并且经过 \(k\) 轮增广后残量图仍无负环，现证第 \(k + 1\) 轮增广后残量图中也无负环。

设增广前的图为 \(G\)，假如增广后产生负环，那么增广路中某条边产生的虚拟反边，一定是该负环的必要组成部分。

如下图所示，

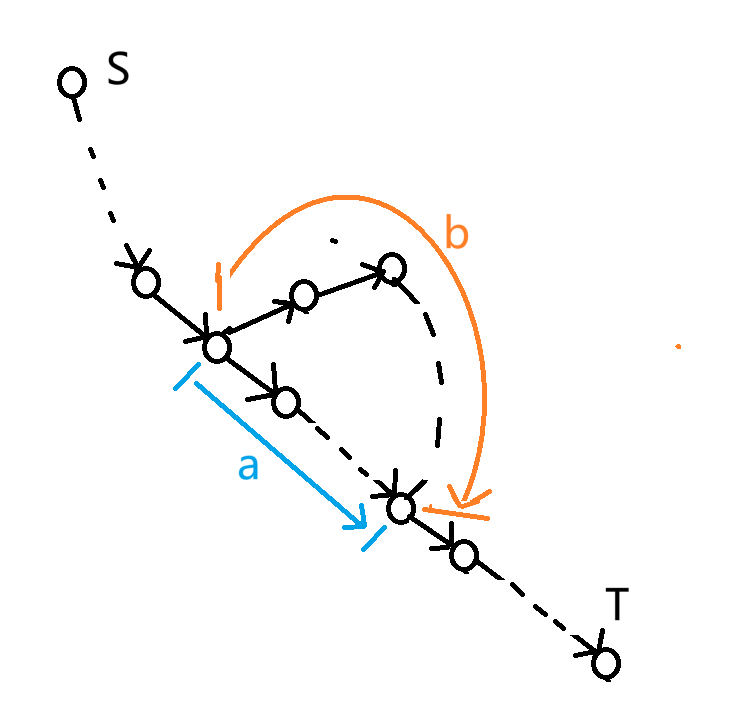
若增广路经过了 \(a\) 段，那么，由于其最短性，有（\(a\) 也代表 \(a\) 段的所有边费用之和，\(b\) 同理）

\[a\leq b \]

假设 \(a\) 的反边和 \(b\) 产生了负环，那么有

\[-a + b < 0 \]

矛盾！

证毕。

增量最小费用任意流模型

首先，对于最小费用任意流模型，可以给源点连出的边增加费用 \(-\inf\)，就可以转化为最小费用最大流问题了。当然，也可以使用网络单纯性的方法。

对于一个最小费用最大流的残量图 \(G\)，为其添加一条容量为 \(1\) 的边（费用任意）得到图 \(G'\)，则仅可能出现三种情况：

1. 权值最小的增广路是负环，则沿着它增广后，得到最优解。
2. 权值最小的增广路是负权简单路，则沿着它增广后，得到最优解。
3. 权值最小的增广路是正的，该图本身就是最优解。

情况 2 和 3 正确性显然，情况 1 可以与 SSP 算法正确性证明类似。