费用流做题记录(一)
P4016 负载平衡问题 - 洛谷 | 计算机科学教育新生态
P4452 [国家集训队] 航班安排 - 洛谷 | 计算机科学教育新生态
P2045 方格取数加强版 - 洛谷 | 计算机科学教育新生态
P2050 [NOI2012] 美食节 - 洛谷 | 计算机科学教育新生态
P2053 [SCOI2007] 修车 - 洛谷 | 计算机科学教育新生态
P2770 航空路线问题 - 洛谷 | 计算机科学教育新生态
P3159 [CQOI2012] 交换棋子 - 洛谷 | 计算机科学教育新生态
P3356 火星探险问题 - 洛谷 | 计算机科学教育新生态
P3358 最长k可重区间集问题 - 洛谷 | 计算机科学教育新生态
P4013 数字梯形问题 - 洛谷 | 计算机科学教育新生态
P5331 [SNOI2019] 通信 - 洛谷 | 计算机科学教育新生态
网络流库
负载平衡问题
简单贪心或费用流。
贪心做法:
枚举断点进行断环成链,然后在链上贪心。正确性的话,是因为断点一定存在。
容易做到 \(O(n^2)\)。
费用流做法:
首先,算出平均值 \(\overline A\),设源点为 \(S\),汇点为 \(T\),建立点 \(1,2,\dots,n\),然后
- 若 \(A_i>\overline A\),连 \(S\to i\),容量为 \(A_i-\overline A\),费用为 \(0\).
- 若 \(A_i<\overline A\),连 \(i\to T\),容量为 \(\overline A-A_i\),费用为 \(0\).
然后 \(\forall i,j,i+1\equiv j\ (\operatorname{mod} n)\),
- 连 \(i\leftrightarrow j\),容量为 \(\inf\),费用为 \(1\).
然后最大流的最小费用就是答案。
复杂度小常数 \(O(n^3)\)(SPFA + EK).
航班安排
按照时间个给机场建分层图(跑费用流)复杂度错误,但是,分层图中有用的节点个数只有 \(O(M)\) 个,所以可以暴力两两连边,正确性由数据范围的 \(t_{i,j}\leq t_{i,k}+t_{k,j},f_{i,j}\leq f_{i,k}+f_{k,j}\) 保证。
复杂度为 \(O(N^3K)\)。
有些细节没说。
方格取数加强版
直接把走的 \(k\) 次看成 \(k\) 条流即可。
实现时,需要拆点。
复杂度 \(O(kn^5A)\).
美食节
考虑使用厨师匹配菜,尝试使用费用流。
发现,一个初始做的第 \(i\) 道菜代价会 \(\times i\)(拆贡献),所以建立分层图,以厨师编号和已做菜数量建立。每个分层厨师都要和所有菜的节点连边。
直接建图点数 \(\Theta(mp+n)\),边数 \(\Theta((mp+n)n)\),边数太大,费用流跑不动。
于是卡常,进行动态开点,厨师做了菜才会做下一道菜,所以可以每增广一次就判断最后一层厨师是否被经过,如果经过了,就开下一层点。
边数 \(\Omega((n+m+p)n)\),根本卡不掉。
动态开点 or 边
十分强大的卡常技巧。
航空路线问题
这题有🤡【小丑】 dp 做法。
费用流做法:
把一来一回看成从左到右的两条流。然后就很简单了。
复杂度 \(O(nm)\)(\(O(n^3)\))。
dp 做法:(没写)
还是看成从左到右的两条流。
设 \(f[i][j]\) 表示两条流目前分别走到了 \(i,j\) 节点,接下来只能往 \(\max\{i,j\}\) 之后转移。正确性显然。
暴力实现复杂度 \(O(n^3)\)。
交换棋子
负载平衡问题。
需要注意的是,一条流的开头和结尾的交换次数为 \(1\),中间为 \(2\)。
最长 \(k\) 可重区间集问题
如下图所示建图。
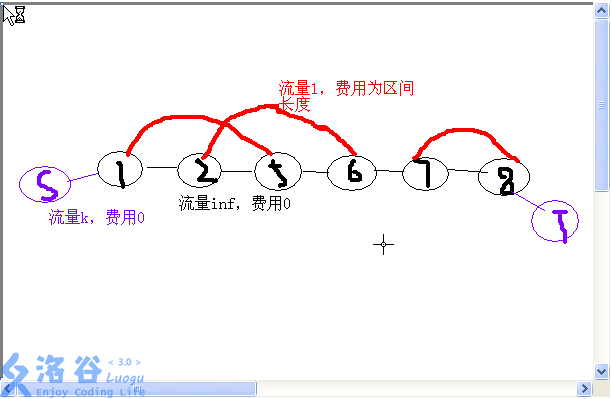
点数 \(O(n)\),边数 \(O(n)\),最大流 \(O(k)\),复杂度 \(O(n^2k)\)(SPFA + EK)。
通信
归并排序优化建图或主席树优化建图。可以使用网络单纯形暴力通过。
首先,把问题转化成最小权链覆盖,具体的,把每个哨站拆成入点和出点,然后前后匹配。
暴力建图边数是 \(O(n^2)\) 的。
对于值域,显然可以建立值域链,不过有前后连边的方向要求。
可以用归并排序优化为 \(O(n\log n)\),使用主席树同样可以。
归并排序的更多应用
本题是二维偏序的建图,但用扫描线要套上主席树,而归并排序就是一种更好些的做法。
此时,归并排序不止能由于三位偏序了。
类似的应用可能是分治 FFT。
网络单纯形
远快于其他费用流算法,好写,但有点长。
跑网络流没有 HLPP 快。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号