拓扑排序

定义

AOV 网：以顶点表示活动，以有向边表示活动之间的优先关系的有向图简称为 AOV 网 。
DAG：结点间通过有向边连接且不存在任何循环的图结构，称为有向无环图，缩写为 DAG。
拓扑序列：在 AOV 网中，若不存在回路（DAG），则所有活动可排列为一个线性序列，使每个活动的前驱活动都排在它之前，称该序列为 拓扑序列 。
拓扑排序：由 AOV 网构造拓扑序列的过程称为 拓扑排序 。

根据定义，拓扑排序仅适用于 DAG。而 DAG“结构上无环，过程上有（拓扑）序”的良好性质，又为处理 DAG 上的 DP 提供了方便。

实现

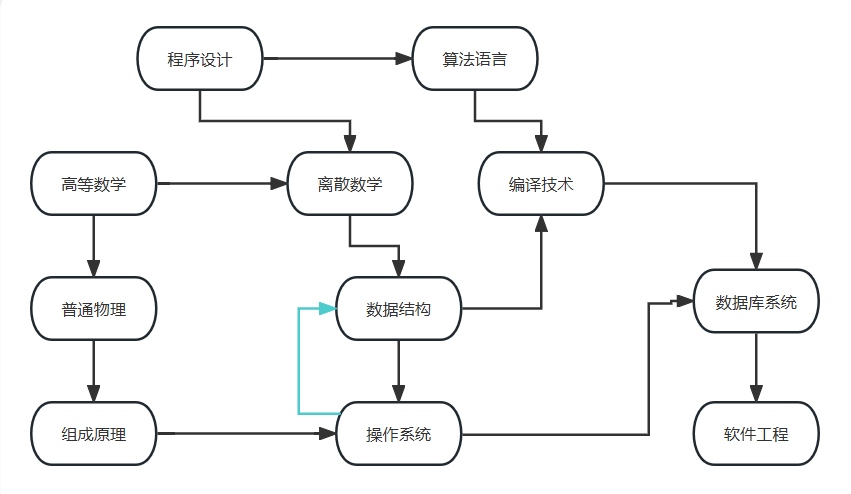
topo-sort-example

以上图计算机专业课部分学习流程图为例，考察拓扑排序的实现方法如下。

初始化队列，将所有入度为 \(0\) 的点入队。
取出队首，遍历其出边，将能够到达的点的入度减 \(1\)，同时维护答案数组。
若此时一个点的入度变为 \(0\)，那么将其入队。
回到第二步，直到队列非空。

注意：如果图中存在环（如“操作系统”的前驱活动是“数据结构”，而“数据结构”的前驱活动又是“操作系统”时），则不存在合法的拓扑序列，此时遍历过的点的数目一定不等于点的总数目。利用这条性质，我们可以判断图中是否有环。

点击查看代码

int in[N], n;
vector<int> e[N], ans;
bool topo() {
    queue<int> q;
    for (int i = 1; i <= n; i++)
        if (in[i] == 0) q.push(i);
    int cnt = 0;
    while (!q.empty()) {
        int u = q.front(); q.pop();
        cnt++;
        for (int v : e[u])
            if (--in[v] == 0) q.push(v);
        ans.push_back(u);
    }
    return cnt == n;
}

例题

朴素拓扑

Pair of Balls

模拟样例并结合“每种颜色恰有 \(2\) 个球”可以发现，将栈顶至栈底两两元素依次连有向边后，跑拓扑排序判环即可。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 8;
int in[N], n, m;
vector<int> e[N];
bool topo() {
    queue<int> q;
    for (int i = 1; i <= n; i++) if (in[i] == 0) q.push(i);
    int cnt = 0;
    while (!q.empty()) {
        int u = q.front(); q.pop(); cnt++;
        for (int v : e[u]) if (--in[v] == 0) q.push(v);
    }
    return cnt == n;
}
int main() {
    cin >> n >> m;
    for (int i = 1, k, lst, cur; i <= m; i++) {
        cin >> k >> lst; k--;
        while (k--) {
            cin >> cur;
            e[lst].push_back(cur);
            in[cur]++;
            lst = cur;
        }
    }
    cout << (topo() ? "Yes" : "No");
    return 0;
}

Milking Order

发现 \(X\) 具有单调性，考虑用二分答案维护 \(X\) 的最大值。对于前 \(mid\) 组约束条件重新建图后，跑朴素的拓扑排序判断 \(mid\) 是否可行。确定 \(X\) 的最大值后，因为要求字典序最小的拓扑序列，可以用小根堆维护拓扑排序的过程。时间复杂度为 \(O(n \log n)\)。

注意：二分 check 函数不需要用小根堆，否则复杂度将变为 \(O(n \log ^ 2 n)\)。对于本题 n 为 \(10^5\) 规模的数据部分点会 TLE。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 8;
int in[N], n, m;
vector<int> e[N], c[N], ans;
void build(int mid) {
    for (int i = 1; i <= n; i++) e[i].clear(), in[i] = 0;
    for (int i = 1; i <= mid; i++)
        for (int j = 1; j < c[i].size(); j++) {
            e[c[i][j - 1]].push_back(c[i][j]);
            in[c[i][j]]++;
        }
}
bool check() { // O(n)
    queue<int> q;
    for (int i = 1; i <= n; i++) if (in[i] == 0) q.push(i);
    int cnt = 0;
    while (!q.empty()) {
        int u = q.front(); q.pop();
        cnt++;
        for (int v : e[u]) if (--in[v] == 0) q.push(v);
    }
    return cnt == n;
}
bool topo() { // O(nlogn)
    priority_queue<int, vector<int>, greater<int> > q;
    for (int i = 1; i <= n; i++) if (in[i] == 0) q.push(i);
    while (!q.empty()) {
        int u = q.top(); q.pop();
        ans.push_back(u);
        for (int v : e[u]) if (--in[v] == 0) q.push(v);
    }
    return ans.size() == n;
}
int main() {
    cin >> n >> m;
    for (int i = 1, k; i <= m; i++) {
        cin >> k;
        while (k--) {
            int j; cin >> j;
            c[i].push_back(j);
        }
    }
    int l = 0, r = m, res = 0;
    while (l <= r) {
        int mid = (l + r) >> 1;
        build(mid);
        if (check()) res = mid, l = mid + 1;
        else r = mid - 1;
    }
    build(res);
    topo();
    for (int u : ans) cout << u << ' ';
    return 0;
}

菜肴制作

最优解不是字典序最小的排列，而是符合条件的排序中，反序列的字典序最大的排列。先反向建图，再跑用大根堆维护的拓扑排序，以保证每次删边后字典序大的往答案序列的前面放。最后逆向输出即可。

启示：拓扑排序无法决定一个点尽可能早地加入拓扑序列，只能保证一个点尽可能晚地加入拓扑序列。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 8;
int in[N], n, m, t;
vector<int> e[N], ans;
bool topo() {
    priority_queue<int> q;
    for (int i = 1; i <= n; i++) if (in[i] == 0) q.push(i);
    while (!q.empty()) {
        int u = q.top(); q.pop();
        ans.push_back(u);
        for (int v : e[u]) if (--in[v] == 0) q.push(v);
    }
    return ans.size() == n;
}
int main() {
    cin >> t;
    while (t--) {
        cin >> n >> m;
        for (int i = 1; i <= n; i++) in[i] = 0, e[i].clear();
        ans.clear();
        for (int i = 1, u, v; i <= m; i++) {
            cin >> u >> v;
            e[v].push_back(u);
            in[u]++;
        }
        if (topo()) {
            for (int i = n - 1; i >= 0; i--) cout << ans[i] << ' ';
            cout << "\n";
        } else cout << "Impossible!\n";
    }
    return 0;
}

排序

对前 \(x\) 条边跑拓扑排序后，若仍有点的入度为 \(0\) 则无解；若每次队列内只有 \(1\) 个元素则有唯一解。代码实现上主要有以下两种各有千秋的方法。

方法一：每次重新建图，不作 char 到 int 的映射。

#include <bits/stdc++.h>
using namespace std;
bool only;
int in[128], n, m;
string c[608], ans;
vector<char> e[128];
void build(int mid) {
    only = true, ans = "";
    for (char i = 'A'; i <= 'A' + n - 1; i++) in[i] = 0, e[i].clear();
    for (int i = 1; i <= mid; i++) {
        char u = c[i][0], v = c[i][2];
        e[u].push_back(v);
        in[v]++;
    }
}
bool topo() {
    queue<char> q;
    for (char i = 'A'; i <= 'A' + n - 1; i++) if (in[i] == 0) q.push(i);
    while (!q.empty()) {
        only &= (q.size() == 1);
        char u = q.front(); q.pop();
        ans += u;
        for (char v : e[u]) if (--in[v] == 0) q.push(v);
    }
    for (char i = 'A'; i <= 'A' + n - 1; i++) if (in[i] != 0) return false;
    return true;
}
int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) cin >> c[i];
    for (int i = 1; i <= m; i++) {
        build(i);
        if (!topo()) {
            cout << "Inconsistency found after " << i << " relations.";
            return 0;
        }
        if (only) {
            cout << "Sorted sequence determined after " << i << " relations: " << ans << '.';
            return 0;
        }
    }
    cout << "Sorted sequence cannot be determined.";
    return 0;
}

方法二：随着读入逐步建图并保存 base 值，作 char 到 int 的映射。

#include <bits/stdc++.h>
using namespace std;
bool only;
int in[32], base[32], n, m;
vector<int> e[32], ans;
bool topo() {
    queue<int> q;
    for (int i = 1; i <= n; i++) if (in[i] == 0) q.push(i);
    while (!q.empty()) {
        only &= (q.size() == 1);
        int u = q.front(); q.pop();
        ans.push_back(u);
        for (int v : e[u]) if (--in[v] == 0) q.push(v);
    }
    for (int i = 1; i <= n; i++) if (in[i] != 0) return false;
    return true;
}
int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        char u, _, v;
        cin >> u >> _ >> v;
        e[u - 'A' + 1].push_back(v - 'A' + 1);
        base[v - 'A' + 1]++;
        for (int i = 1; i <= n; i++) in[i] = base[i];
        only = true;
        ans.clear();
        if (!topo()) {
            cout << "Inconsistency found after " << i << " relations.";
            return 0;
        }
        if (only) {
            cout << "Sorted sequence determined after " << i << " relations: ";
            for (int u : ans) cout << char(u + 'A' - 1);
            cout << ".\n";
            return 0;
        }
    }
    cout << "Sorted sequence cannot be determined.";
    return 0;
}

DAG 上 DP

最大食物链计数

原问题可转化为：找到图中所有左端点入度为 \(0\)，右端点出度为 \(0\) 的链的数量。考虑在 DAG 上 DP，用拓扑排序维护状态依赖关系。设 \(f[i]\) 表示以第 \(i\) 个点结尾的链有多少条。若从拓扑排序的队头中取出一个点 \(u\)，对于 \(u\) 所能到达的点 \(v\) ，则有 \(f[v] \ += f[u]\)。最终答案即为出度为 \(0\) 的所有点的 \(f[i]\) 之和。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N = 5e3 + 8, P = 80112002;
int n, m, in[N], dp[N], out[N], ans;
vector<int> e[N];
void topo() {
    queue<int> q;
    for (int i = 1; i <= n; i++)
        if (in[i] == 0) {
            q.push(i);
            dp[i] = 1;
        }
    while (!q.empty()) {
        int u = q.front(); q.pop();
        for (int v : e[u]) {
            (dp[v] += dp[u]) %= P;
            if (--in[v] == 0) q.push(v);
        }
    }
}
int main() {
    cin >> n >> m;
    for (int i = 1, u, v; i <= m; i++) {
        cin >> u >> v;
        e[u].push_back(v);
        out[u]++; in[v]++;
    }
    topo();
    for (int i = 1; i <= n; i++)
        if (out[i] == 0) (ans += dp[i]) %= P;
    cout << ans;
    return 0;
}

Chocolate Milks

假定每个挤奶器的牛奶流量为 \(1\)，并且 \(f[i]\) 表示第 \(i\) 个点汇聚了来自多少个不同挤奶器的牛奶。进行拓扑排序，若某点的流量为挤奶器的数量，则该点可以放置巧克力混合器。

注意到“最多只有一种方式从一个接口流到另一个接口”，因此任意一个出度大于 \(1\) 的接口结点的子结点都不能放置巧克力混合器。具体地，可以用 \(vis\) 数组记录该点是不是挤奶器结点。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 8;
int n, in[N], dp[N], cnt;
bool vis[N];
vector<int> e[N], ans;
void topo() {
    queue<int> q;
    for (int i = 1; i <= n; i++)
        if (in[i] == 0) {
            cnt++;
            q.push(i);
            vis[i] = 1;
            dp[i] = 1;
        }
    while (!q.empty()) {
        int u = q.front(); q.pop();
        if (dp[u] == cnt && vis[u] == 0) ans.push_back(u);
        if (e[u].size() != 1) break;
        int v = e[u][0];
        dp[v] += dp[u];
        if (--in[v] == 0) q.push(v);
    }
}
int main() {
    cin >> n;
    for (int i = 1, u, v; i < n; i++) {
        cin >> u >> v;
        e[u].push_back(v);
        in[v]++;
    }
    topo();
    sort(ans.begin(), ans.end());
    for (int i : ans) cout << i << "\n";
    return 0;
}

车站分级

将停靠（等级低）的车站 \(u\) 向未停靠（等级高）的车站 \(v\) 连一条边，进行拓扑排序。设 \(f[i]\) 为第 \(i\) 个车站的最高等级，则 \(f[v] = \max \left\{ f[v], \ f[u] + 1 \right\}\)。注意建图时规避重边。

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 8;
int n, m, g[N][N], in[N], dp[N], ans;
void topo() {
    queue<int> q;
    for (int i = 1; i <= n; i++)
        if (in[i] == 0) {
            dp[i] = 1;
            q.push(i);
        }
    while (!q.empty()) {
        int u = q.front(); q.pop();
        for (int v = 1; v <= n; v++)
            if (g[u][v]) {
                dp[v] = max(dp[v], dp[u] + 1);
                if (--in[v] == 0) q.push(v);
            }
    }
}
int main() {
    cin >> n >> m;
    while (m--) {
        int s; cin >> s;
        vector<int> stp;
        bool vis[N] = {};
        while (s--) {
            int v; cin >> v;
            stp.push_back(v);
            vis[v] = true;
        }
        for (int u = stp[0]; u <= stp[stp.size() - 1]; u++)
            if (!vis[u])
                for (int v : stp)
                    if (!g[u][v]) {
                        g[u][v] = 1;
                        in[v]++;
                    }
    }
    topo();
    for (int i = 1; i <= n; i++) ans = max(ans, dp[i]);
    cout << ans;
    return 0;
}

最长不下降子序列

发现 \(1 \leq A_i \leq 10\)，不妨设 \(f[i][j]\) 表示从某点出发到达 \(i\) 满足末尾数字为 \(j\) 的最长不下降子序列长度，初始化 \(f[i][A[i]] = 1\)。对于点 \(v\) 的某一个前驱结点 \(u\)，分两种情况考虑转移。

\(\begin{cases} \forall 1 \leq i \leq A[v] &:& f[v][A[v]] = max(f[v][A[v]], \ f[u][i] + 1), & v \ is \ chosen \\ \forall 1 \leq i \leq 10 &:& f[v][i] = max(f[v][i], \ f[u][i]), & v \ isn't \ chosen \\ \end{cases}\)

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 8;
int n, m, a[N], dp[N][16], in[N];
vector<int> e[N];
void topo() {
    queue<int> q;
    for (int i = 1; i <= n; i++)
        if (in[i] == 0) {
            q.push(i);
            dp[i][a[i]] = 1;
        }
    while (!q.empty()) {
        int u = q.front(); q.pop();
        for (int v : e[u]) {
            for (int i = 1; i <= a[v]; i++)
                dp[v][a[v]] = max(dp[v][a[v]], dp[u][i] + 1);
            for (int i = 1; i <= 10; i++)
                dp[v][i] = max(dp[v][i], dp[u][i]);
            if (--in[v] == 0) q.push(v);
        }
    }
}
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1, u, v; i <= m; i++) {
        cin >> u >> v;
        e[u].push_back(v);
        in[v]++;
    }
    topo();
    int ans = 0;
    for (int i = 1; i <= n; i++) ans = max(ans, dp[i][a[i]]);
    cout << ans;
    return 0;
}

posted @ 2025-11-15 13:52 zheyutao 阅读(6) 评论(0) 收藏举报

刷新页面返回顶部

zheyutao

拓扑排序

定义

实现

例题

朴素拓扑

DAG 上 DP

公告