区间操作优化算法

1.树状数组

一般为求区间的和并统计某个特定值的数量，同时可以进行快速的在线更新。不算特别重要，简略带过。
看例题

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=300000;
int n,c[N],s[N];
struct lmy
{
	int x,y;
}site[N];
int lowbit(int x)
{
	return x&-x;
}
void add(int x,int val)
{
	//因为y有序，只需维护比较x的大小，只要后面的x大它就大 
	while(x<=32001)//用来维护比x小的星数有多少个 
	{
		c[x]+=val;
		x+=lowbit(x);
	}
}
int getsum(int x)
{
	int ans=0;
	while(x)
	{
		ans+=c[x];
		x-=lowbit(x);
	}
	return ans;
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d",&site[i].x,&site[i].y);
	}
	for(int i=1;i<=n;i++)
	{
		int a=site[i].x+1;
		int b=getsum(a);//求它前面有几颗星，即它为几级星 
		s[b]++;//它对应的星级数量+1 
		add(a,1); 
	}
	for(int i=0;i<n;i++)
	{
		printf("%d\n",s[i]);
	}
}

2.线段树

目前所用线段树为求区间的和，最值和维护对区间特定的操作，同样可以在线更新，对区间可以进行更多的操作，比树状数组适用范围大。给定范围求值

这道题用线段树进行操作维护的主要是区间左子树和右子树剩余空间的最大值，
举个例子：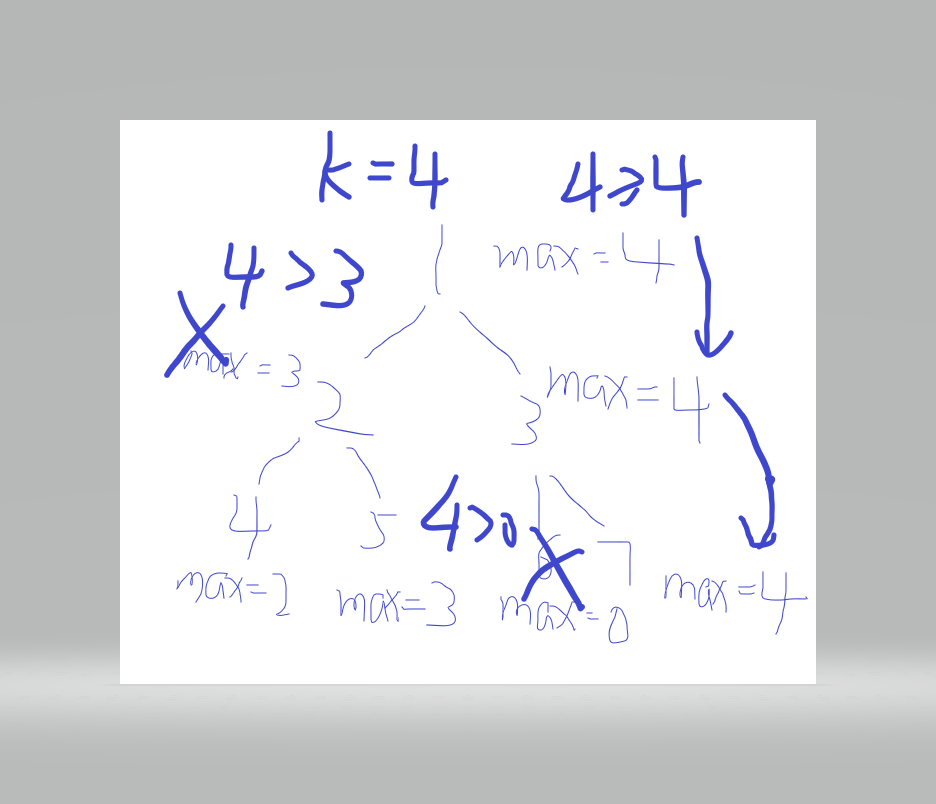

点击查看代码

#include<algorithm> 
#include<cstring> 
#include<cstdio> 
#include<cmath> 
using namespace std;
const int N=500000;
int h,w,n;
#define lson (rt<<1)
#define rson (rt<<1|1)
struct lmy
{
	int l,r;
	int max;
}tr[N<<2];

void build(int rt,int l,int r)
{
	tr[rt].l=l;
	tr[rt].r=r;
	if(l==r)
	{
		tr[rt].max=w;
		return ;
	}
	int mid=(l+r)>>1;
	build(lson,l,mid);
	build(rson,mid+1,r);
	tr[rt].max=max(tr[lson].max,tr[rson].max);
}
int answer(int rt,int val)
{
	if(tr[rt].l==tr[rt].r)
	{
		tr[rt].max-=val;//确定位置，减去占用空间
		return tr[rt].l;
	}
	int ans=0;
	if(tr[lson].max>=val)//要求结果相同i取最小，所以先遍历左子树
	{
		ans=answer(lson,val);
	}
	else
	{
		ans=answer(rson,val);
	}
	tr[rt].max=max(tr[lson].max,tr[rson].max);
	return ans;
}
int main()
{
	while(scanf("%d%d%d",&h,&w,&n)!=EOF)
	{
		h=min(h,n);
		memset(tr,0,sizeof(tr));
		build(1,1,h);
		int val;
		for(int i=1;i<=n;i++)
		{
			int ans=-1;
			scanf("%d",&val);
			if(val<=tr[1].max)
			{
				ans=answer(1,val);
			}
			printf("%d\n",ans);
		}
	}
}

3.单调栈和单调队列

其实可以只用单调队列，单调队列可以当做单调栈来用。
同样单调队列也可以维护一段区间的最值，并求出在特定要求下跟最值有关的范围，主要是求范围或给出范围求最值

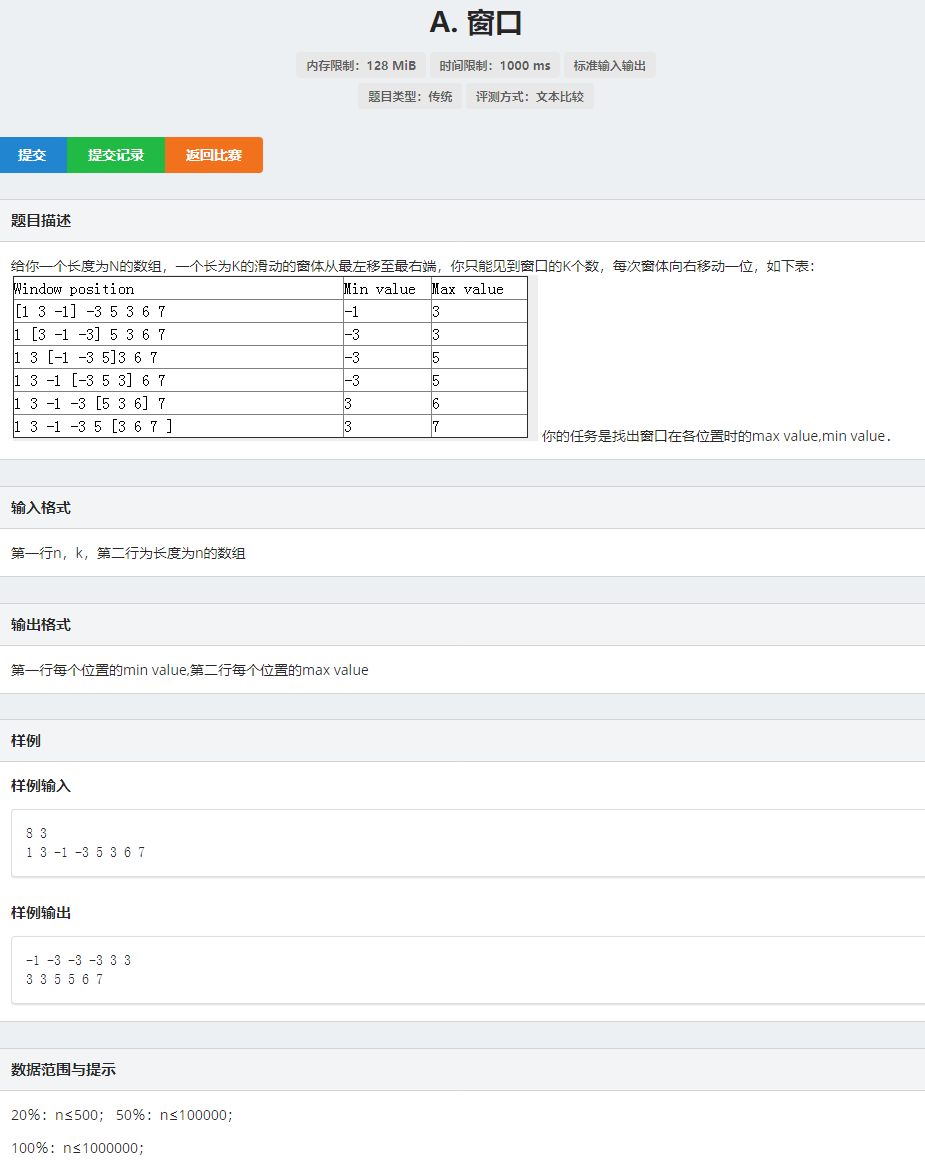
点击查看代码

#include<bits/stdc++.h>
using namespace std;

const int N=1000050;
int a[N],q[N];

int main()
{
	int n,k;
	scanf("%d%d",&n,&k);
	for(int i=0;i<n;i++)
	{
		scanf("%d",&a[i]);
	}
	int head=0,tail=-1;
	for(int i=0;i<n;i++)
	{
		if(head<=tail&&i-k+1>q[head])//超出范围的数减掉
		{
			head++;
		}
		while(head<=tail&&a[q[tail]]>=a[i])
		{
			tail--;
		}
		q[++tail]=i;//队列用来存储下标
		if(i>=k-1)
		{
			printf("%d ",a[q[head]]);
		}
	}
	printf("\n");
	head=0;
	tail=-1;
	for(int i=0;i<n;i++)
	{
		if(head<=tail&&i-k+1>q[head])
		{
			head++;
		}
		while(head<=tail&&a[q[tail]]<=a[i])
		{
			tail--;
		}
		q[++tail]=i;
		if(i>=k-1)
		{
			printf("%d ",a[q[head]]);
		}
	}
}