树状数组
树状数组基础模板
树状数组,顾名思义就是用树的结构来存储数据,树状数组支持的操作有区间修改和区间查询(单点也是可以),具体原理不再解释。
一维树状数组模板
点击查看代码
const int N=;
int c[N];//树状数组
int n;
int a[N];//存储数组
int lowbit(int x)
{
return x&-x;
}
void add(int x,int val)//a[x]+val
{
while(x<=n)
{
c[x]+=val;
x+=lowbit(x);
}
}
int getsum(int x)
{
int ans=0;
while(x)
{
ans+=c[x];
x-=lowbit(x);
}
return ans;
}
首先是单点修改和区间查询的操作
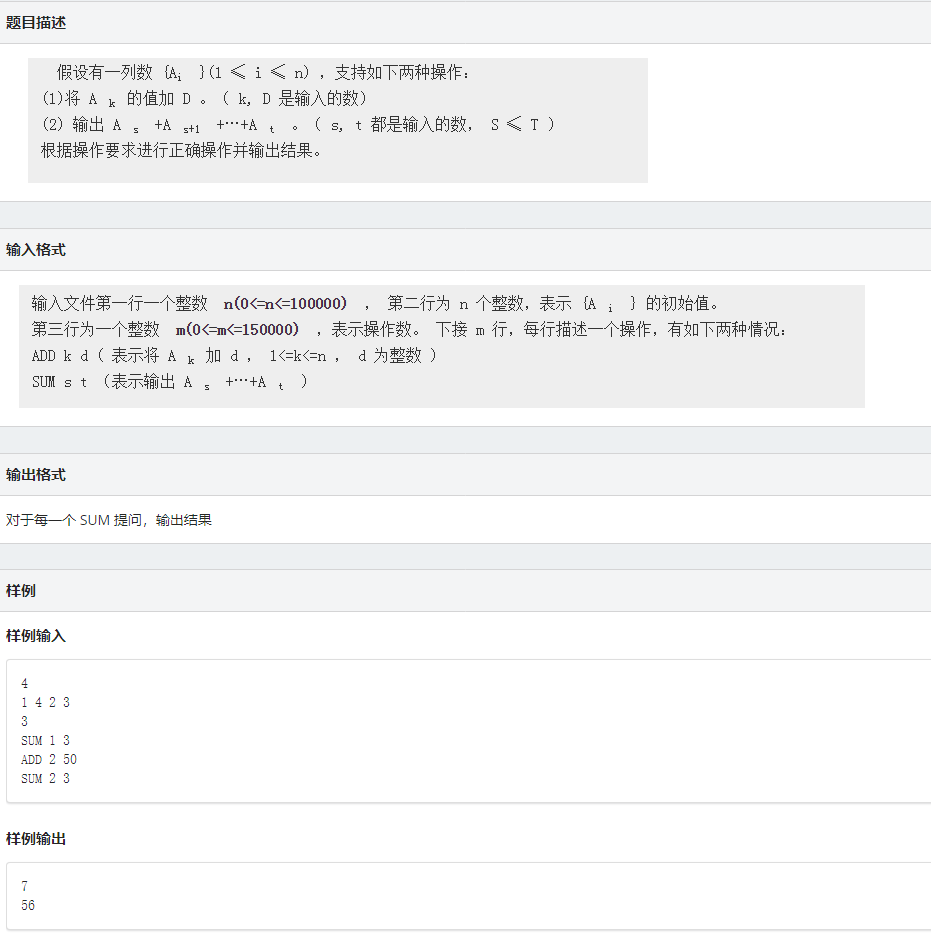
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int a[1000000],c[1000000];
int n,m;
int lowbit(int x)
{
return x&-x;
}
int getsum(int x)
{
int s=0;
while(x>0)
{
s+=c[x];
x-=lowbit(x);
}
return s;
}
void add(int x,int key)//a[x]+key
{
while(x<=n)
{
c[x]+=key;
x+=lowbit(x);
}
}
signed main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
add(i,a[i]);//修改(也可理解为初始化)
}
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
int x,y;
char ch[3];
scanf("%s",ch);
scanf("%d%d",&x,&y);
if(ch[0]=='S')
{
printf("%d\n",getsum(y)-getsum(x-1));//区间求和
}
if(ch[0]=='A')
{
add(x,y);//单点修改操作
}
}
}
区间修改和单点查询
这里需要用到一个小技巧,即用树状数组保存差值,这样区间修改的时候是修改整个区间,整个区间两数之间的差值不变,只需修改区间两边的差值,那单点查询的时候只需正常求和。
缘由:
c[1]=a[1]-a[0];//默认a[0]为0
c[2]=a[2]-a[1];
......
c[n]=a[n]-a[n-1];
因此要求a[2]只需c[1]+c[2]=a[2]-a[1]+a[1]-a[0]=a[2];
同理要求a[n]只需让c[1]+...+c[n],即区间求和。
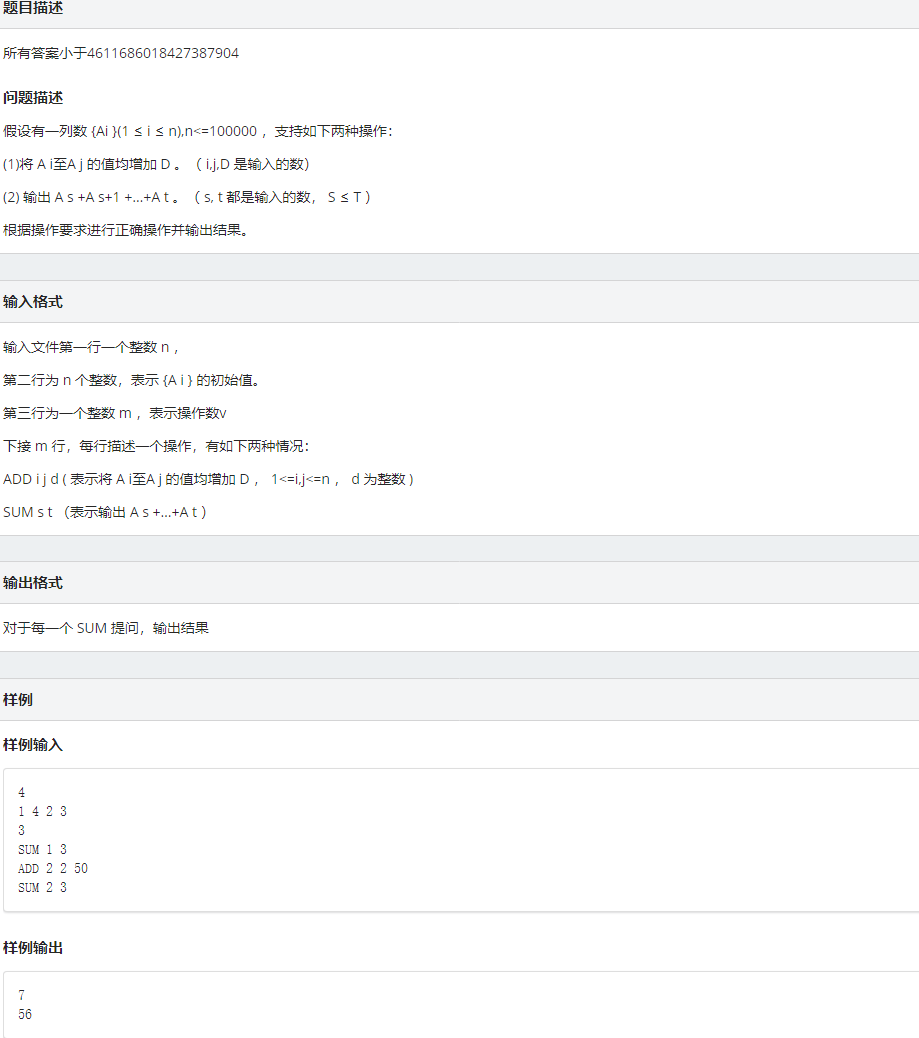
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
int sum[1000000],a[1000000],c1[1000000],c2[1000000];
int n,m;
int lowbit(int x)
{
return x&-x;
}
//简化版
//int getsum(int x)
//{
// int s=0;
// int i=x;
// while(i>0)
// {
// s+=(x+1)*c1[i]-c2[i];
// i-=lowbit(i);
// }
// return s;
//}
int getsum(int x)
{
int ans=0,ans1=0,ans2=0;
int i=x;
while(i>0)
{
ans1+=c1[i];
i-=lowbit(i);
}
ans1*=(x+1);
i=x;
while(i>0)
{
ans2+=c2[i];
i-=lowbit(i);
}
ans=ans1-ans2;
return ans;
}
void add(int x,int val)//a[x]+key
{
int i=x;
while(i<=n)
{
c1[i]+=val;
c2[i]+=x*val;//c2[]数组存 c1[i]*i
i+=lowbit(i);
}
}
signed main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
add(i,a[i]-a[i-1]);
}
scanf("%lld",&m);
for(int i=1;i<=m;i++)
{
int x,y,z;
char ch[5];
scanf("%s",ch);
if(ch[0]=='S')
{
scanf("%lld%lld",&x,&y);
printf("%lld\n",getsum(y)-getsum(x-1));
}
if(ch[0]=='A')
{
scanf("%lld%lld%lld",&x,&y,&z);
add(x,z);
add(y+1,-z);
}
}
}
到这里,树状数组的基本操作已经学会,区间查询,区间修改,单点查询,单点修改。
接下来看例题吧。
例题
HH的项链
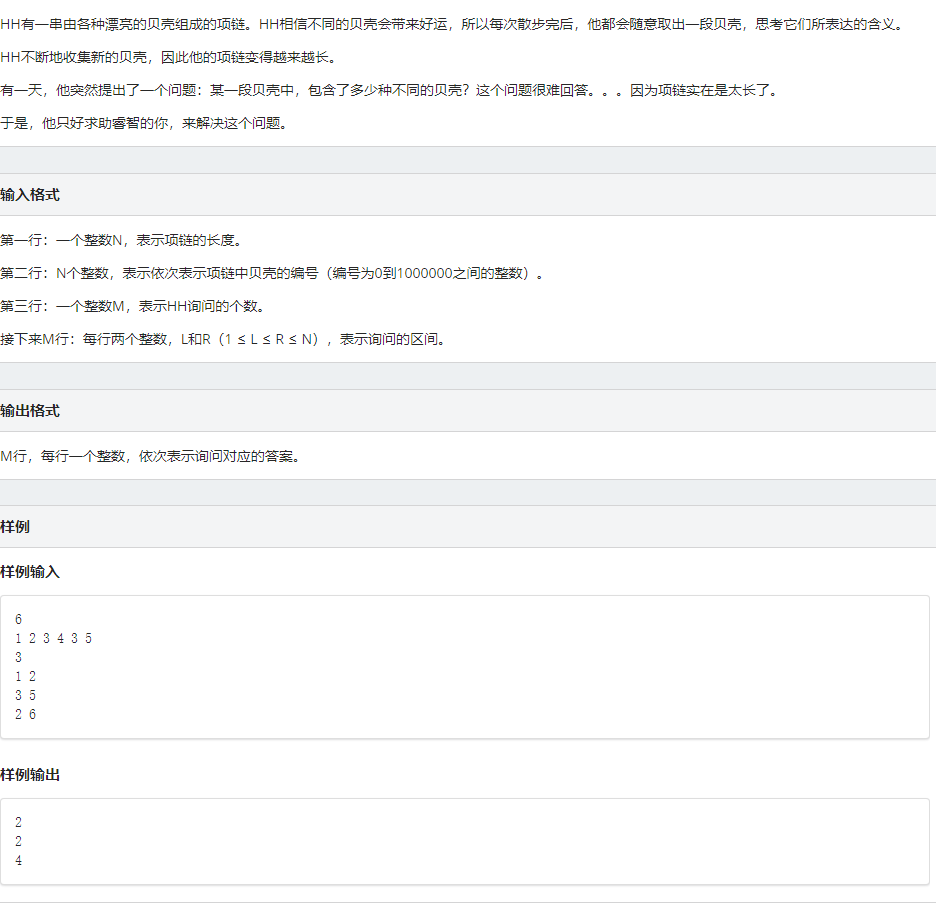
看到这题,我首先想到了用flag[]数组标记,很明显这是必需的。
但随着代码进行,又会遇到一个问题:如1 2 1 2,如果按照正常标记后面两个就不会被标记,那遍历3到4时,结果为0。
顺着思路想,如果我们在用完一次后把它丢掉,重新遍历,这也就导致我们必须要采用一种有序遍历,从而让前面的更新不会影响后面的结果,同时,我们也要每次更新完数据,自动计算结果并保存,后面更新就不再计算(离线)。到这,这道题的大体思路明了。
这里了解到几个新东西。
离线
在第一次更新到这个状态时,计算结果,即使后面再更新数据,也不再改变结果。
在线
每次数据更新,重新计算结果。
接下来就是代码了
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+6;
struct lmy//多个变量排序时可控
{
int l,r;
int id;
bool operator <(const lmy a)
{
return r<a.r;//以右边界大小排序
//遍历完后处理的数据不受影响
}
}q[N];
int a[N];
int mark[N];//mark[i]表示i上一次出现的位置
int c[N];
int ans[N];//保存结果
int n,m;
int lowbit(int x)
{
return x&-x;
}
void add(int x,int t)
{
while(x<=n)
{
c[x]+=t;
x+=lowbit(x);
}
}
int getsum(int x)
{
int ans=0;
while(x)
{
ans+=c[x];
x-=lowbit(x);
}
return ans;
}
int main()
{
ios::sync_with_stdio(0);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
cin>>m;
for(int i=1;i<=m;i++)
{
cin>>q[i].l>>q[i].r;
q[i].id=i;
}
sort(q+1,q+1+m);
int last=1;//上次查询的结尾+1
for(int i=1;i<=m;i++)
{
for(int j=last;j<=q[i].r;j++)
{
if(mark[a[j]])
//如果为0,它为第一个数
//不为0,则有上一个数
{
add(mark[a[j]],-1);//上一个数置0
}
add(j,1);
mark[a[j]]=j;//标记为上一个数
}
last=q[i].r+1;
ans[q[i].id]=getsum(q[i].r)-getsum(q[i].l-1);
}
for(int i=1;i<=m;i++)
{
cout<<ans[i]<<endl;
}
return 0;
}
数星星
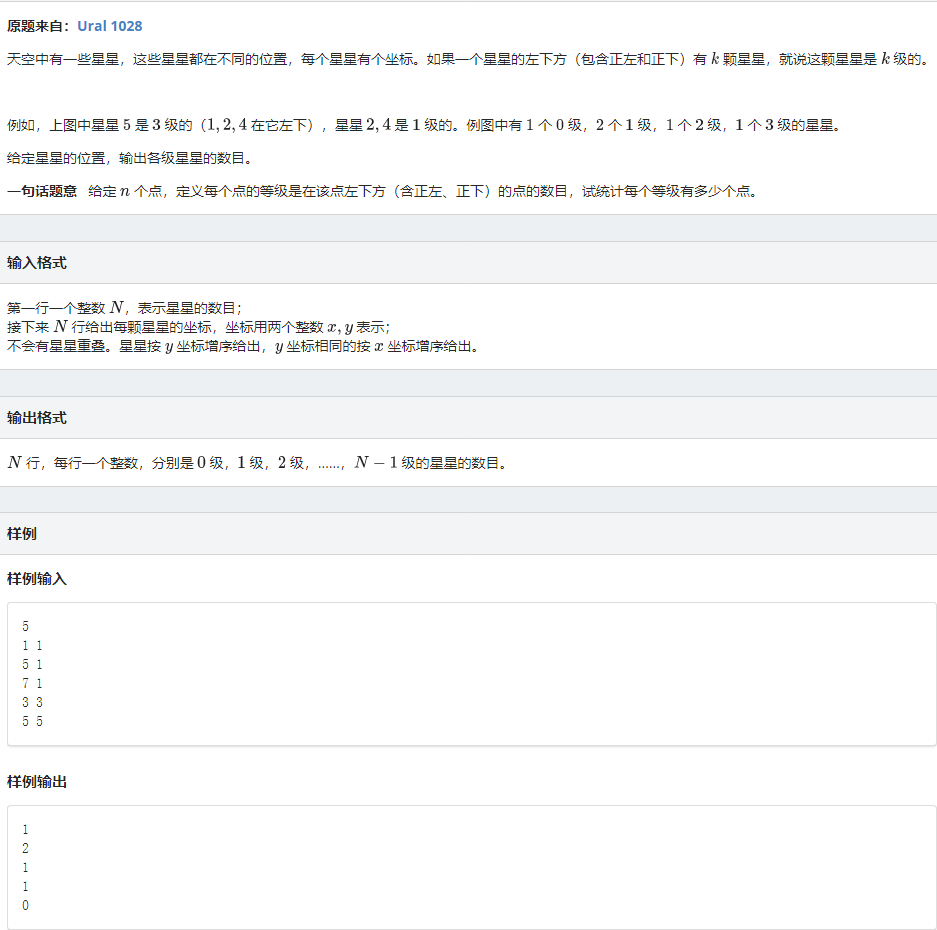
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=300000;
int n,c[N],s[N];
struct lmy
{
int x,y;
}site[N];
int lowbit(int x)
{
return x&-x;
}
void add(int x,int val)
{
//因为y有序,只需维护比较x的大小,只要后面的x大它就大
while(x<=32001)//用来维护比x小的星数有多少个
{
c[x]+=val;
x+=lowbit(x);
}
}
int getsum(int x)
{
int ans=0;
while(x)
{
ans+=c[x];
x-=lowbit(x);
}
return ans;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&site[i].x,&site[i].y);
}
for(int i=1;i<=n;i++)
{
int a=site[i].x+1;
int b=getsum(a);//求它前面有几颗星,即它为几级星
s[b]++;//它对应的星级数量+1
add(a,1);
}
for(int i=0;i<n;i++)
{
printf("%d\n",s[i]);
}
}
二维树状数组
模板
点击查看代码
int lowbit(int x)
{
return x&-x;
}
void add(int x,int y,int val)
{
for(int i=x;i<=n;i+=lowbit(i))
{
for(int j=y;j<=n;j+=lowbit(j))
{
c[i][j]+=val;
}
}
}
int getsum(int x,int y)
{
int ans=0;
for(int i=x;i>0;i-=lowbit(i))
{
for(int j=y;j>0;j-=lowbit(j))
{
ans+=c[i][j];
}
}
return ans;
}
内容与一维大致相同,不再赘述。
看例题吧
移动电话

点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=2000;
int n,c[N][N];
int op,x,y,z,l,b,r,t;
int lowbit(int x)
{
return x&-x;
}
void add(int x,int y,int val)
{
for(int i=x;i<=n;i+=lowbit(i))
{
for(int j=y;j<=n;j+=lowbit(j))
{
c[i][j]+=val;
}
}
}
int getsum(int x,int y)
{
int ans=0;
for(int i=x;i>0;i-=lowbit(i))
{
for(int j=y;j>0;j-=lowbit(j))
{
ans+=c[i][j];
}
}
return ans;
}
signed main()
{
while(1)
{
scanf("%d",&op);
if(op==3)
{
exit(0);
}
if(op==0)
{
scanf("%d",&n);
}
if(op==1)
{
scanf("%d%d%d",&x,&y,&z);
x++;
y++;
add(x,y,z);
}
if(op==2)
{
scanf("%d%d%d%d",&l,&b,&r,&t);
l++;
b++;
r++;
t++;
printf("%d\n",getsum(r,t)-getsum(l-1,t)-getsum(r,b-1)+getsum(l-1,b-1));
}
}
return 0;
}
这道题十分简单,不再多说,主要是关注一个小点,由于一维和二维中可能会出现0的情况,0的lowbit()为0,这导致在add()函数中x始终无法更新,在这时程序就会陷入死循环,于是我们在存入数据的时候就要++,来避免这种情况。
总结
树状数组是对数据存储和调用的一个优化,同时也是线段树的基础,难度适中,可放心食用。
到这了,拜拜




 浙公网安备 33010602011771号
浙公网安备 33010602011771号