坐标DP

坐标DP相较来说会比较简单。
直接上例题

1.坐标遍历问题
传纸条

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=120;
int m,n;
int g[N][N],f[N][N][N];
int ans;
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			cin>>g[i][j];
		}
	}
	for(int k=2;k<=n+m-1;k++)
	{
		for(int i1=1;i1<=n;i1++)
		{
			for(int i2=1;i2<=n;i2++)
			{
				int j1=k+1-i1;
				int j2=k+1-i2;
				if(j1<1||j2<1)
				{
					continue;
				}
				if(i1==i2)
				{
					continue;
				}
				ans=max(f[k-1][i1-1][i2-1],f[k-1][i1-1][i2]);
				ans=max(ans,f[k-1][i1][i2-1]);
				
				f[k][i1][i2]=max(ans,f[k-1][i1][i2])+g[i1][j1]+g[i2][j2];
								 
			}
		}
	}
	cout<<f[n+m-2][n][n-1];
}

这是优化后的代码，其中k代表的是步数，根据题易知从左上到右下所需步数总共为m+n-1，同样我们只需知道步数和它的横坐标，就可以求出它的纵坐标，因此我们只需记录三个变量就可以得到结果。

2.构成问题
接下来是坐标DP比较重要的题型，构成问题。

三角蛋糕

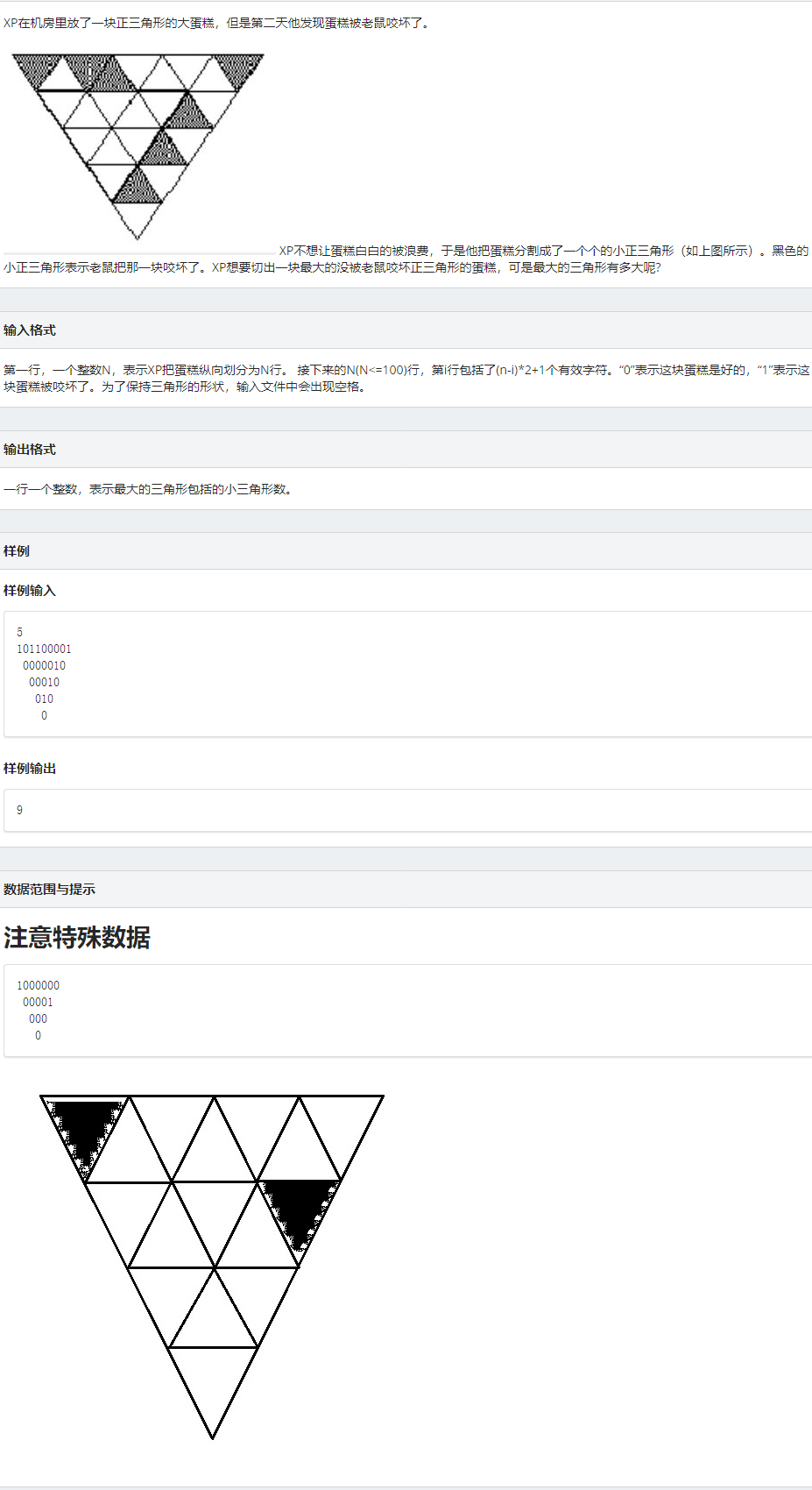
首先它想要构成2层正三角形，就需要它下面三个三角形没坏，想要构成3层正三角形就需要它每个下面的下面三个三角形没坏，以此类推，我们只需要遍历时为能构成多层的正三角形标记，只要它下面三个三角形没坏，就标记成1，如果它下面的三个三角形都标记成1就给它标记成2（注意三个三角形标记数可能不同，要取最小）。这就是代码的底层逻辑。
接下来就是处理一下细节，一个是正序遍历倒着的三角形，倒序遍历正着的三角形，同时注意作为顶的三角形正倒情况。好了，剩下的就没什么了，看代码吧。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=3000; 
int n,ans,cnt; 
char g[N][N];
int f[N][N],c[N][N];
int main()
{
    cin>>n;
	for(int i=1;i<=N-1;i++)
	{
		for(int j=1;j<=N-1;j++)
		{
			g[i][j]='1';
		}
	 } 
	 
    for(int i=1;i<=n;i++)
    {
    	for(int j=i;j<=(n-i)*2+i;j++)
    	{
    		
			cin>>g[i][j];
			if(g[i][j]=='1')
			{
				cnt++;
			}
		}
	}
	if(cnt==n*(n*2)/2)
	{
		cout<<0;
		exit(0);
	}
	for(int i=1;i<=n;i++)
    {
    	for(int j=i;j<=(n-i)*2+i;j++)
    	{
				if(g[i][j]=='0'&&g[i-1][j-1]=='0'&&g[i-1][j]=='0'&&g[i-1][j+1]=='0')
				{
//					cout<<i<<" "<<j; 
					int num=0x3f3f3f3f;
					num=min(f[i-1][j-1],num);
					num=min(f[i-1][j],num);
					num=min(f[i-1][j+1],num);
					f[i][j]=max(f[i][j],num+1);
				}		
		}
	}
	for(int i=n;i>=1;i--)
    {
    	for(int j=i;j<=(n-i)*2+i;j++)
    	{
				if(g[i][j]=='0'&&g[i+1][j-1]=='0'&&g[i+1][j]=='0'&&g[i+1][j+1]=='0')
				{
					int num=0x3f3f3f3f;
					num=min(c[i+1][j-1],num);
					num=min(c[i+1][j],num);
					num=min(c[i+1][j+1],num);
					c[i][j]=max(c[i][j],num+1);
				}		
		}
	}
	for(int i=1;i<=n;i++)
    {
    	for(int j=i;j<=(n-i)*2+i;j++)
    	{
    		if((j-i+1)&1)
    		{
//    			cout<<i<<" "<<j<<" ";
    			ans=max(ans,f[i][j]);
			}
			if((j-i+1)%2==0)
			{
				ans=max(ans,c[i][j]);
			}
		}
//		cout<<endl;
	}
//	cout<<ans<<" ";
	int s=(ans+1)*(1+(ans+1)*2-1)/2;
	cout<<s;
}

盖房子

（同上）不详细解析了

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=3000; 
int n,m,ans,cnt;
int g[N][N],f[N][N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
    	for(int j=1;j<=m;j++)
    	{
    		cin>>g[i][j];
    		if(g[i][j]==0)
    		{
    			cnt++;
			}
		}
	}
	if(cnt==n*m)
	{
		cout<<0;
		exit(0);
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			if(g[i][j]==1&&g[i][j-1]==1&&g[i-1][j]==1&&g[i-1][j-1]==1)
			{
				int num=0x3f3f3f3f;
				num=min(num,f[i][j-1]);
				num=min(num,f[i-1][j]);
				num=min(num,f[i-1][j-1]);
				f[i][j]=max(num+1,f[i][j]);
			}
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			ans=max(ans,f[i][j]);
		}
	}
	cout<<ans+1;
}