线性DP

这篇主要涉及线性DP。

先介绍模型，求最长上升子序列。

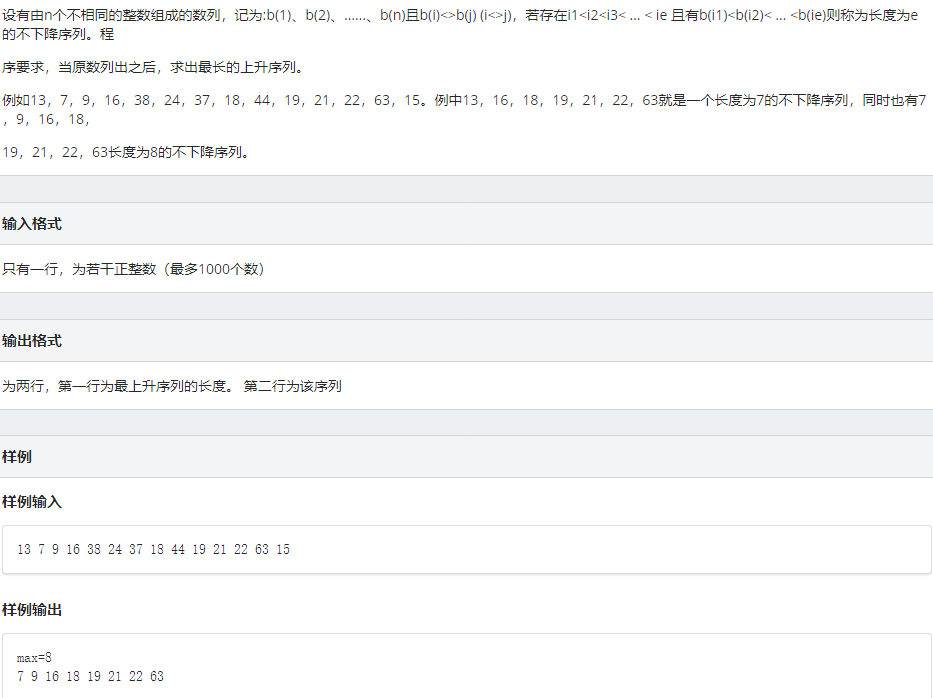
点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N=1020; 
int n;
int f[N],ans,a[N];
int pre[N],te;
void output(int x)
{
	if(x==0)
	{
		return;
	}
	
	output(pre[x]);
	cout<<a[x]<<" ";
}
int main()
{	 
	int x=0;
	while(scanf("%d",&x)!=EOF)
	{
		n++;
		a[n]=x;
	}
	for(int i=1;i<=n;i++)
	{
		f[i]=1;
		for(int j=1;j<i;j++)
		{
			if(a[i]>a[j]&&f[i]<f[j]+1)
			{
				f[i]=f[j]+1;
				pre[i]=j;
				if(ans<f[i])
				{
					ans=f[i];
					te=i;
				}
			}
		}
	
		
	}
	cout<<"max="<<ans<<endl;
	output(te);
	return 0;
}

其中也涉及了之前背包所用的路径标记。

下面来两个例题

拦截导弹

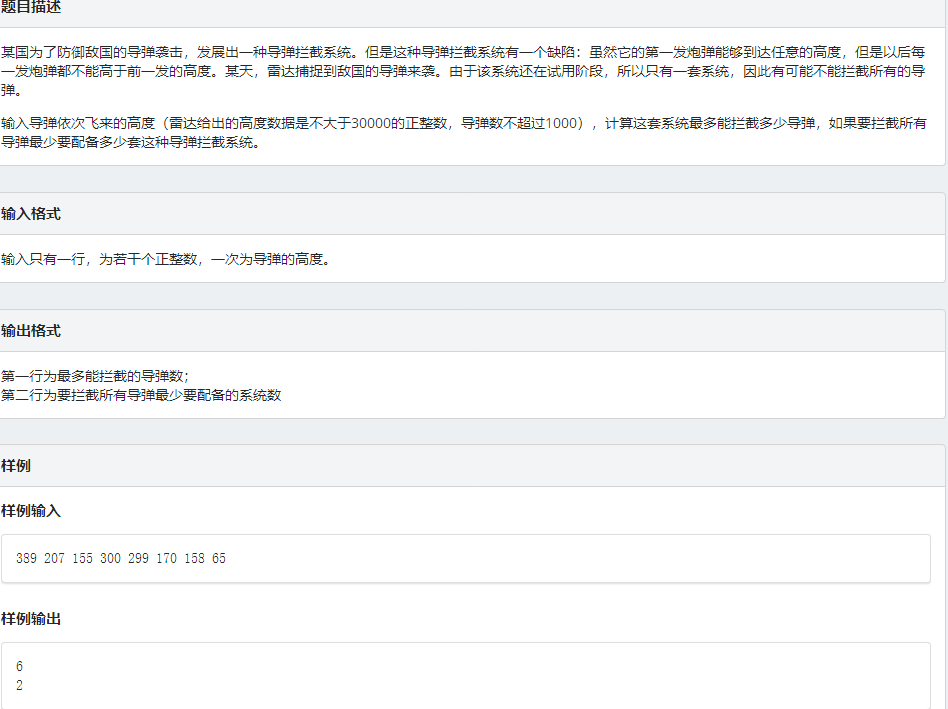
点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N=1020; 
int n;
int f[N],ans,cnt,num,a[N],b[N];
int pre[N],te;
int main()
{	 
	int x;
	while(scanf("%d",&x)!=EOF)
	{
		cnt++;
		a[cnt]=x;
	} 
	for(int i=1;i<=cnt;i++)
	{
		f[i]=1;
		for(int j=1;j<=cnt;j++)
		{
			if(a[i]<=a[j]&&f[i]<f[j]+1)
			{
				f[i]=f[j]+1;
			}
		}
		ans=max(ans,f[i]);
	} 
	for(int i=1;i<=cnt;i++)
	{
		b[i]=1;
		for(int j=1;j<i;j++)
		{
			if(a[i]>a[j])
			{
				b[i]=max(b[i],b[j]+1);
			}
		}
		num=max(num,b[i]);
	 } 
	cout<<(ans+1)/2<<endl<<num;
}

飞翔

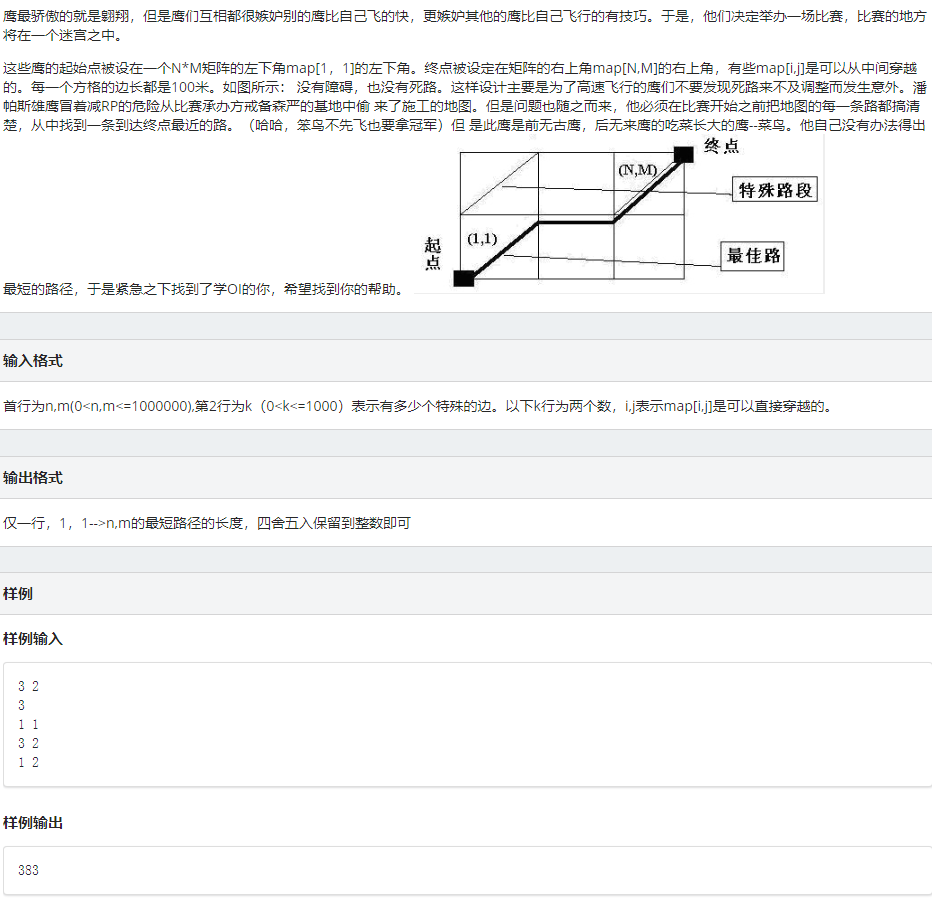
点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=1500;
const int Inf=0x3f3f3f3f;
int dp[maxn];
int sum;
double ans;
struct node
{
	int x,y;
}a[maxn];
bool cmp(node a,node b)
{
	return a.x<b.x;
}
int main()
{
	int n,m,k;
	cin>>n>>m>>k;
	for(int i=1;i<=k;i++)
	{
		cin>>a[i].x>>a[i].y;
	}	
	sort(a+1,a+k+1,cmp);
	for(int i=1;i<=k;i++)
	{
		for(int j=i+1;j<=k;j++)
		{
			if(a[j].x>a[i].x && a[j].y>a[i].y && dp[i]+1>dp[j])
			dp[j]=dp[i]+1;
		}
			
	}
		
	for(int i=1;i<=k;i++)
	{
		sum=max(dp[i],sum);	
	}	
	sum++;
	double len=2-sqrt(2);
	ans=(m+n-sum*len)*100;
	printf("%.0lf",ans); 
	return 0;
}

还算简单吧，接下来步入正题，看看真正的线性DP。

1.与图论相关联的线性DP

挖地雷

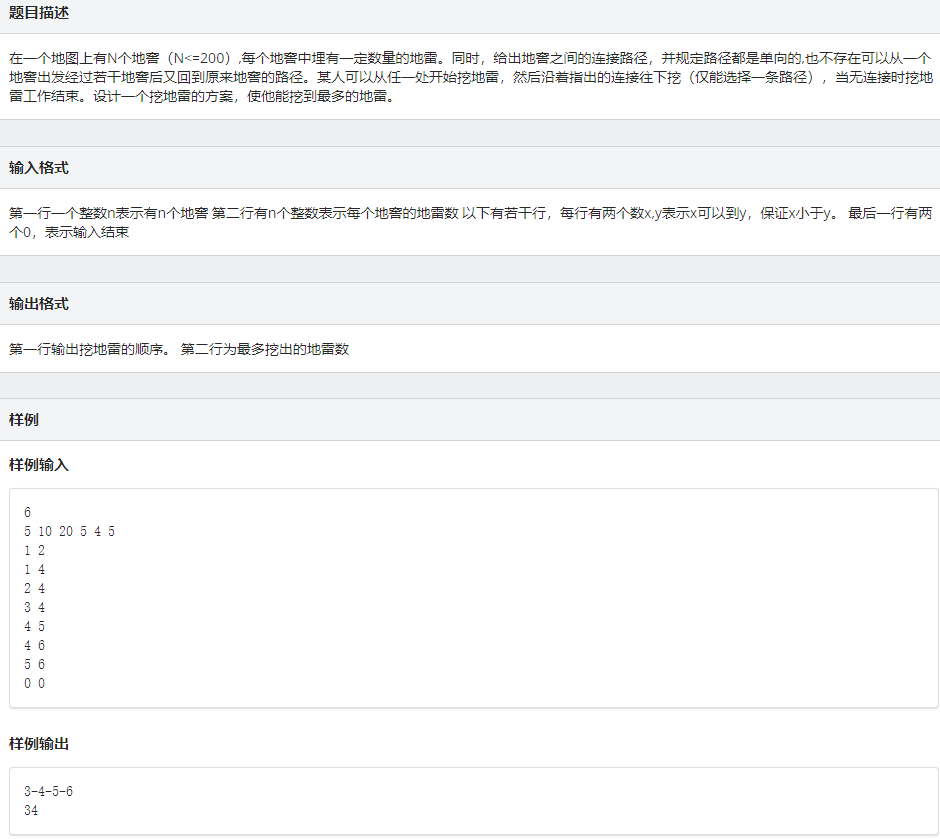
点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N=250; 
int n;
int f[N],ans,cnt,num,a[N],b[N];
int pre[N],g[N][N],s[N],flag[N];
int main()
{	 
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		f[i]=a[i];
		ans=max(ans,f[i]); 
	}
	int x,y;
	while(1)
	{
		cin>>x>>y;
		 
		if(x==0&&y==0)
		{
			break;
		}
		g[x][y]=1;//利用邻接矩阵存储有向图 
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(g[i][j]==1)
			{
				if(f[j]<f[i]+a[j]) 
				{
					f[j]=f[i]+a[j]; 
					s[j]=i;//追踪 
				}
				ans=max(ans,f[j]);	
			}
		}	
	}
	int m=ans;
	for(int i=1;i<=n;i++)
	{
		if(m==f[i])//标记 
		{
			m=i;
			break;
		}
	}
	while(m)
	{
		
		flag[m]=1;
		m=s[m];
		if(m==s[m])
		{
			break;
		}
	}
	for(int i=1;i<=n;i++)
	{
		if(flag[i]==1&&cnt==0)//遍历 
		{
			cout<<i;
			cnt=1;
		}
		else if(flag[i]==1)
		{
			cout<<"-"<<i;
		}
	}
	cout<<endl;
	cout<<ans;
}

注意同样的标记路径法

打鼹鼠

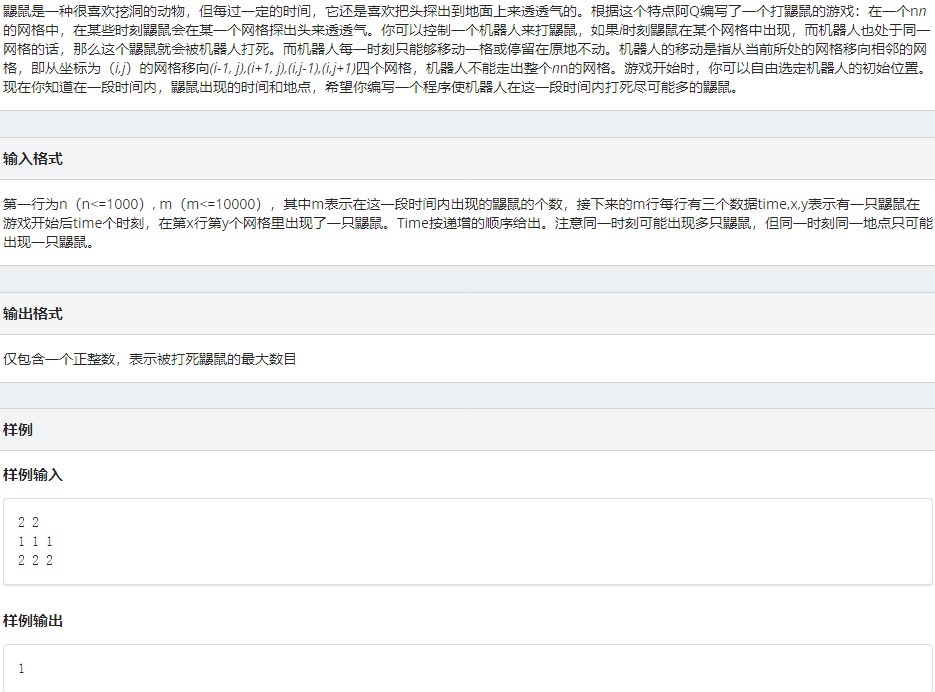
点击查看代码

#include<bits/stdc++.h>
using namespace std;

#define N 10005
int n, m, ti, x, y, dis,ans;
int dp[N];
struct mouse{
	int ti, x, y;
}mi[N];
int l(mouse a, mouse b);
int main(){
	cin >> n >> m;
	for(int i=1; i<=m; i++){
		cin >> mi[i].ti >> mi[i].x >> mi[i].y;
		dp[i] = 1;
	}
	for(int i=1; i<=m; i++){
		
		for(int j=i+1; j<=m; j++){
			int len = l(mi[i], mi[j]);
			if(len <= mi[j].ti - mi[i].ti){
				dp[j] = max(dp[j], dp[i] + 1);
				ans=max(ans,dp[j]);
			}
		}
		
	}
	cout << ans;
	return 0;
}

int l(mouse a, mouse b){
	return abs(a.x - b.x) + abs(a.y - b.y);
}

2.贪心的线性DP
只是与贪心算法类似，但并不能等同于贪心。

奶牛渡河（也不知道为什么这么喜欢奶牛）

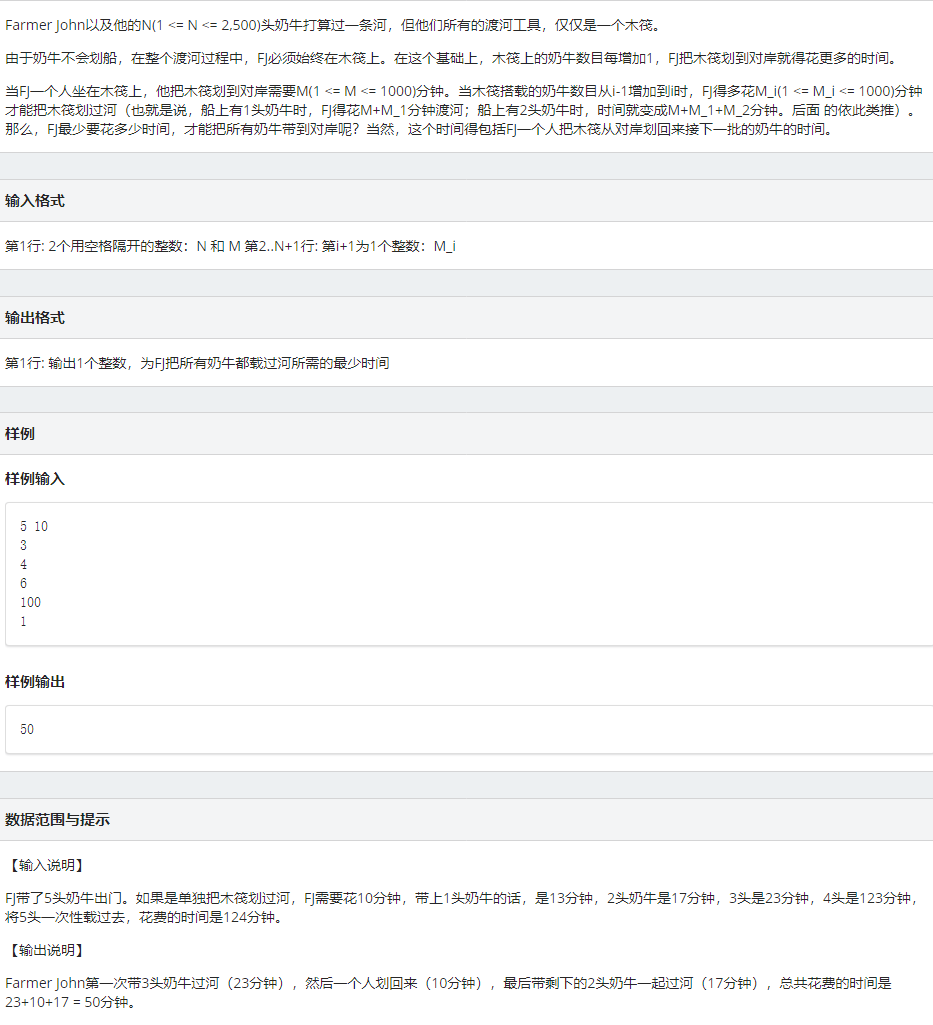
点击查看代码

#include<bits/stdc++.h> 
using namespace std;
const int N=2600;
int n,m,ans=1000000;
int f[N],a[N],s[N];
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		s[i]=s[i-1]+a[i]; 
	}
	for(int i=1;i<=n;i++)
	{
		f[i]=s[i]+m;
		for(int j=1;j<i;j++)
		{
			f[i]=min(f[i],f[j]+f[i-j]+m);
		}
	} 
	cout<<f[n];
}

总结
这些题都没什么好说的，只要能找对状态转移方程就很好理解。
因此在线性DP中最主要的地方就在于找出状态转移方程（无它，唯手熟耳，多练练题，就容易搞懂）。
线性DP就到这里了，拜拜