题解：CF1178D Prime Graph

随机跳到的题，做完发现解法和第一篇的思路一模一样，有点激动，写篇题解。

题意

构造一个有 $n$ 个节点的简单图，满足：

• 边数 $m$ 为质数。
• 所有点的度数均为质数。

思路

我们容易发现，若构造成一个环，每个点的的度数为 $2$，满足了第二点：

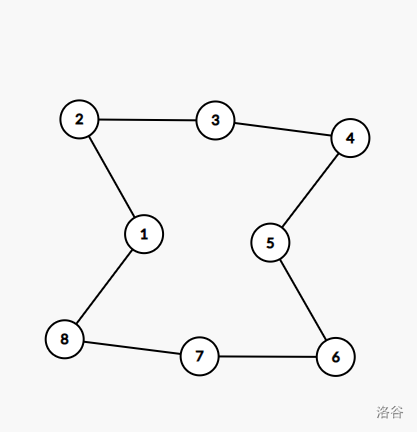
容易发现若再连一条边，两个点的度数将会变为 $3$，仍为质数，我们能找到 $\lfloor \frac{n}{2} \rfloor$ 组点，由于素数较密的原因，我们可以找到合适的 $m$ 满足其为质数。图为如下：

Code:

#include<bits/stdc++.h>
using namespace std;
int n, now = 1;
struct graph{
	int u, v;
};
vector<graph> g;
bool prime(int x){
	if(x <= 1) return 0;
	for(int i = 2; i * i <= x; i ++) if(x % i == 0){
		return 0;
	}
	return 1;
}
int main(){
	cin >> n;
	if(n <= 2){
		cout << -1;
		return 0;
	}
	for(int i = 1; i <= n; i ++) g.push_back({i, i % n + 1});
	while(!prime(g.size())){//不为质数
		g.push_back({now, now + n / 2});//前一半与后一半相匹配，避免重复。
		now ++;
	}
	cout << g.size() << "\n";
	for(int i = 0; i < g.size(); i ++) cout << g[i].u << " " << g[i].v << "\n";
	return 0;
}

时间复杂度 $O(n+k)$，其中 $k$ 为小于 $n$ 的最大相邻素数之差，在本题的数据范围（$n\le 1000$）中，差最大为 $20$，两个质数分别是 $887$ 和 $907$，可以通过。