Confusion Matrix - ROC curve和PR curve有什么关系？

非常好的问题。ROC 曲线（Receiver Operating Characteristic curve）和 PR 曲线（Precision-Recall curve）确实有密切的关系——它们都用于评估二分类模型的性能，但关注的重点不同，因此在不同场景下的表现和解读也不同。下面我们系统地对比一下它们的关系与区别 👇

---

🧩 一、二者的定义

曲线	横轴	纵轴	关注重点
ROC曲线	FPR（False Positive Rate）	TPR（True Positive Rate = Recall）	模型的整体区分能力
PR曲线	Recall（召回率）	Precision（精确率）	模型在正样本检测上的准确性

---

⚙️ 二、计算关系

它们都来自模型在不同阈值下的预测结果：

• 对每个可能的分类阈值，模型会输出一组：

  • TP（真正例）、FP（假正例）、FN（假反例）、TN（真反例）

• 然后：

  • ROC 曲线点：

    • TPR = TP / (TP + FN)

    • FPR = FP / (FP + TN)

  • PR 曲线点：

    • Precision = TP / (TP + FP)

    • Recall = TP / (TP + FN)

可以看到：两者都依赖相同的 TP、FP、FN、TN 统计量，只是关注的指标组合不同。

---

📊 三、直观关系

• ROC 曲线更关注整体区分能力：
  它同时考虑了正类与负类的表现，对数据集的类别比例（正负样本不均衡）不敏感。
  因此 ROC-AUC 在类别极不平衡（比如正样本 <1%）时可能显得“过于乐观”。

• PR 曲线更关注正类预测质量：
  因为它直接看 Precision 与 Recall，所以对正负样本比例非常敏感。
  当正样本很稀少时，PR 曲线的变化能更真实地反映模型在正样本检测上的性能。

---

🧮 四、数学层面的联系

给定模型的预测分布：

• ROC 曲线和 PR 曲线都能从同一组 (TP, FP, FN, TN) 计算得到；

• 一条 ROC 曲线唯一确定一条 PR 曲线（反之亦然），前提是知道数据集的正样本比例（prevalence）。

公式关系（简略版）：

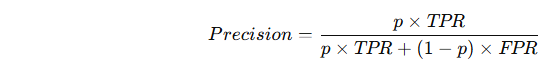
其中 ppp 是正样本比例（positive class prior）。

这说明：

✅ 如果你知道 ROC 曲线 + 样本分布，就能推导出 PR 曲线。
反之亦然，只要有足够信息。

---

📈 五、应用建议

场景	推荐指标	原因
正负样本数量相近	ROC-AUC	能全面衡量区分能力
正样本极少（如欺诈检测、疾病预测）	PR-AUC	更能体现正样本检测性能
想要看模型对“正样本”的表现	PR 曲线	关注 Precision 与 Recall 的平衡
想看模型的“整体区分能力”	ROC 曲线	不受类别比例影响

---

🧠 总结一句话：

• ROC 曲线：看模型整体区分能力，对类别不平衡不敏感。

• PR 曲线：看模型正类预测表现，在类别不平衡时更真实。

• 它们可以相互推导，但表达关注点不同。