 SVD
SVD

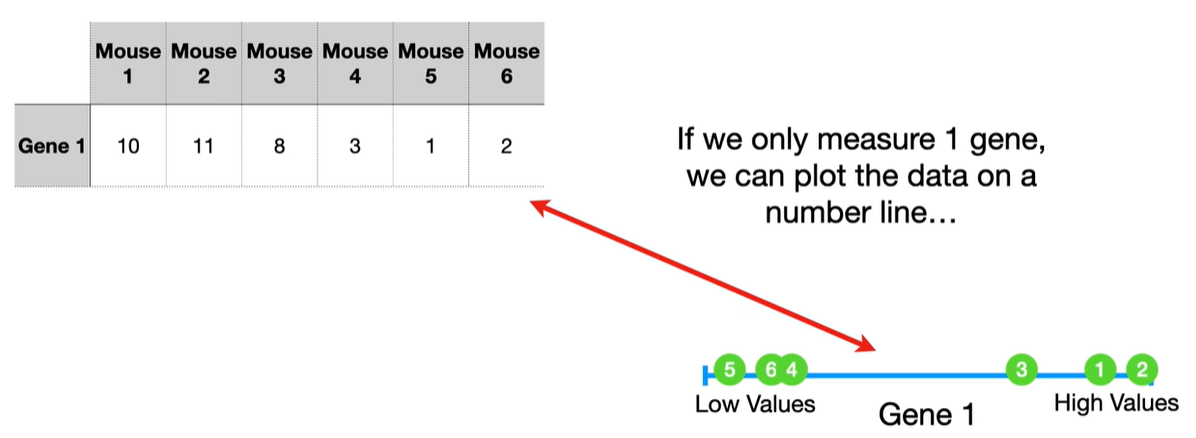
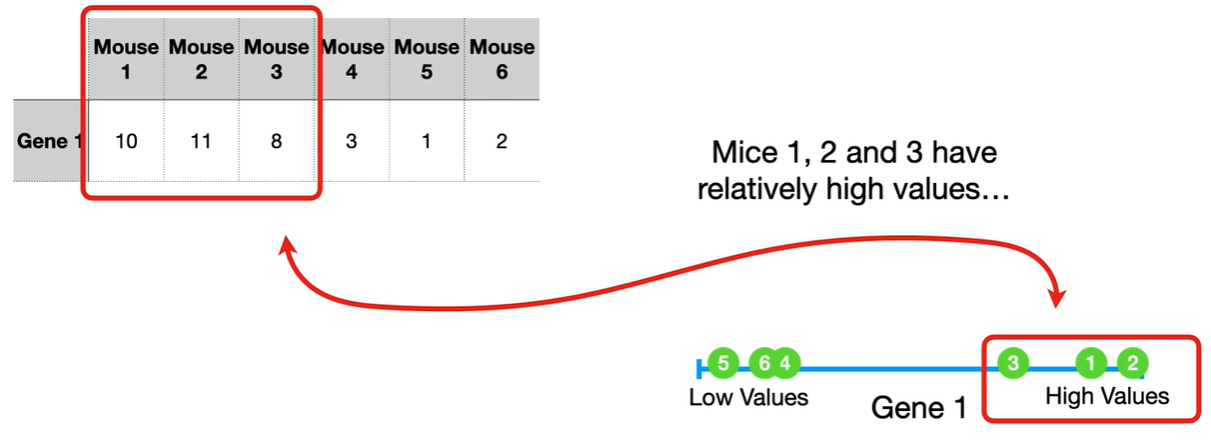



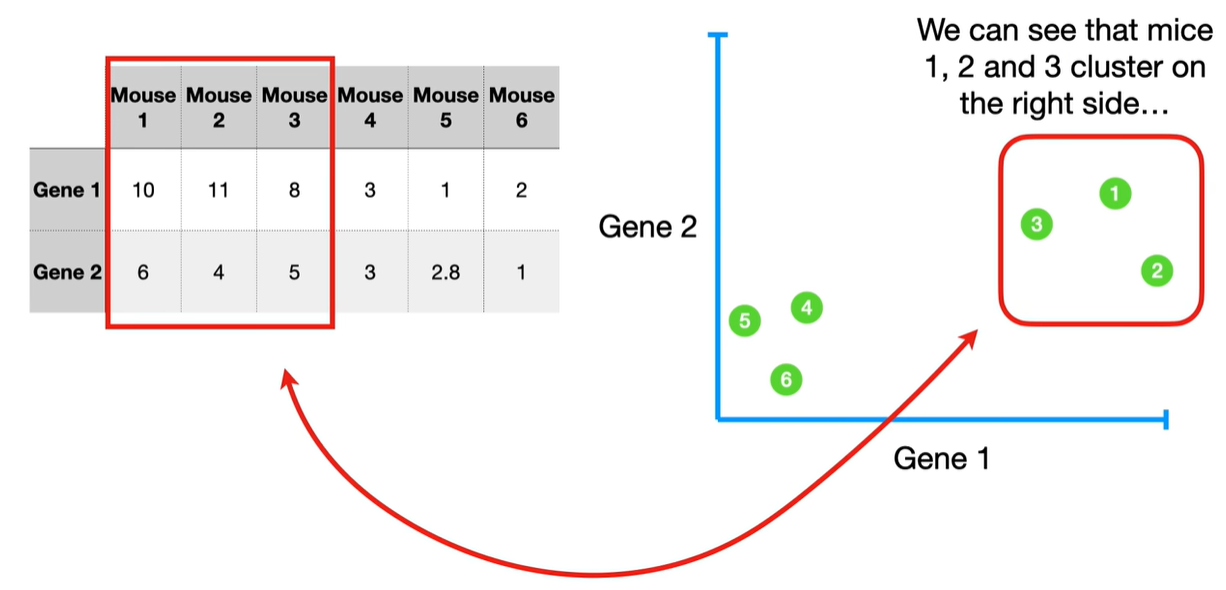
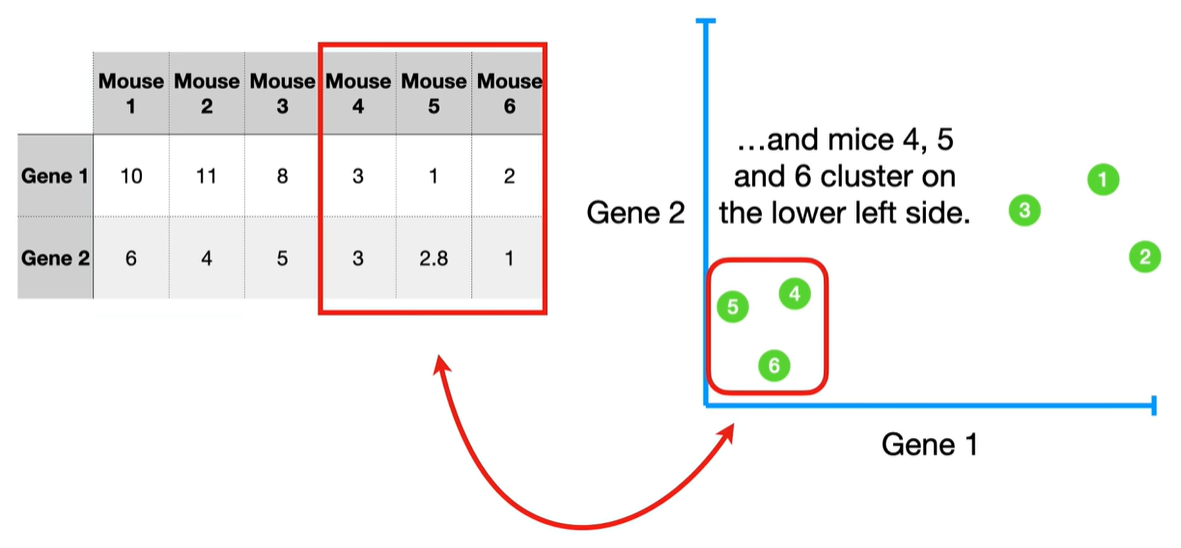




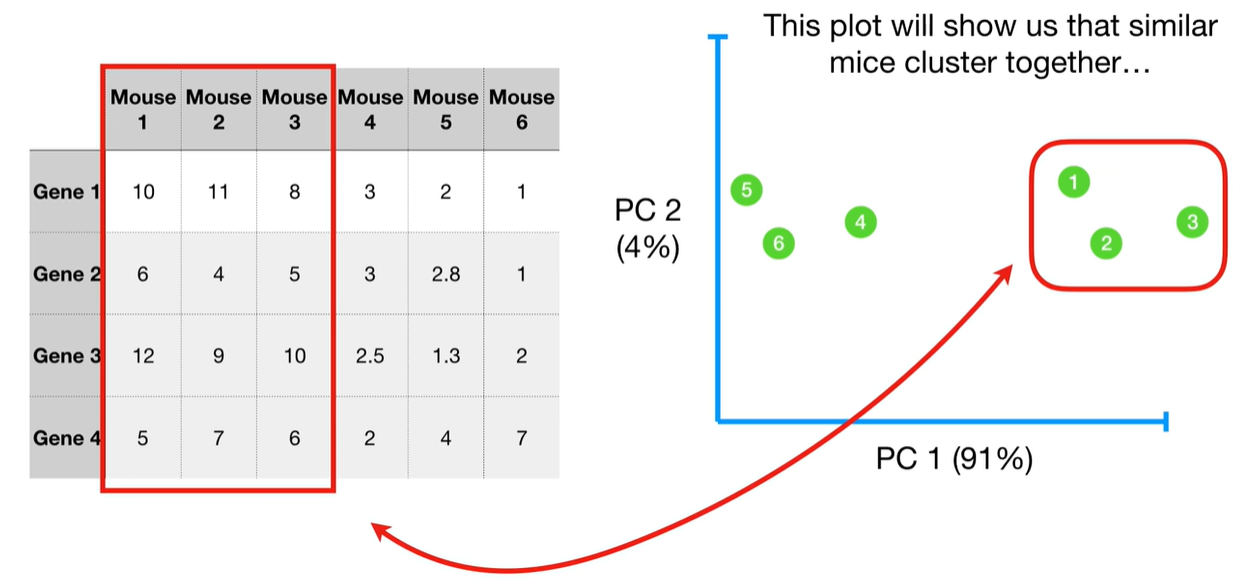


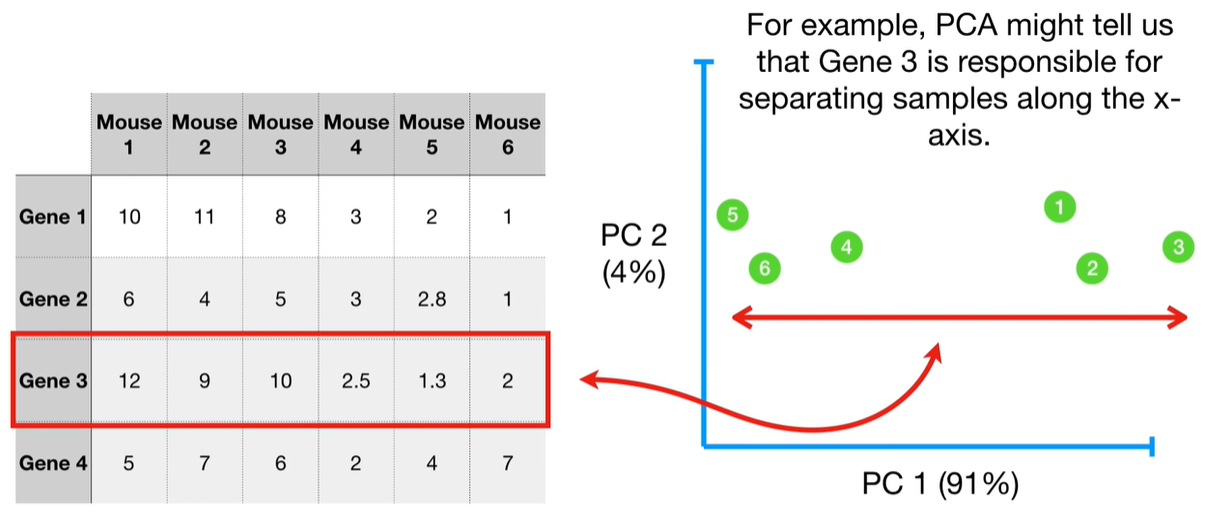




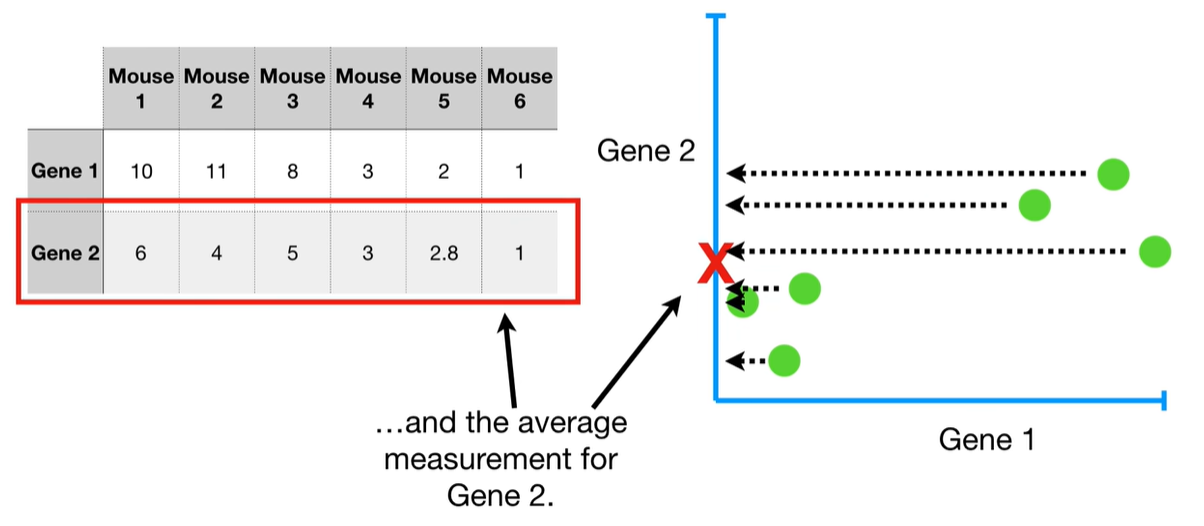
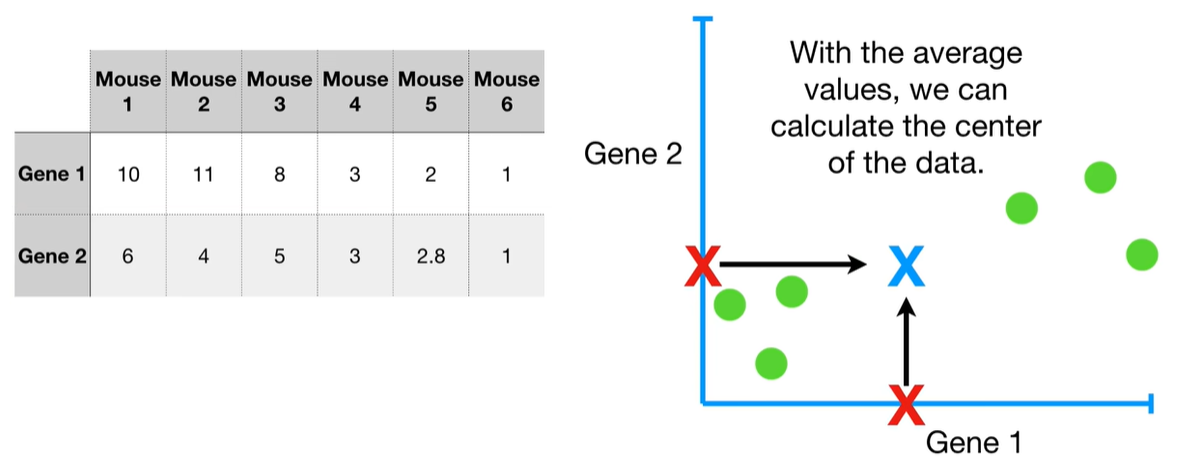
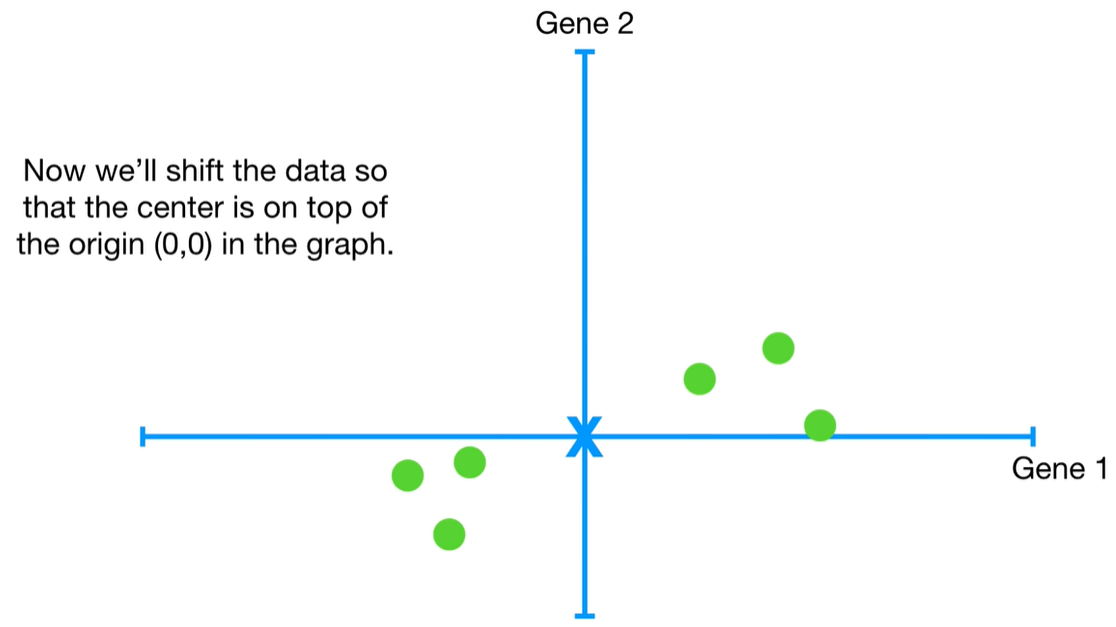

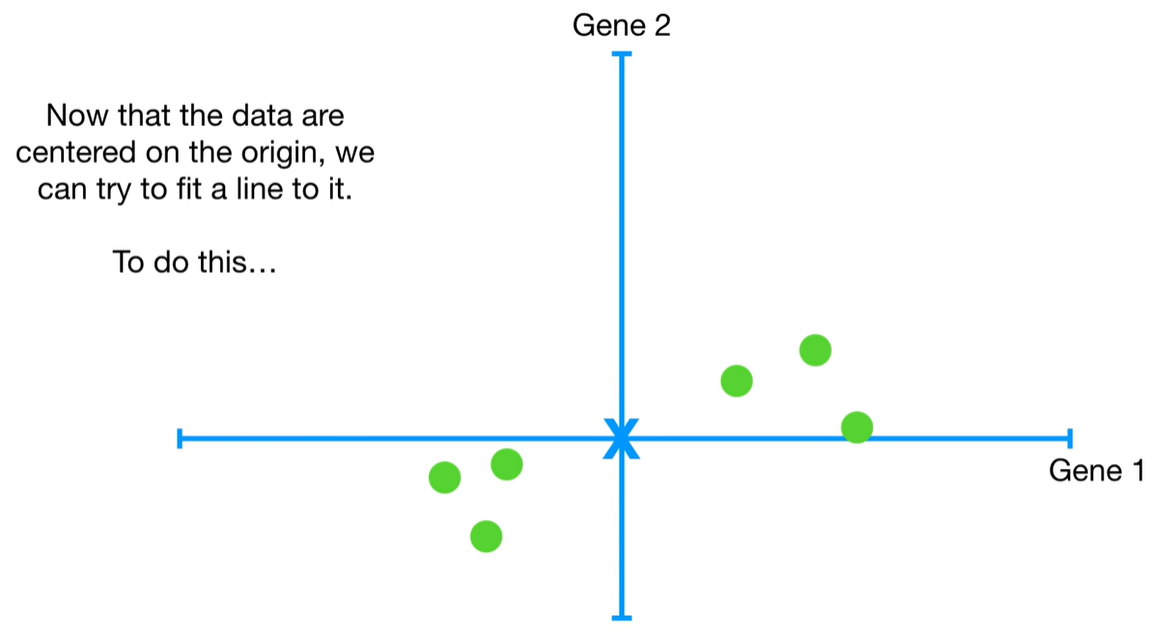
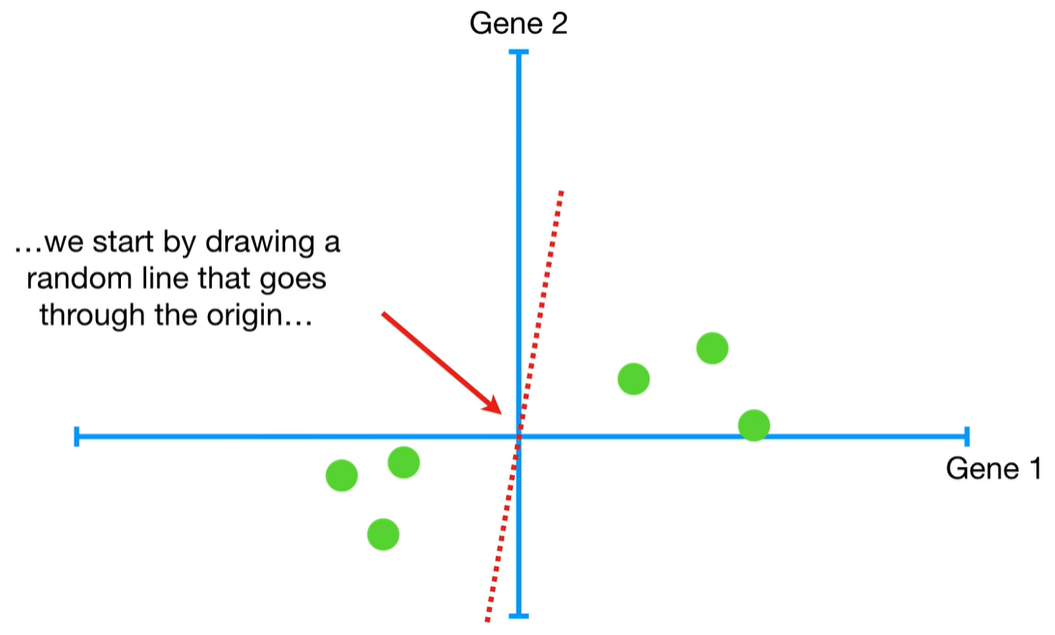
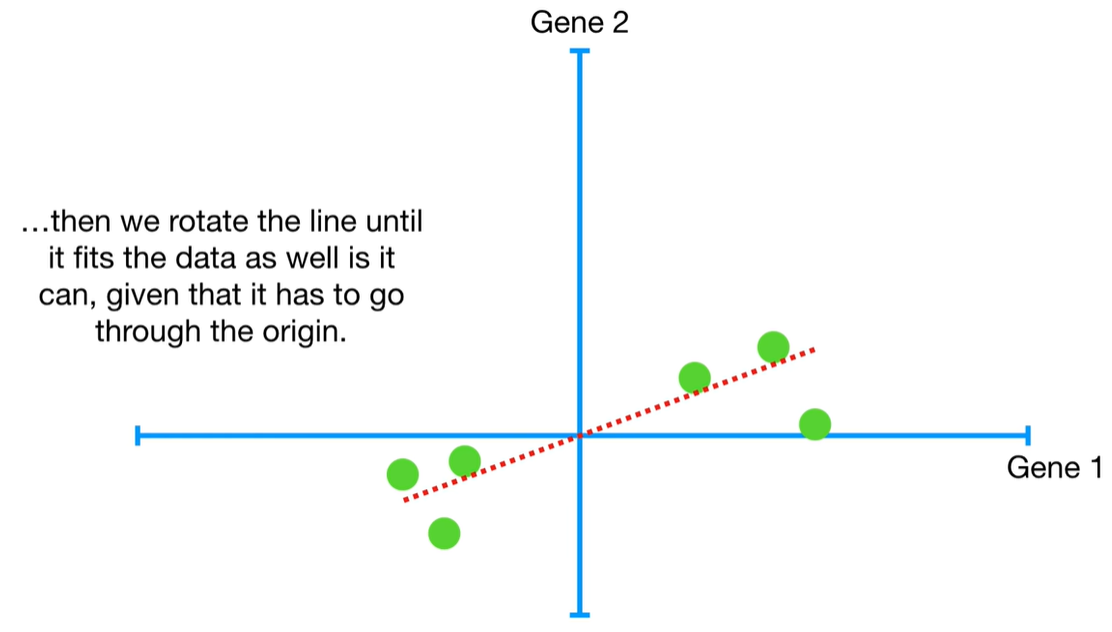
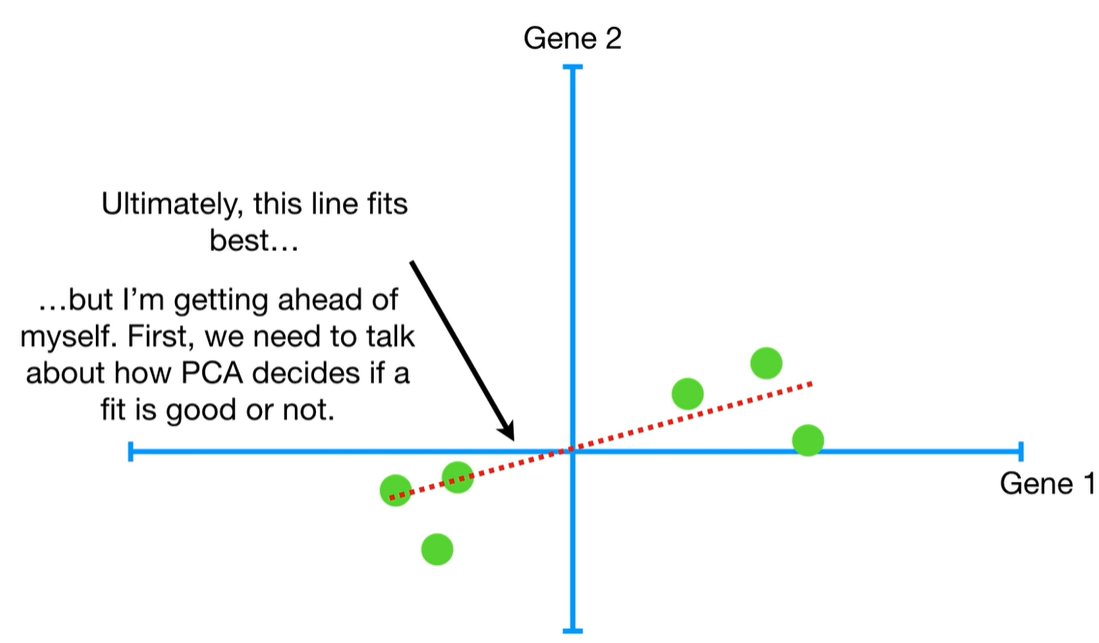
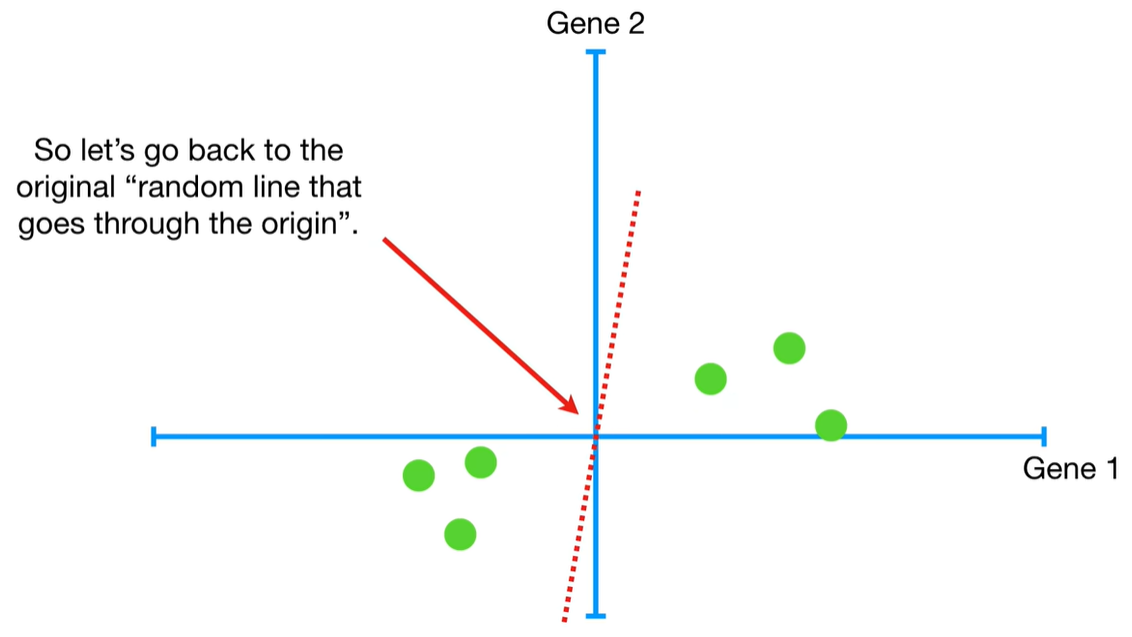
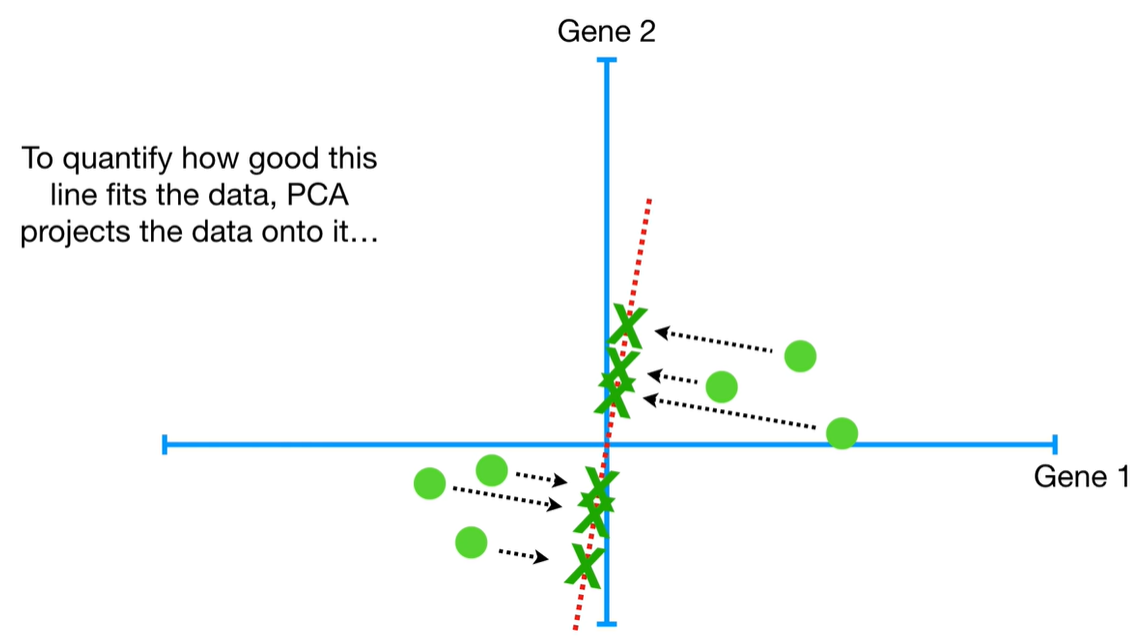
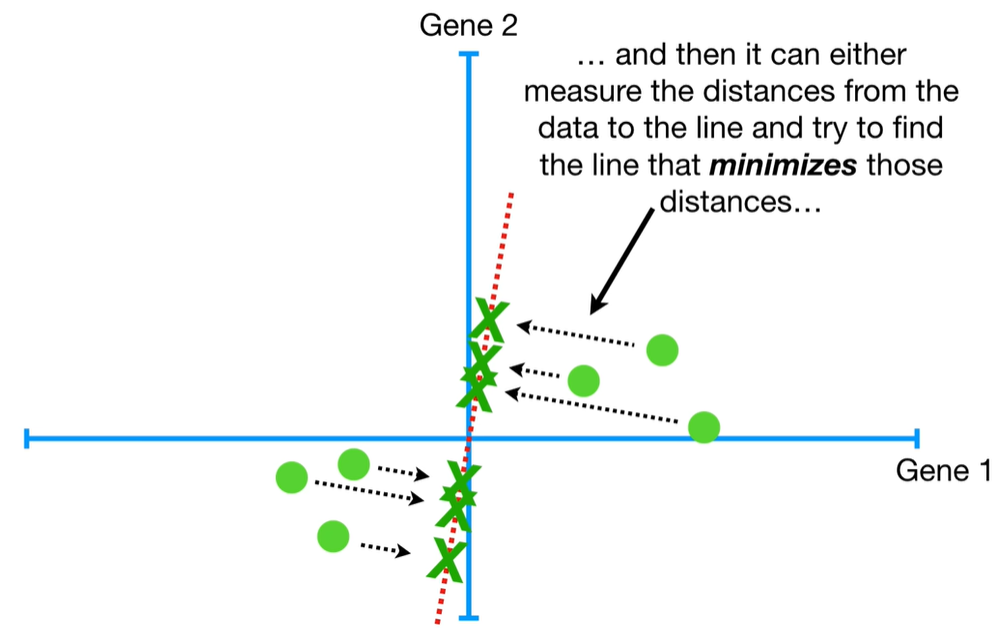
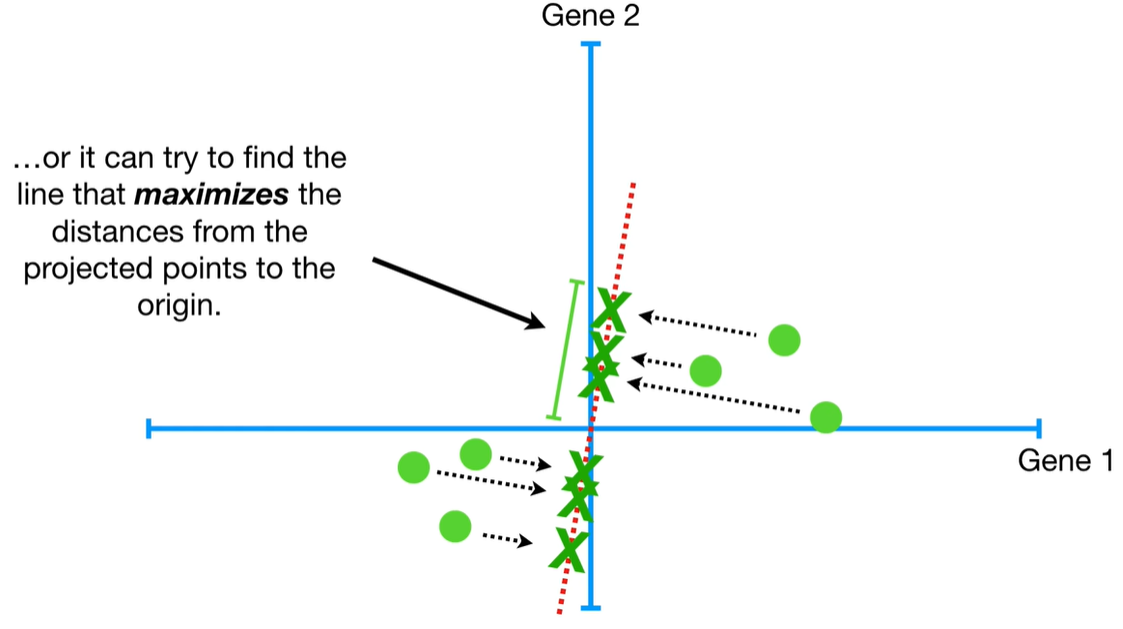
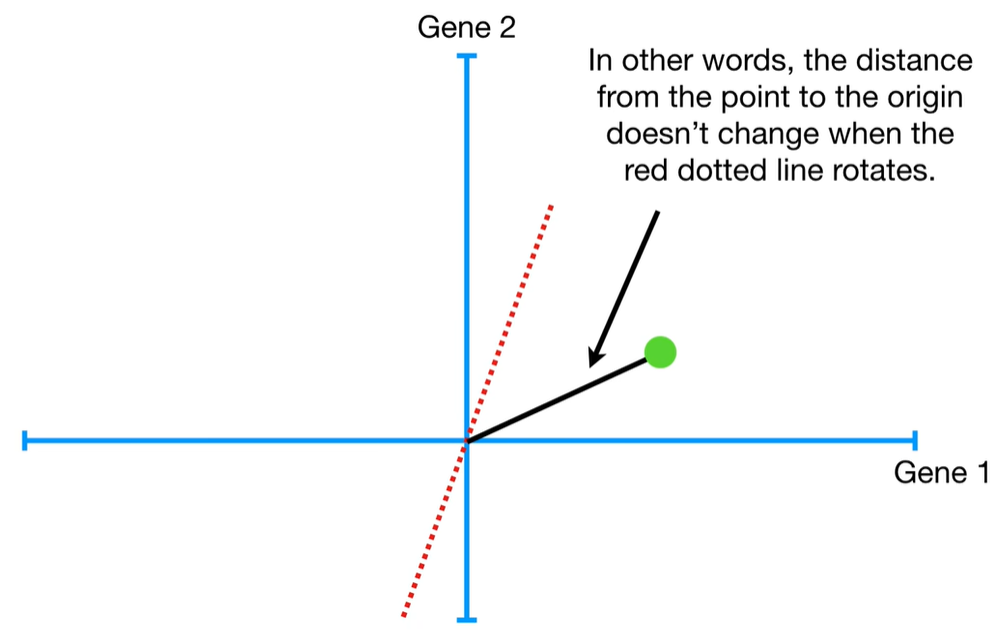
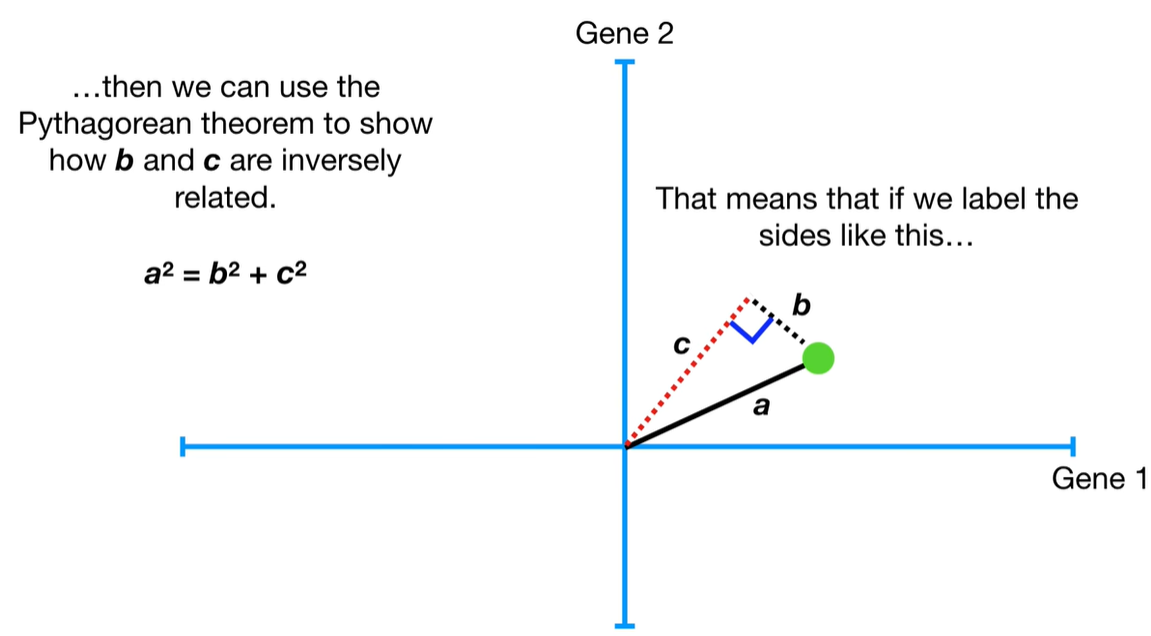
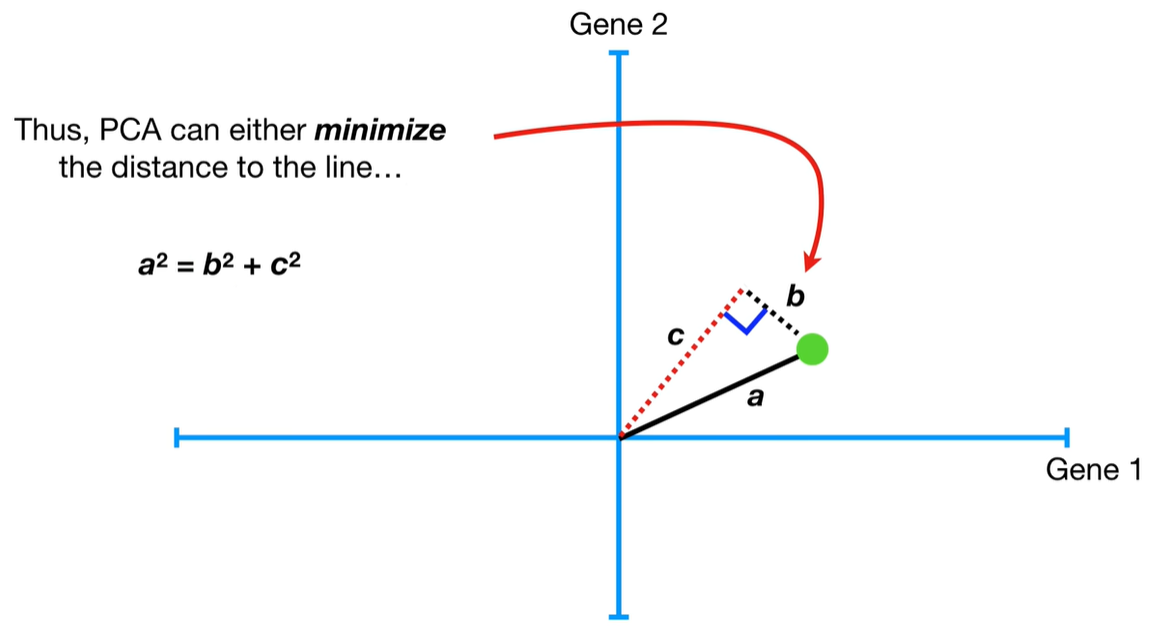
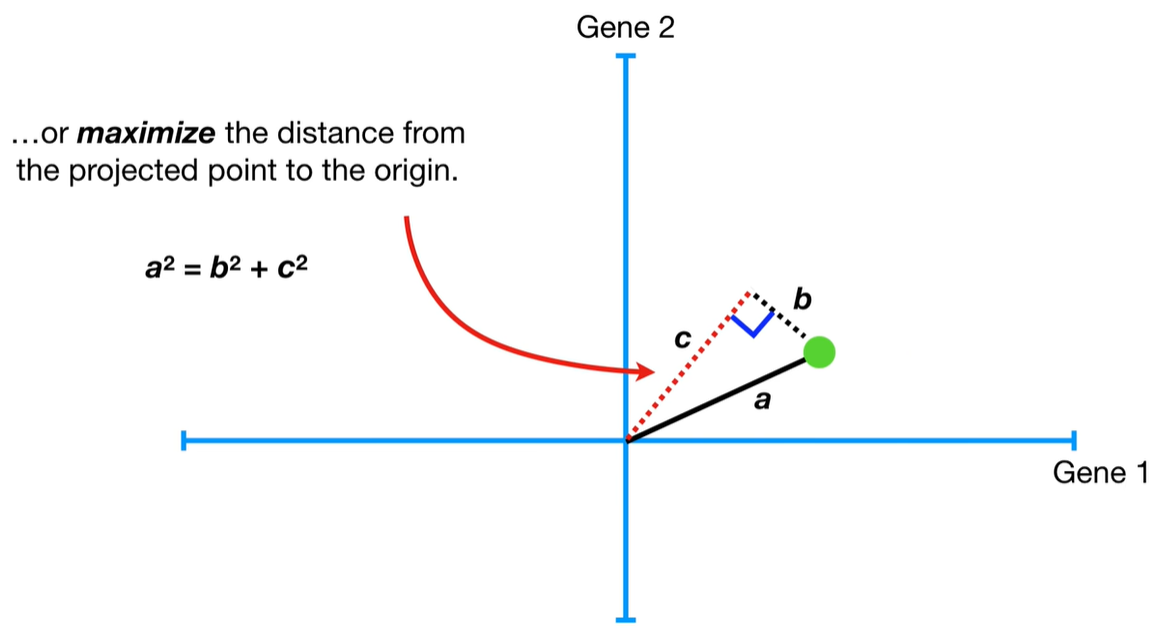
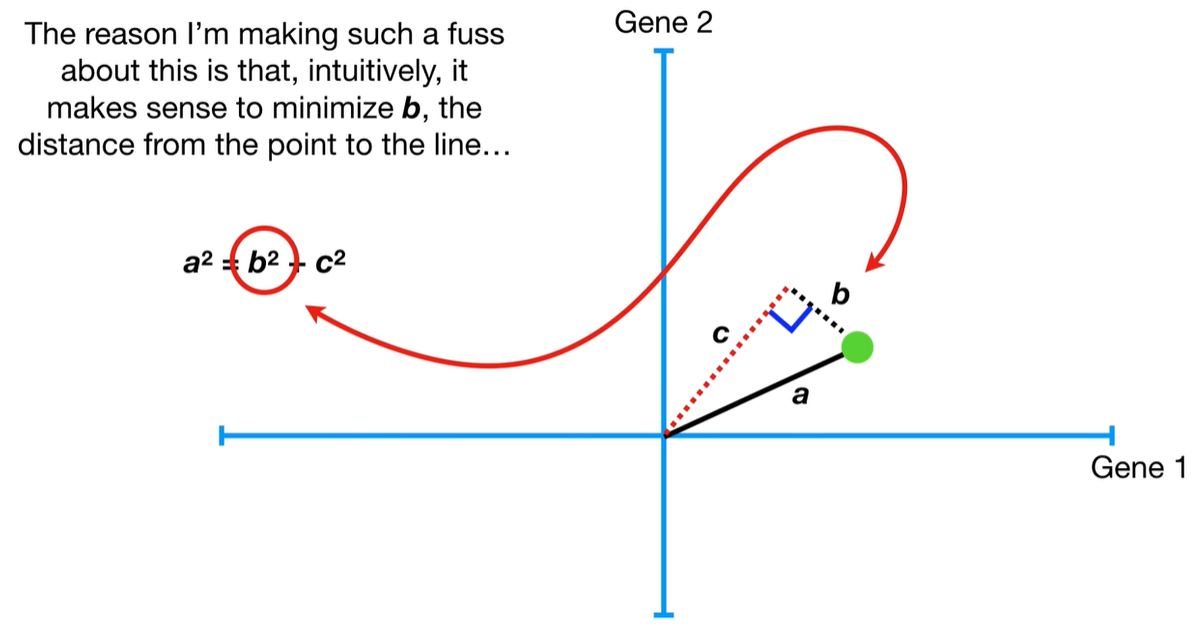
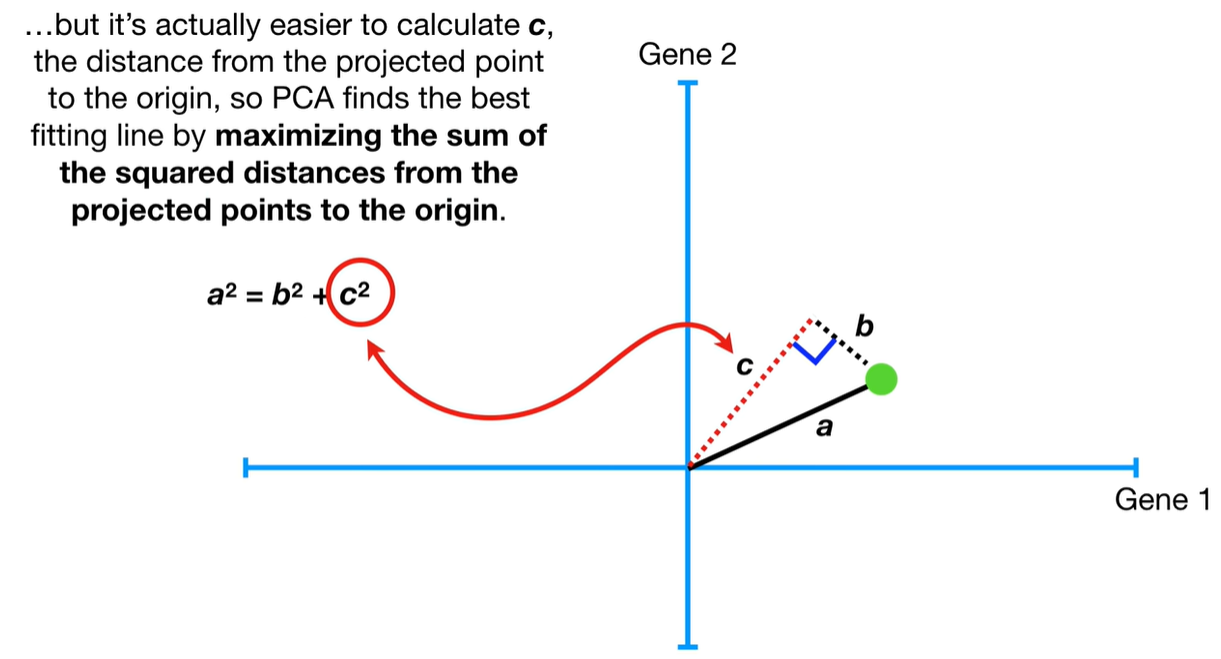
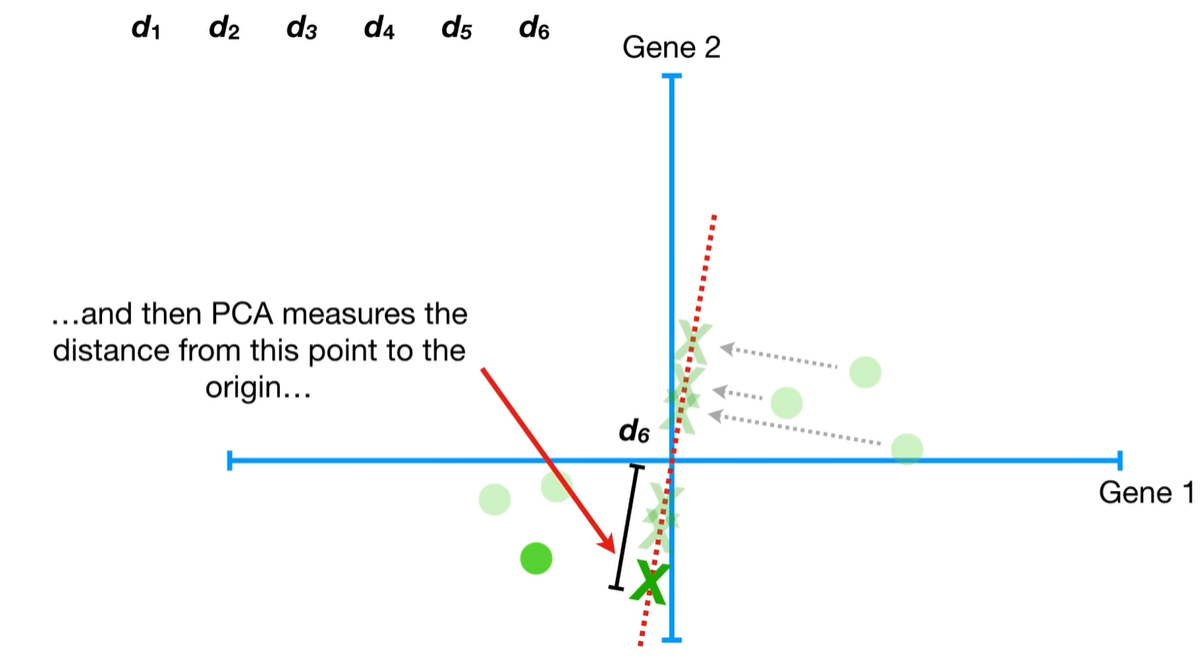
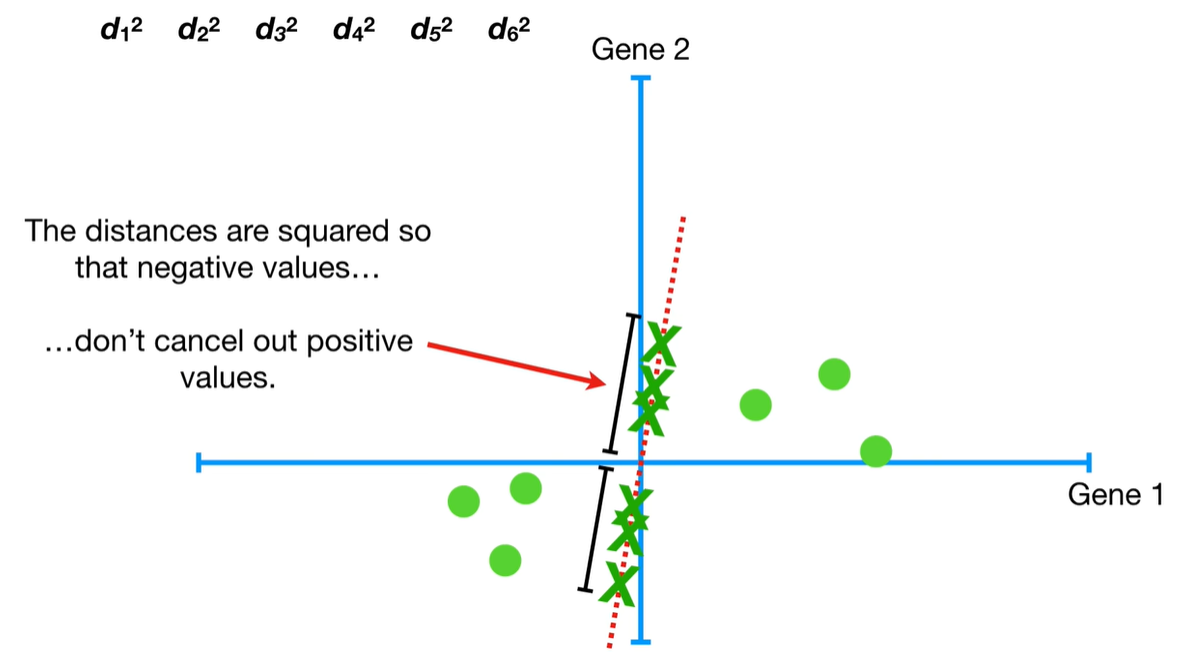
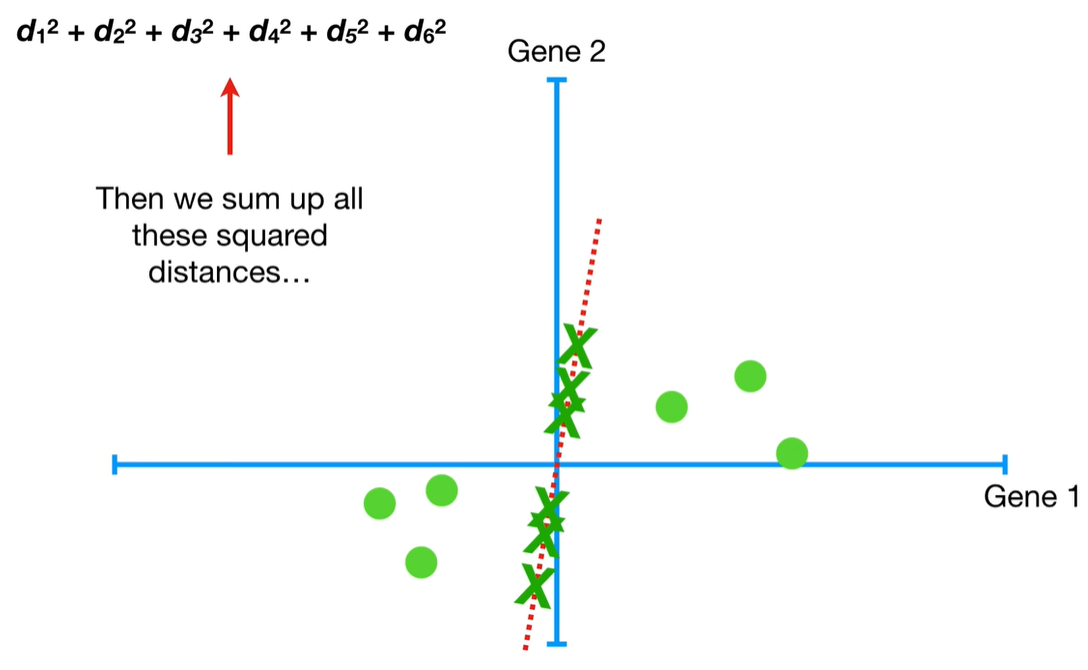

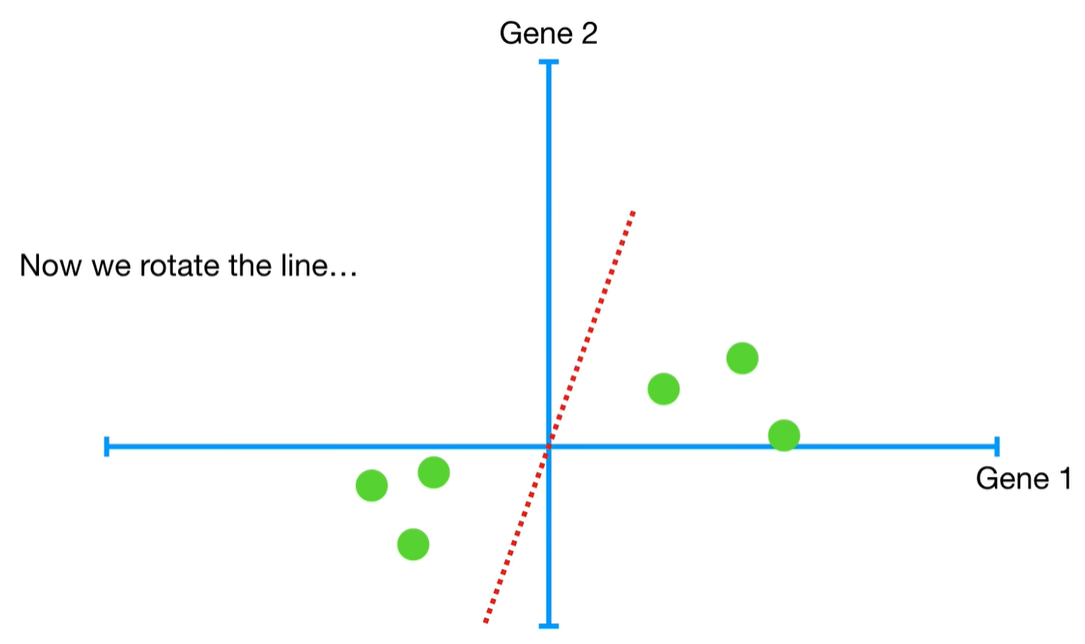

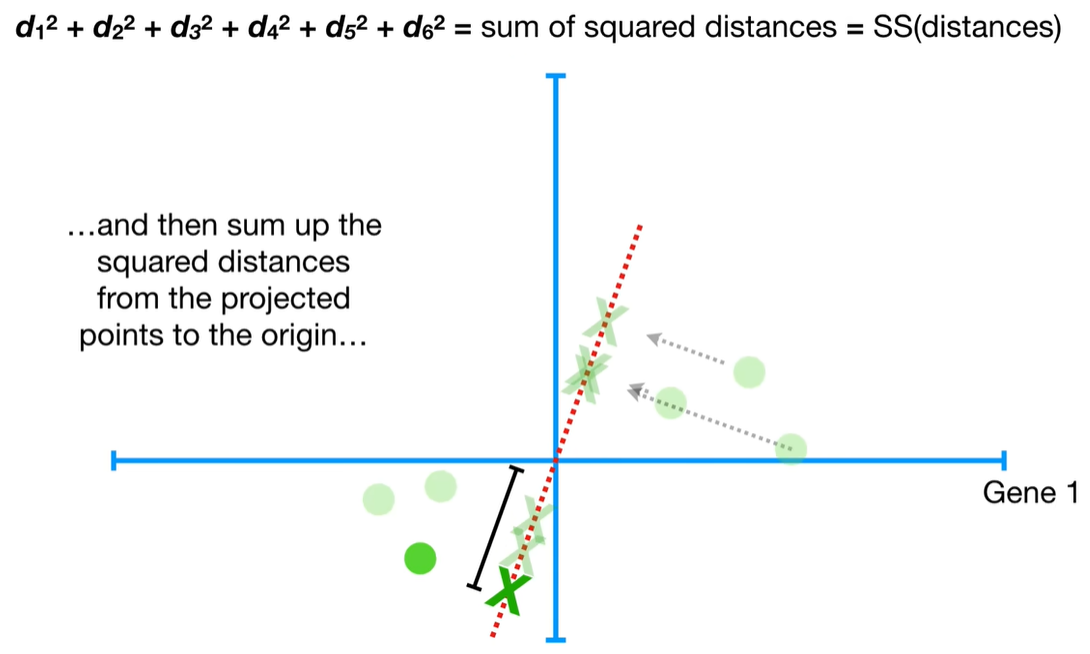
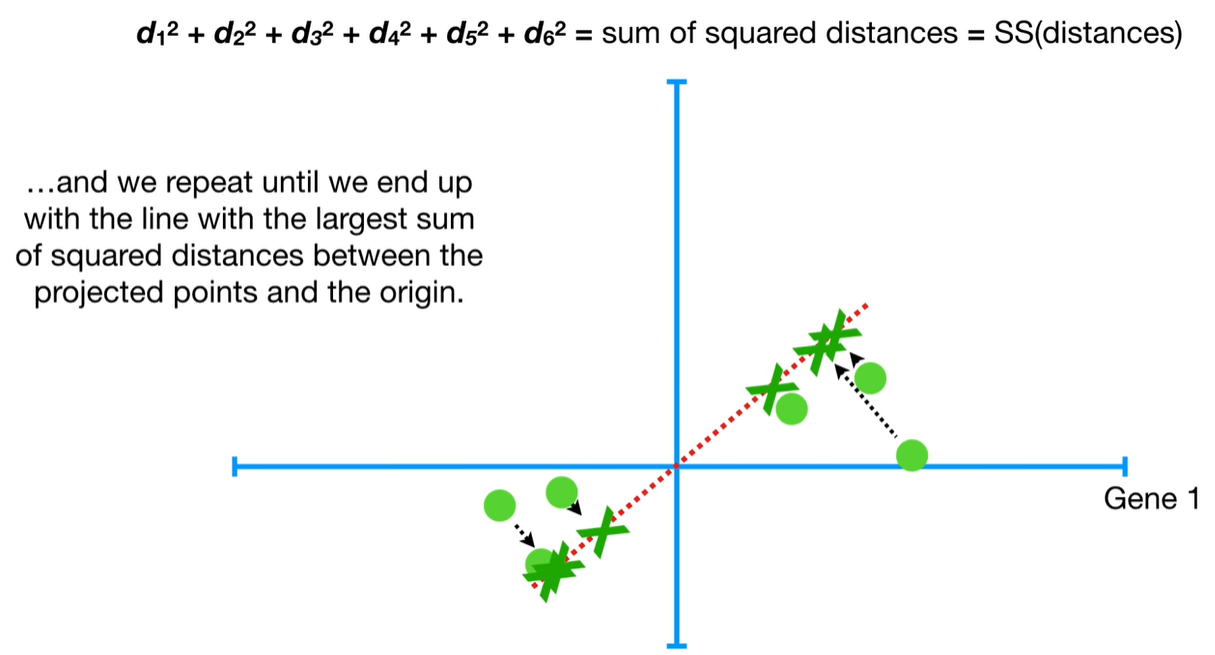
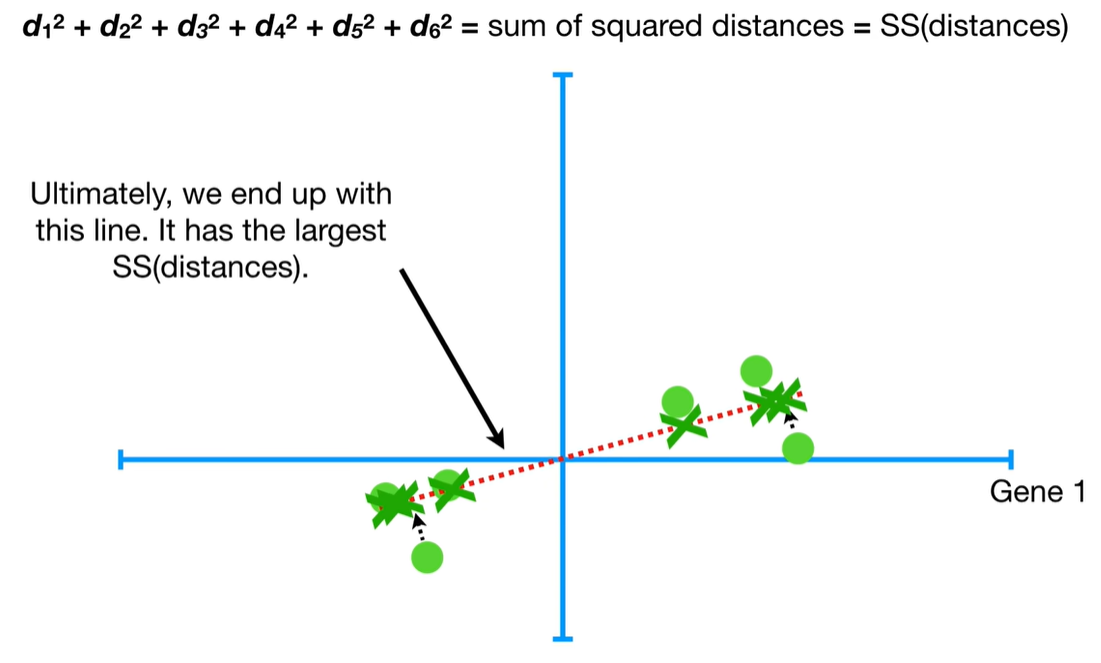
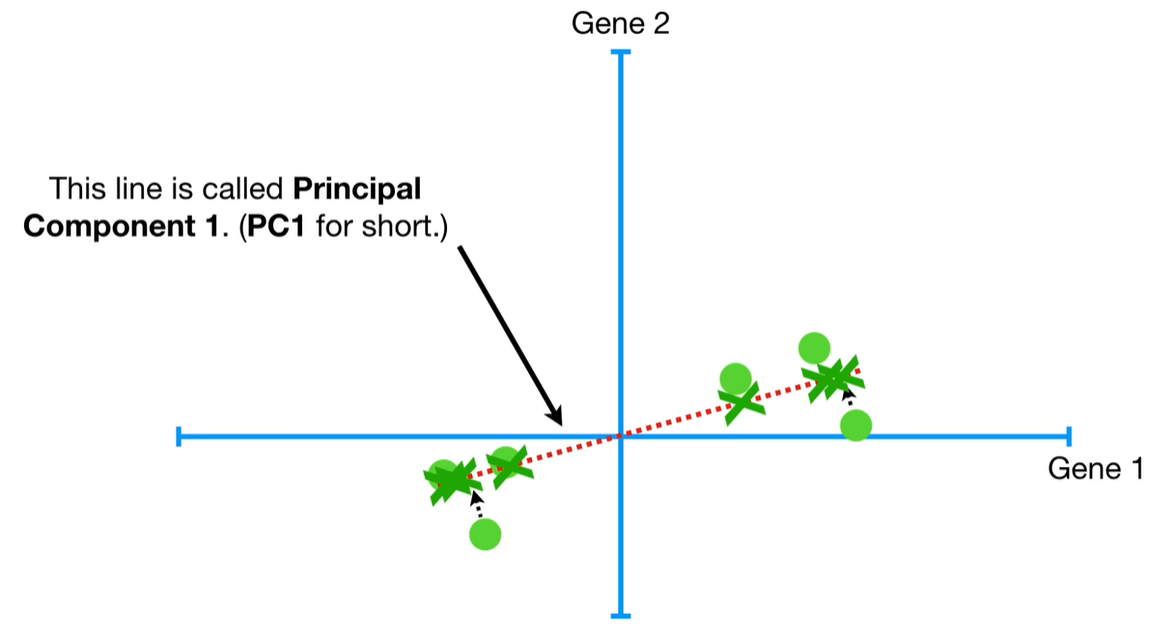

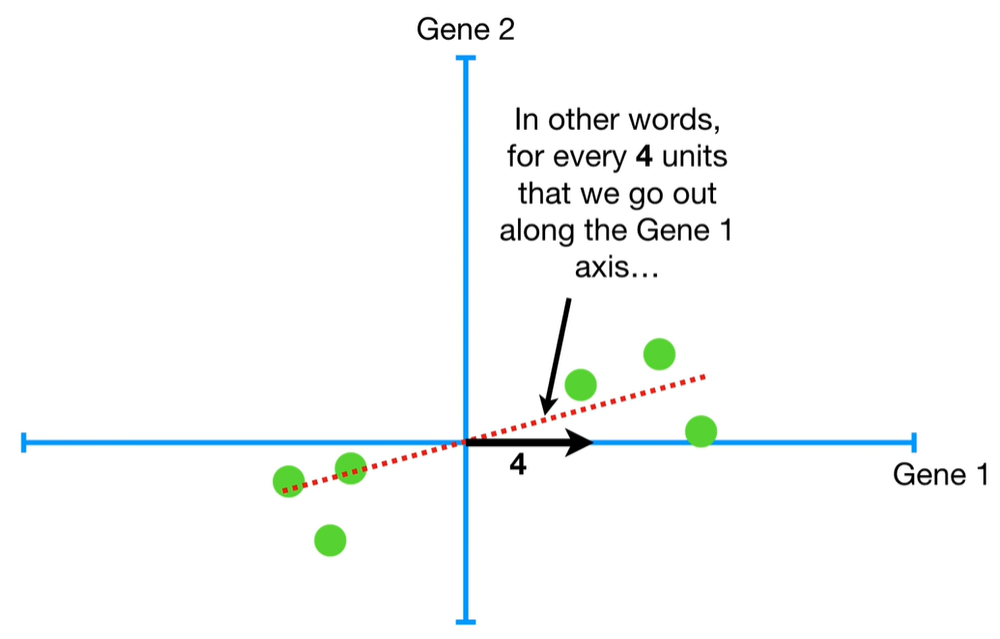
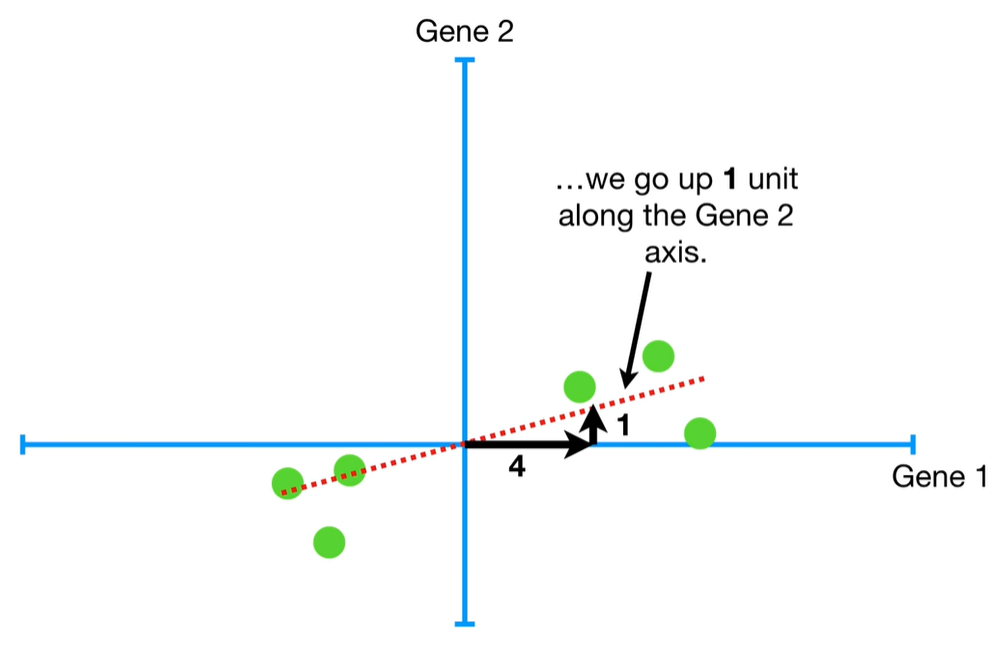
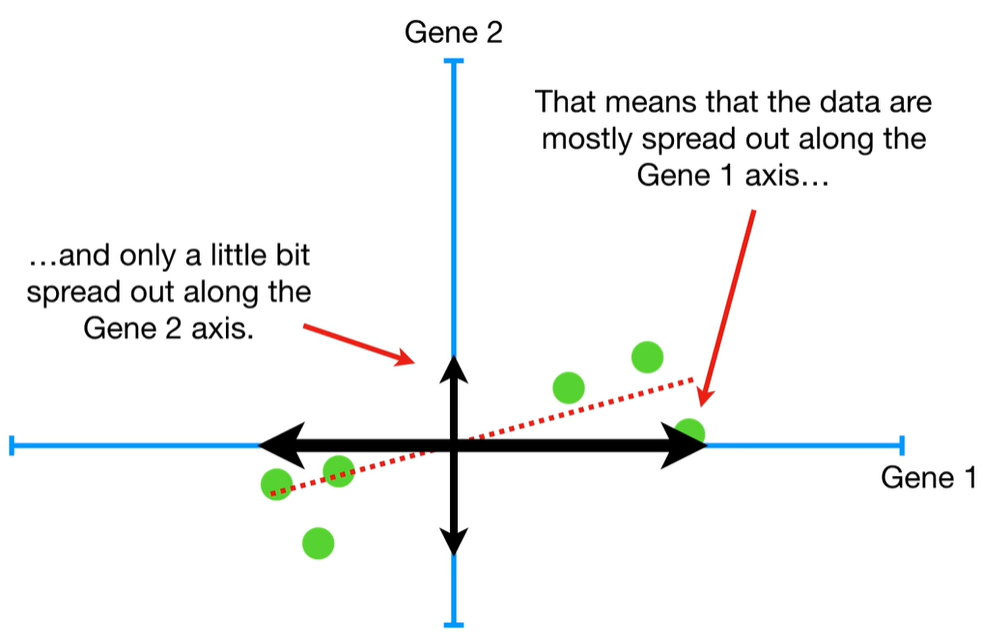
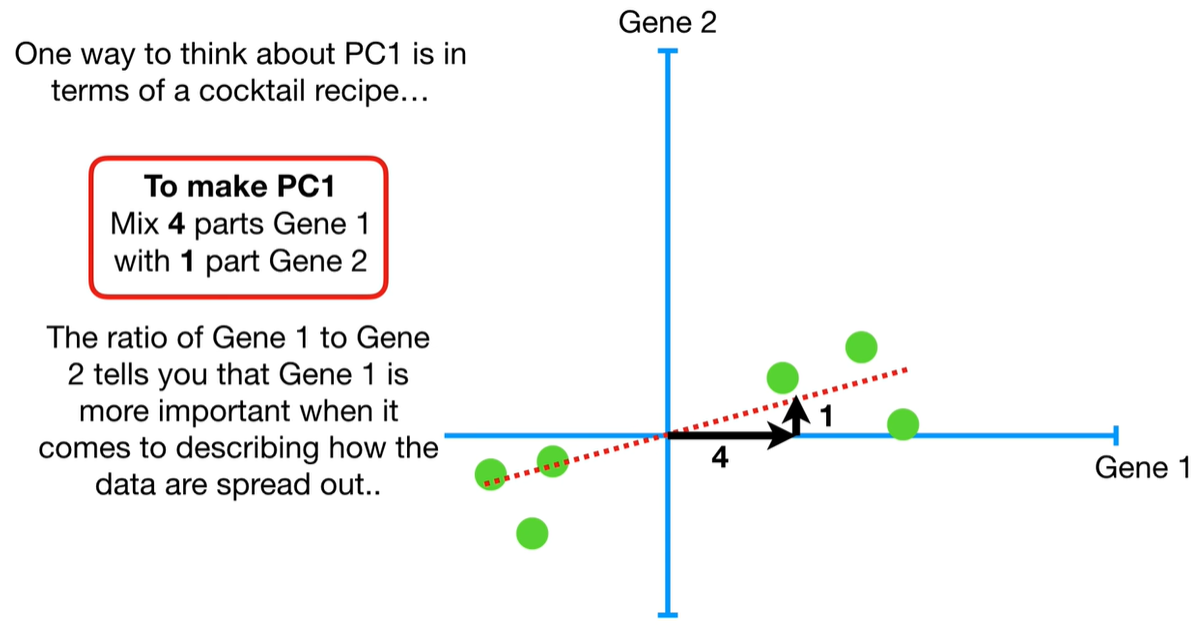

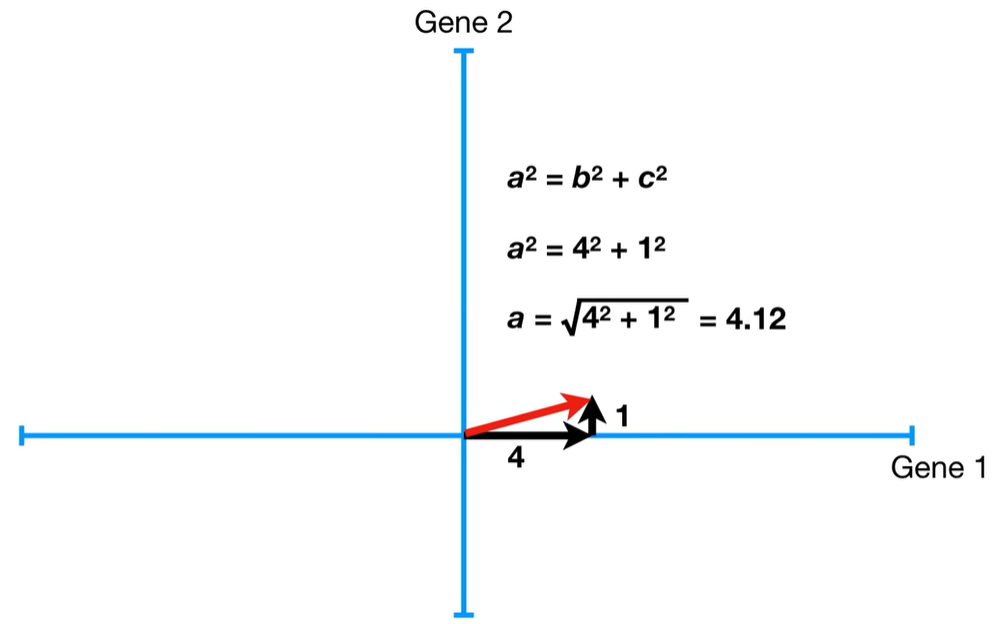
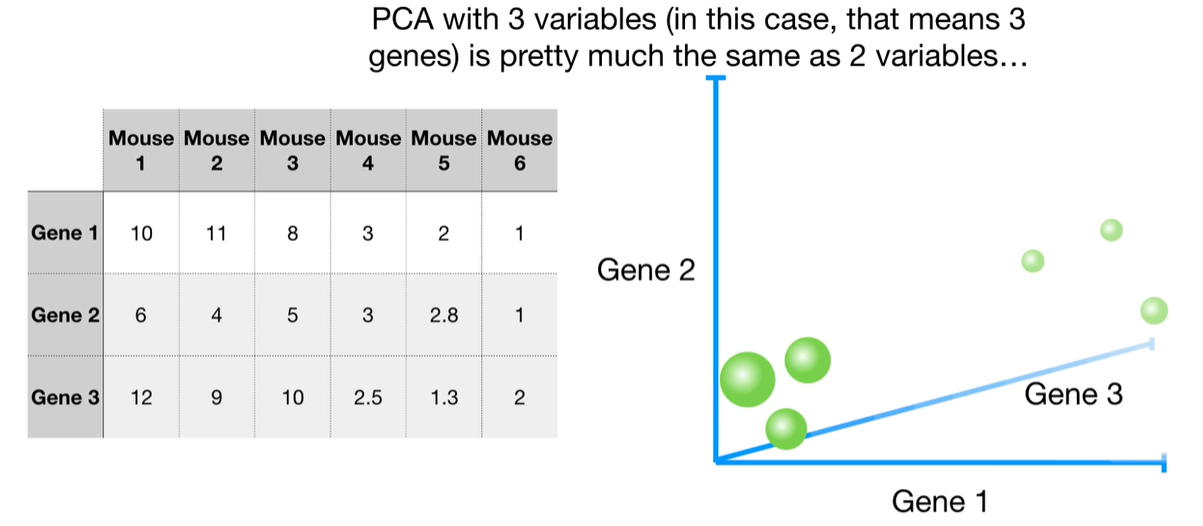
 understand the variables vectors rather than scalers
understand the variables vectors rather than scalers
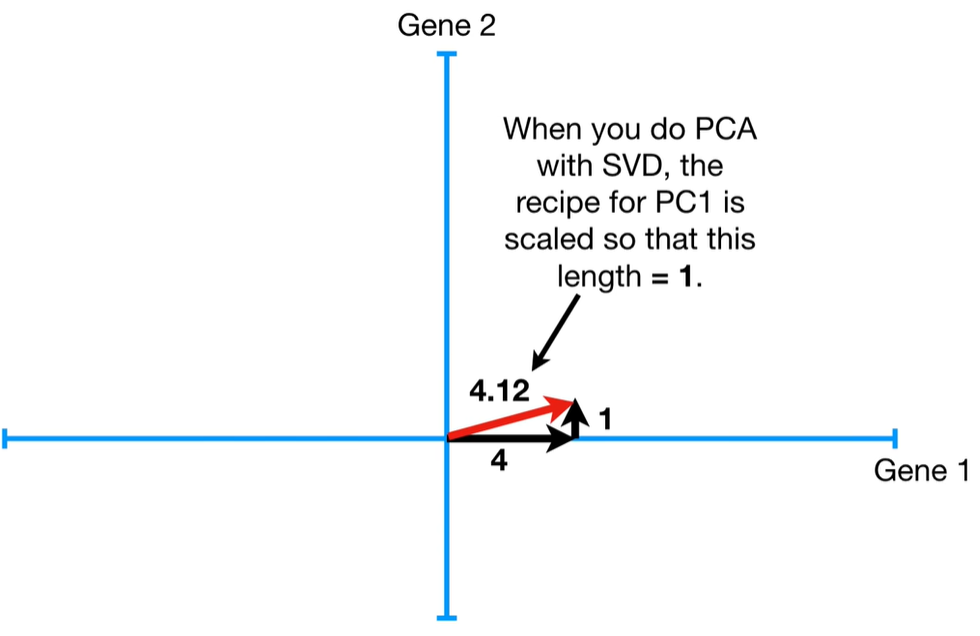
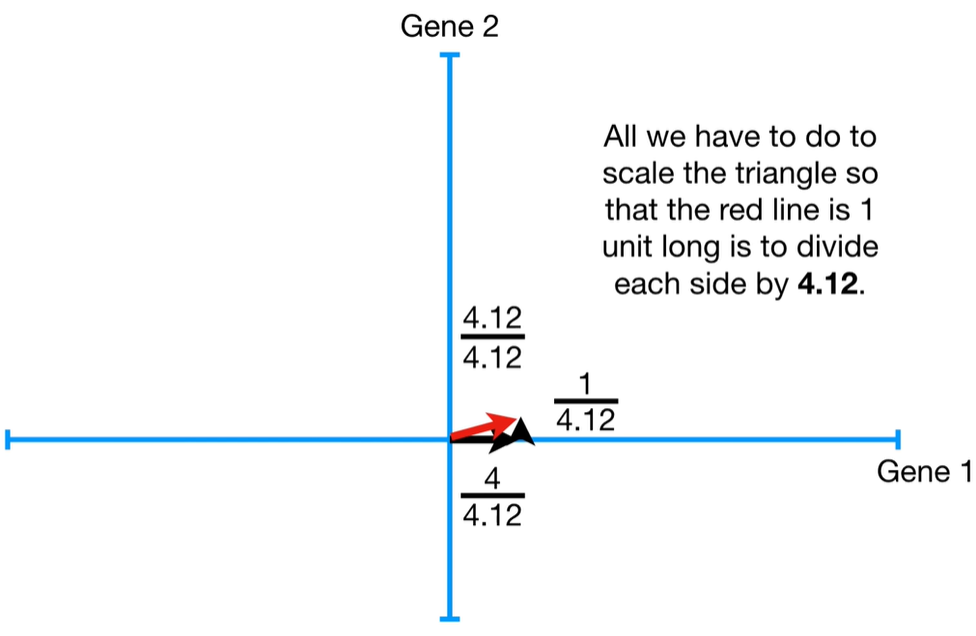
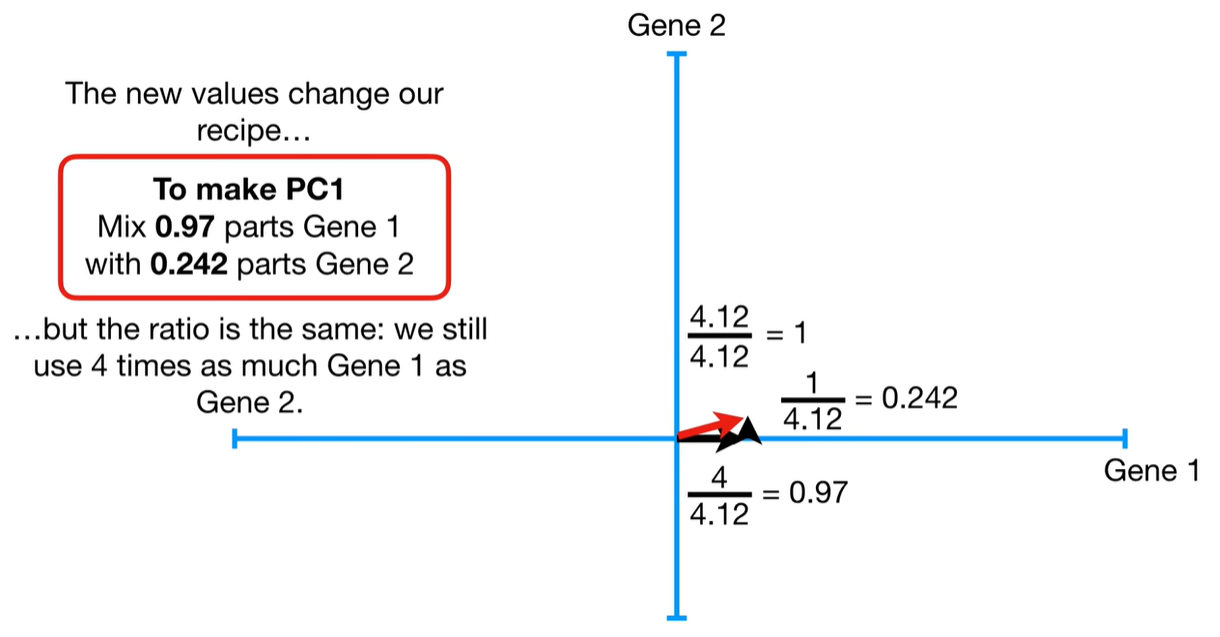
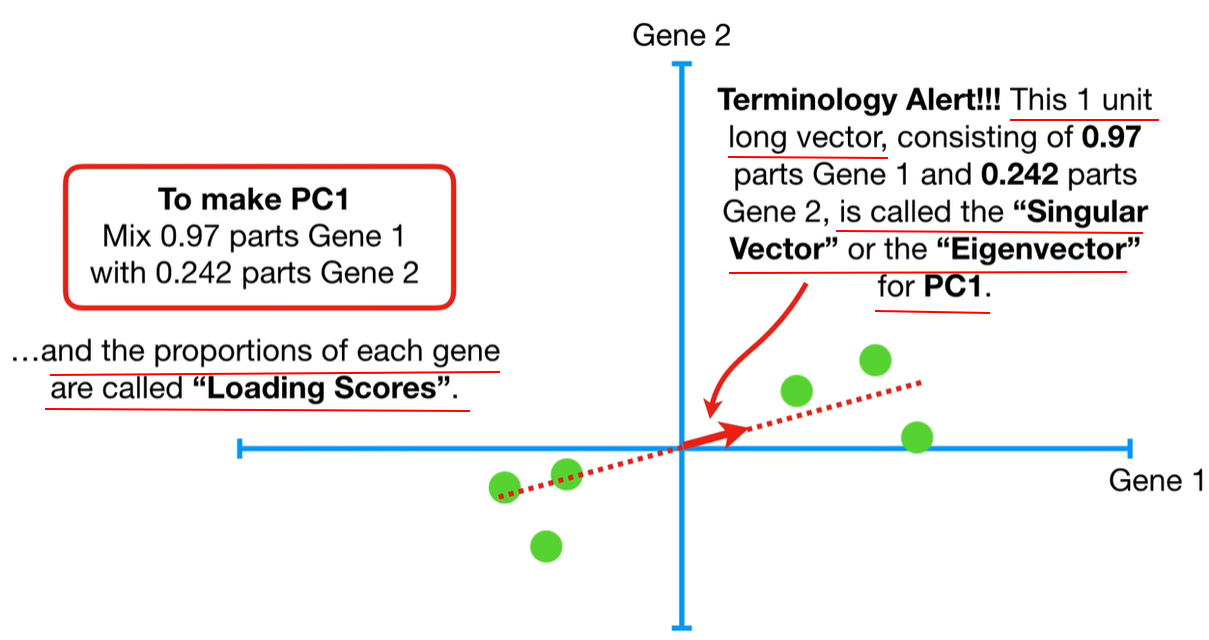
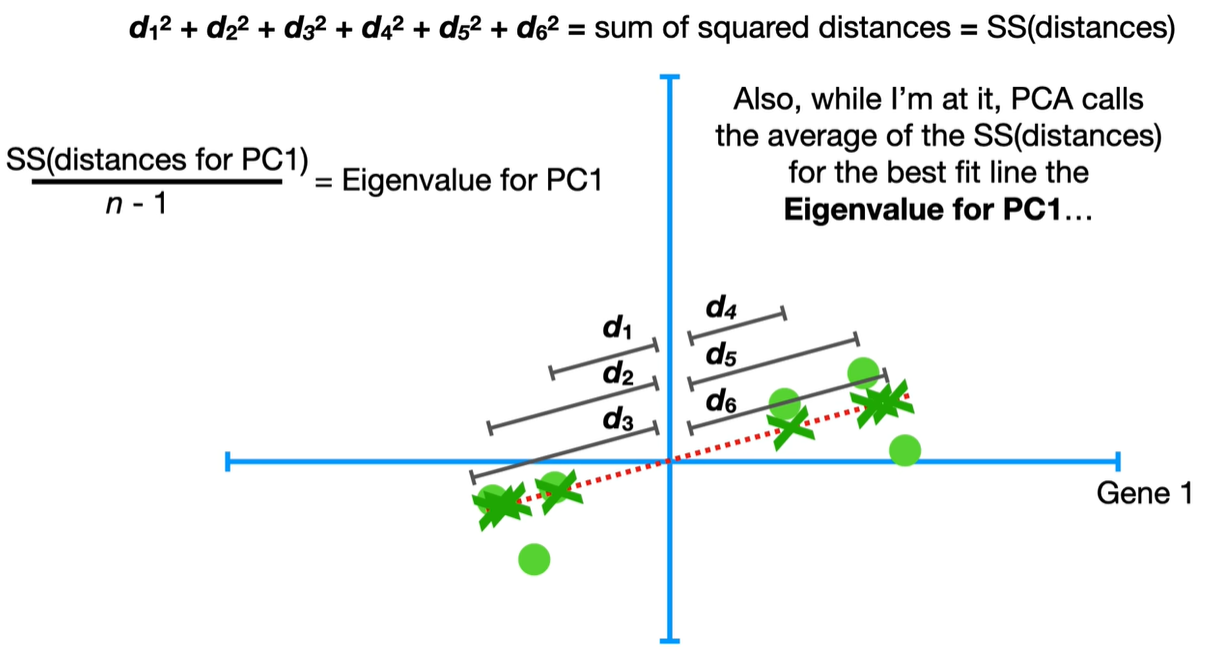
Step-by-step process to calculate eigenvalues in PCA
✅ Step 1: Standardize the data
Before applying PCA, standardize your data to have mean = 0 and standard deviation = 1 for each feature (unless already standardized).

✅ Step 2: Compute the covariance matrix
Let the standardized data matrix be Z (with shape n×p, where n is the number of samples and p the number of features). The covariance matrix is:
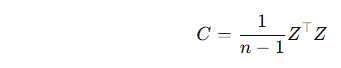
C will be a p×p matrix.
✅ Step 3: Compute eigenvalues and eigenvectors
You now solve the eigenvalue problem for the covariance matrix:

-
λ are the eigenvalues (scalars)
-
v are the eigenvectors (principal components)
The eigenvalues are the solutions to the characteristic equation:
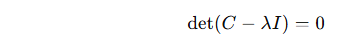
Use numerical methods (e.g. in Python with NumPy) to compute these.
💡 Interpretation
-
Each eigenvalue λi indicates the variance explained by the corresponding principal component.
-
The sum of all eigenvalues equals the total variance in the dataset.
-
Larger eigenvalues → more important principal components.
import numpy as np # Example data (rows = samples, columns = features) X = np.array([[2.5, 2.4], [0.5, 0.7], [2.2, 2.9], [1.9, 2.2], [3.1, 3.0]]) # Step 1: Standardize the data X_centered = X - np.mean(X, axis=0) # Step 2: Covariance matrix cov_matrix = np.cov(X_centered, rowvar=False) # Step 3: Eigenvalues and eigenvectors eigenvalues, eigenvectors = np.linalg.eig(cov_matrix) print("Eigenvalues:", eigenvalues)
The reason we divide by n−1n - 1n−1 instead of nnn in Step 2 (when computing the covariance matrix in PCA) is because we're computing the sample covariance matrix, not the population covariance matrix.
🔍 Here's the key difference:
-
Divide by nnn → for population covariance (when you have all possible data points).
-
Divide by n−1n - 1n−1 → for sample covariance (when you're working with a sample drawn from a larger population).
📌 Why divide by n−1n - 1n−1 for samples?
This adjustment is known as Bessel’s correction, and it's used to make the sample variance (and hence the sample covariance) an unbiased estimator of the true population variance/covariance.
Without Bessel's correction:

This tends to underestimate the true covariance.
With Bessel's correction:
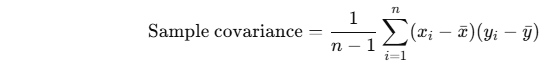
This is unbiased, meaning the expected value of the sample covariance equals the true population covariance.
🧠 In PCA:
Since PCA is usually applied to a sample dataset (not the entire population), we use:
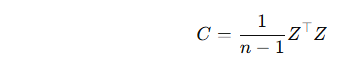
This ensures that the eigenvalues correctly reflect the variance structure of the sample data.


 rotating 90 degree means multiplying i: (4+i)*i = -1+4i
rotating 90 degree means multiplying i: (4+i)*i = -1+4i

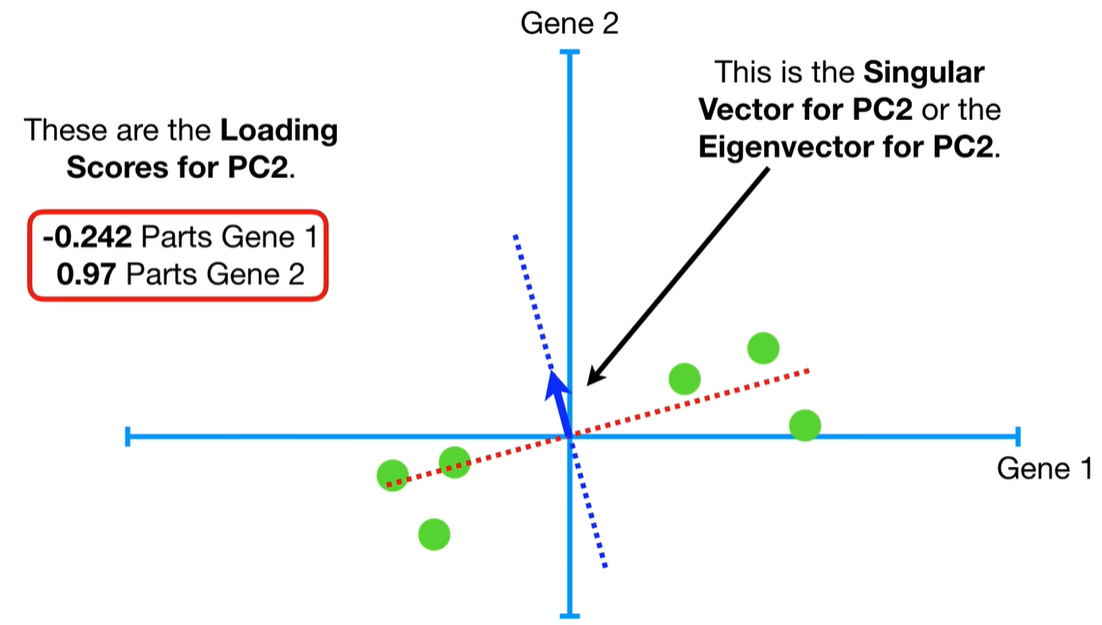
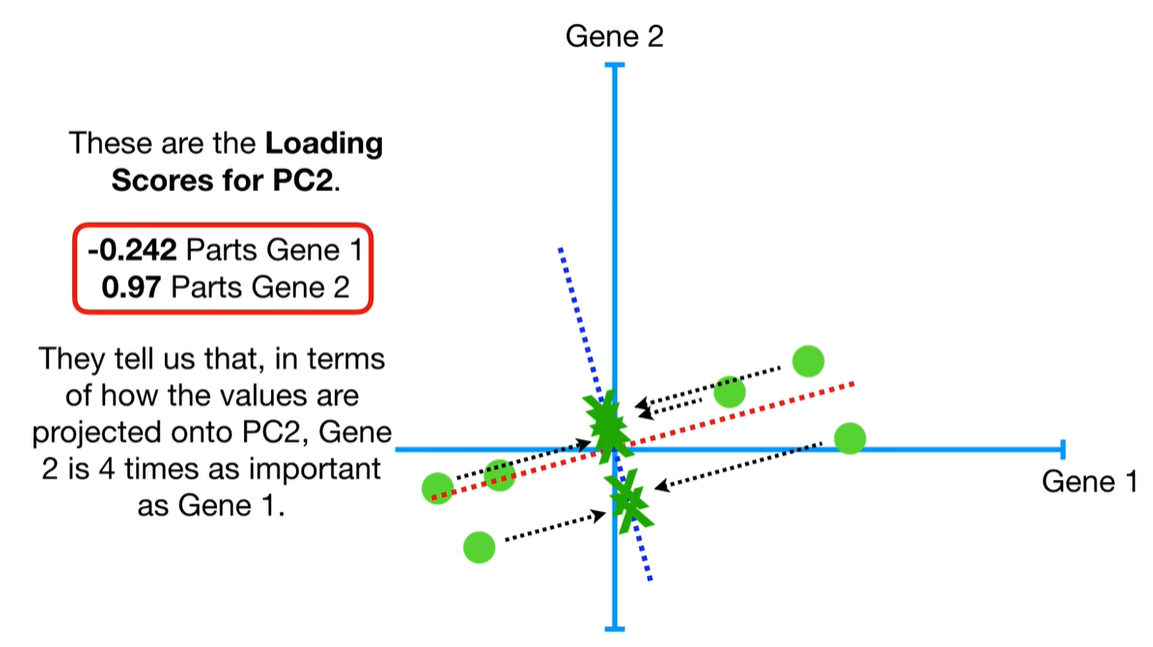

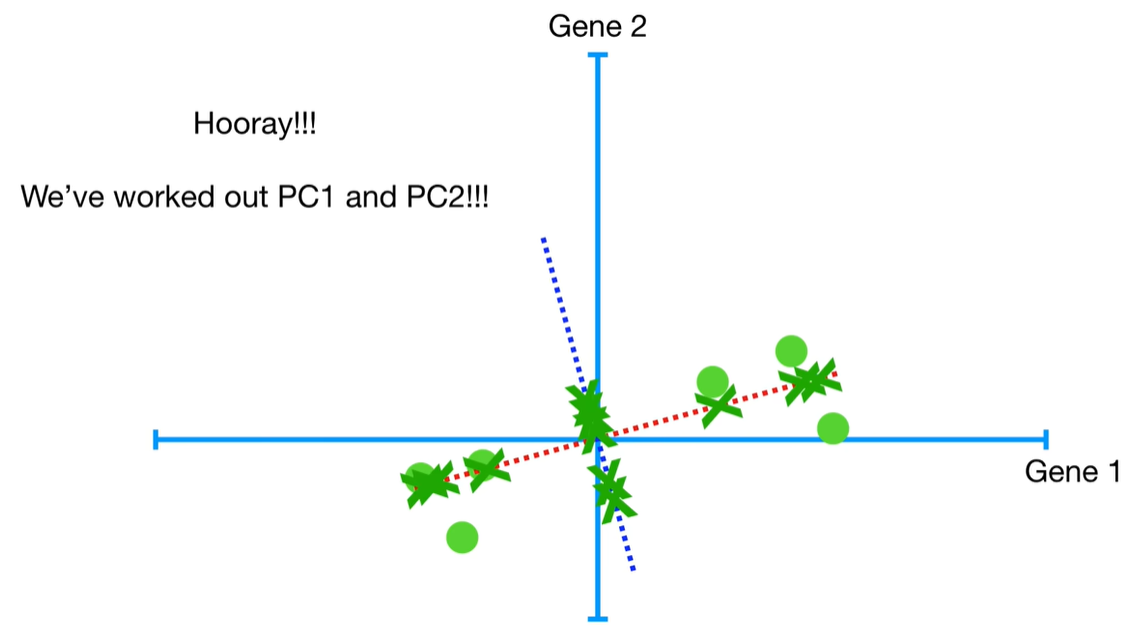
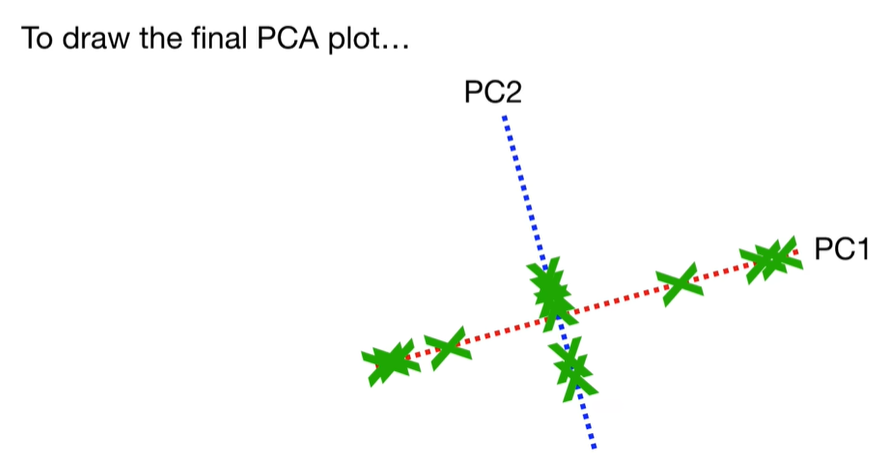
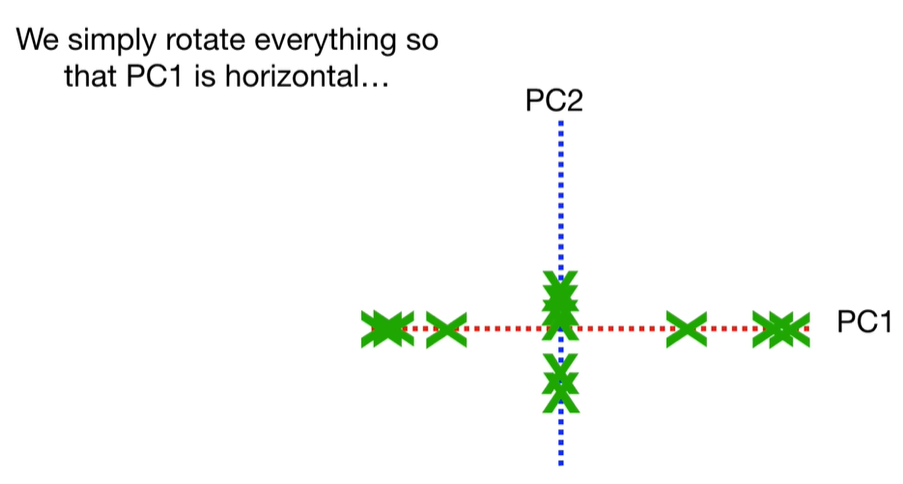

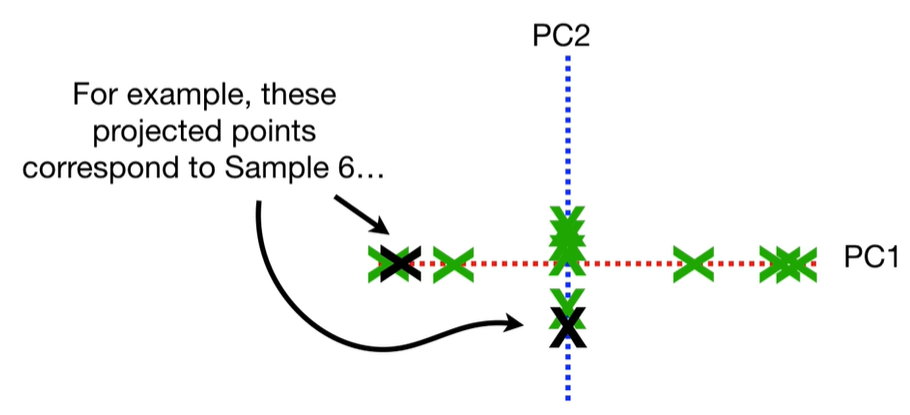
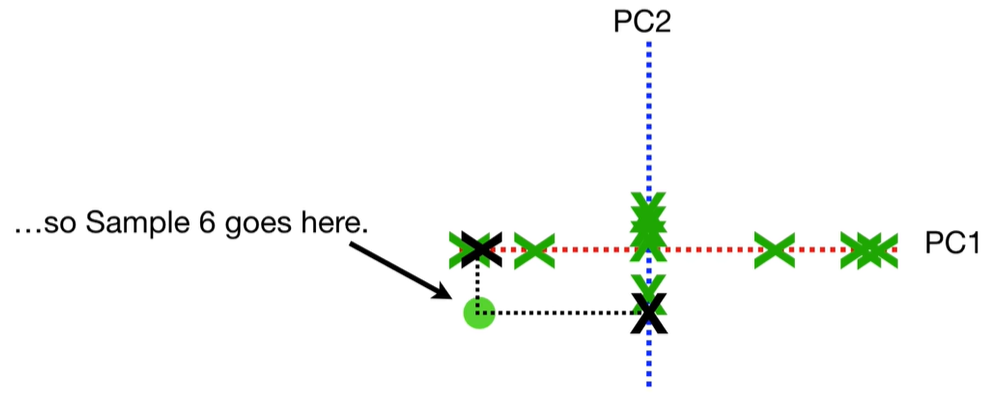
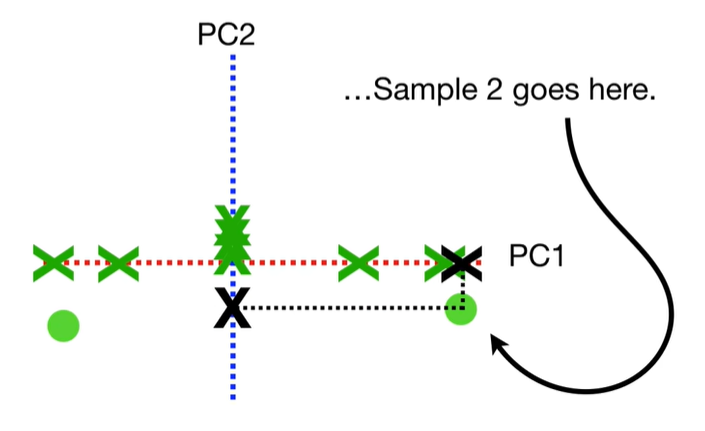

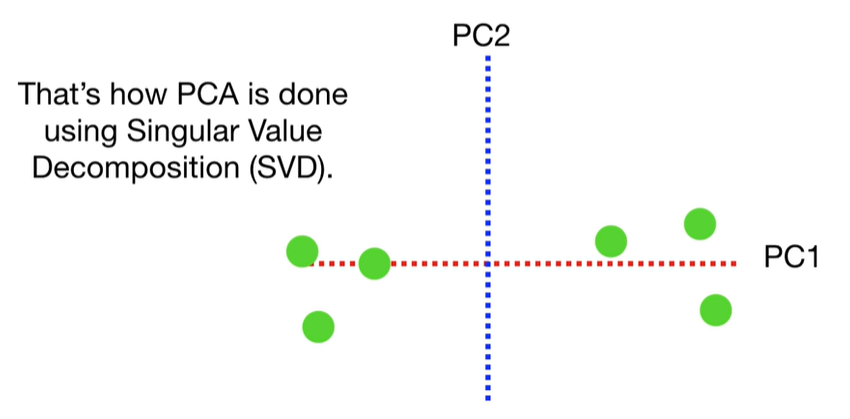

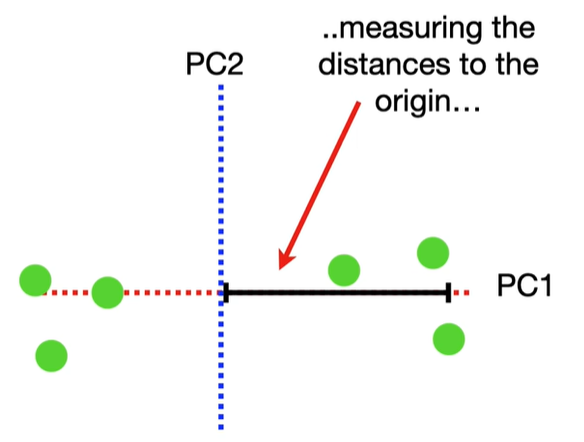
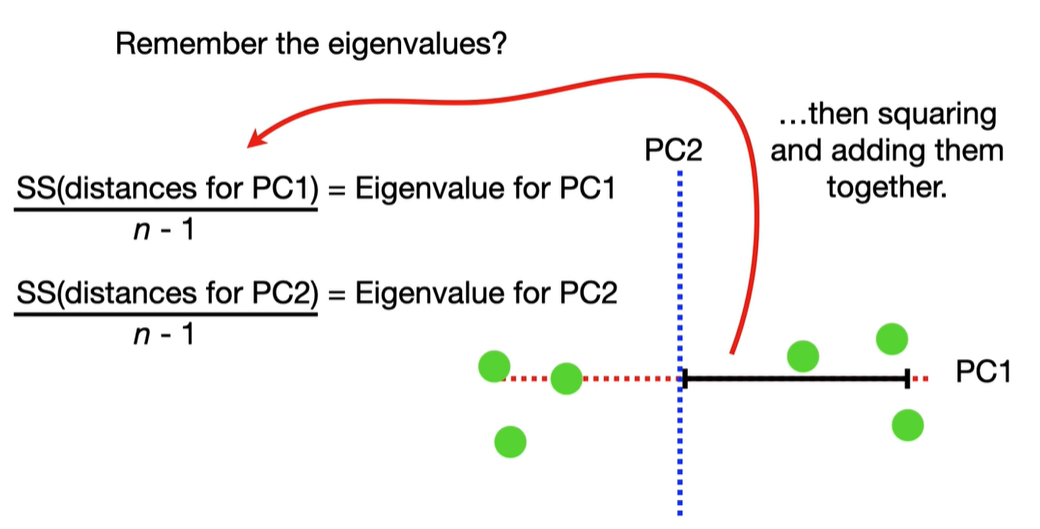

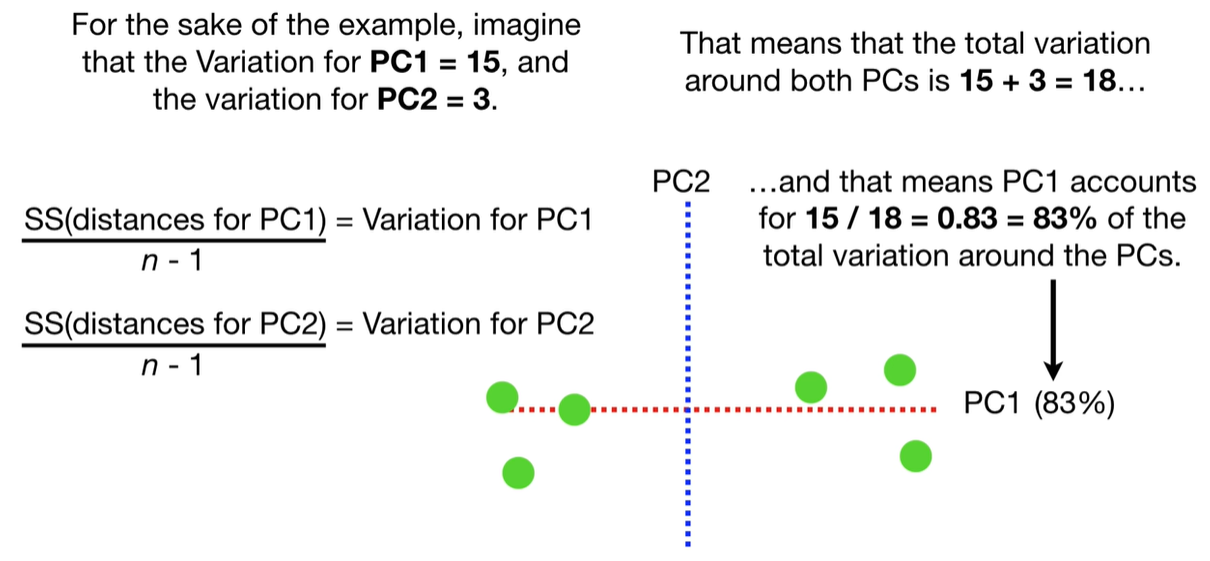
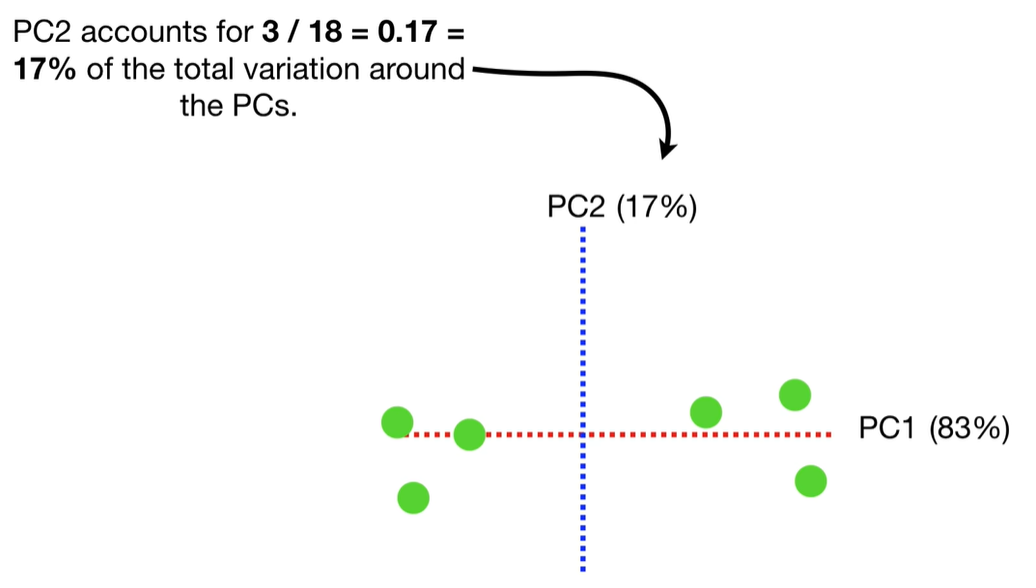
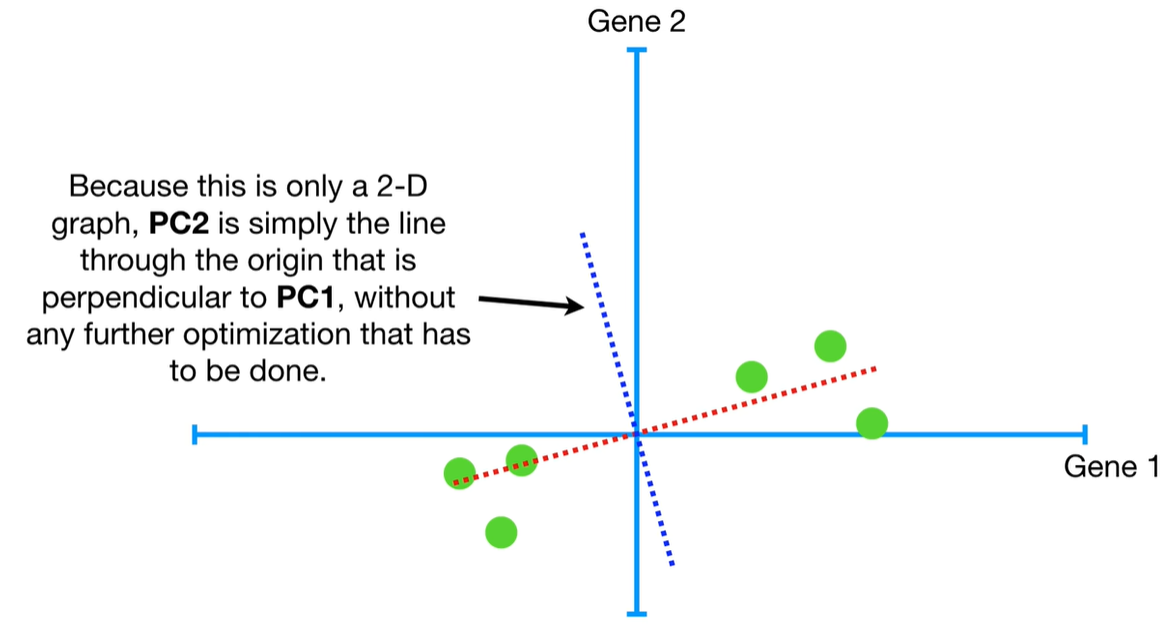
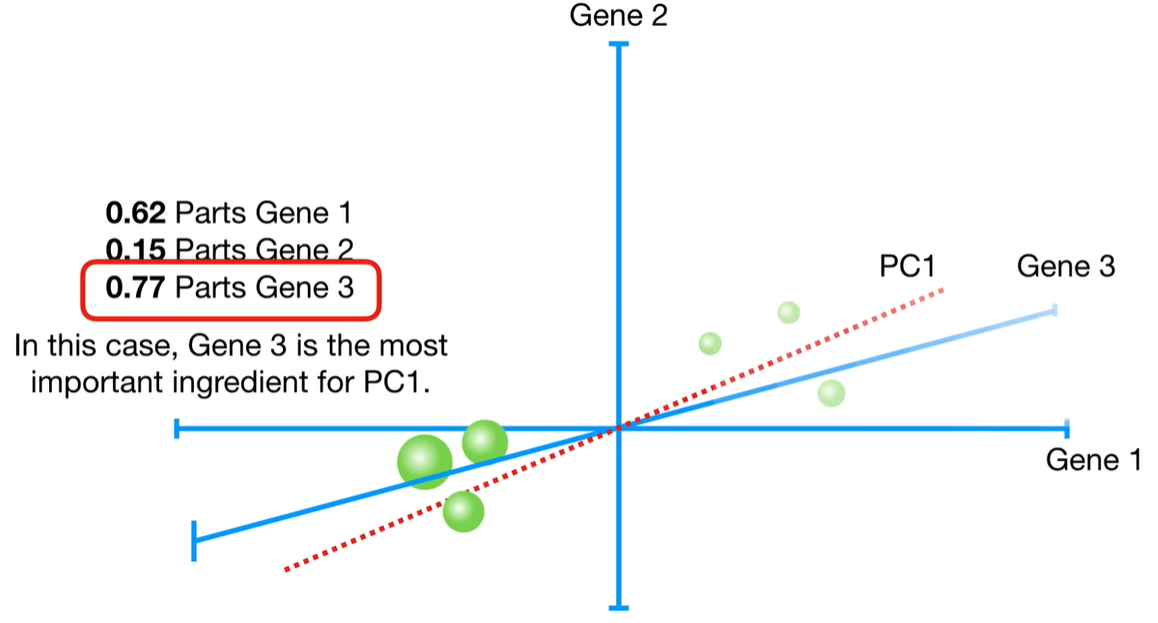
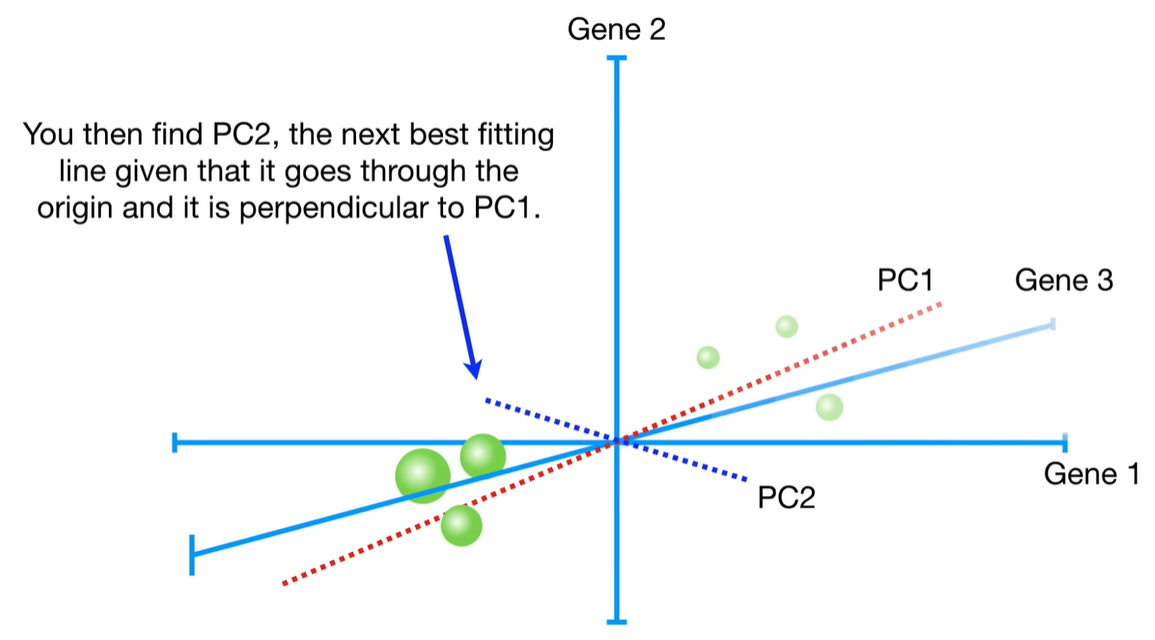
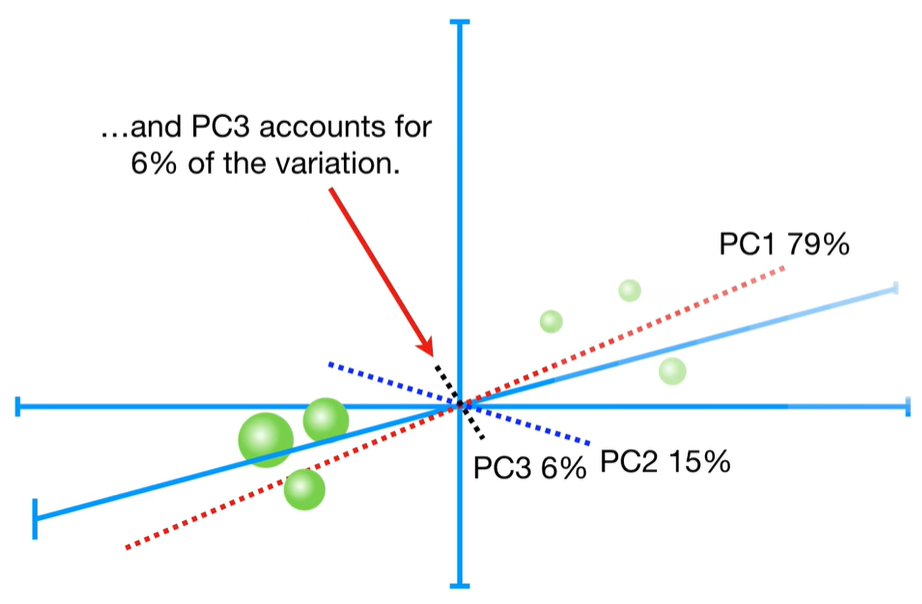
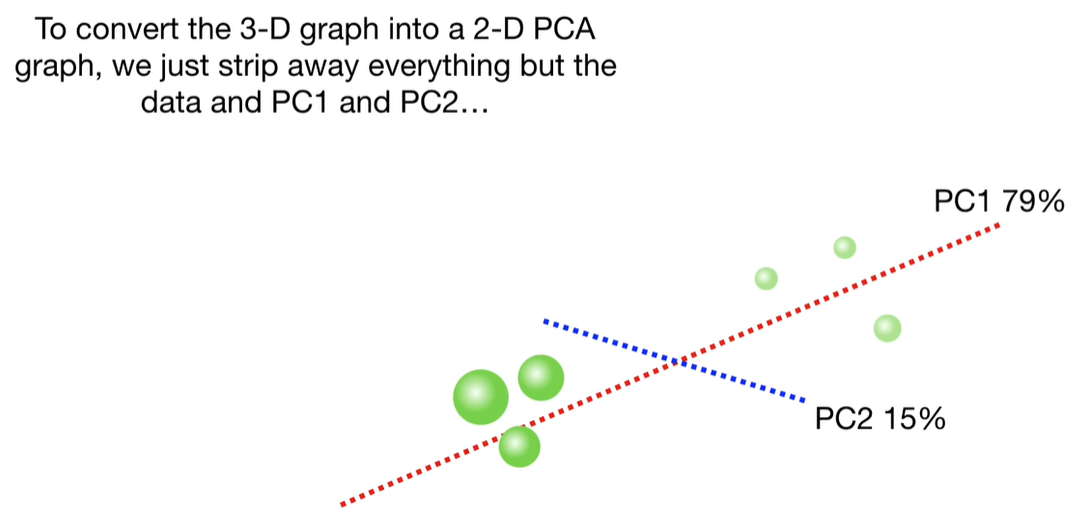
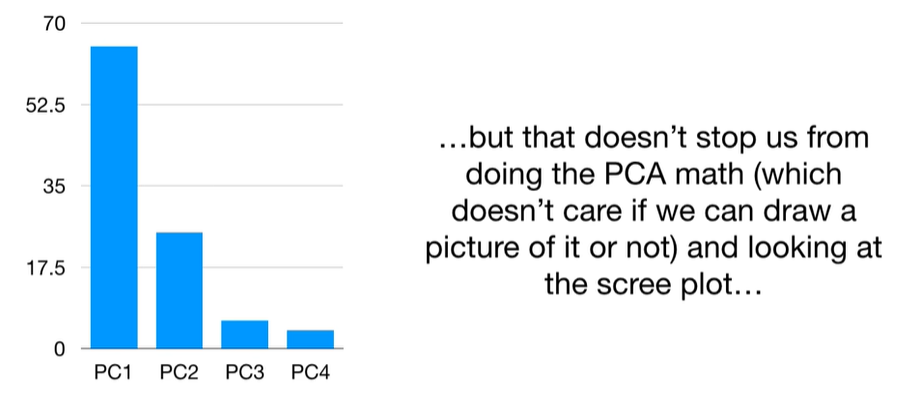
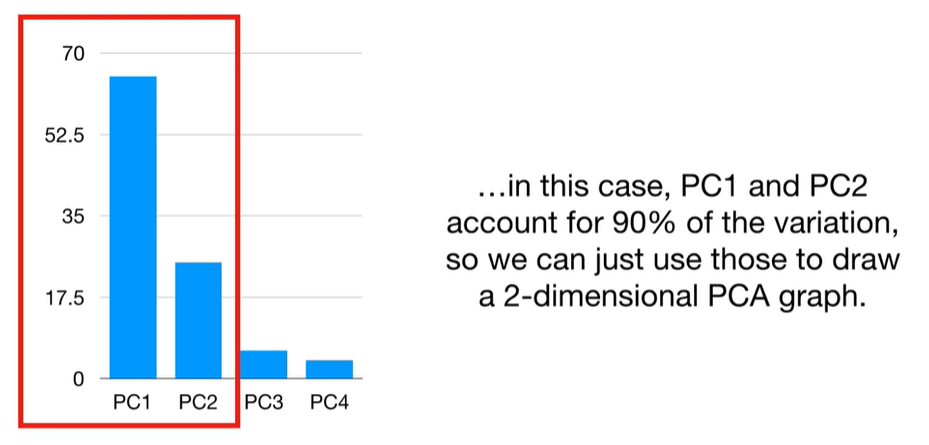
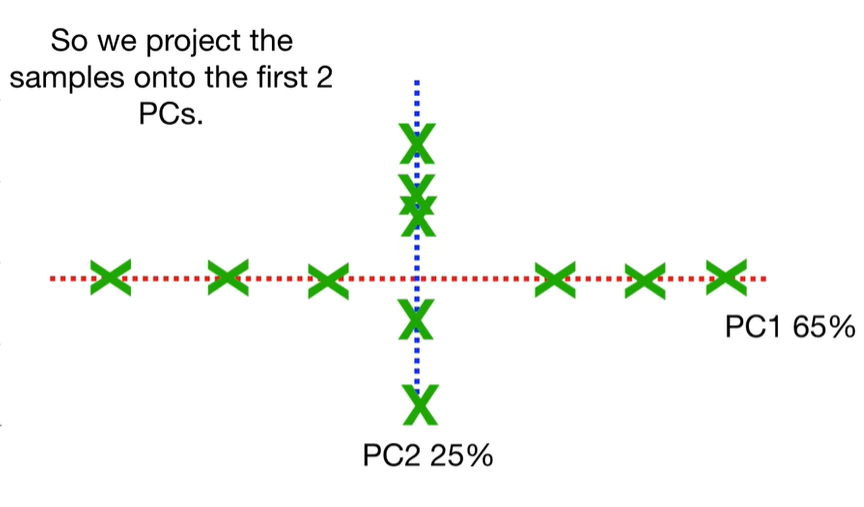
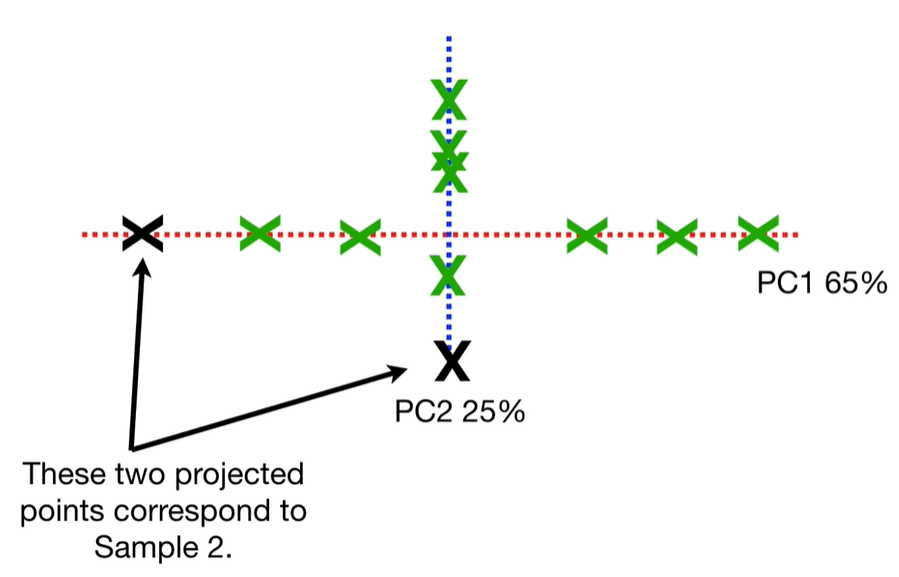
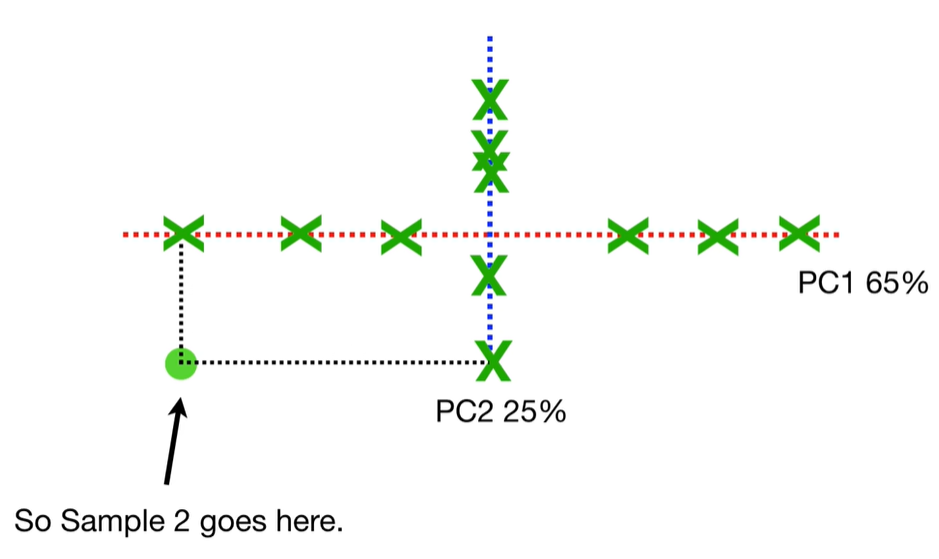
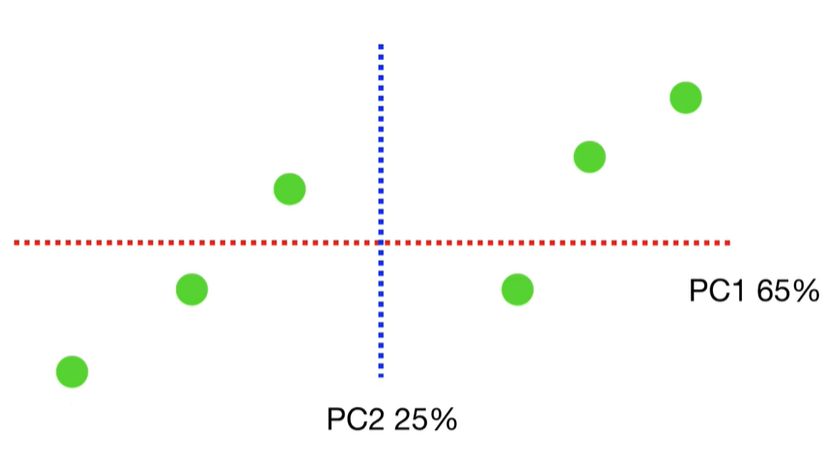
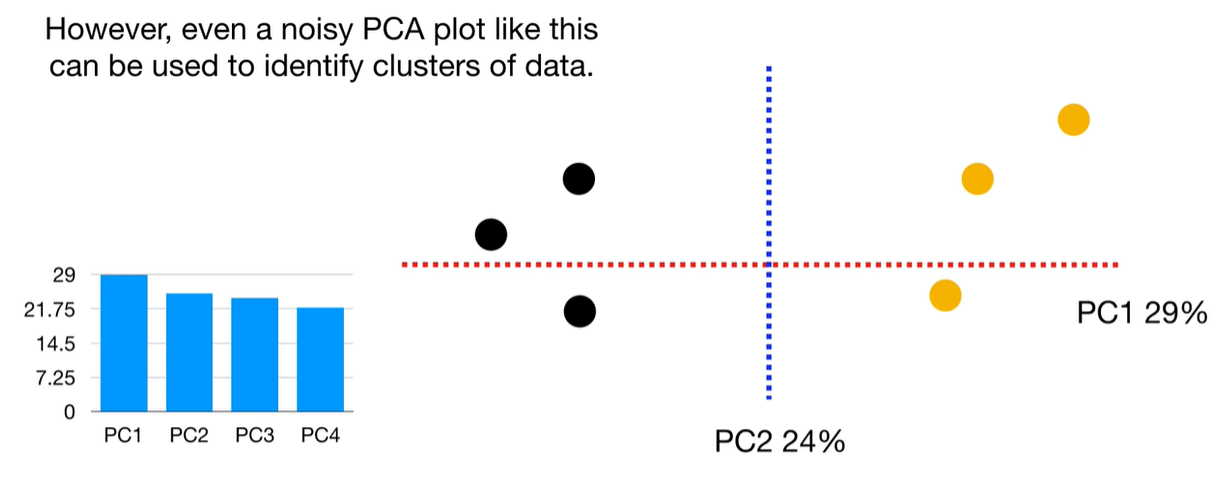
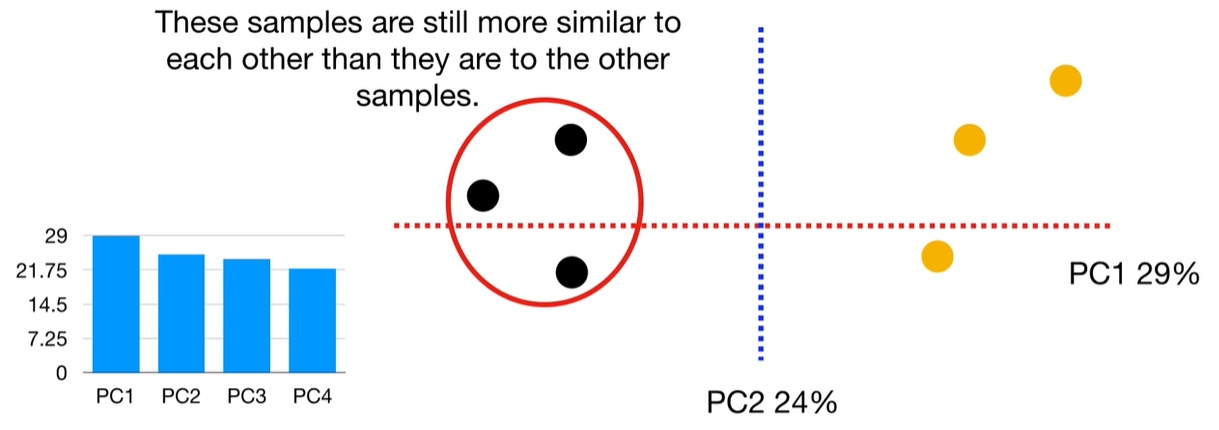
 scree plot
scree plot
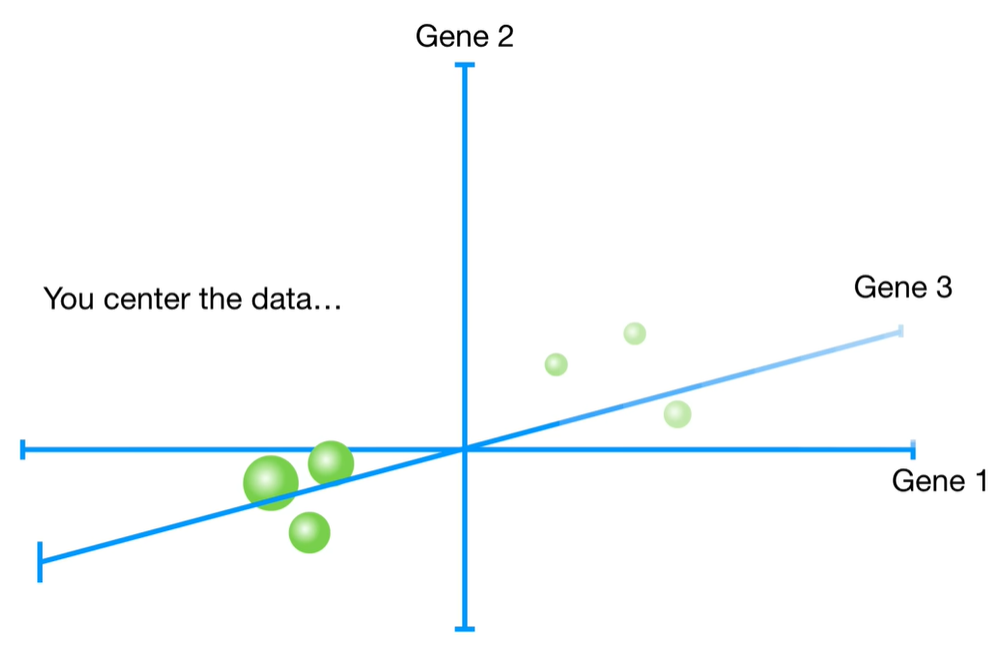
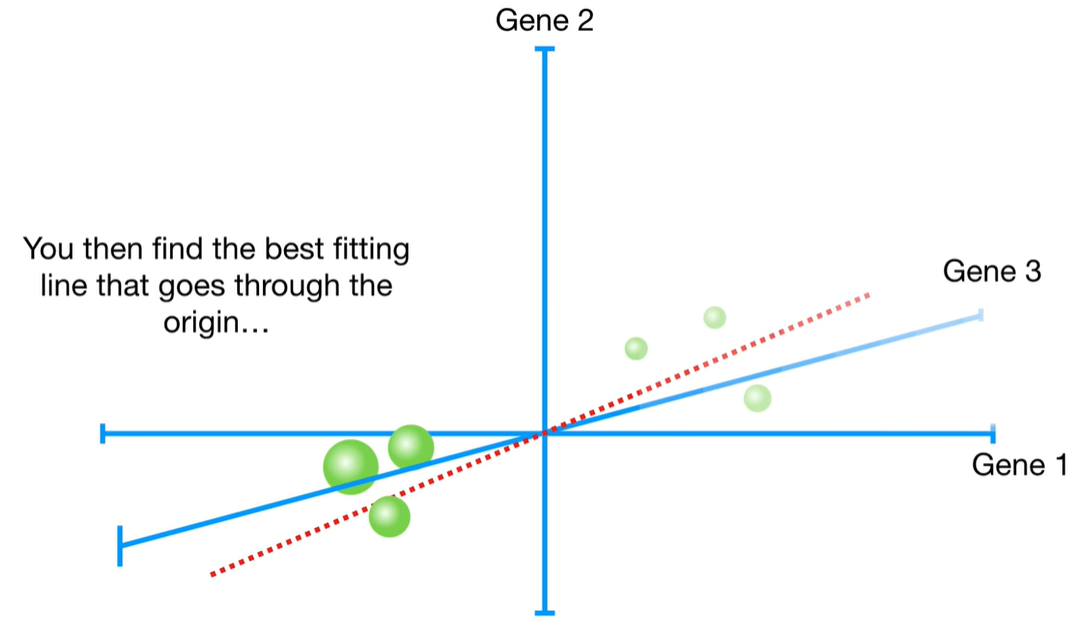
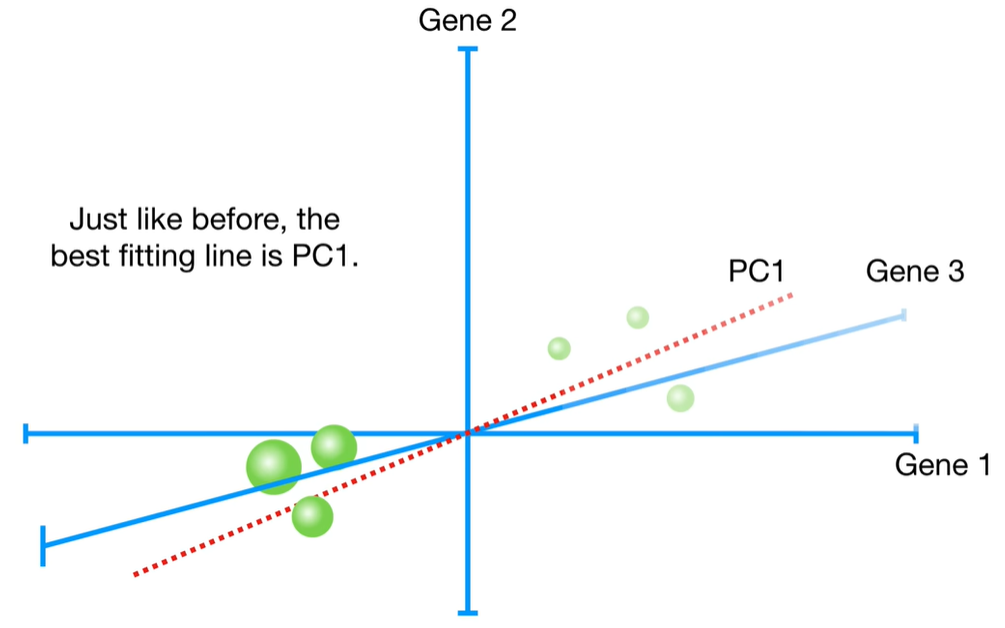
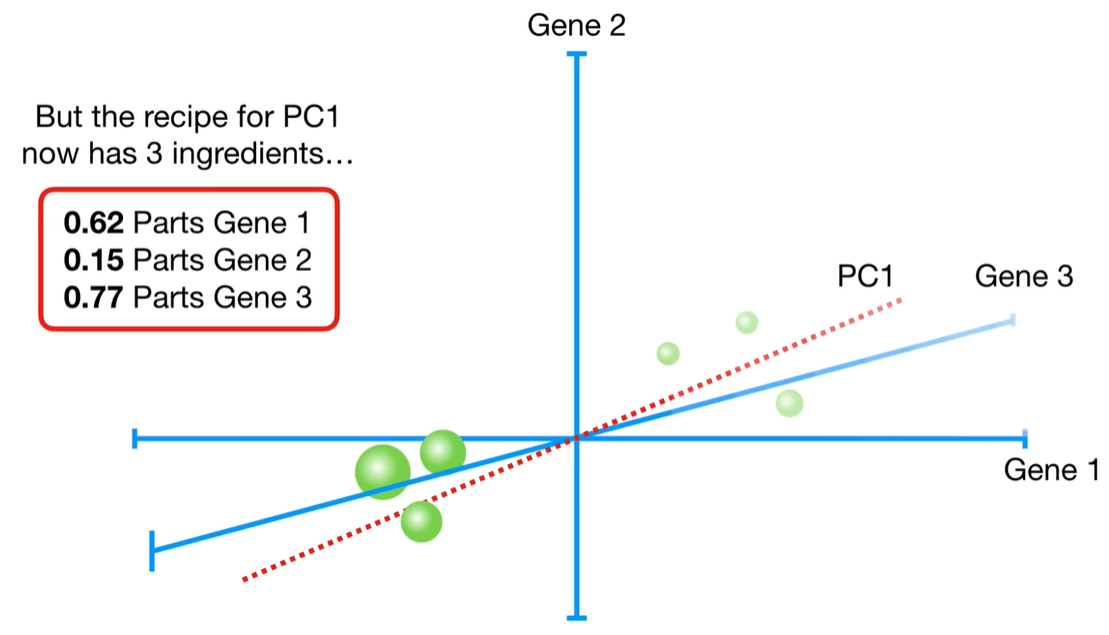








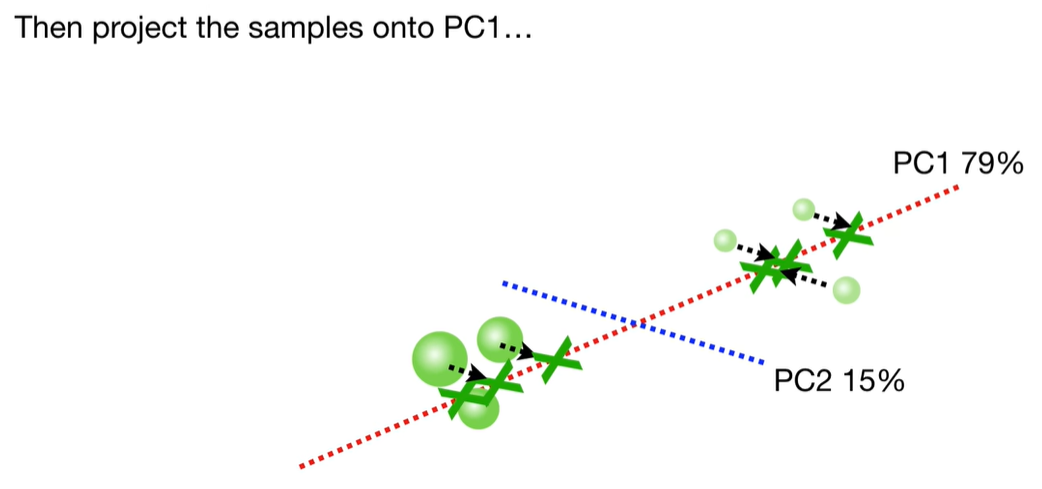

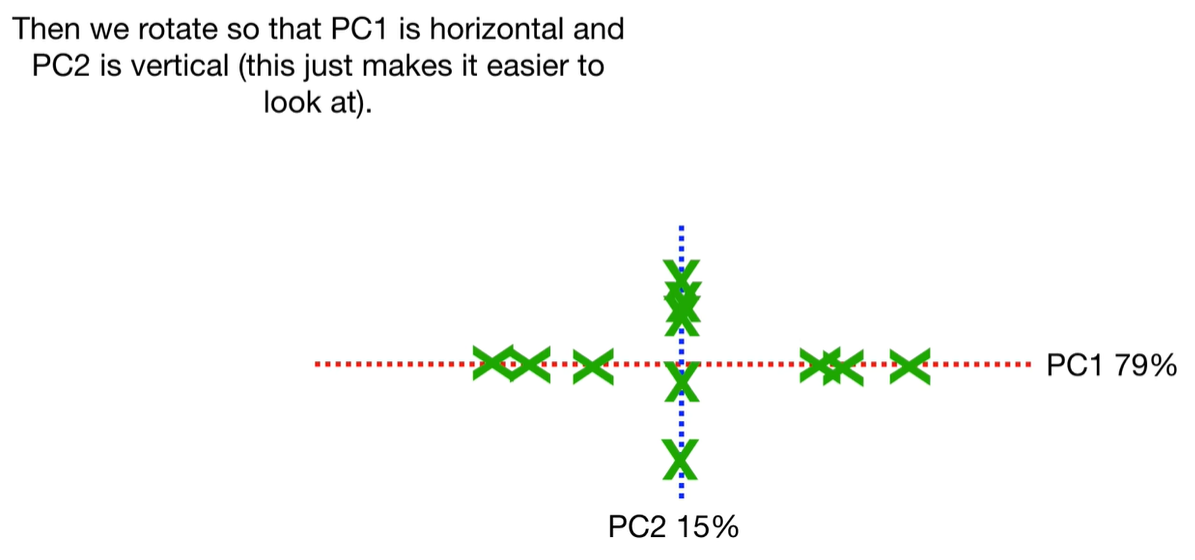

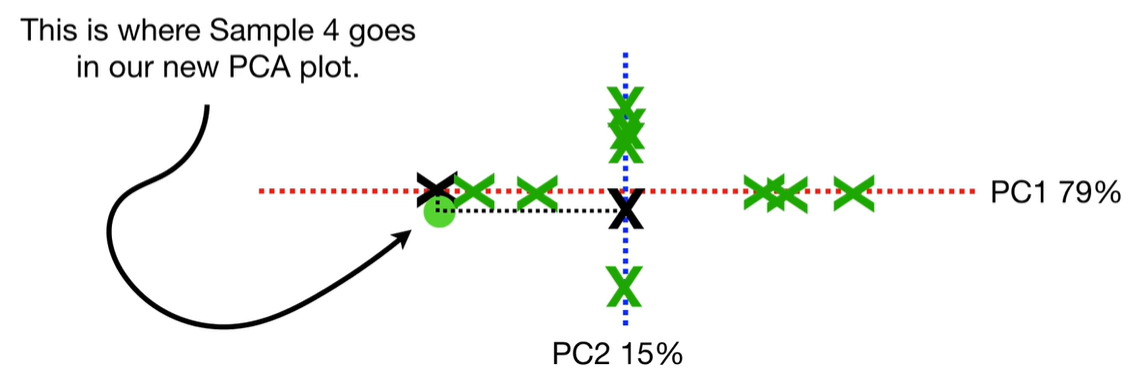
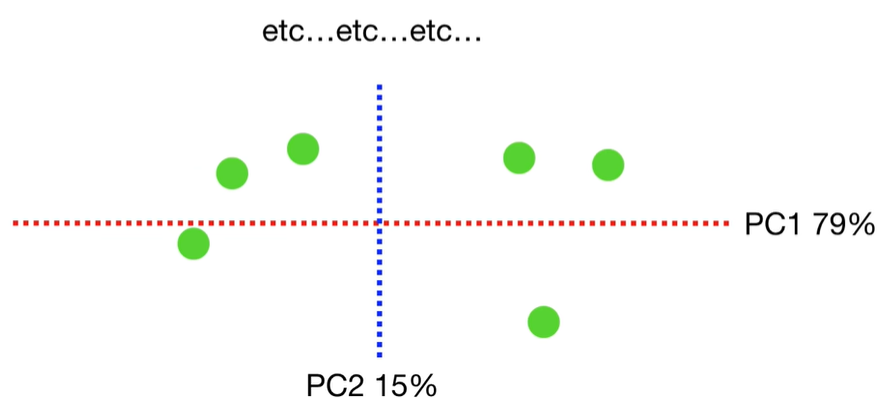
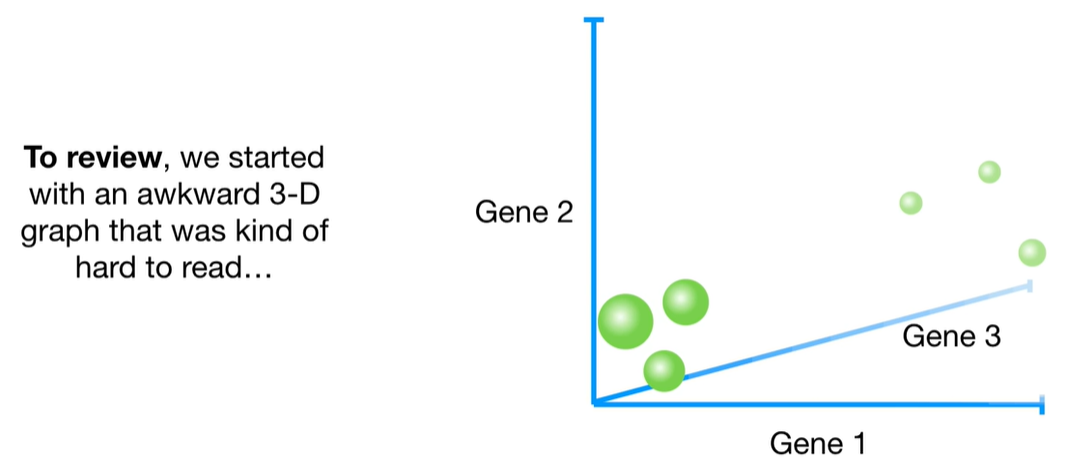
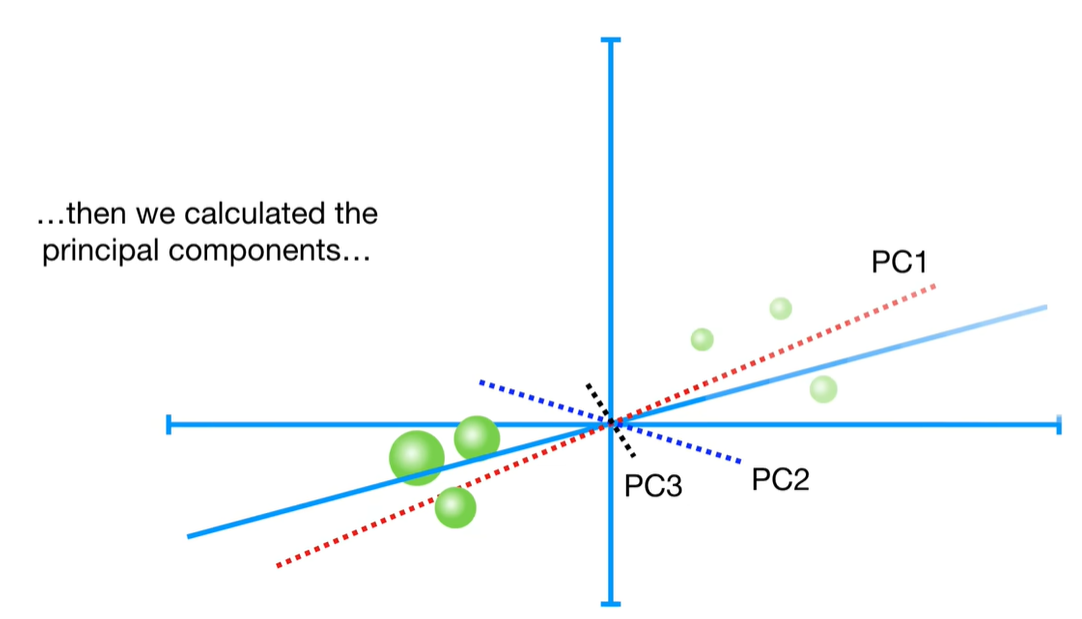
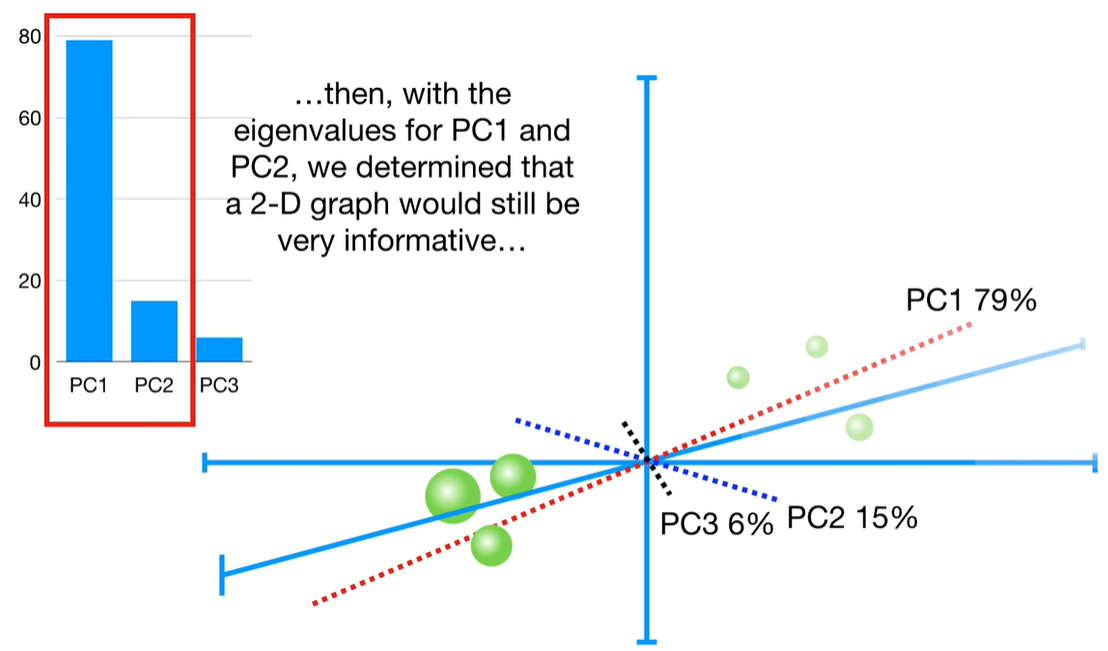
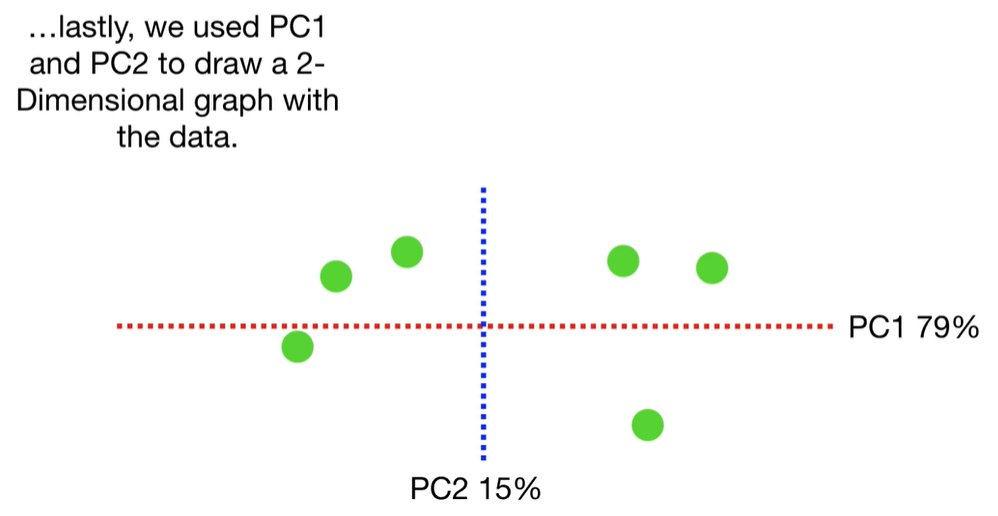






 浙公网安备 33010602011771号
浙公网安备 33010602011771号