LASSO regression (short for Least Absolute Shrinkage and Selection Operator) is a type of linear regression that performs both regularization and feature selection.
🔍 How it works
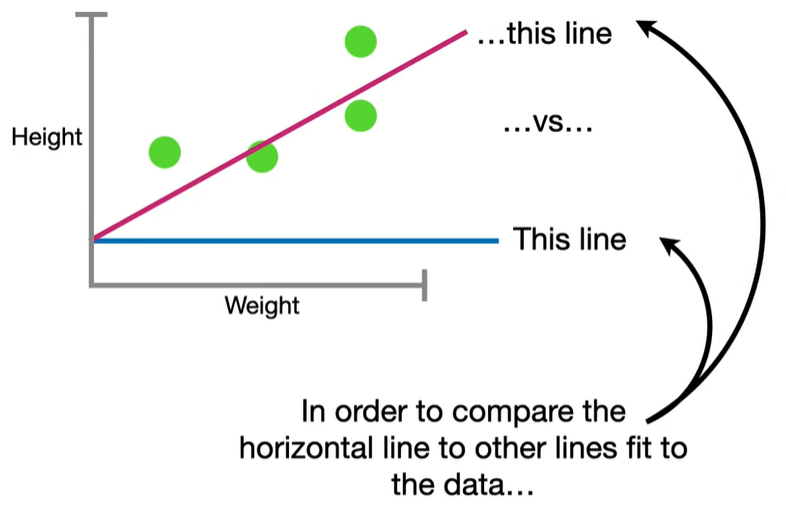
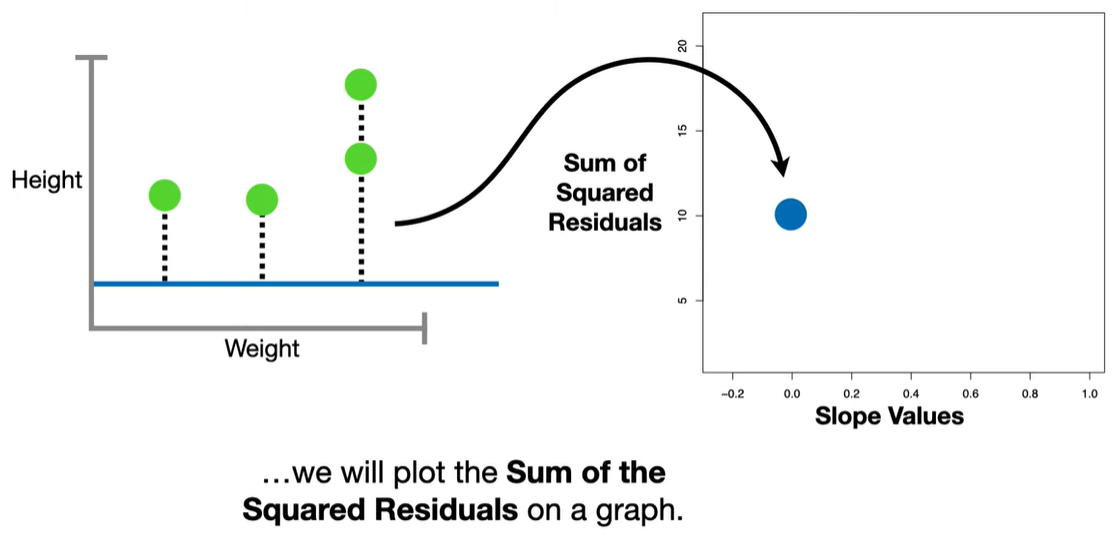
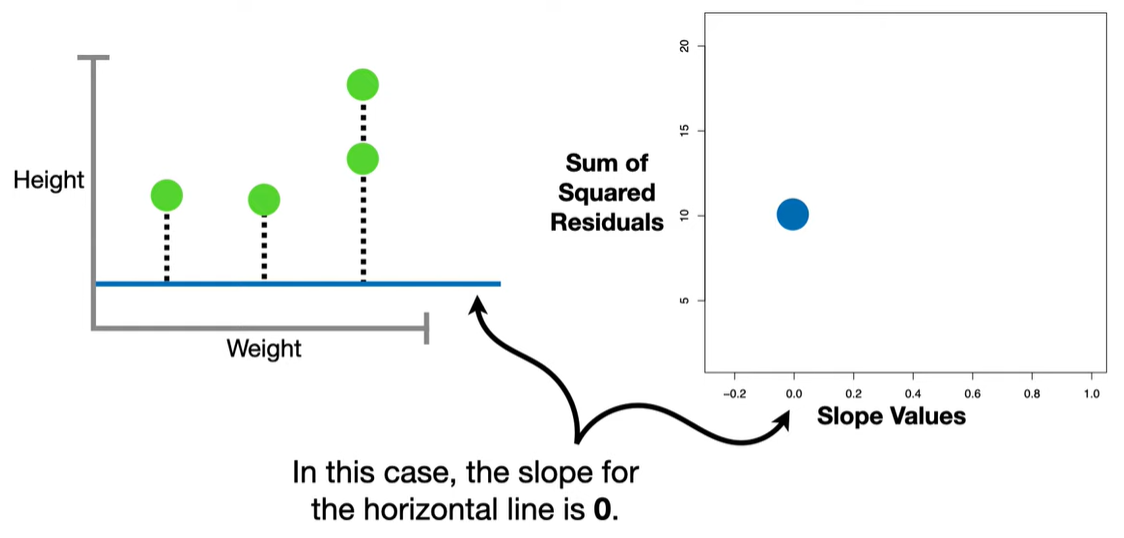
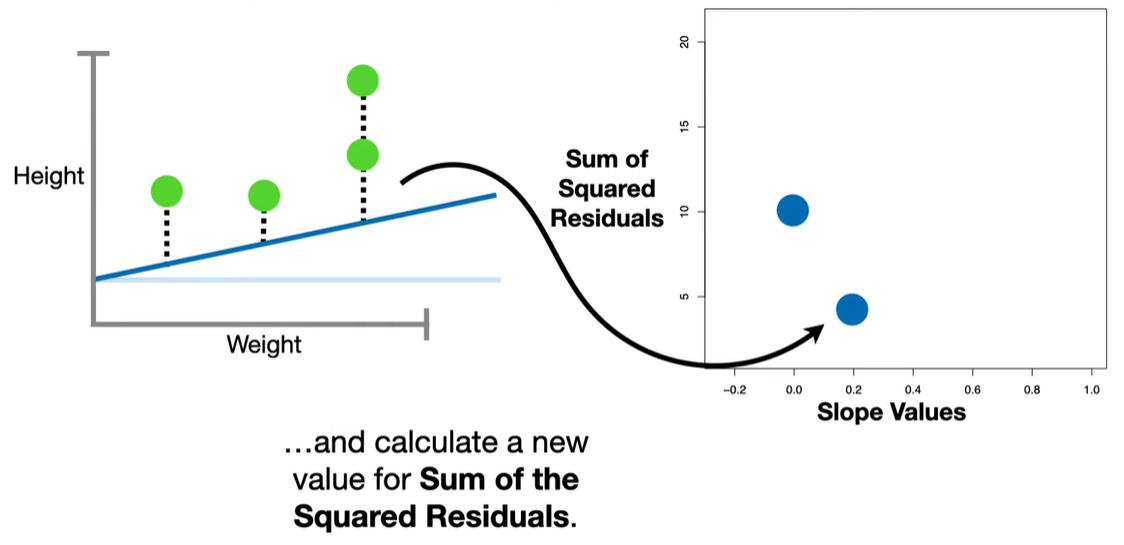
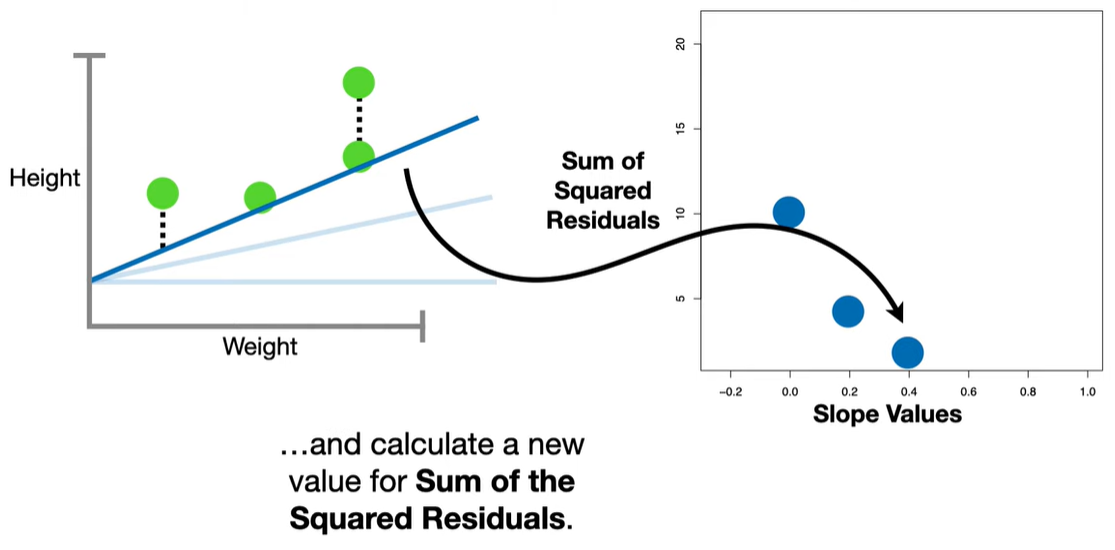
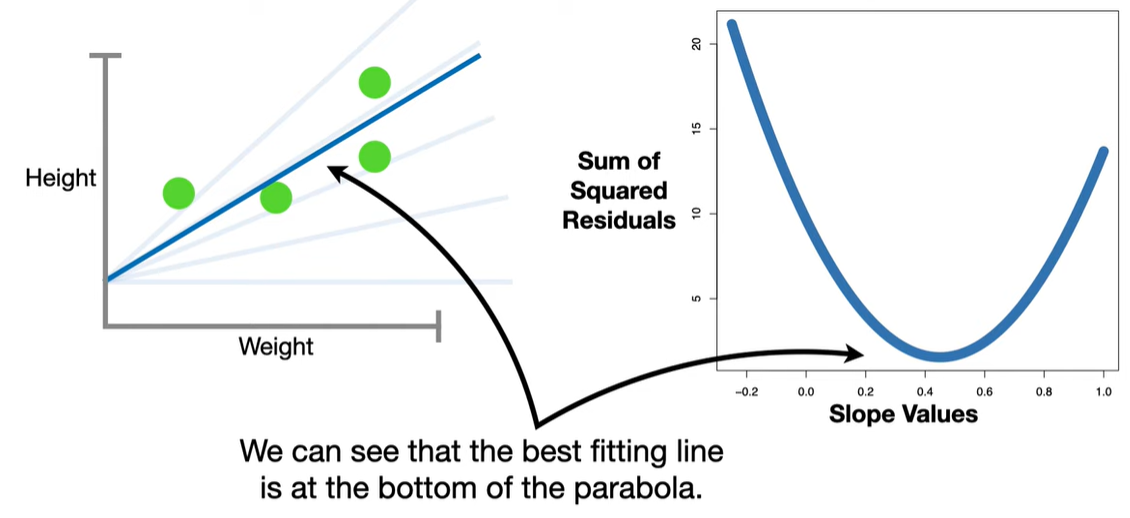
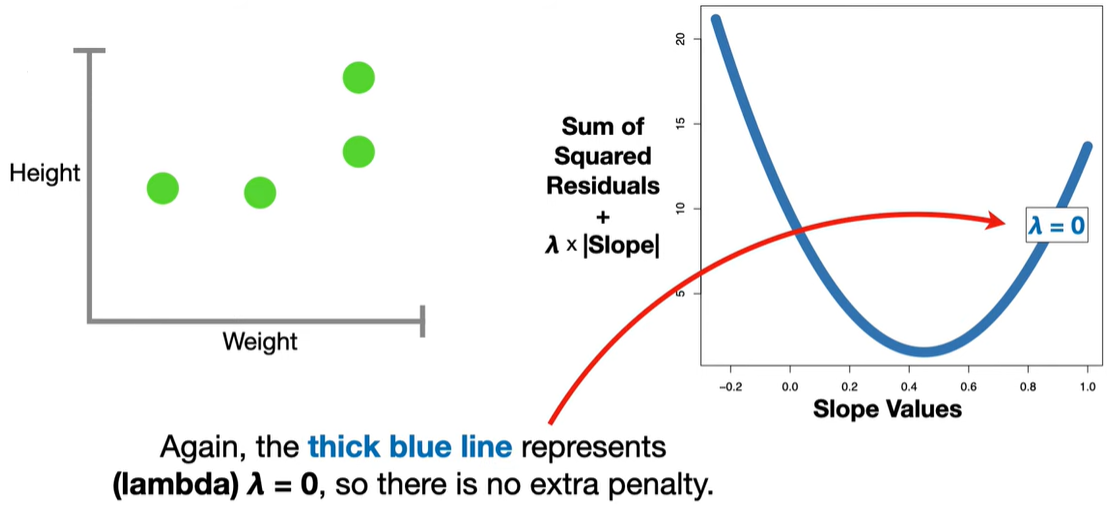
In standard linear regression, we try to minimize the residual sum of squares (RSS):
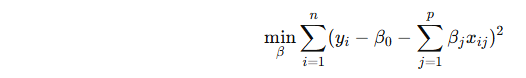
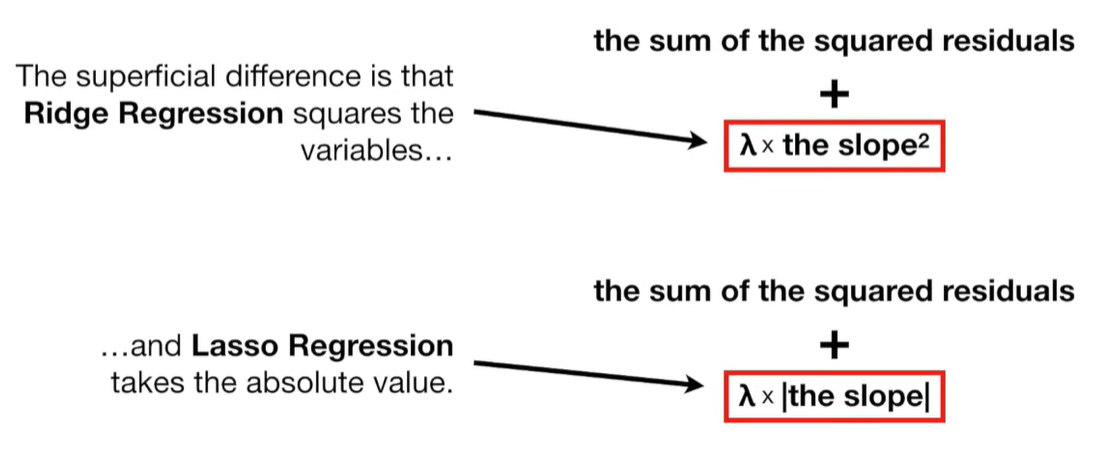
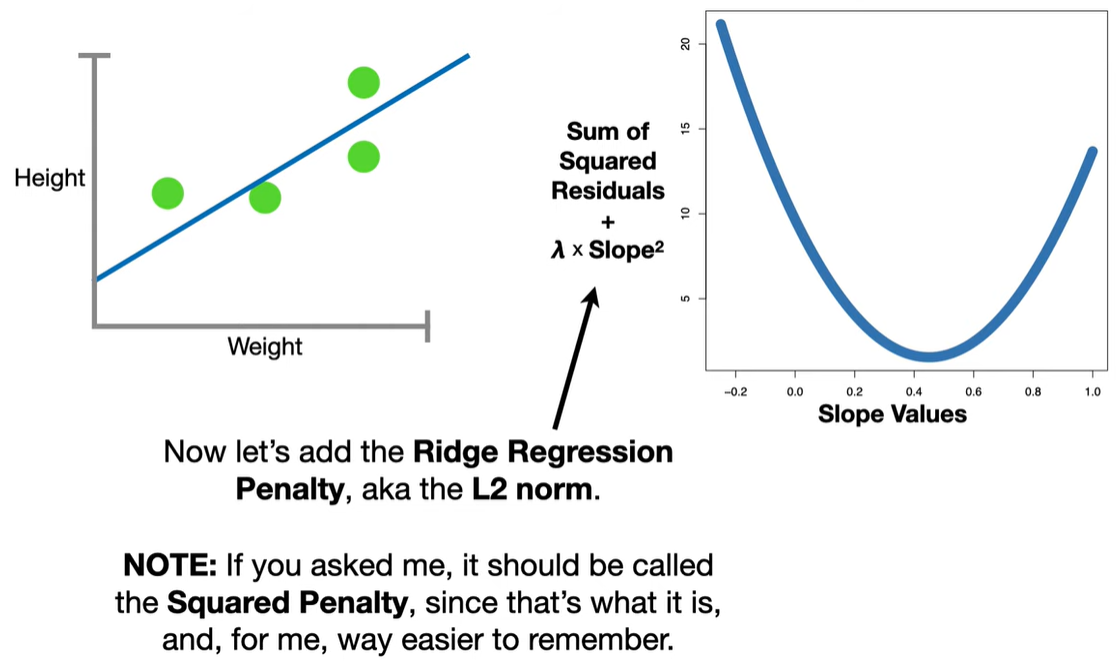
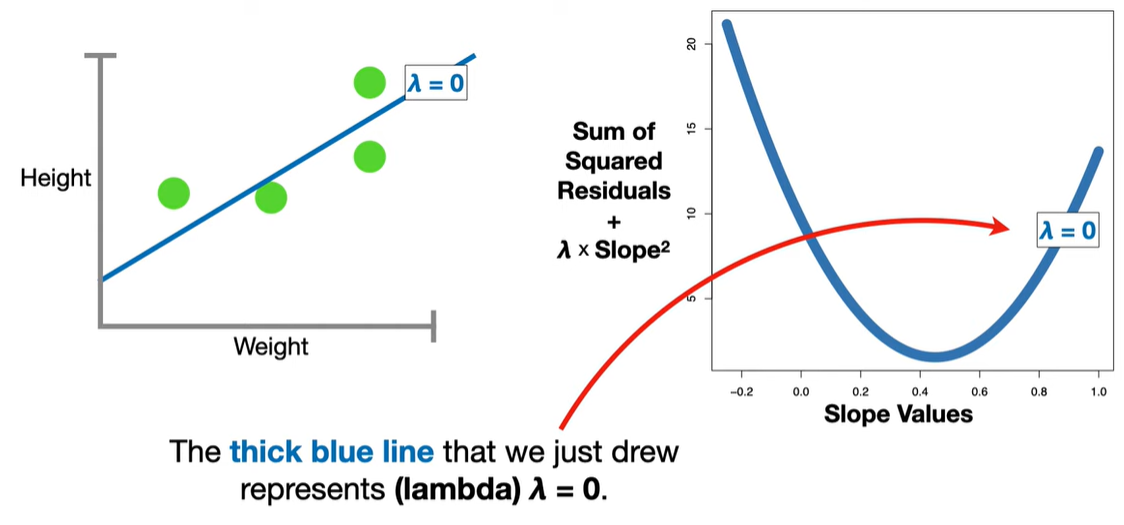
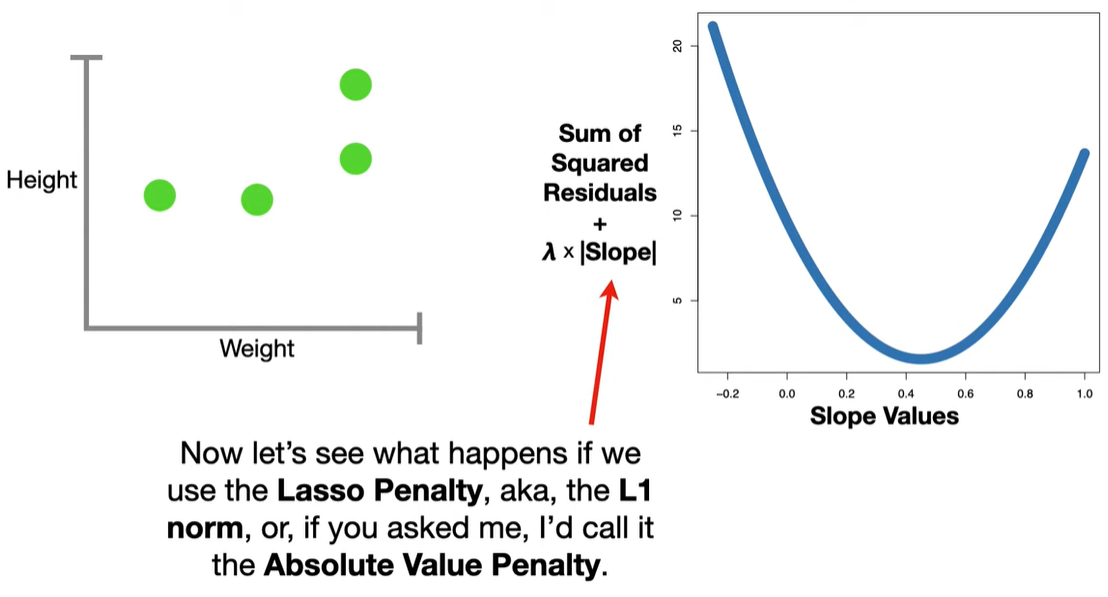
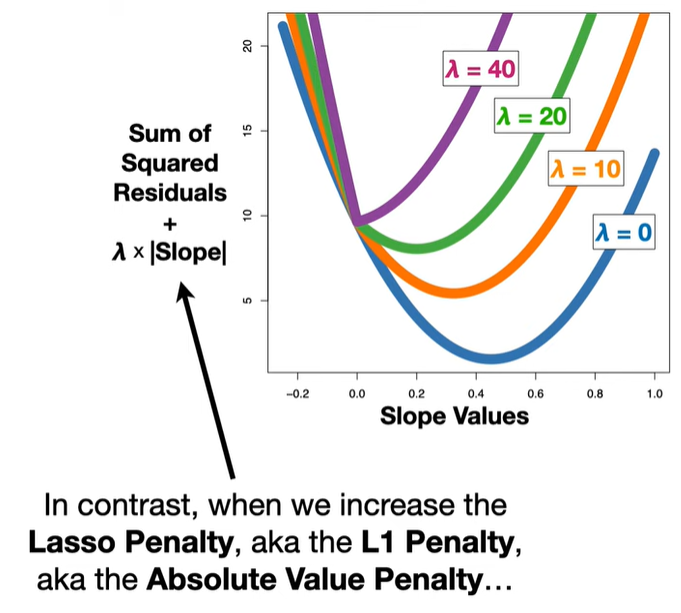
LASSO modifies this by adding a penalty term based on the L1 norm (sum of absolute values of the coefficients):

📌 Key Characteristics
-
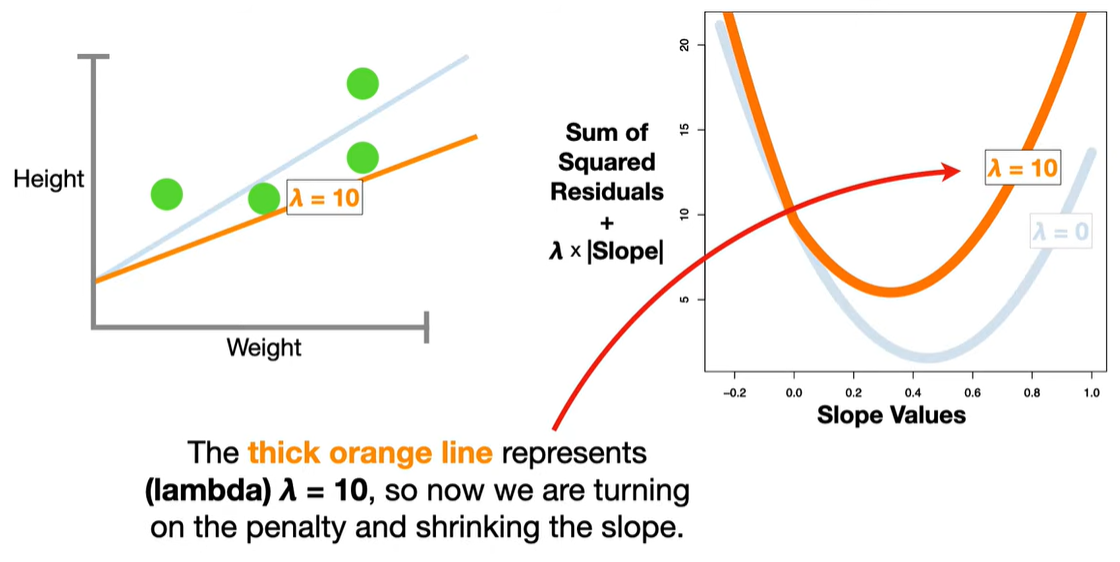
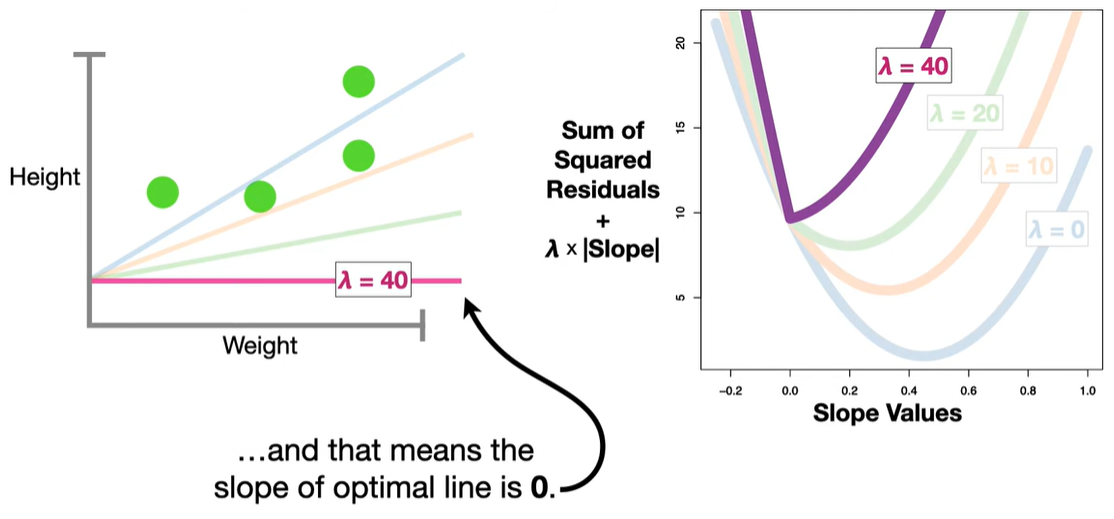
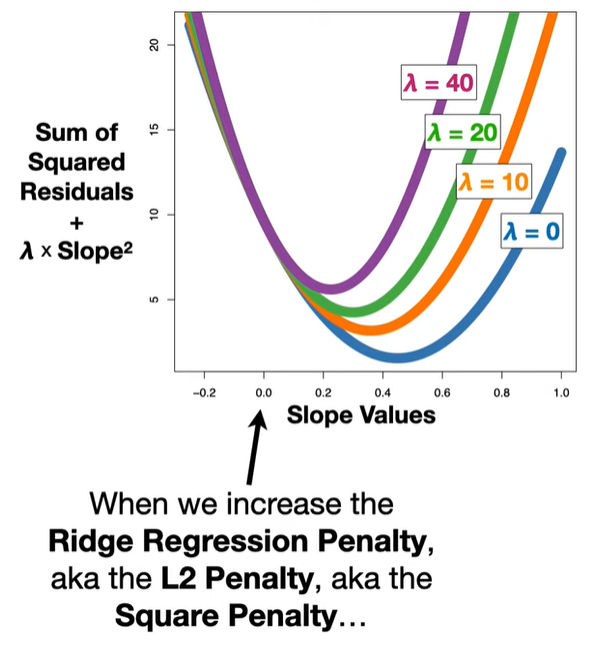
Shrinkage: Coefficients are shrunk toward zero, reducing model complexity and preventing overfitting.
-
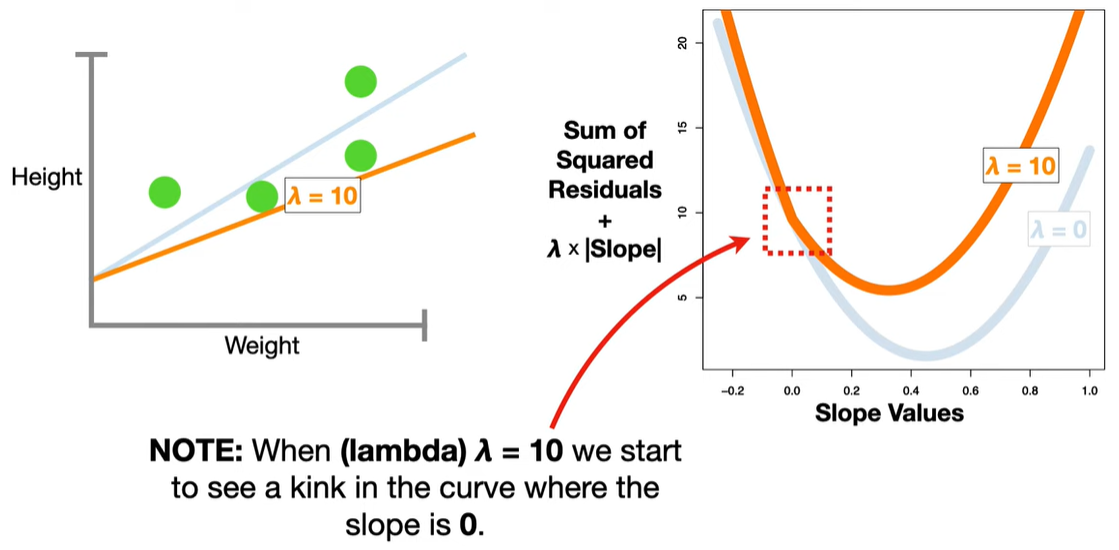
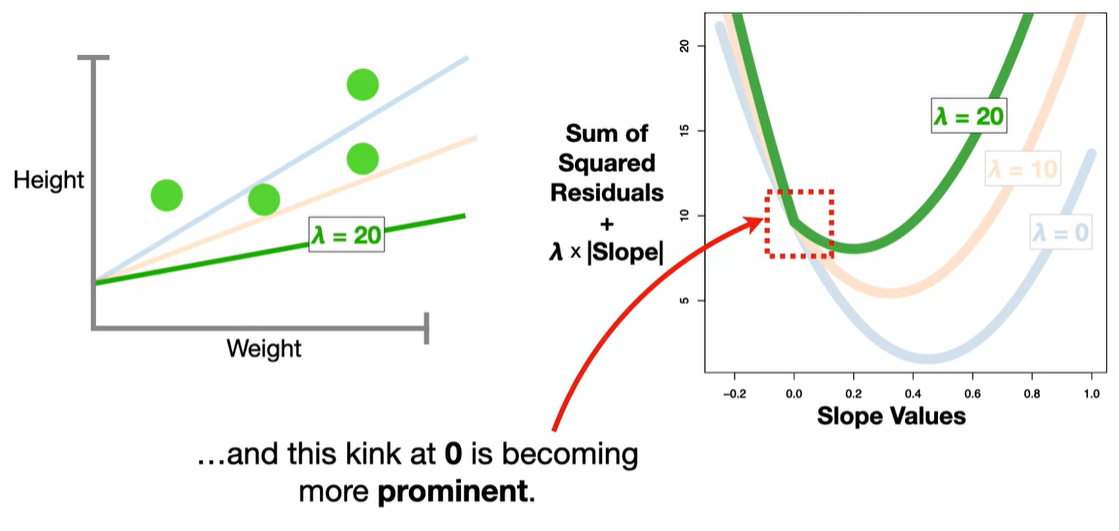
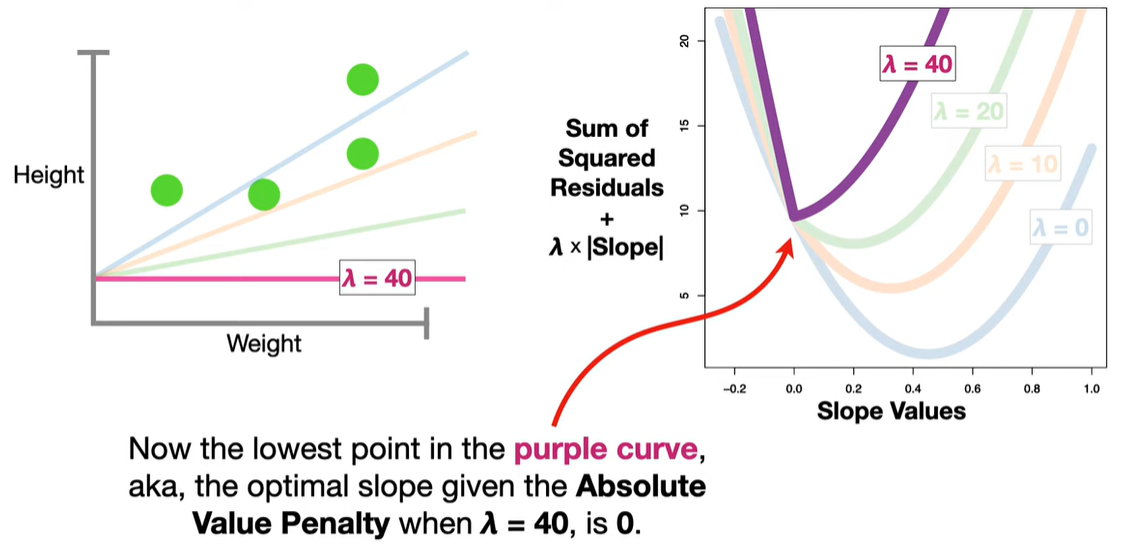
Sparsity (Feature Selection): Some coefficients are driven exactly to zero, effectively removing those variables from the model. This makes LASSO useful when you suspect many features are irrelevant.
-
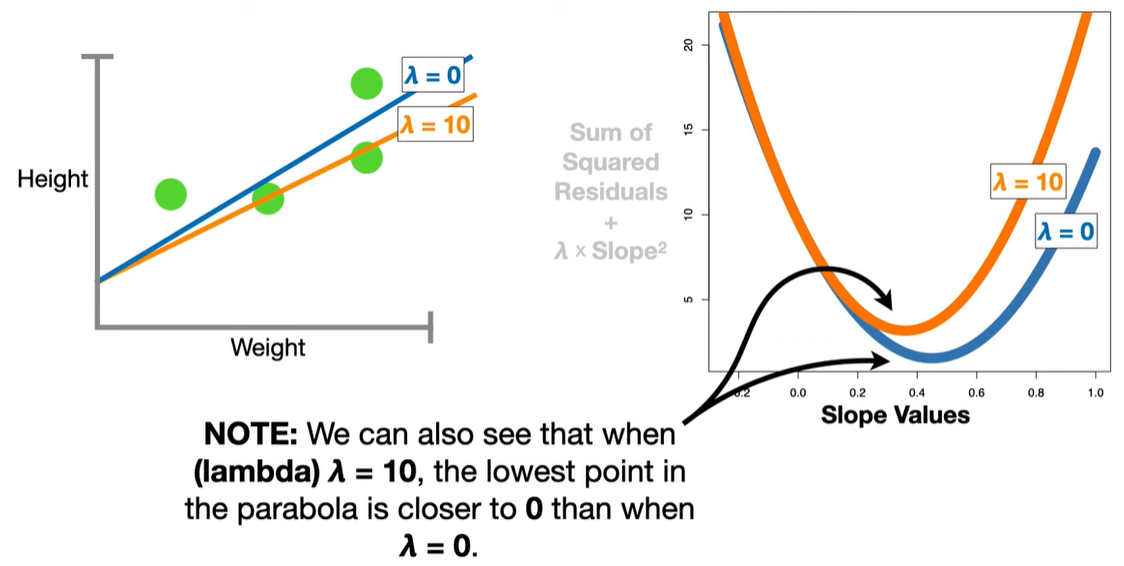
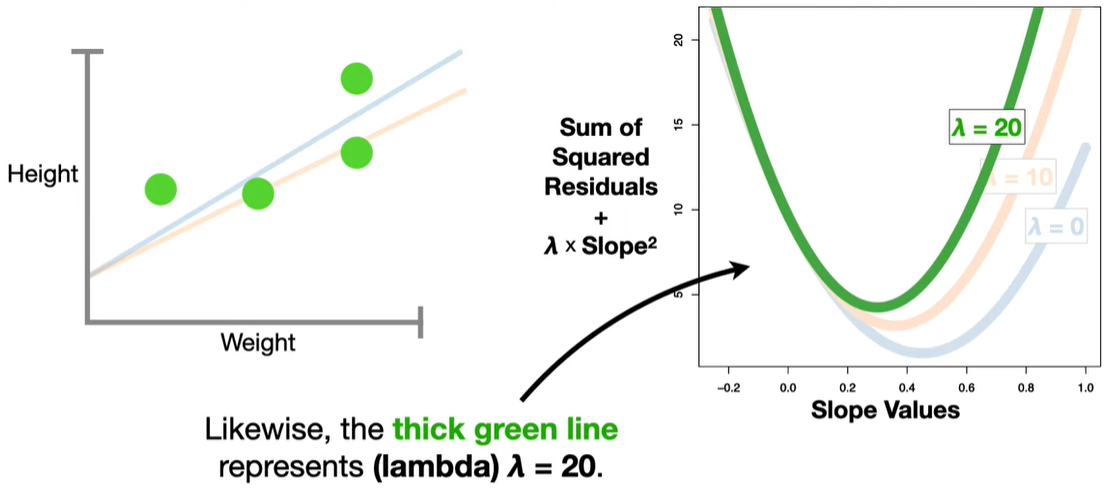
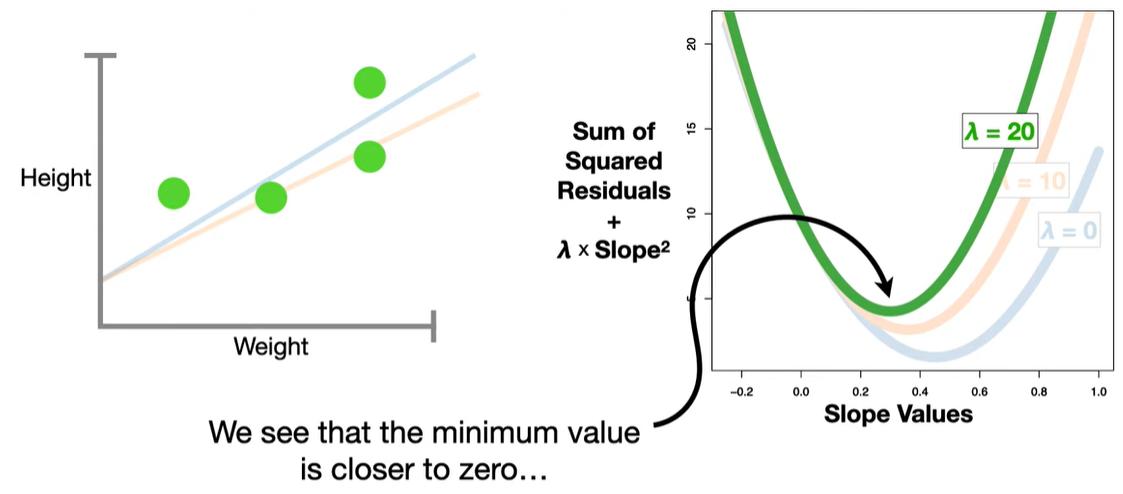
Bias-Variance Tradeoff: Introduces bias but can significantly reduce variance, often improving prediction accuracy on new data.
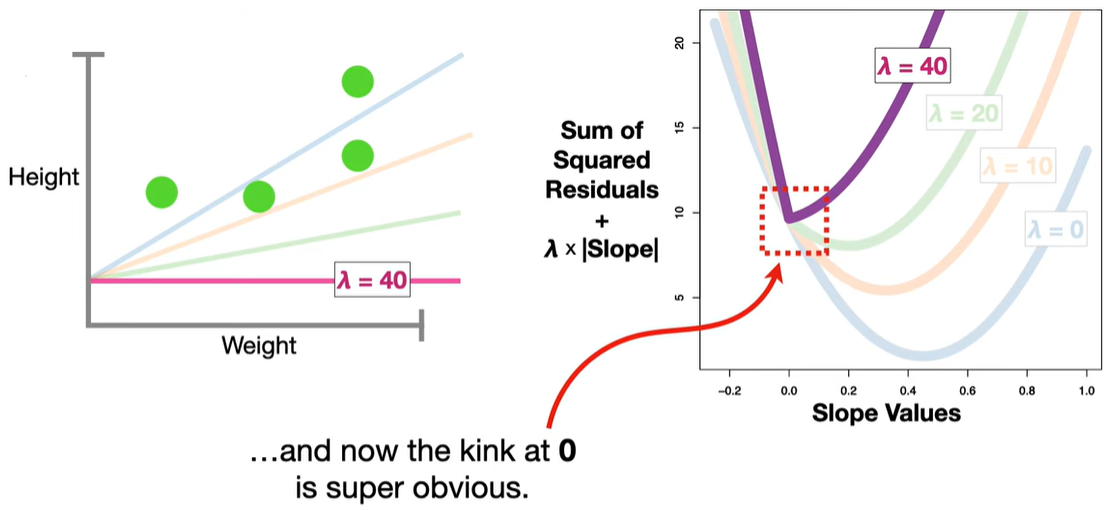
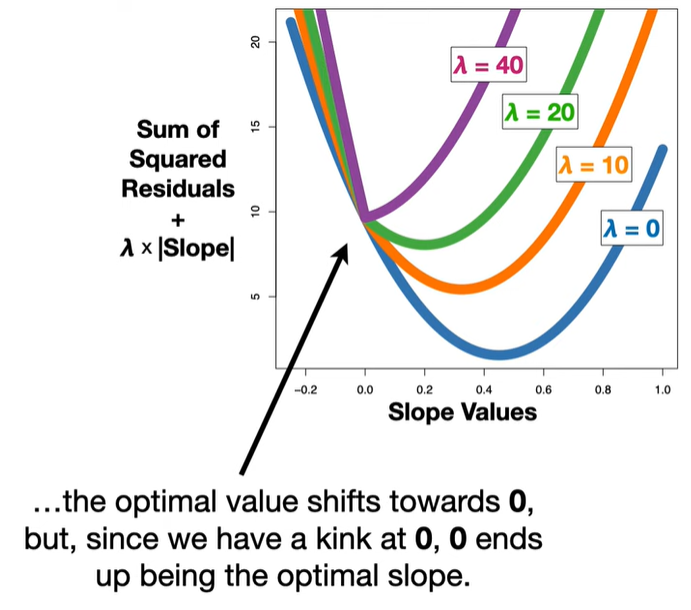
🔬 Why can LASSO set coefficients to zero?
The L1 penalty introduces non-differentiable “kinks” at zero. When minimizing the objective function, these kinks cause some coefficients to land exactly at zero, unlike Ridge regression (which uses an L2 norm and only shrinks coefficients but doesn’t zero them out).
📈 Example Use Cases
-
High-dimensional datasets (e.g., genomics, text classification) where the number of predictors exceeds the number of observations.
-
Situations where model interpretability is important and you want to select only a subset of features.

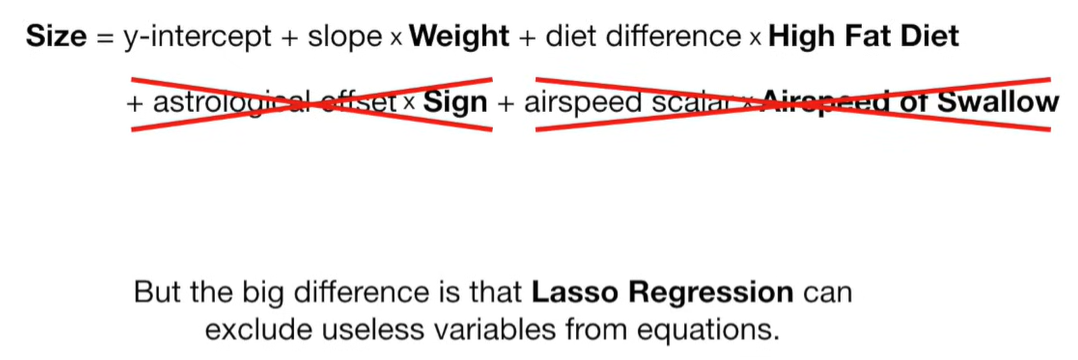













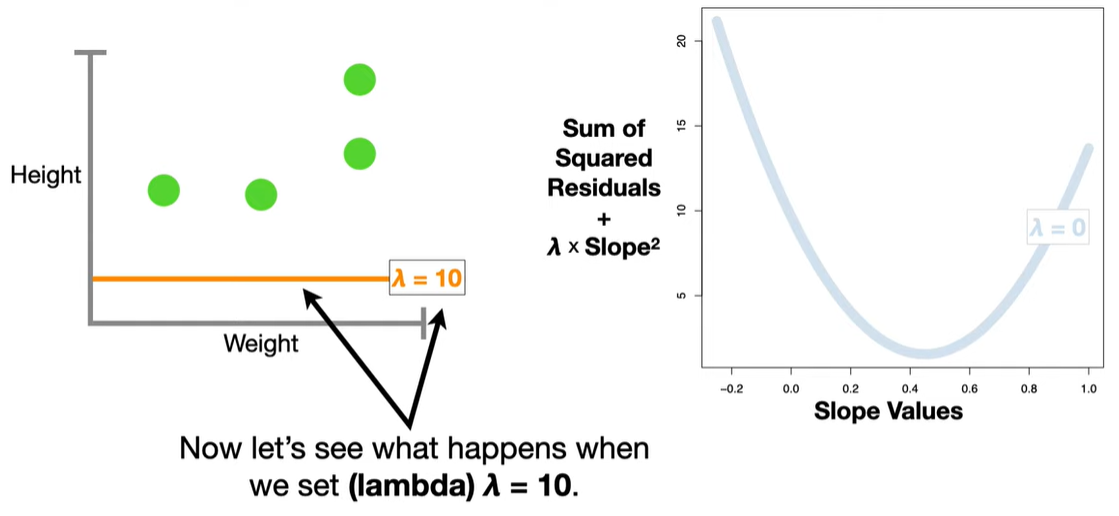

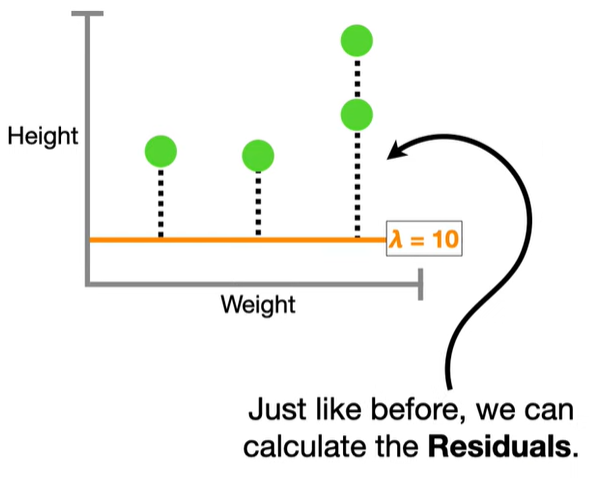




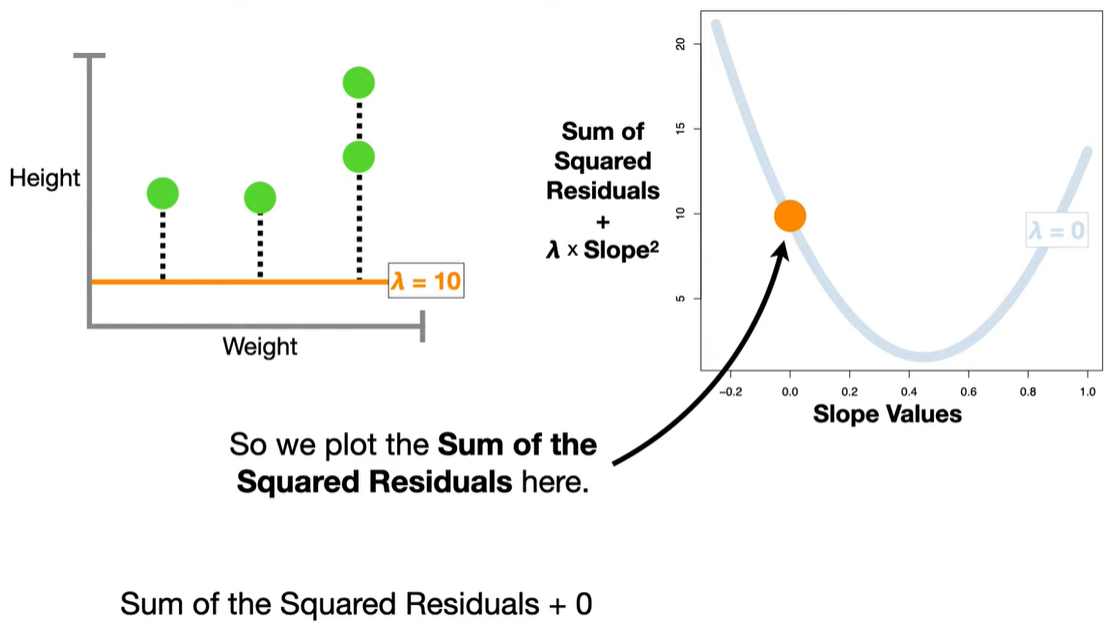

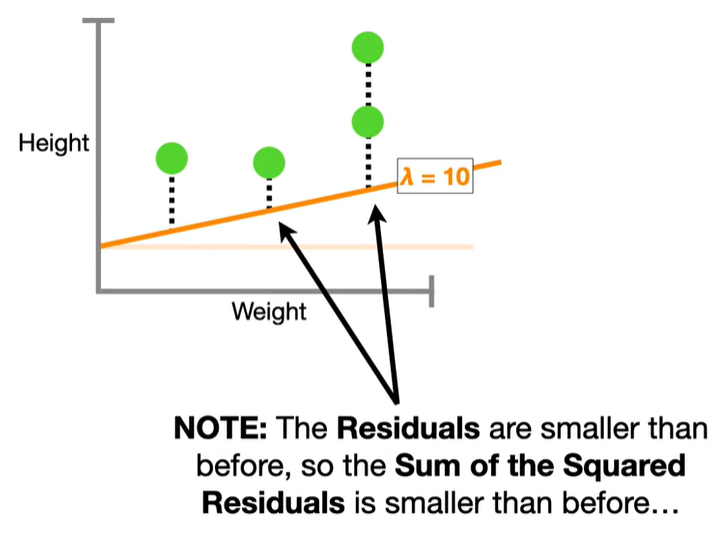




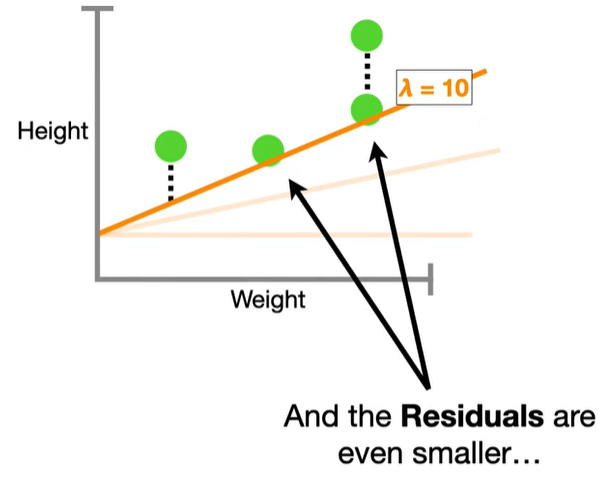



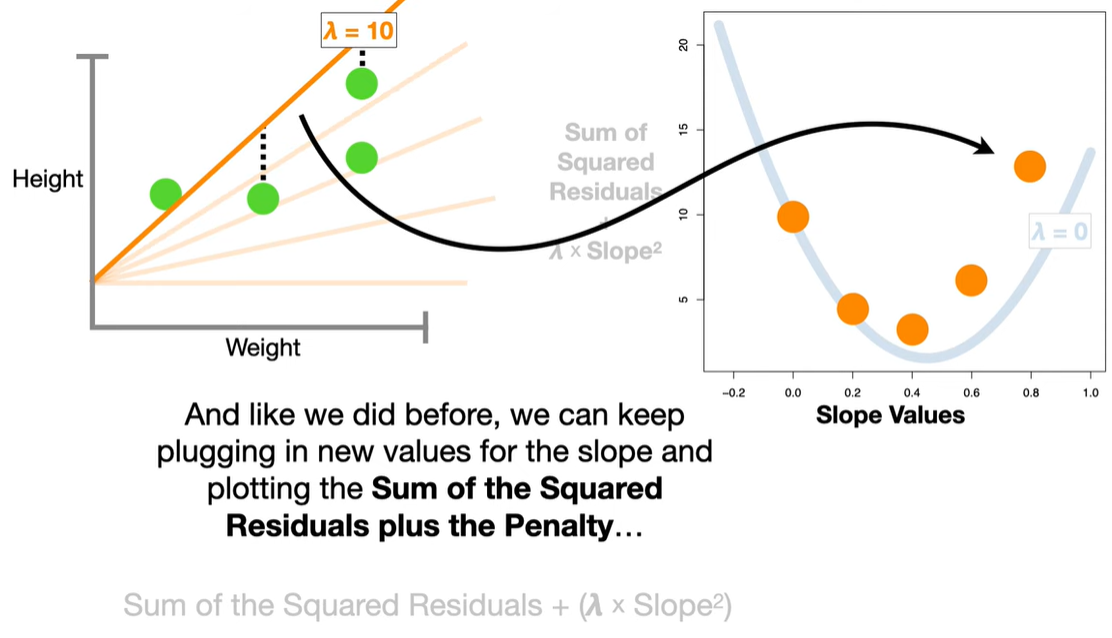
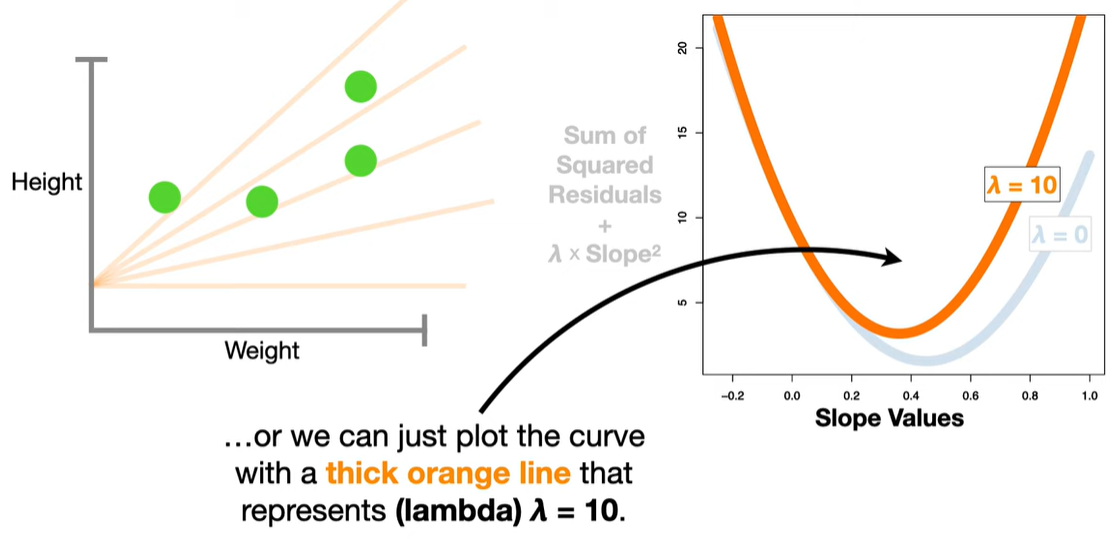

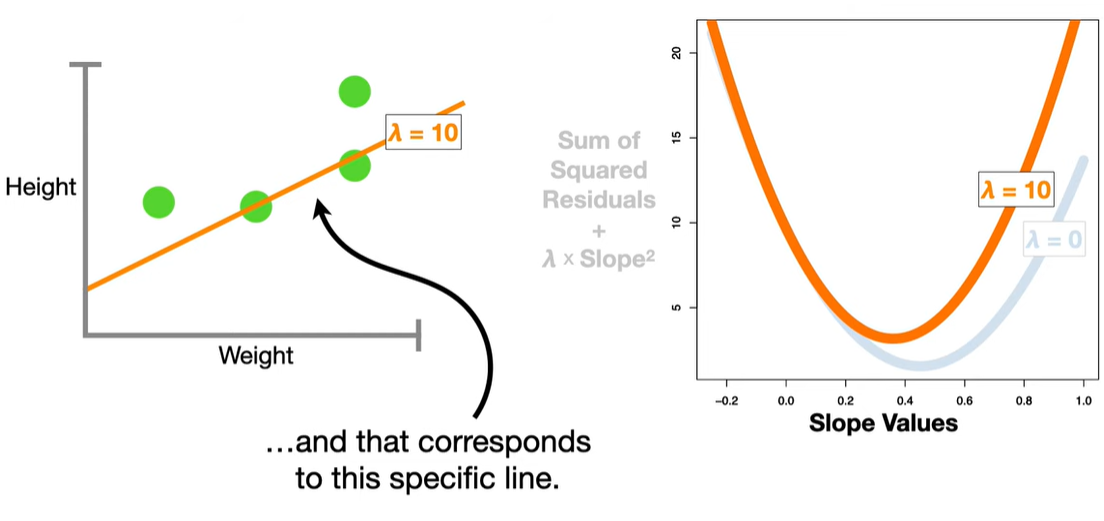












 浙公网安备 33010602011771号
浙公网安备 33010602011771号