Machine Learning - Regularization: Ridge Regression

 

 

 

 

 

 

 

 

 

 

     

 

 

     

 

 

 

     

 

 

 

 

     

 

 

     

 

 

 

 

 

 

 

 

 

 

     

 

 

 

 

 

     

 

 

     

 

     

 

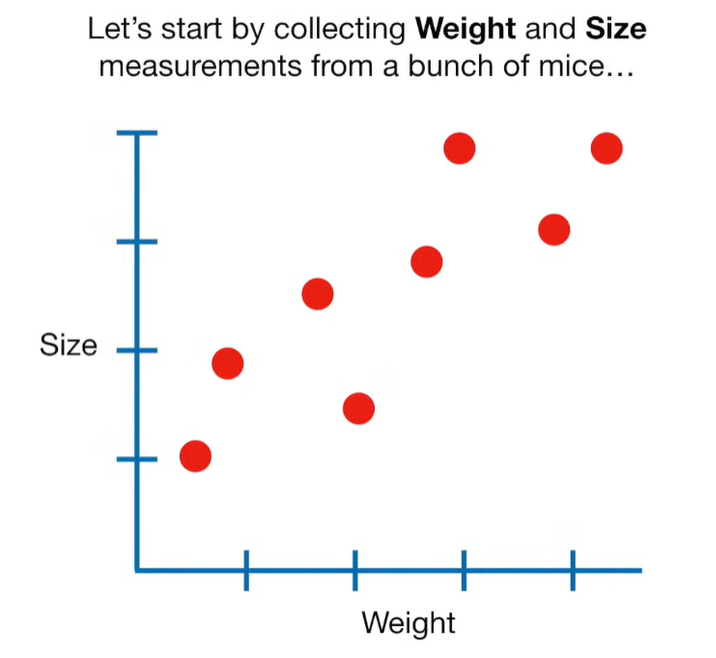
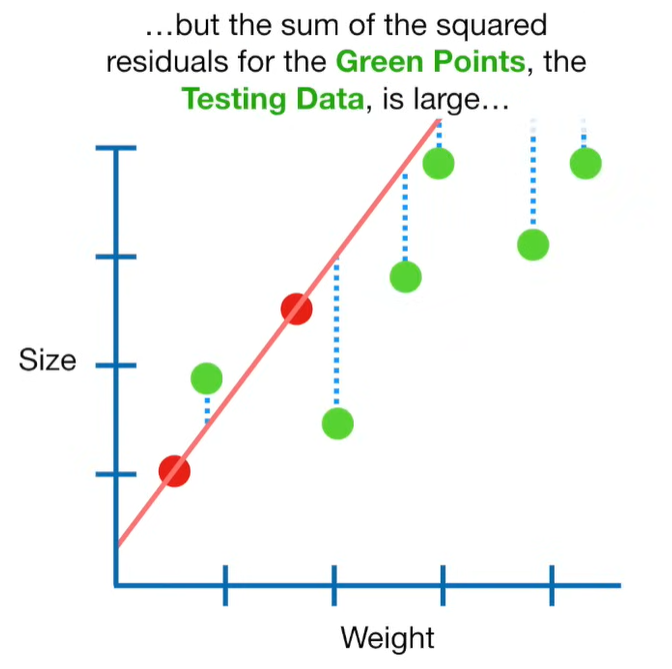
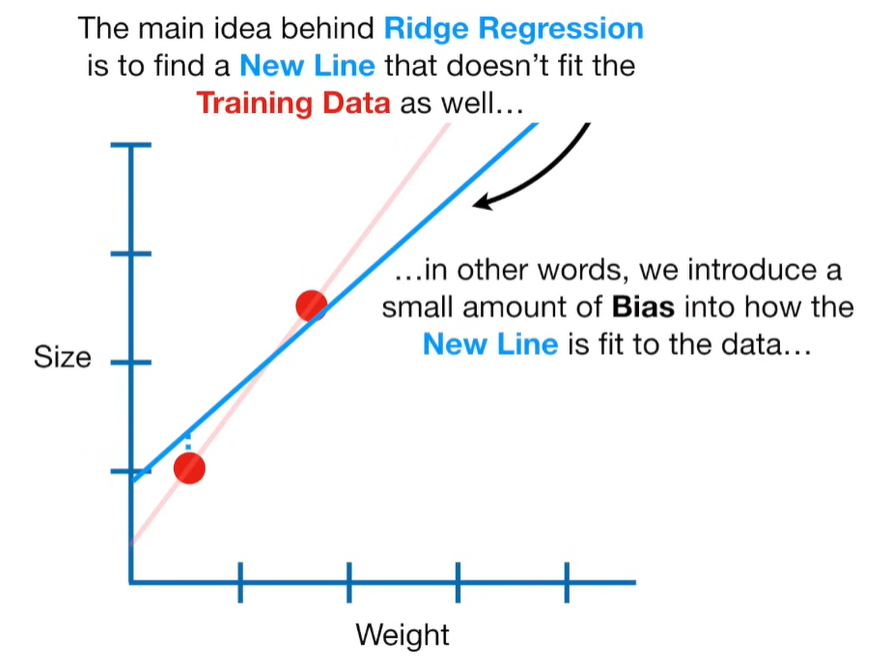
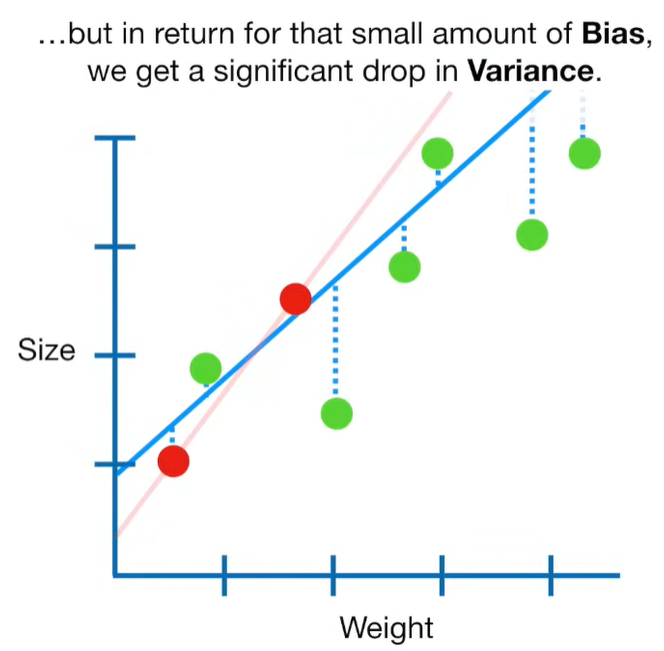
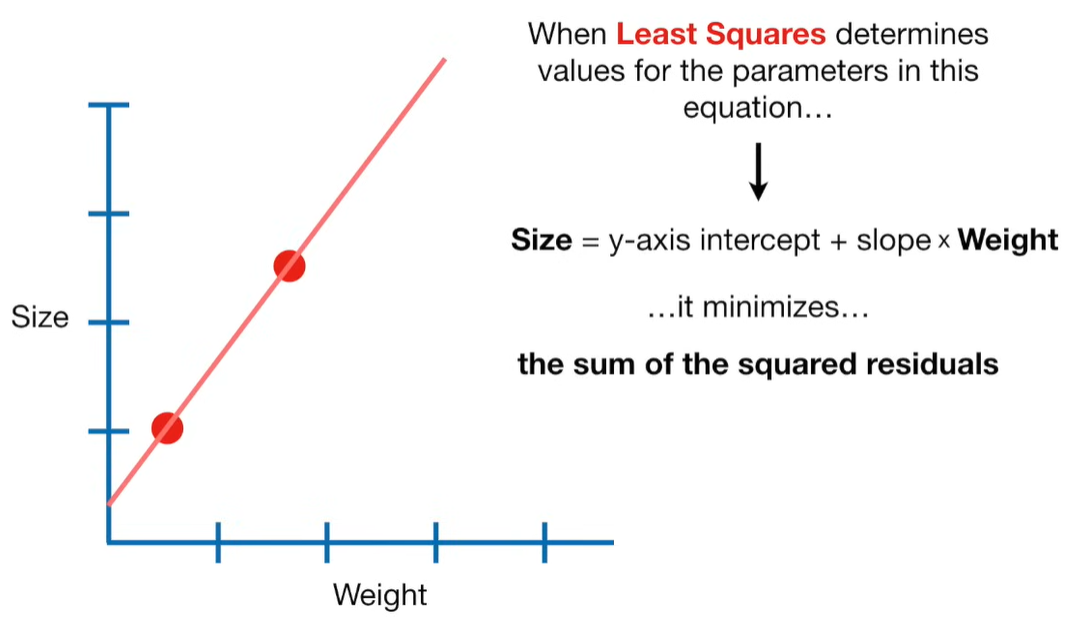
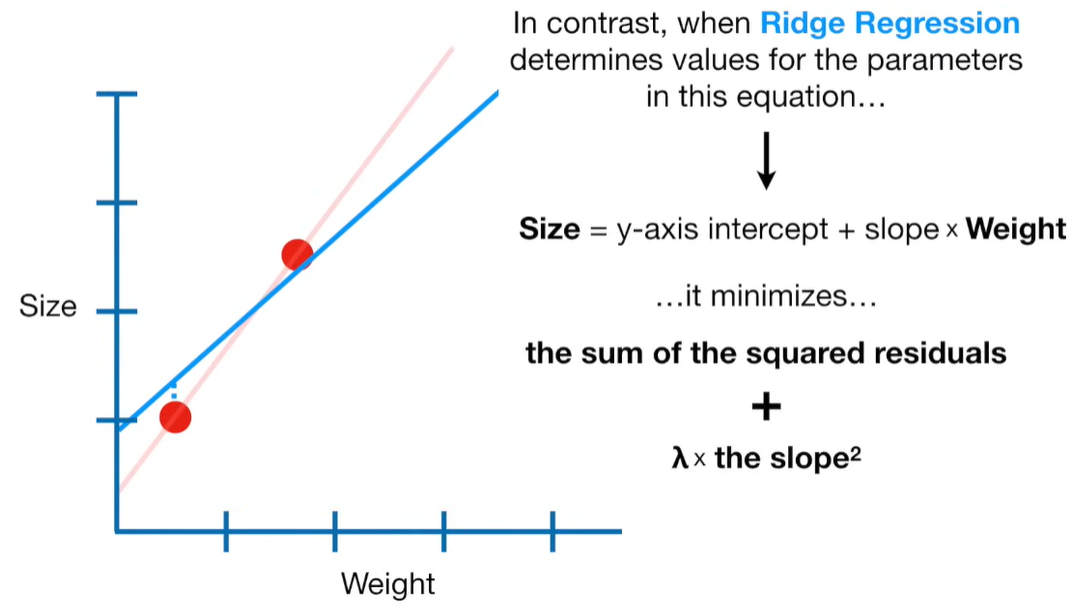
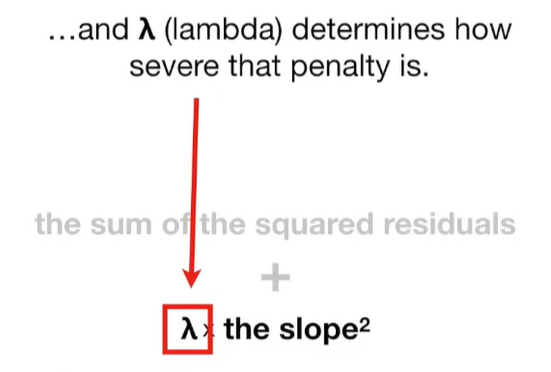
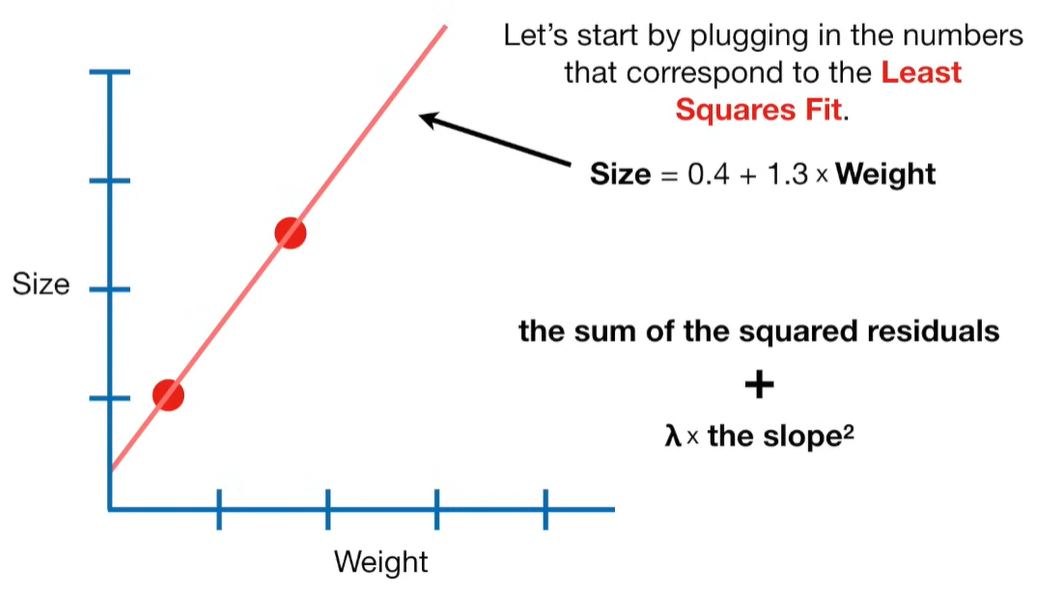
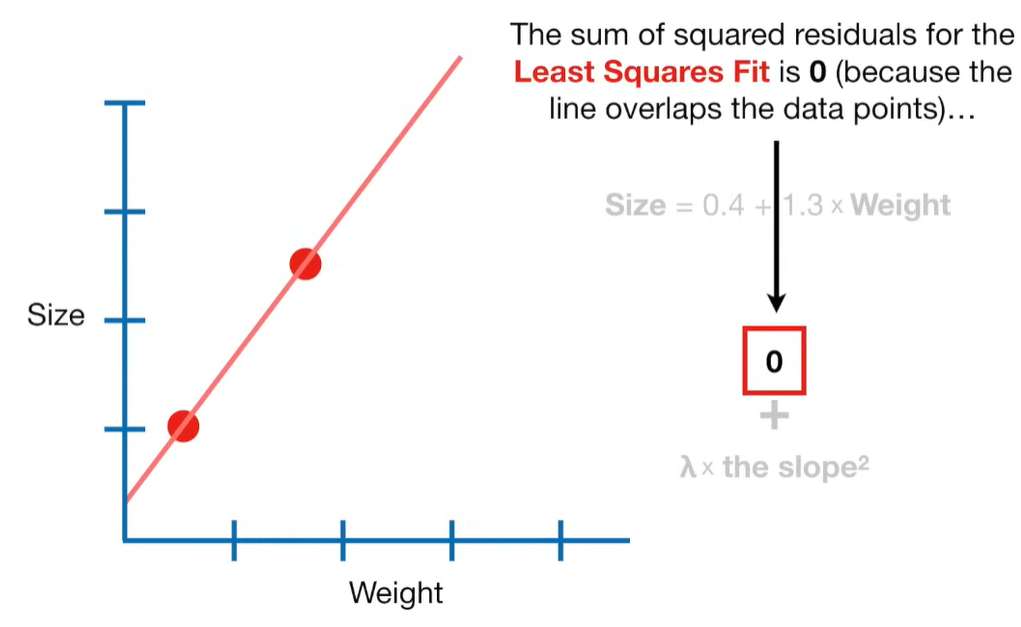
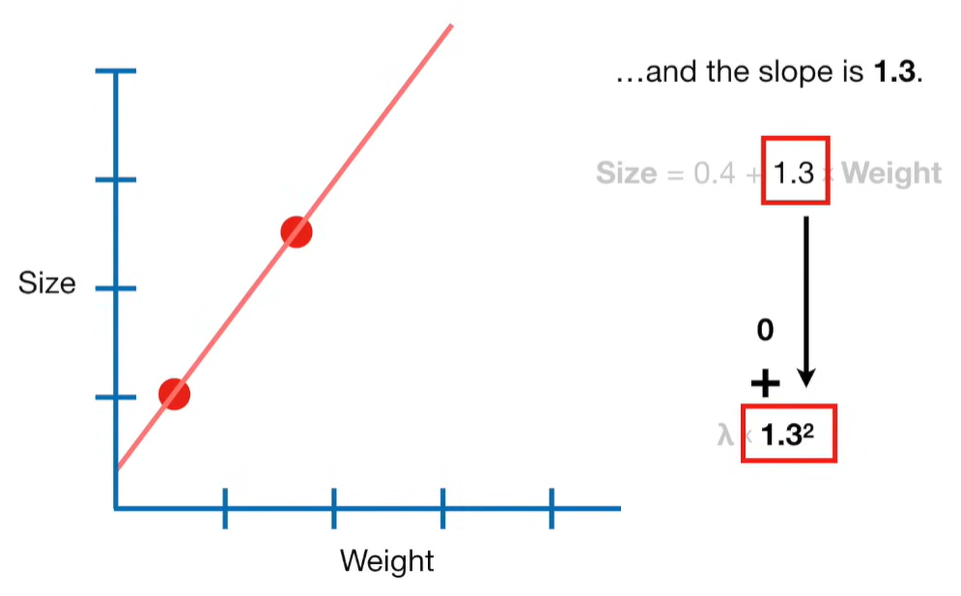
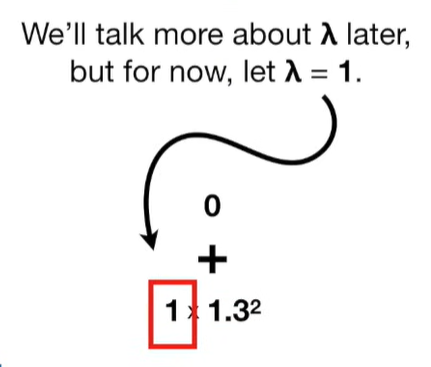
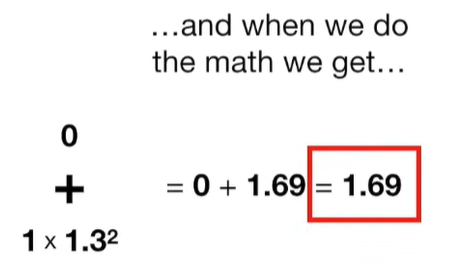
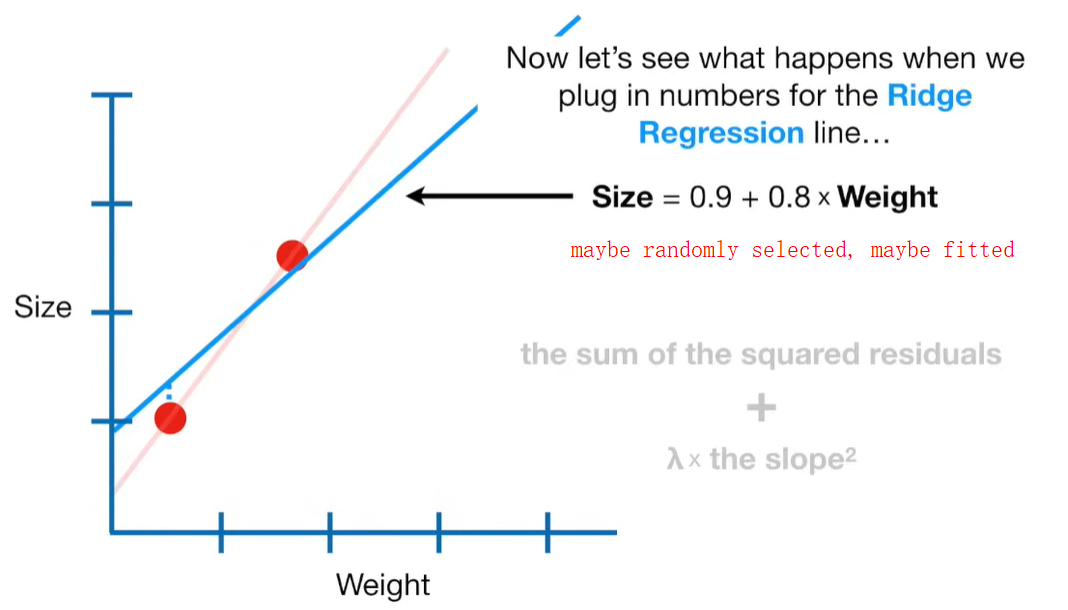
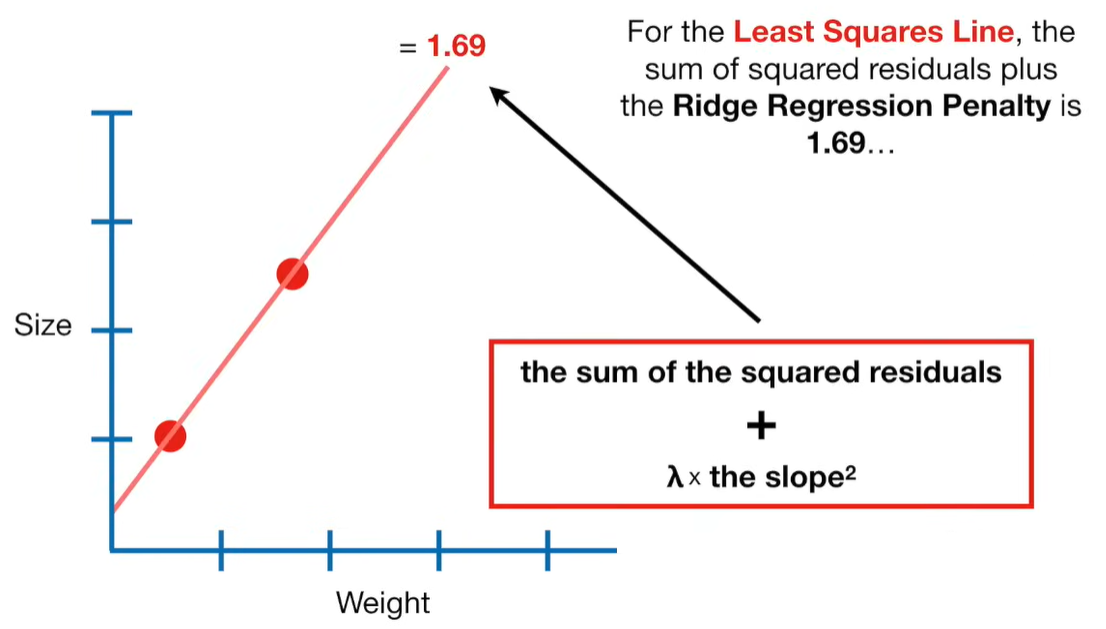
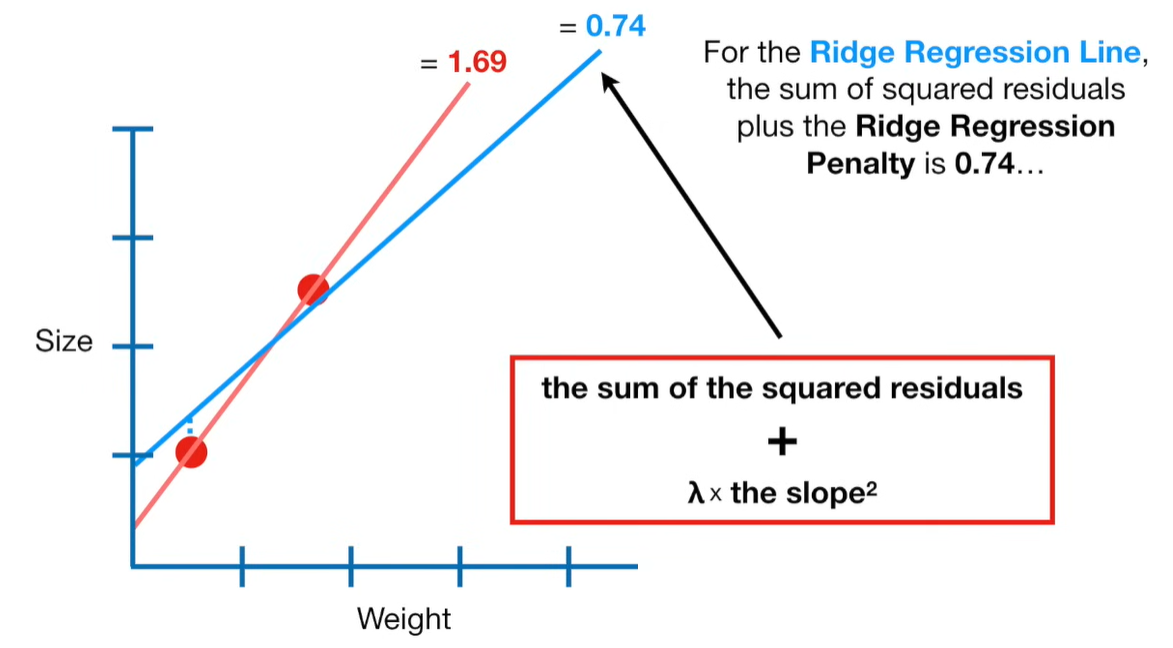
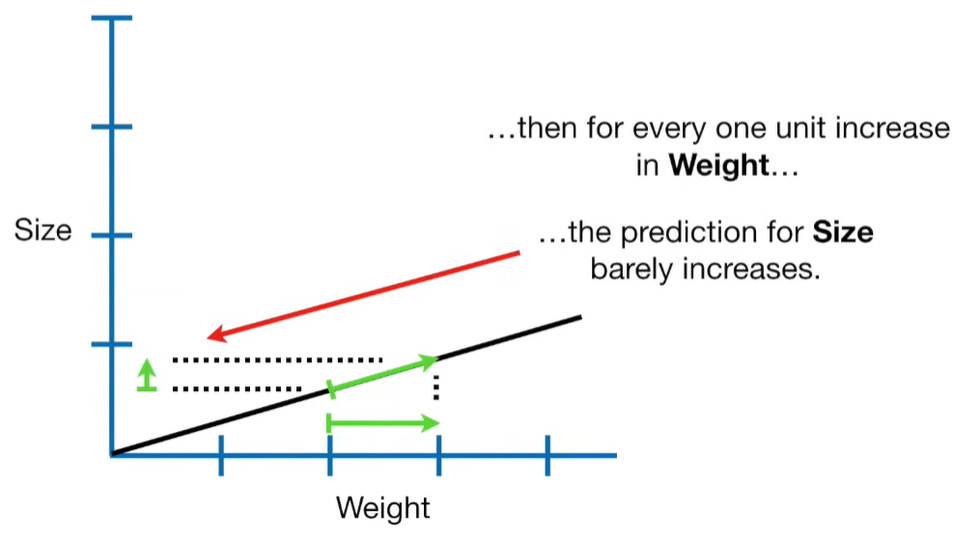
Ridge Regression is a type of linear regression that includes a regularization term to prevent overfitting. It’s particularly useful when dealing with multicollinearity (highly correlated independent variables) or when the number of predictors exceeds the number of observations.

---

🔹 What It Is

Ridge regression is a penalized version of Ordinary Least Squares (OLS) regression. It modifies the loss function used in OLS by adding a penalty term proportional to the square of the magnitude of the coefficients.

---

🔹 How It Works

Standard Linear Regression Loss Function (OLS):

Ridge Regression Loss Function:

 

 

🔹 Key Properties

• Keeps all variables in the model (unlike Lasso regression which can zero some out).

• Particularly effective when predictors are highly correlated.

• Not good for feature selection (since it doesn’t eliminate variables).

---

🔹 Example Use Case

If you're predicting house prices with hundreds of features (square footage, location, age, etc.), Ridge regression helps manage noisy or redundant features without completely discarding them.

---

🔹 When to Use Ridge Regression

• When multicollinearity exists.

• When you want a more stable solution than OLS.

• When prediction accuracy is more important than interpretability.

 

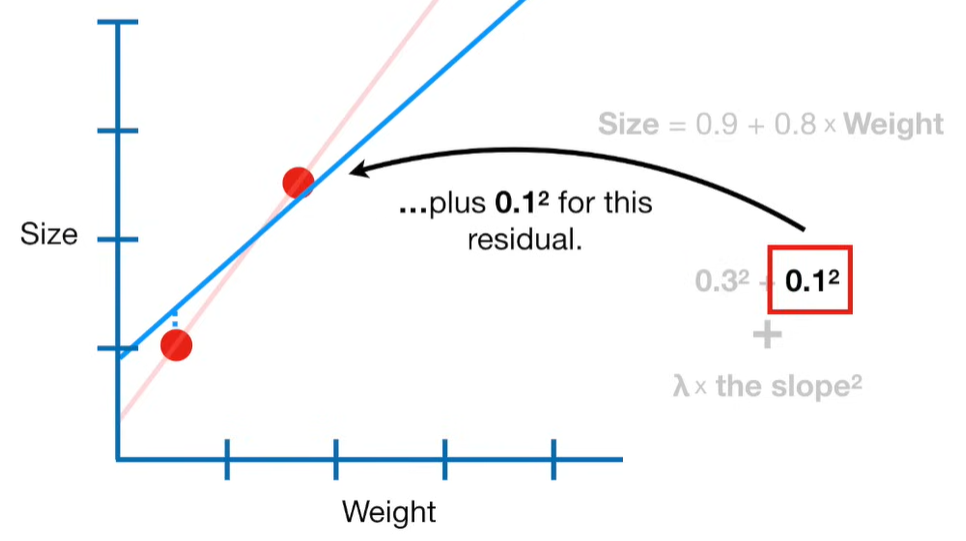
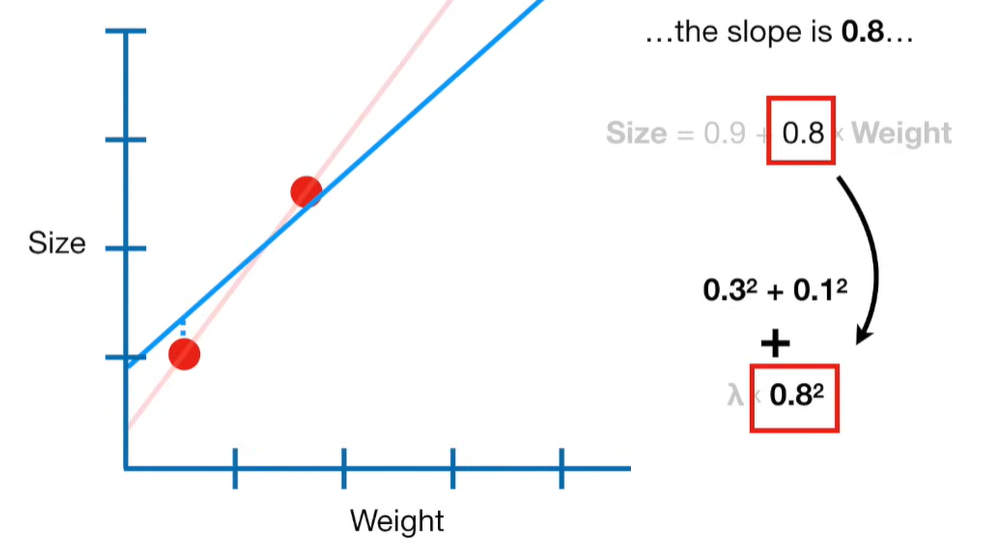
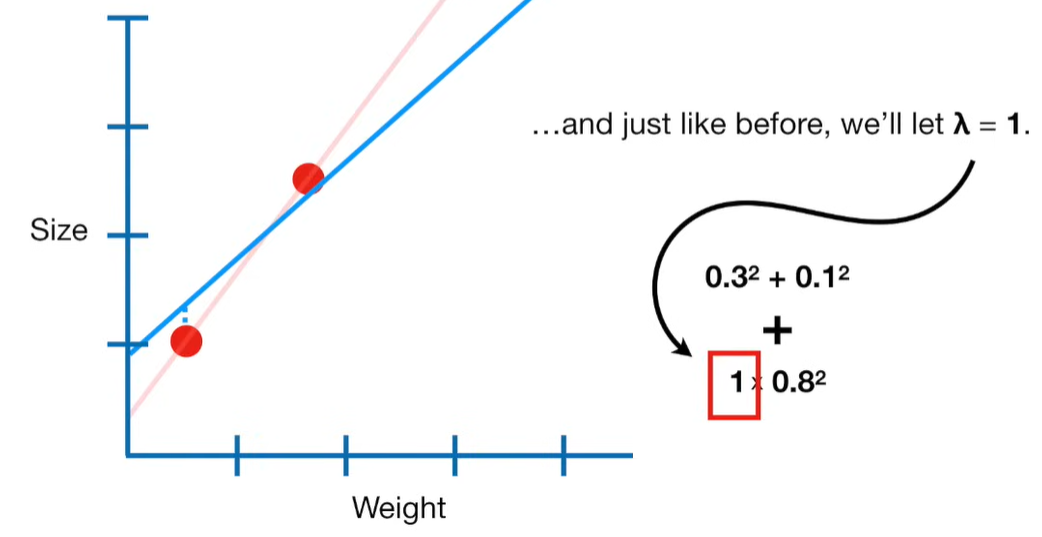
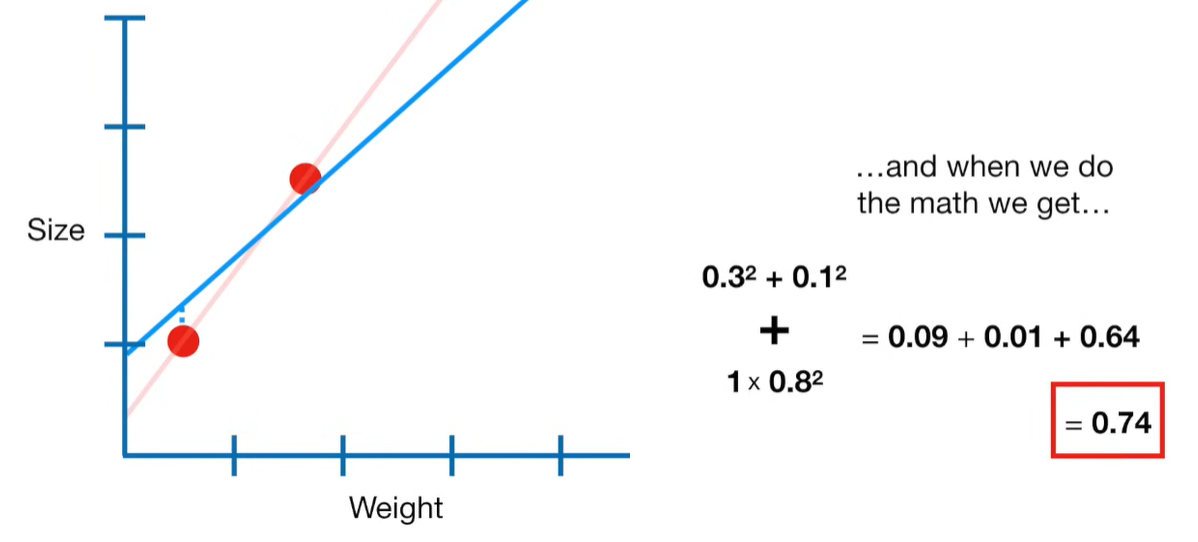
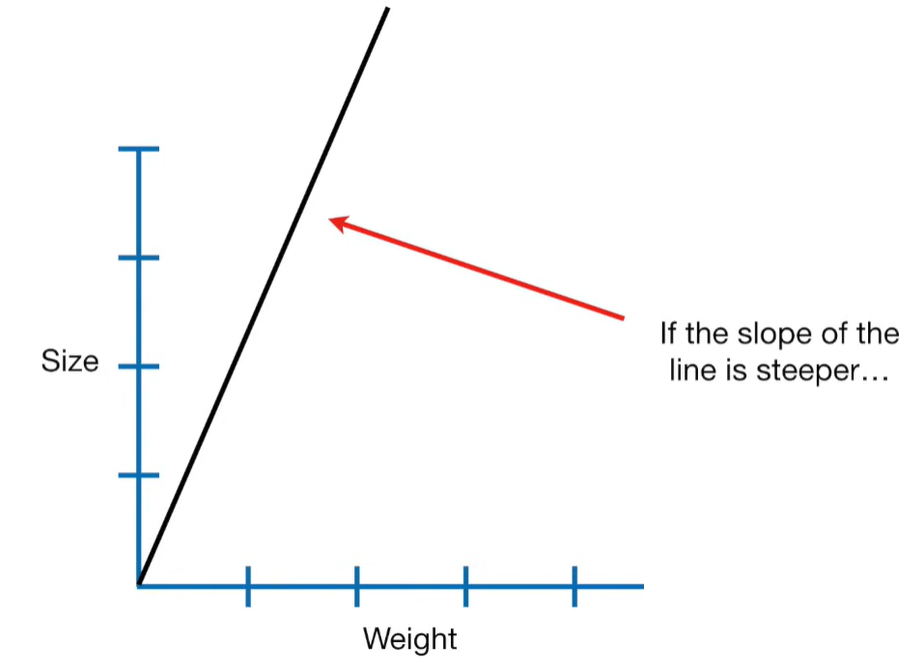
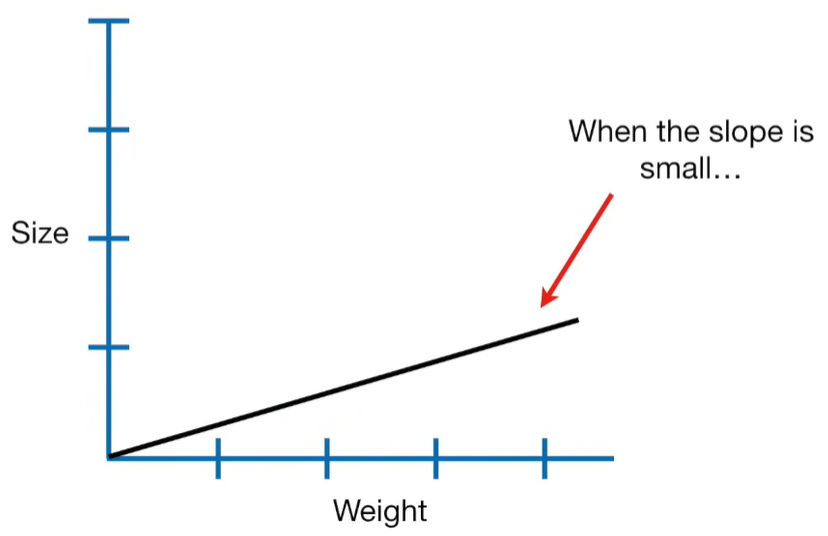
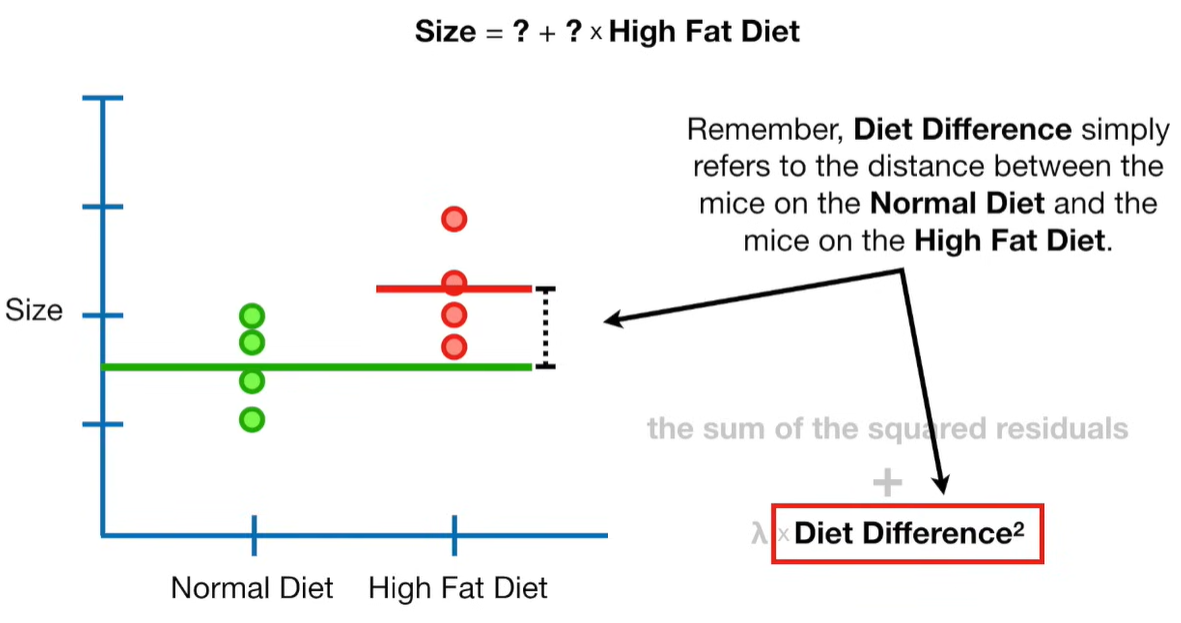
Why can the penalty term can shrink the coefficients toward zero?

 

The penalty term in Ridge regression shrinks the coefficients toward zero because it adds a cost for large coefficient values. Let’s break this down clearly:

---

🔹 Ridge Regression Objective Function

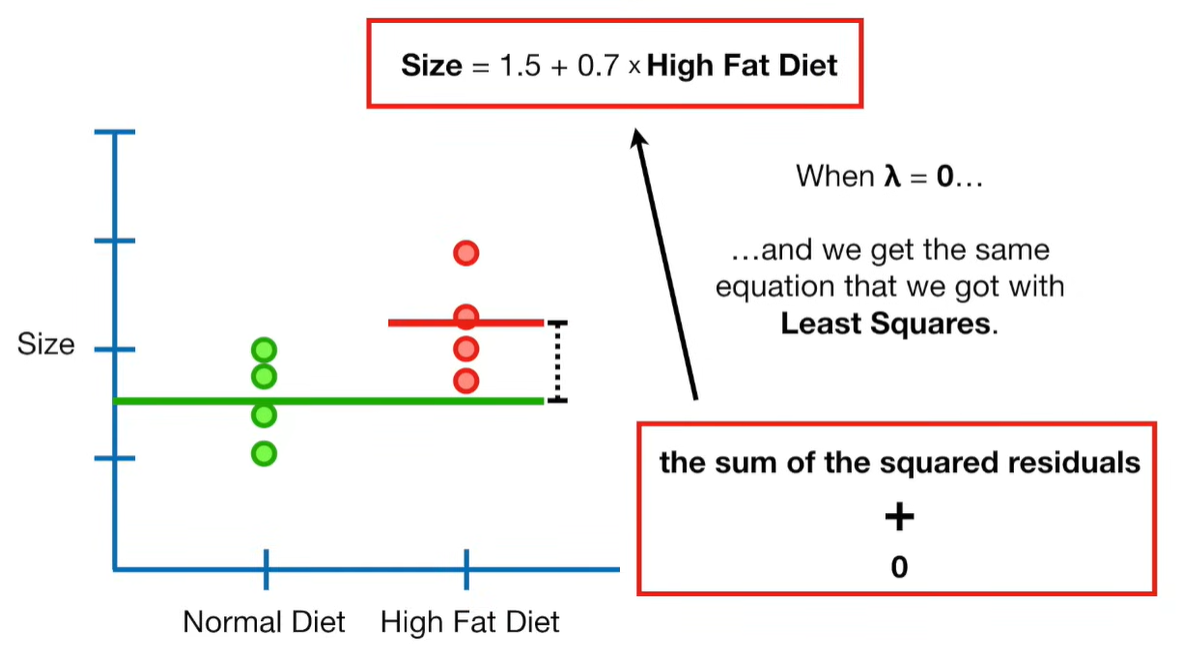
🔹 Why Does This Shrink Coefficients?

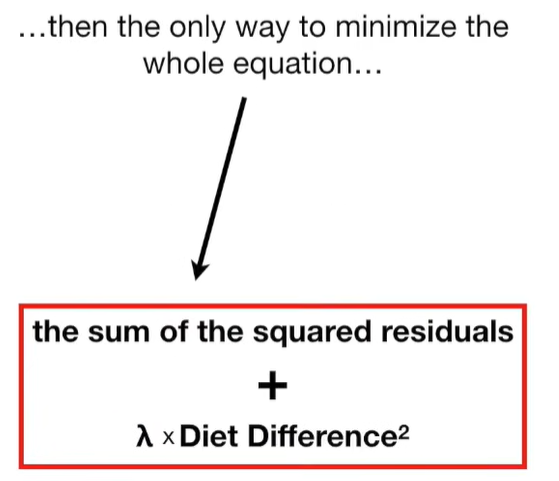
Because the optimizer (e.g. gradient descent or closed-form solution) tries to minimize the total cost, it faces a trade-off:

• Fit the data well (small error term),

• But keep coefficients small (small penalty term).

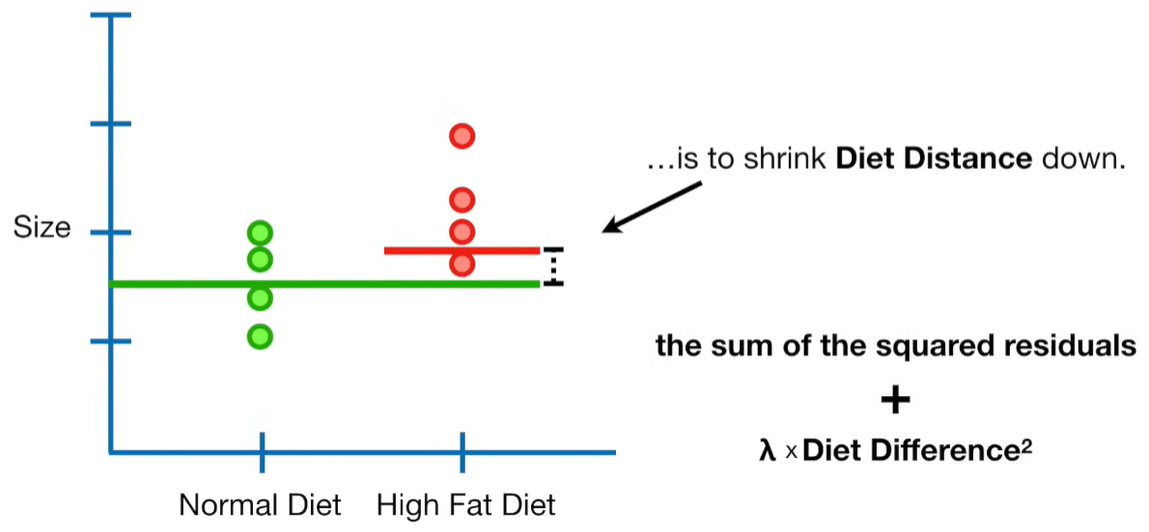
To minimize the total loss, it will often sacrifice some accuracy (allowing a bit more prediction error) in order to reduce the size of the coefficients and keep the penalty term low.

 

 

 

 

     

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

     

 

 

 

 

 

 

 

     

 

 

 

 

 

 

     

 

 

 

 

 

          

 

     

 

     

 

 

 

 

     

 

 

 

 

 

 

     

 

     

 

 

 

 

 

 

 

 

 

 

 

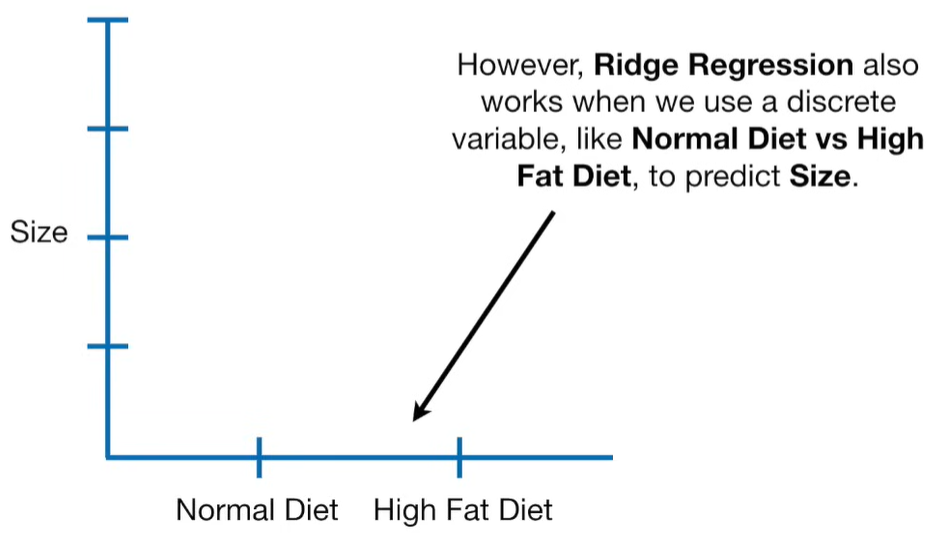
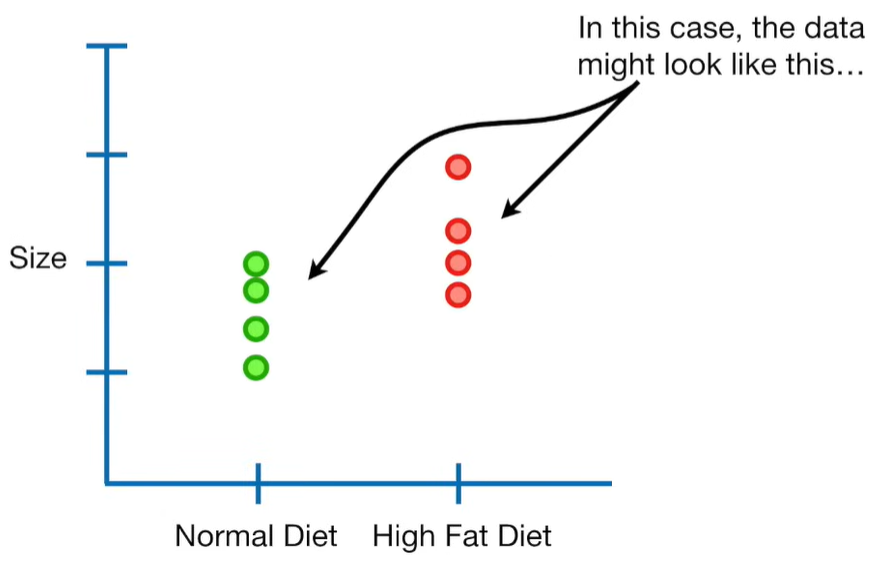
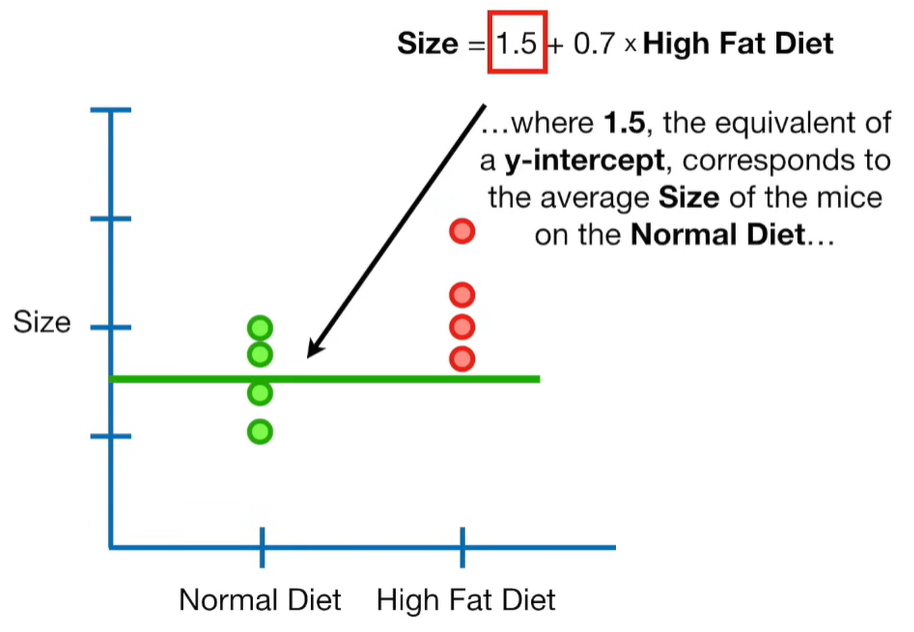
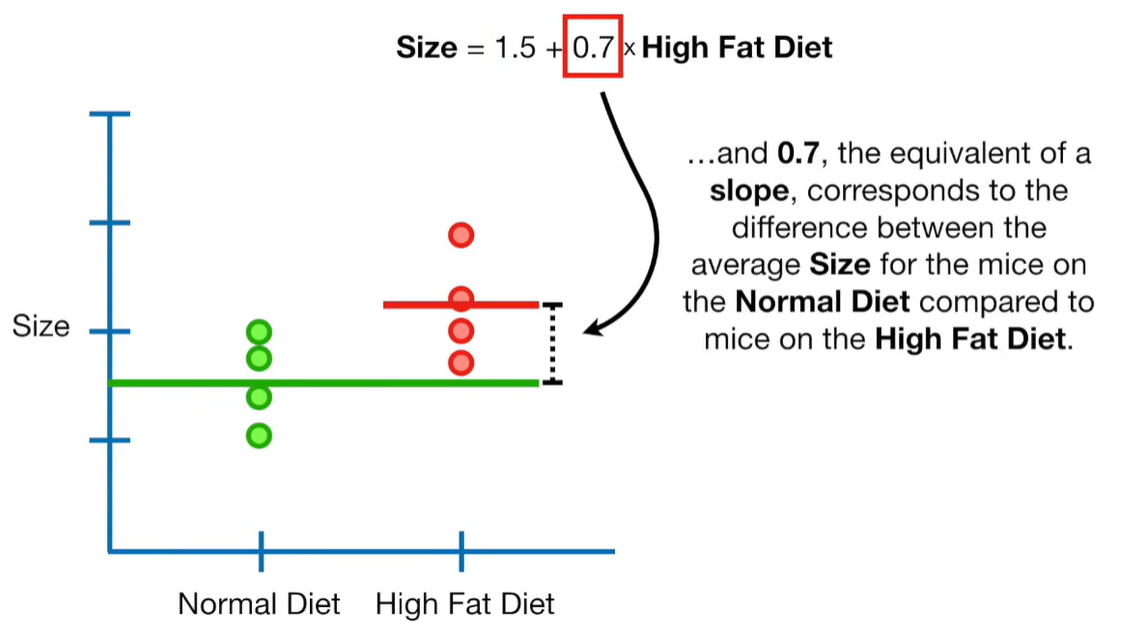
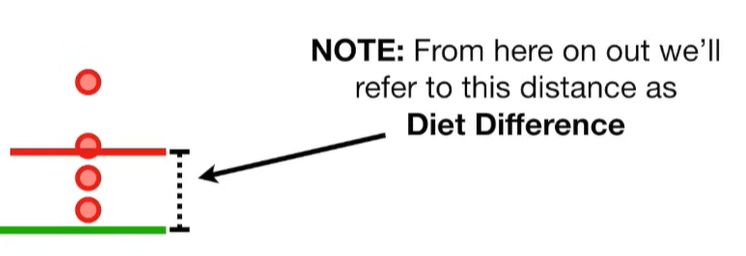
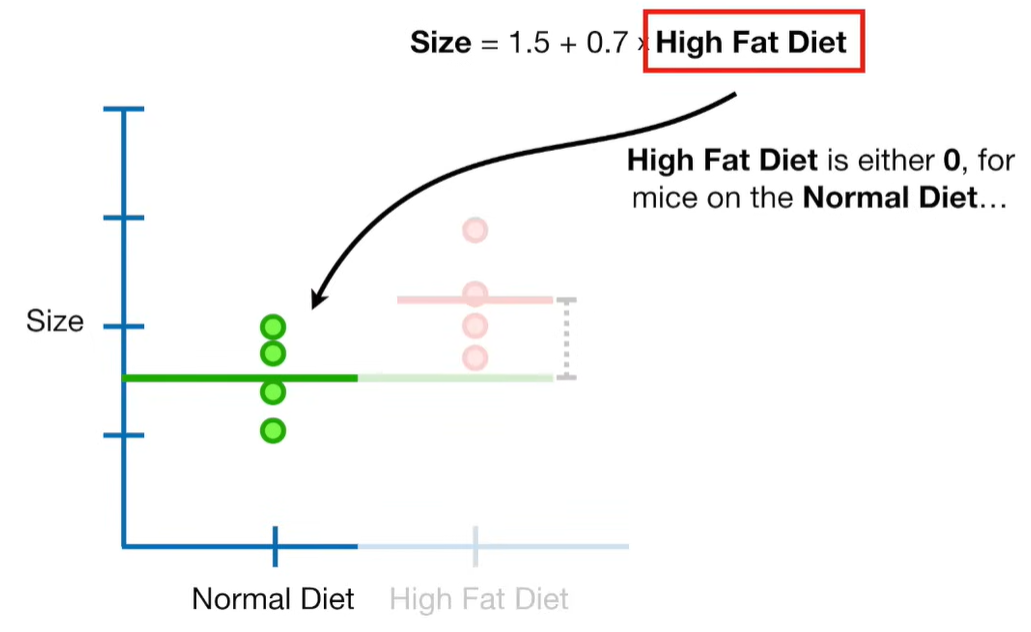
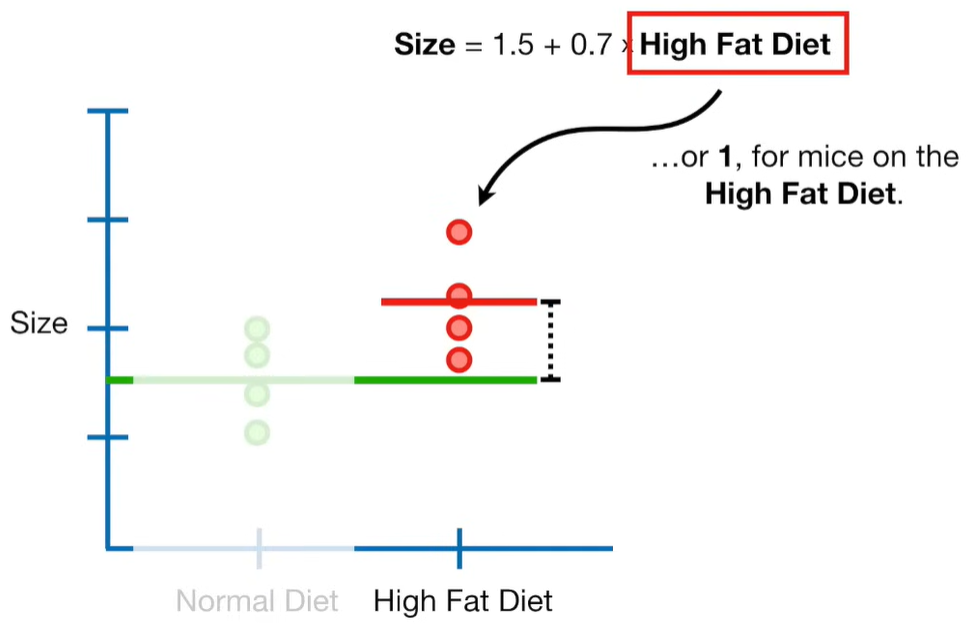
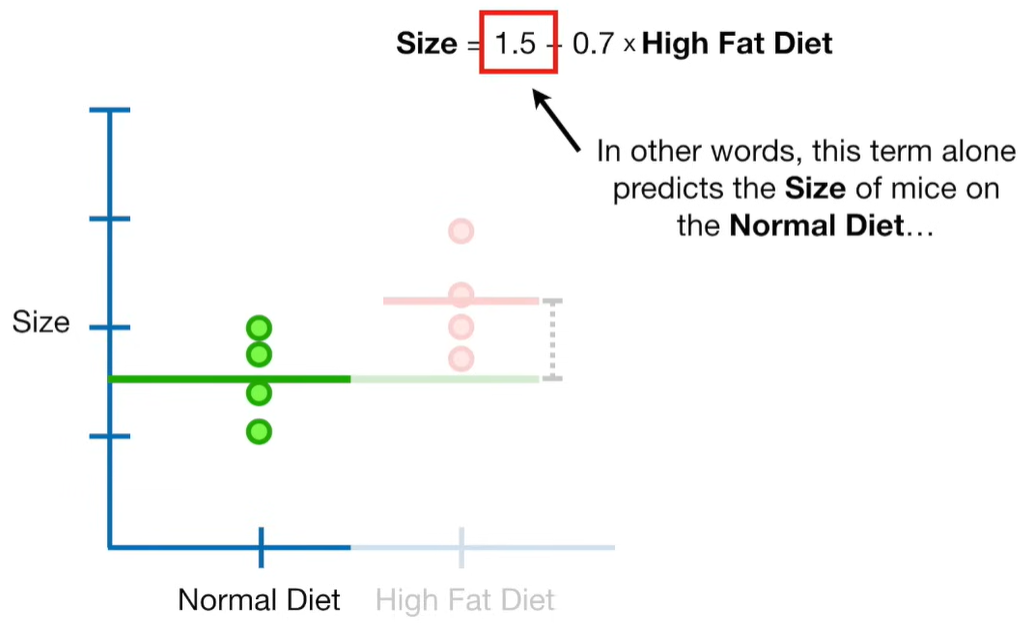
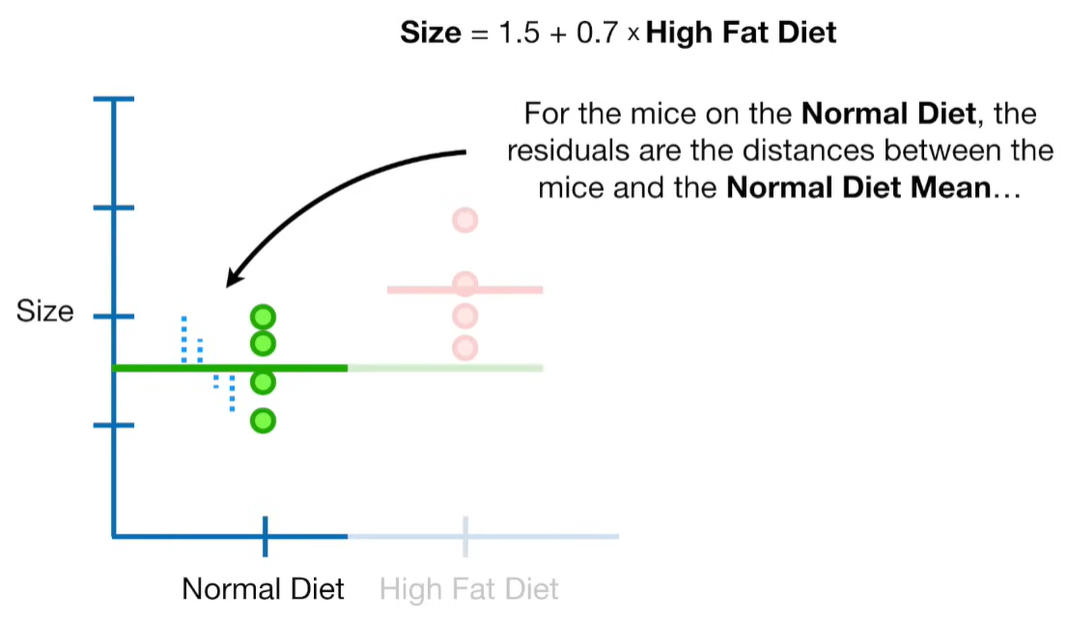
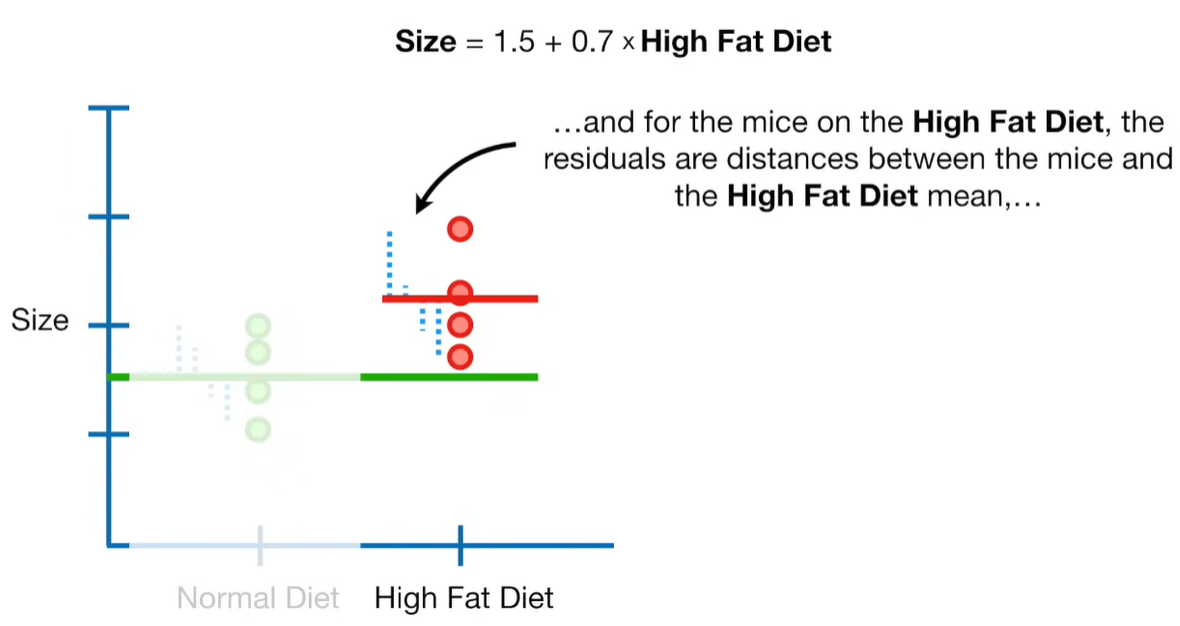
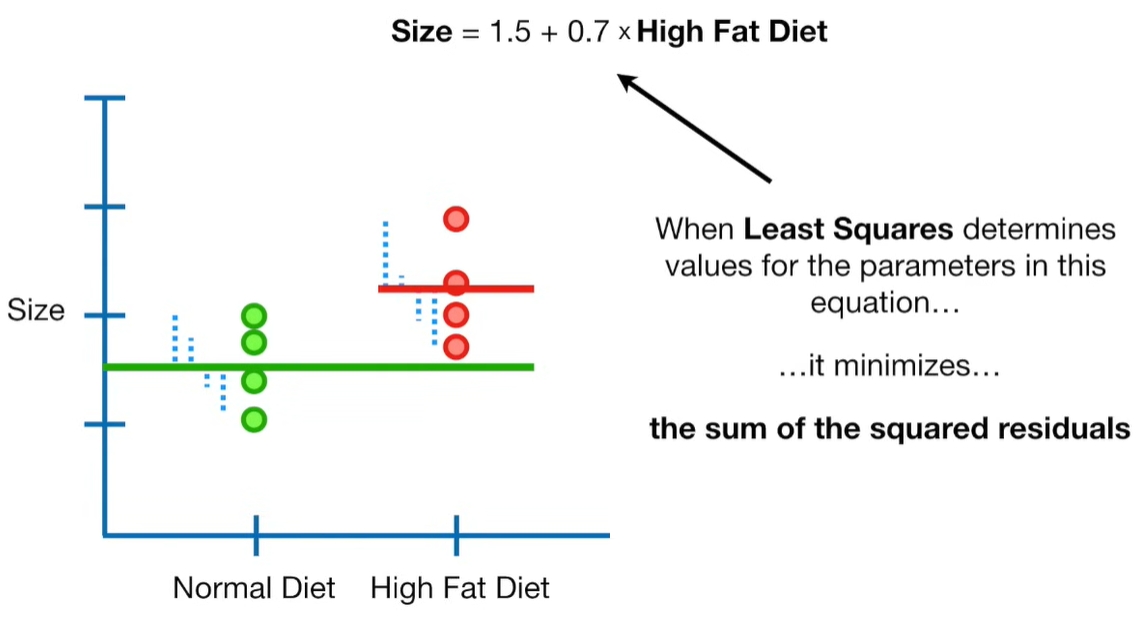
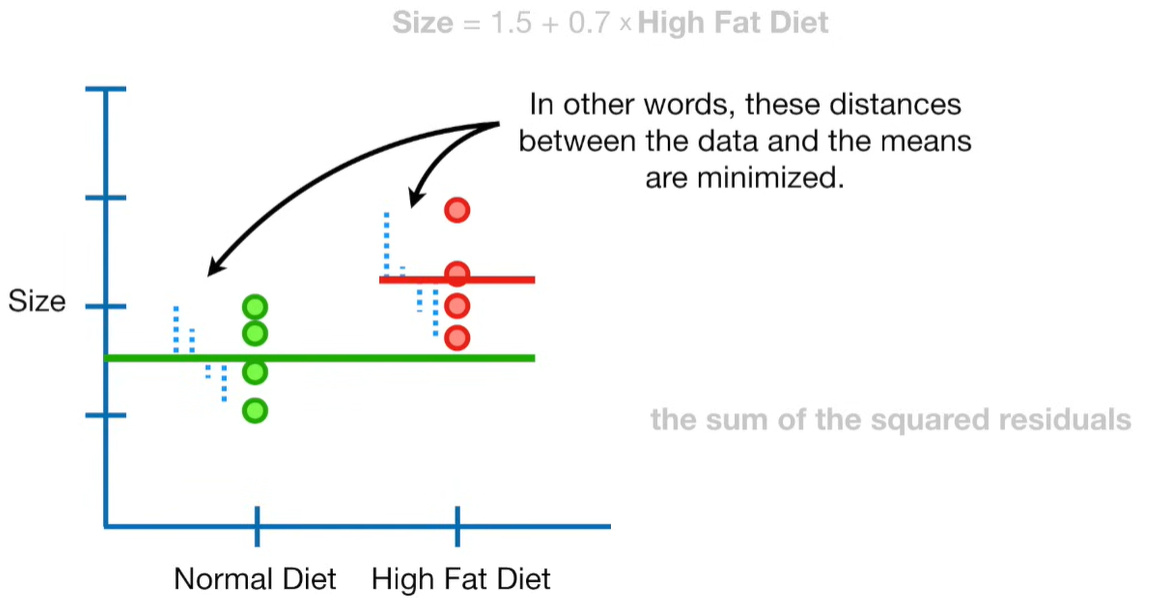
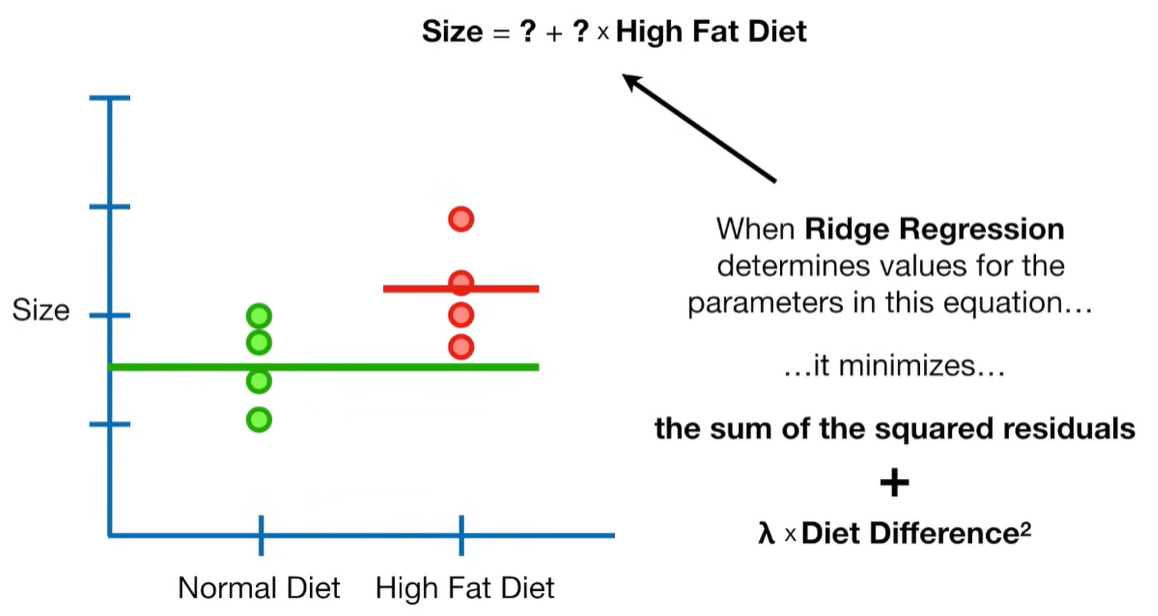
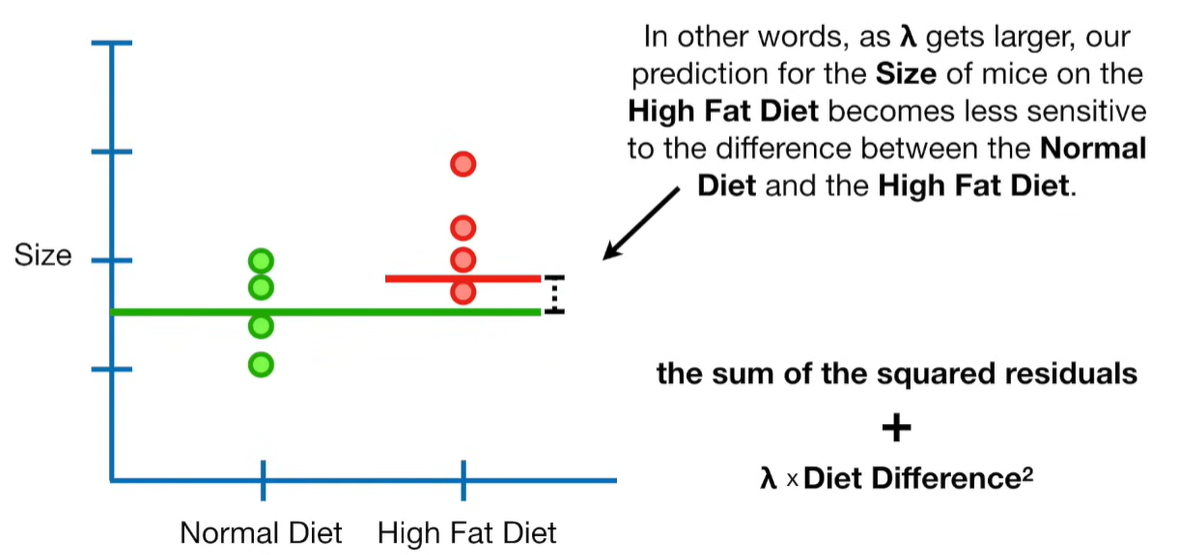
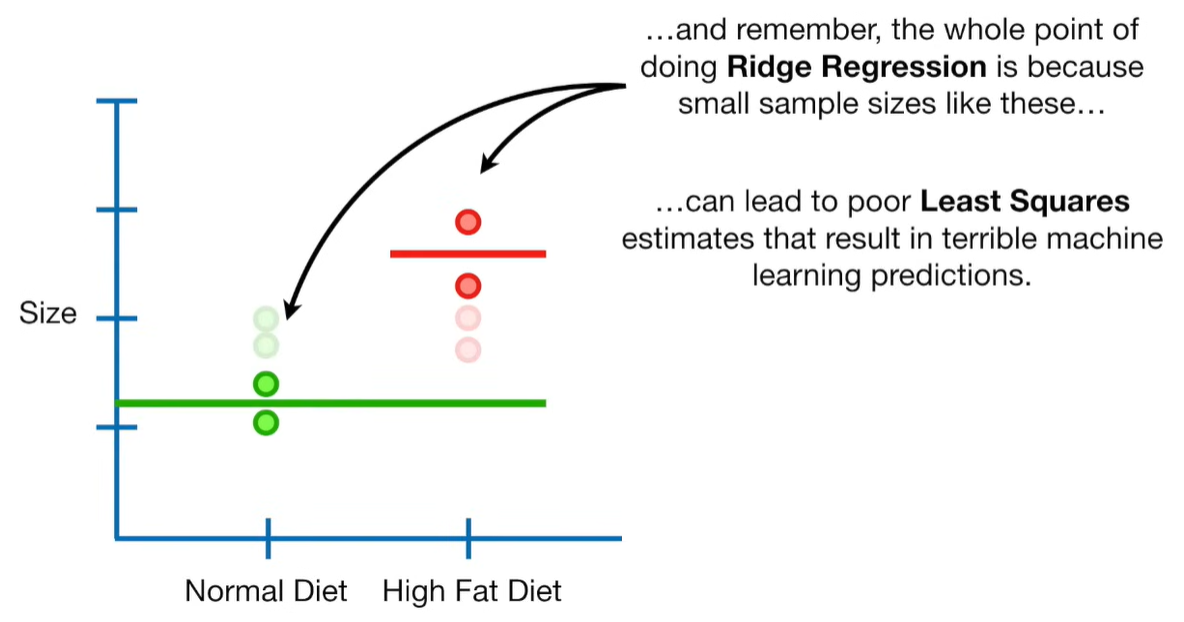
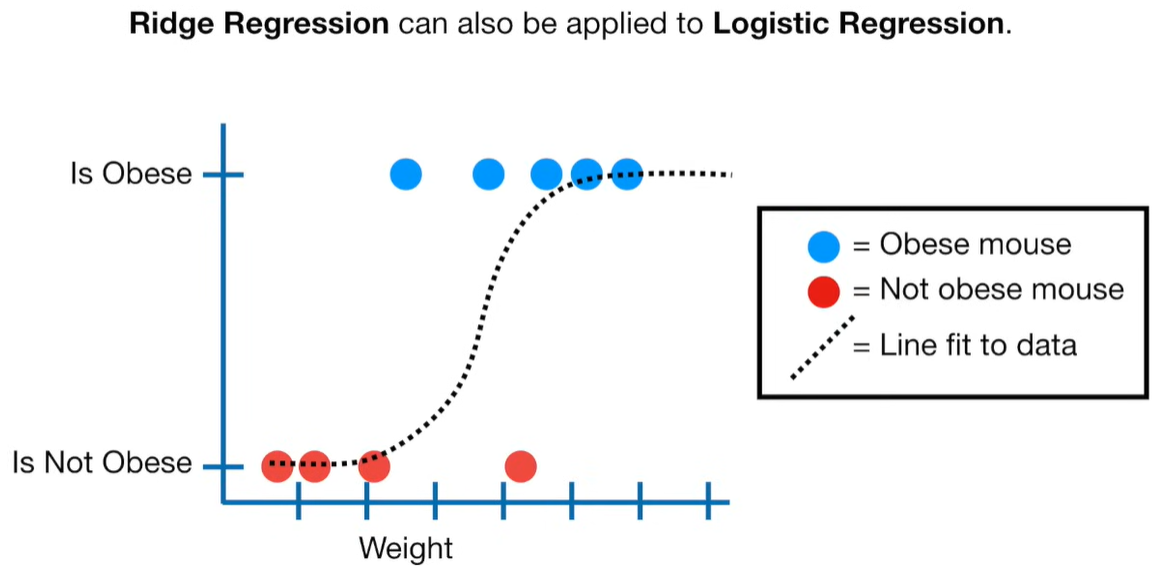
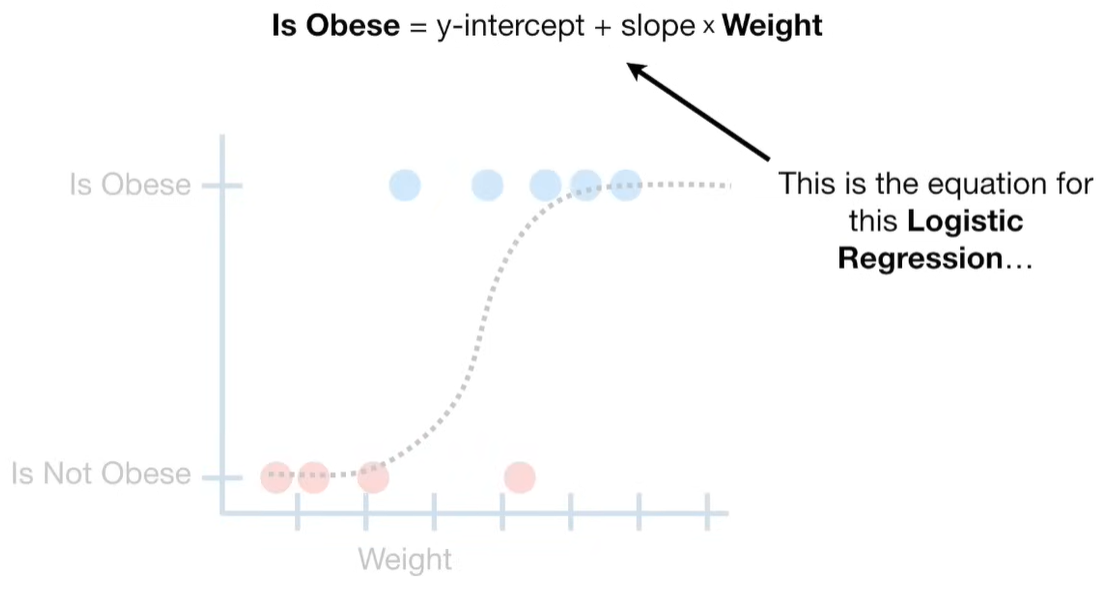
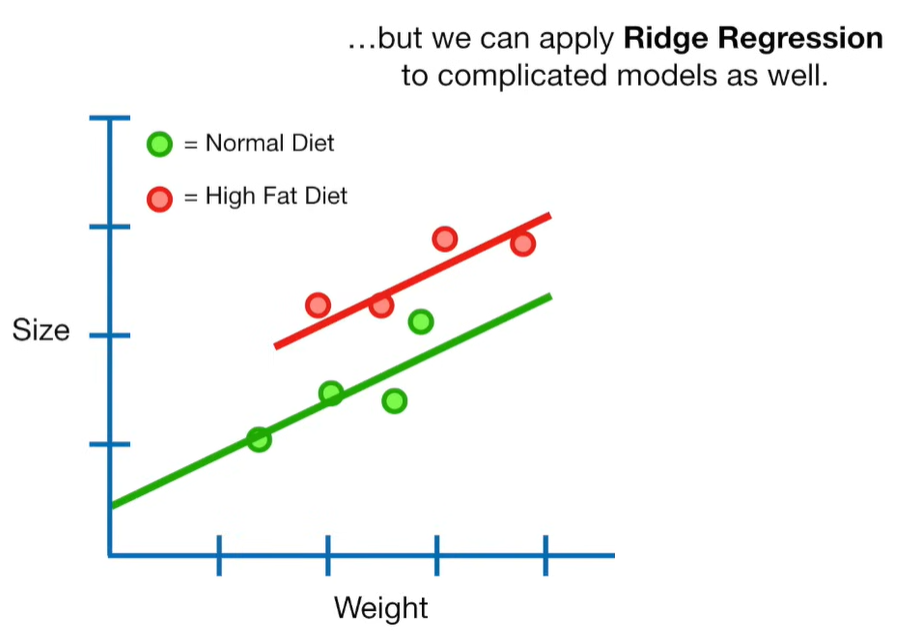
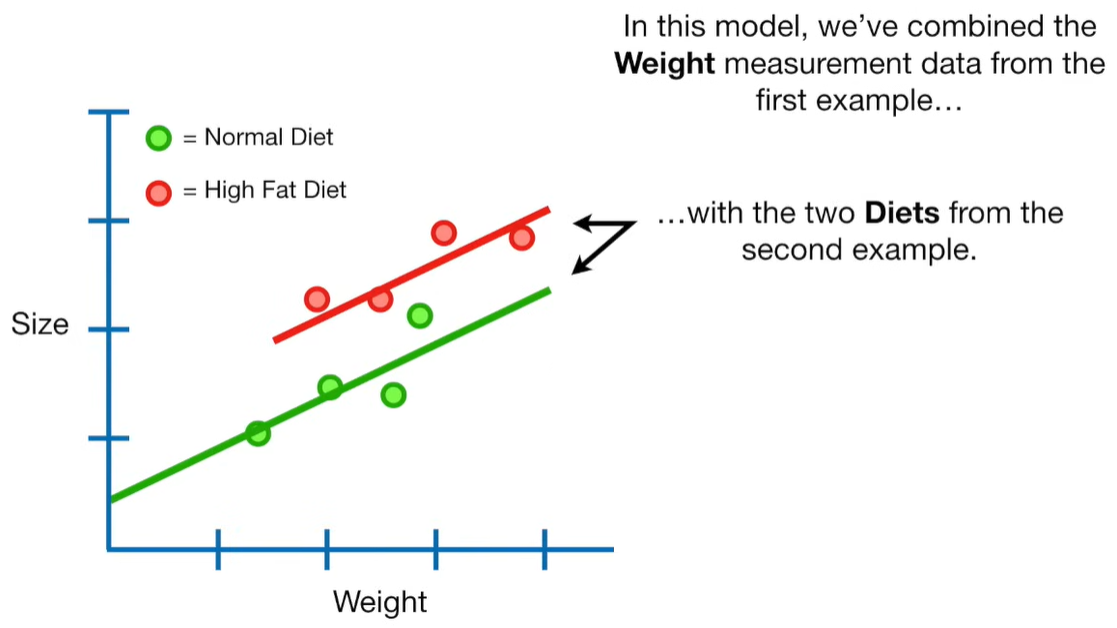
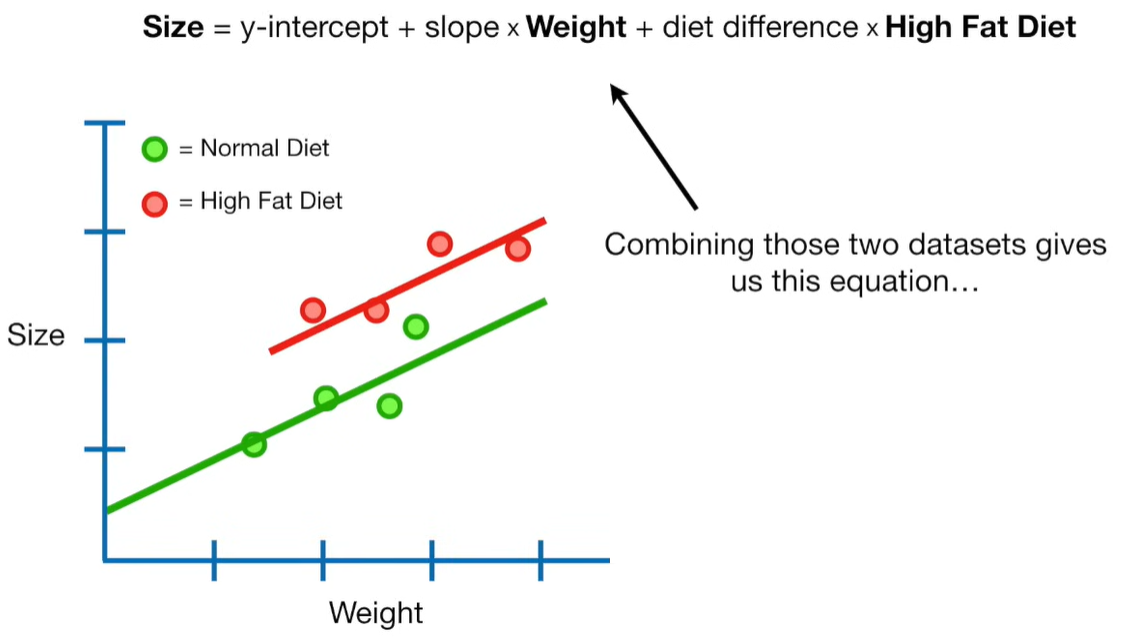
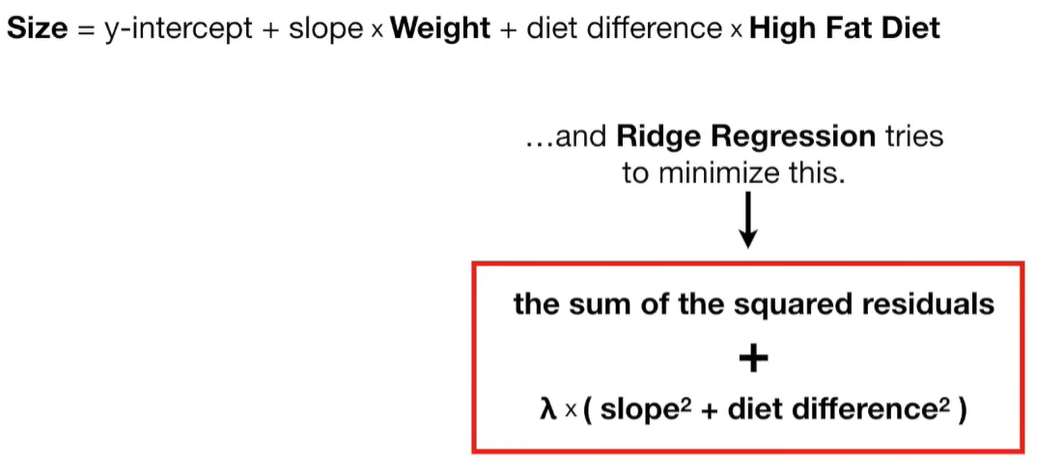
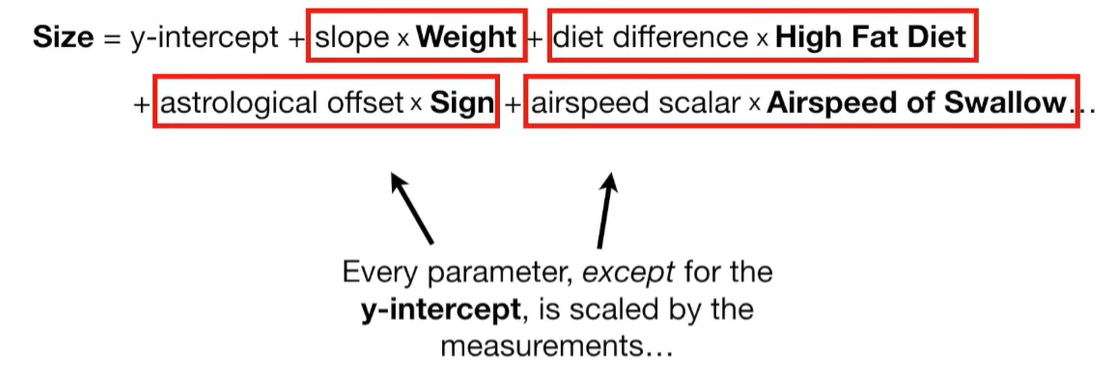
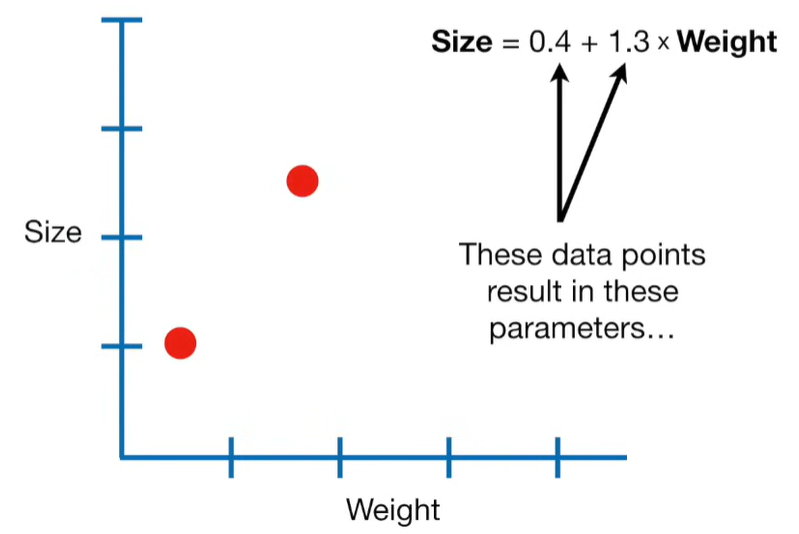
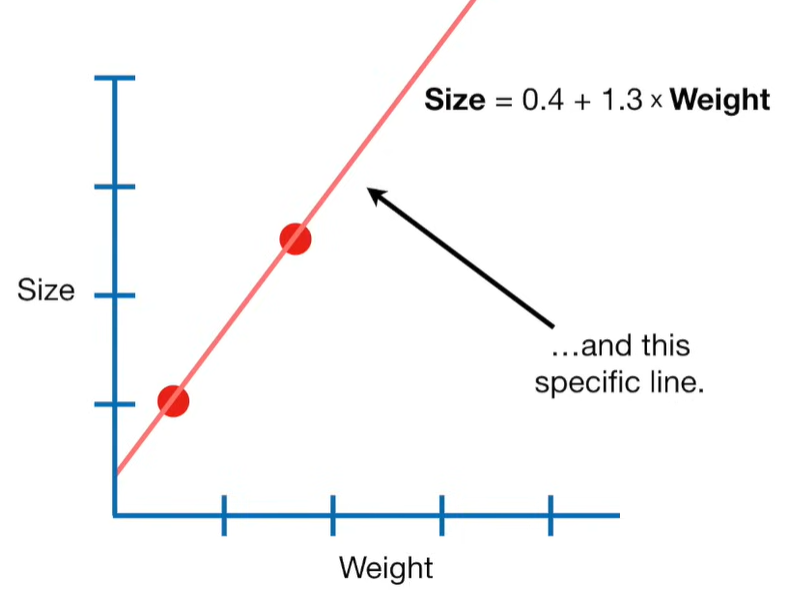
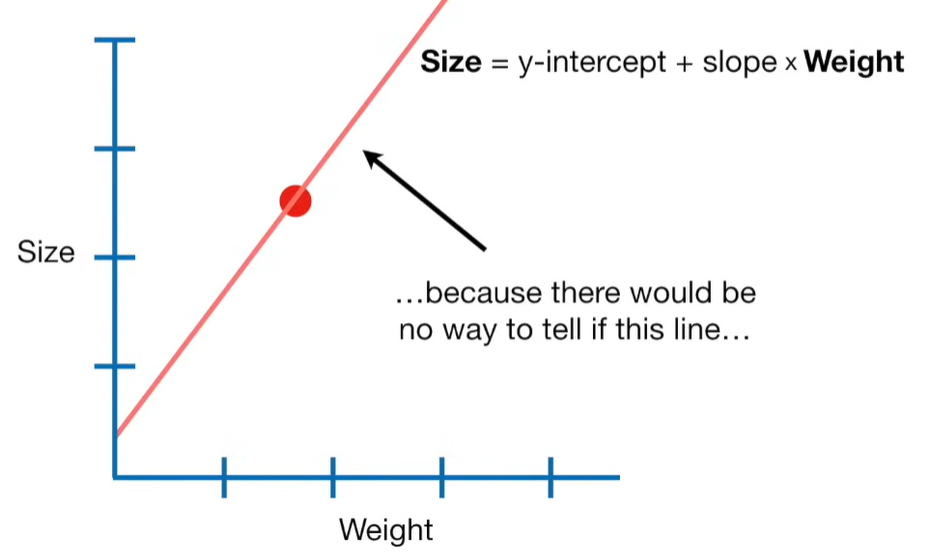
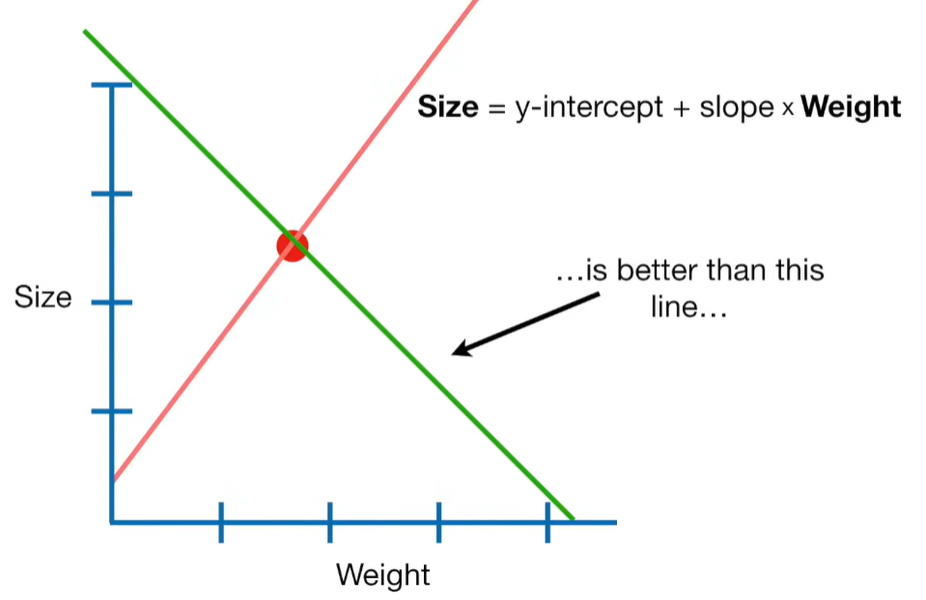
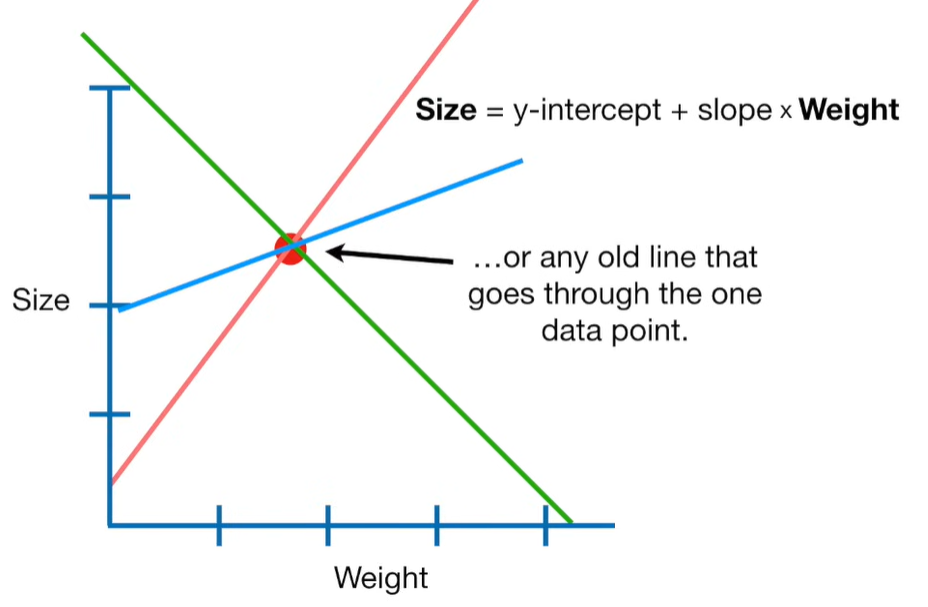
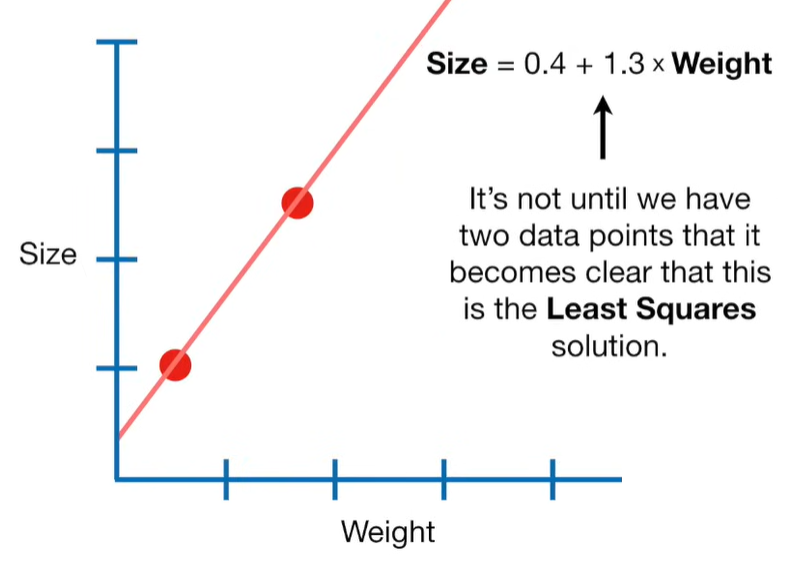
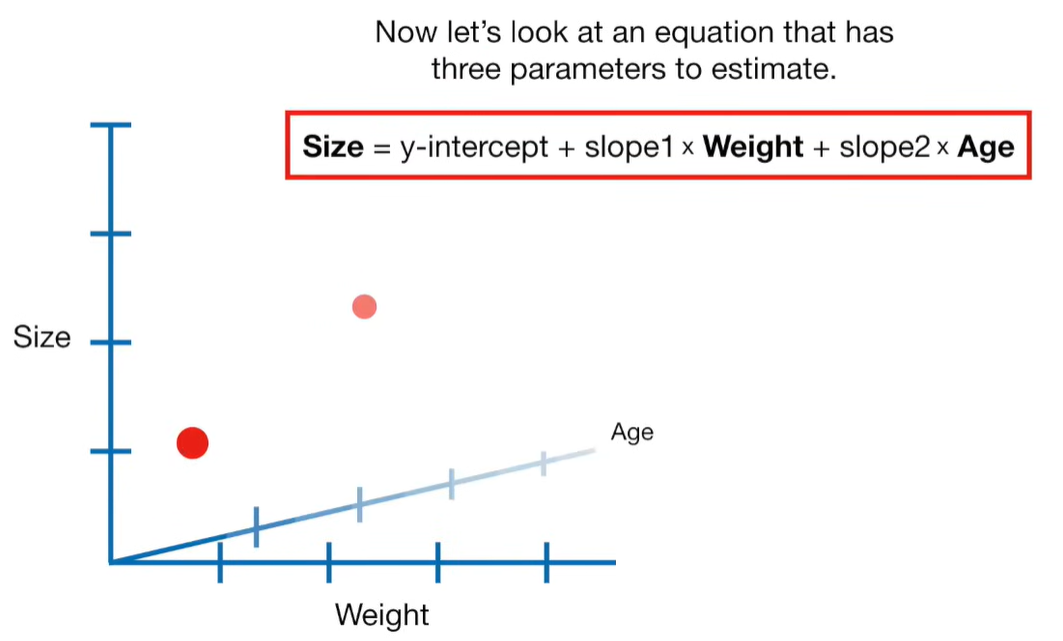
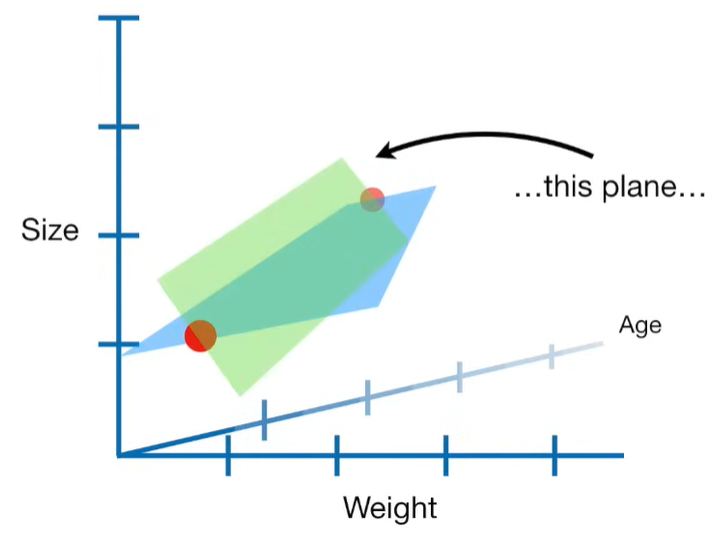
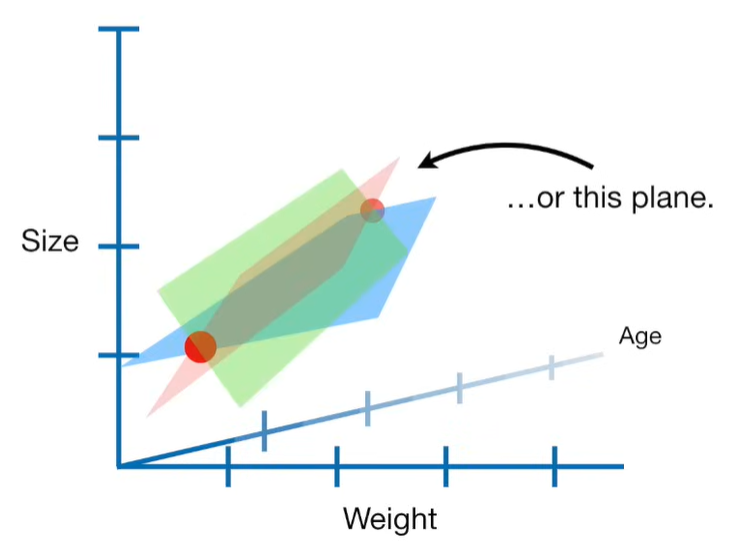
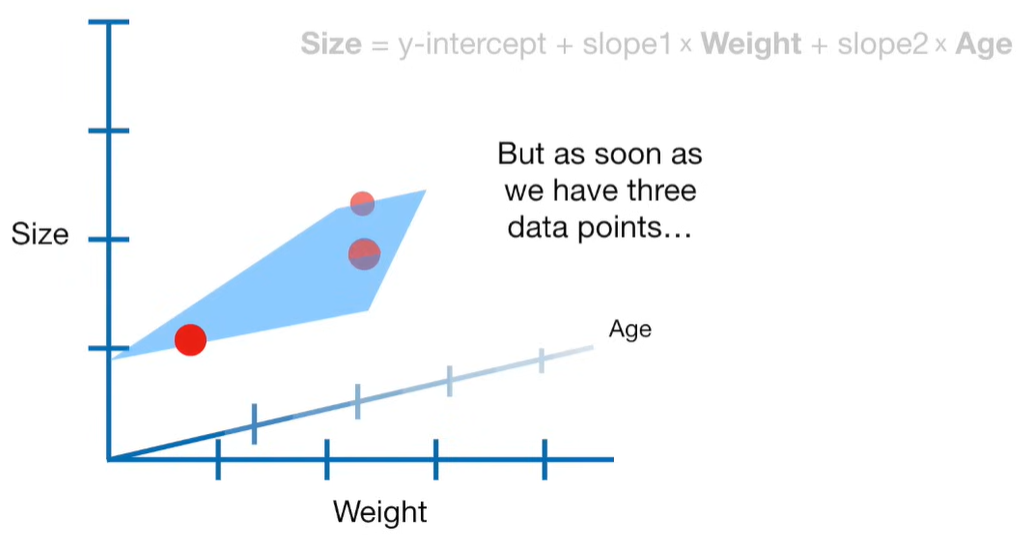
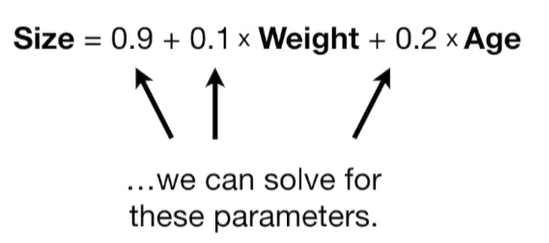
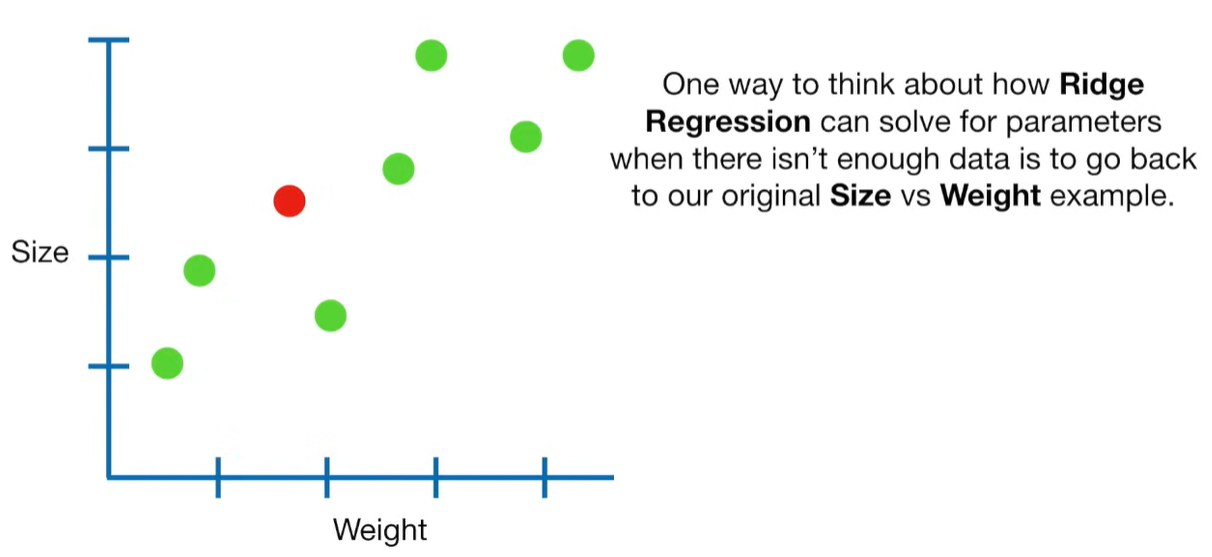
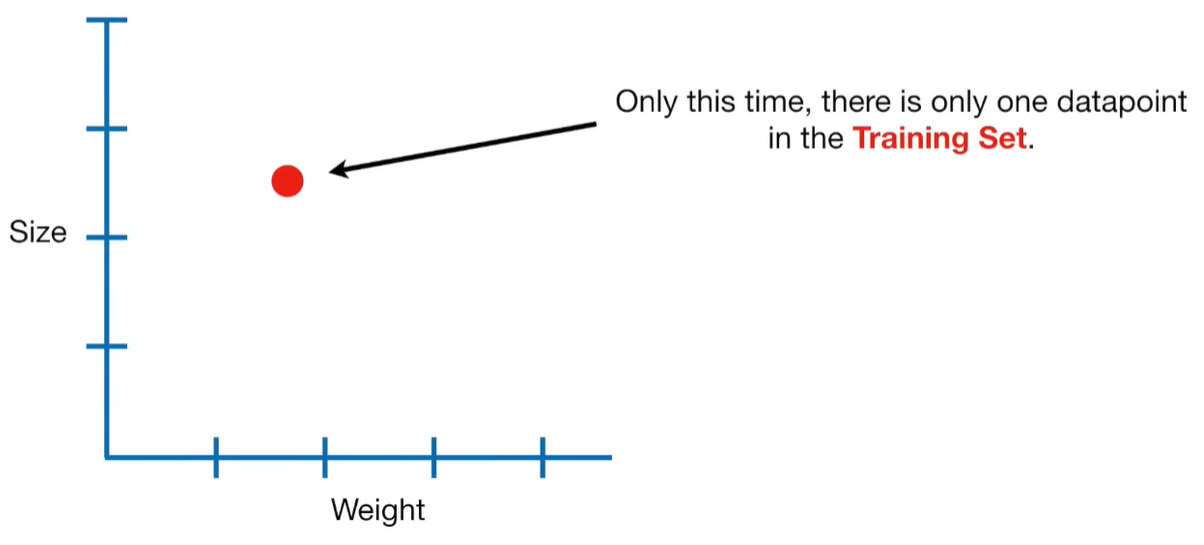
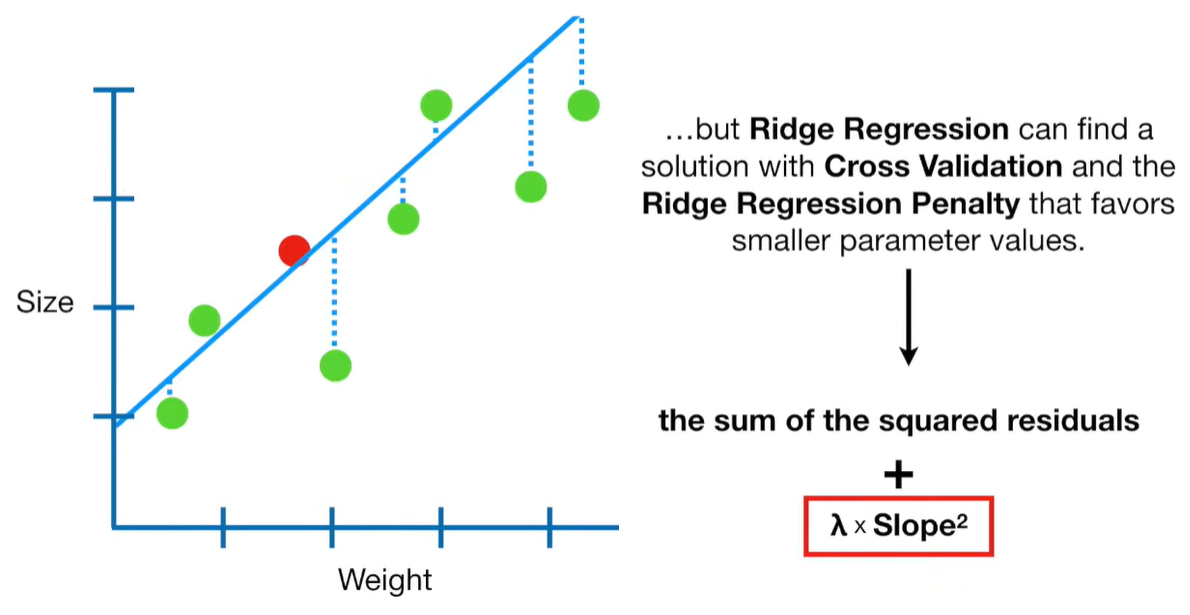
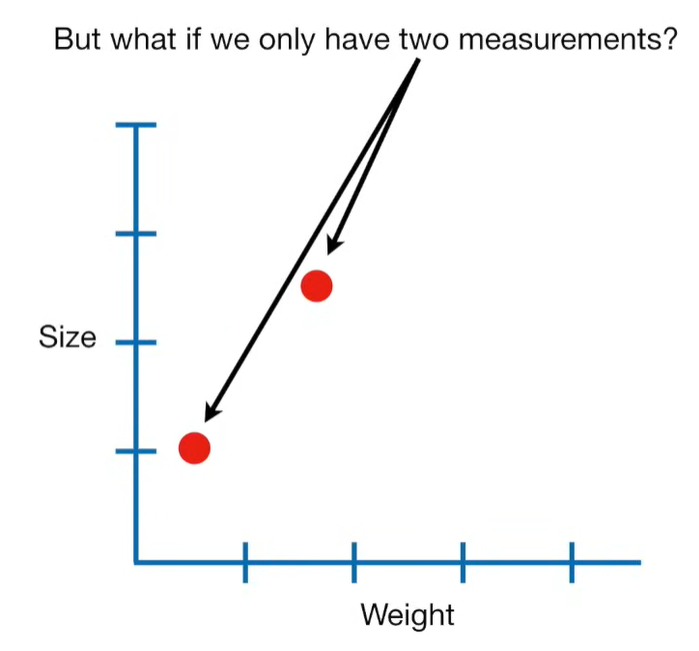
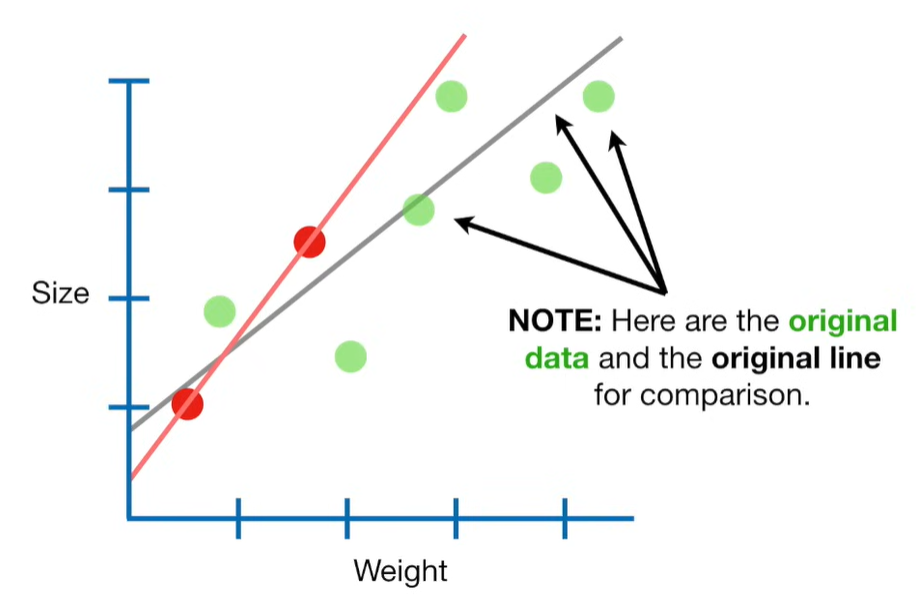
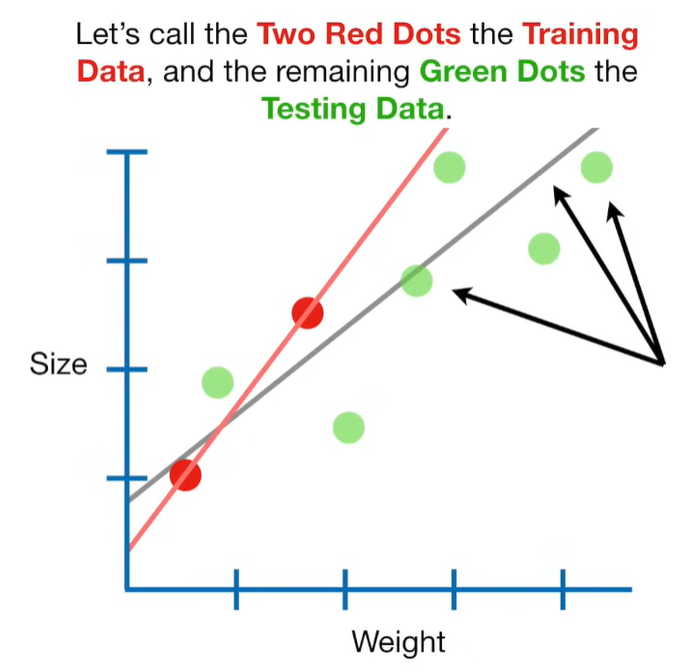
A lot of people ask about 15:34 and how we are supposed to do Cross Validation with only one data point. At this point I was just trying to keep the example simple and if, in practice, you don't have enough data for cross validation then you can't fit a line with ridge regression. However, much more common is that you might have 500 variables but only 400 observations - in this case you have enough data for cross validation and can fit a line with Ridge Regression, but since there are more variables than observations, you can't do ordinary least squares.