Machine Learning - Using Linear Models for t-tests and ANOVA

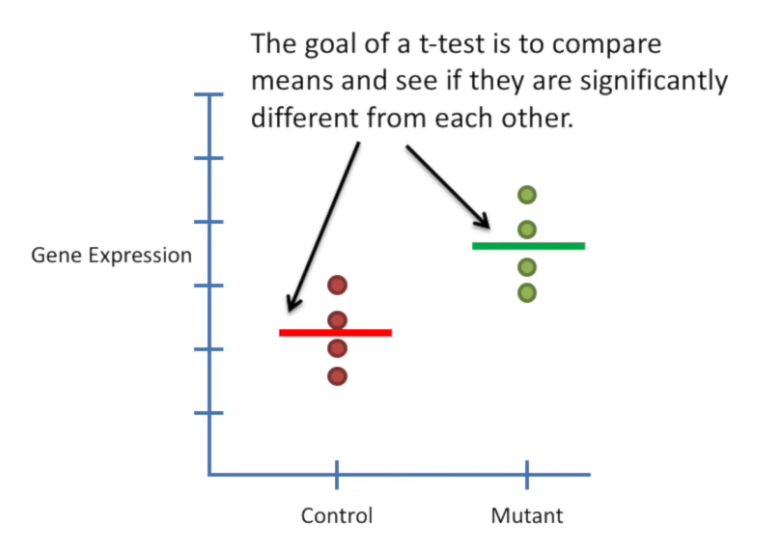
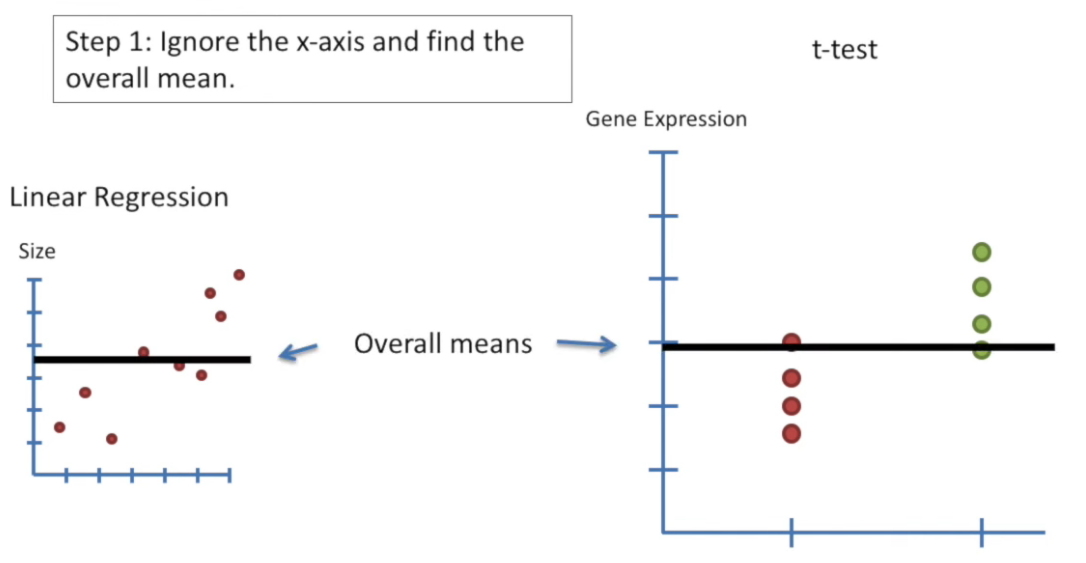
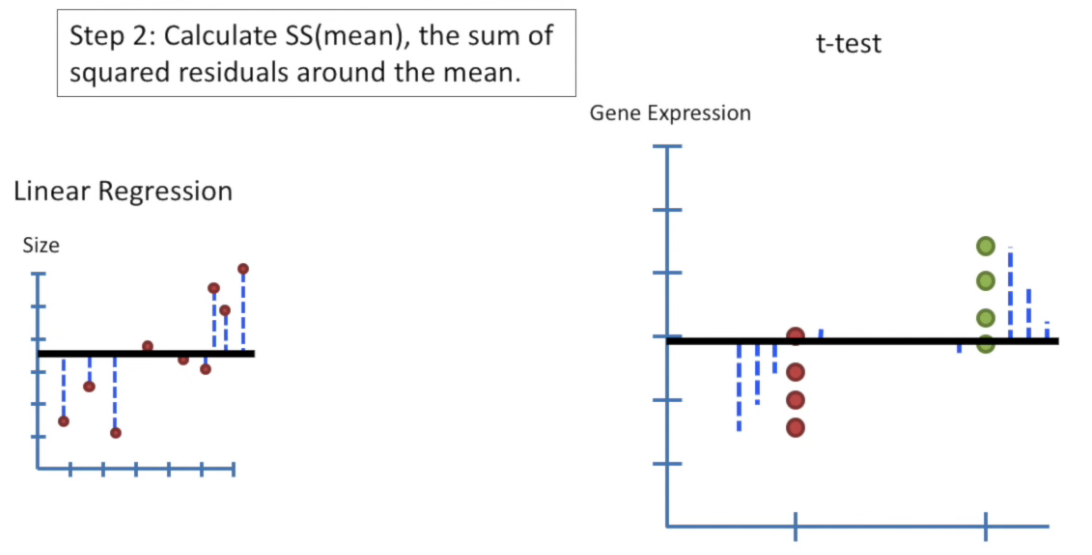
A t-test is a statistical test used to determine whether there is a significant difference between the means of two groups. It helps answer questions like:

“Are these two groups really different, or is the difference just due to random chance?”

---

🎯 Purpose of the t-test

To compare two means and test the null hypothesis:

• H₀ (null): The two population means are equal.

• H₁ (alternative): The two population means are not equal.

---

📊 Types of t-tests

Type	When to Use
One-sample t-test	Compare the sample mean to a known value (e.g., test score vs. national average).
Two-sample (independent) t-test	Compare means of two independent groups (e.g., males vs. females).
Paired t-test	Compare two related samples (e.g., before and after treatment on the same subjects).

 

 

✅ Example

Suppose you want to compare the average test scores of two classes:

• Class A scores: [85, 87, 90, 92]

• Class B scores: [78, 80, 83, 85]

You can use a two-sample t-test to check if the difference in average scores is statistically significant.

 

import numpy as np
from scipy.stats import ttest_ind


# Sample data
class_A = [85, 87, 90, 92]
class_B = [78, 80, 83, 85]

# Perform two-sample t-test (equal variances assumed)
t_stat, p_value = ttest_ind(class_A, class_B)

print(f"t-statistic: {t_stat:.4f}")
print(f"p-value: {p_value:.4f}")

 Interpret the results

If p-value < 0.05, you can reject the null hypothesis and say there's a significant difference between the groups.

Example output might be:

t-statistic: 4.2426
p-value: 0.0025

✅ Conclusion: Since p-value < 0.05, there's a statistically significant difference between Class A and Class B's scores.

 

🧠 Optional: Use equal_var=False if variances are not assumed to be equal (Welch's t-test)

ttest_ind(class_A, class_B, equal_var=False)

 

 

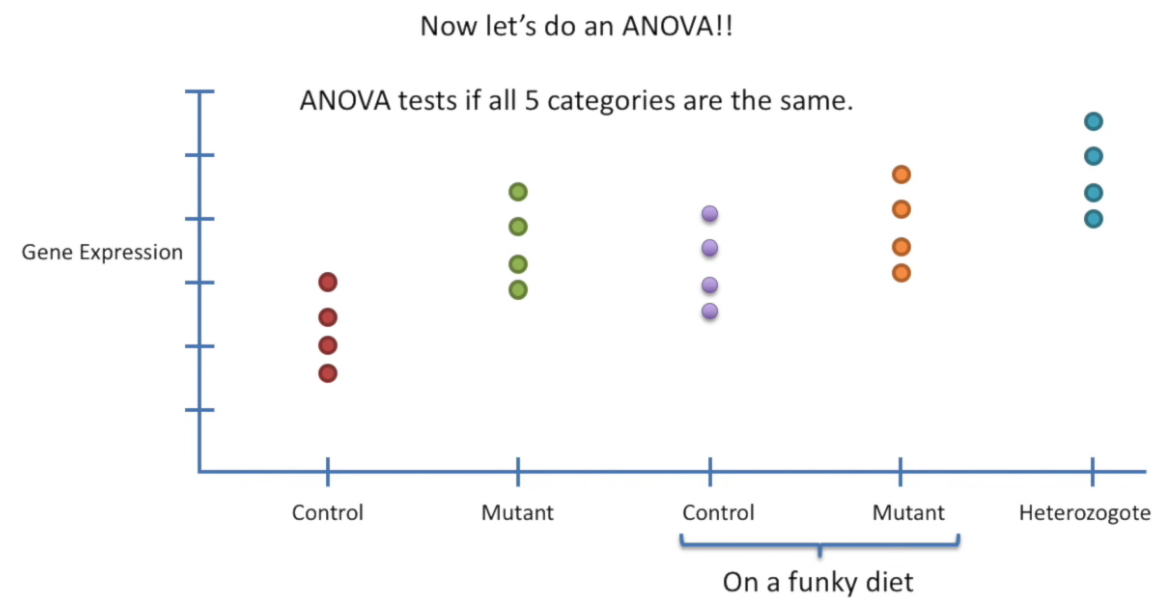
ANOVA stands for Analysis of Variance. It is a statistical method used to determine whether there are any statistically significant differences between the means of three or more independent (unrelated) groups.

---

🔍 Purpose of ANOVA

To test the hypothesis:

• Null Hypothesis (H₀): All group means are equal.

• Alternative Hypothesis (H₁): At least one group mean is different.

---

🧪 When to Use ANOVA

Use ANOVA when:

• You have more than two groups to compare.

• The dependent variable is continuous (e.g., height, weight, score).

• The independent variable(s) are categorical (e.g., group, treatment).

---

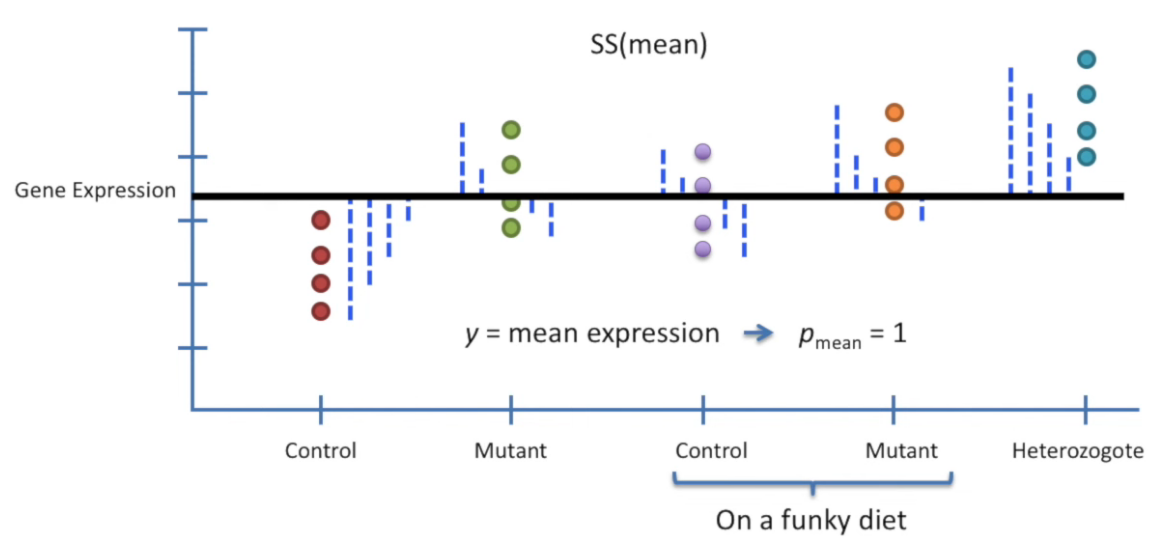
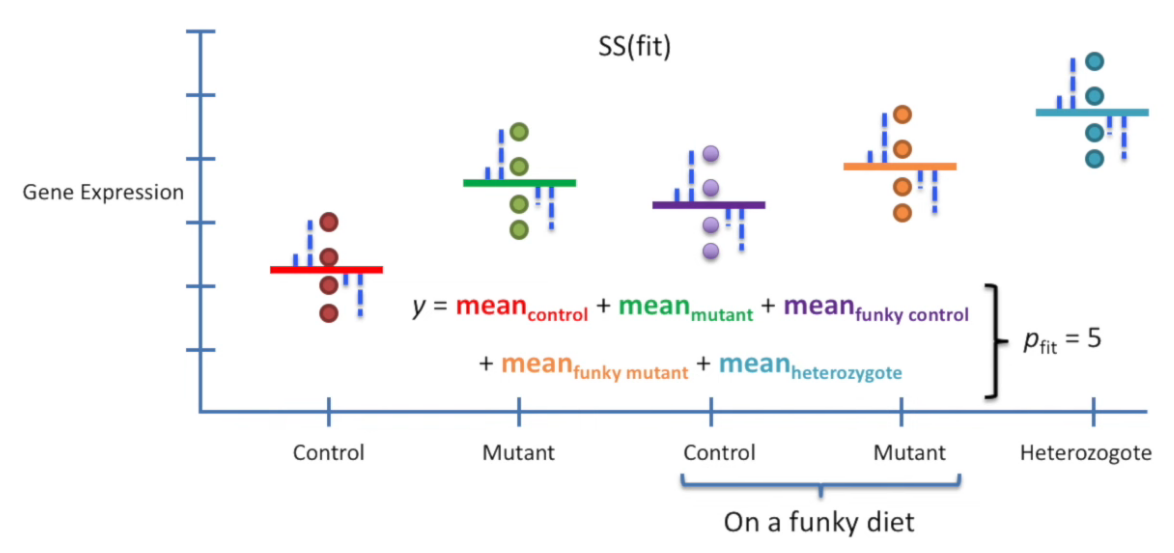
🔢 How ANOVA Works

ANOVA compares:

• Between-group variability: How much the group means vary from the overall mean.

• Within-group variability: How much individual observations vary within each group.

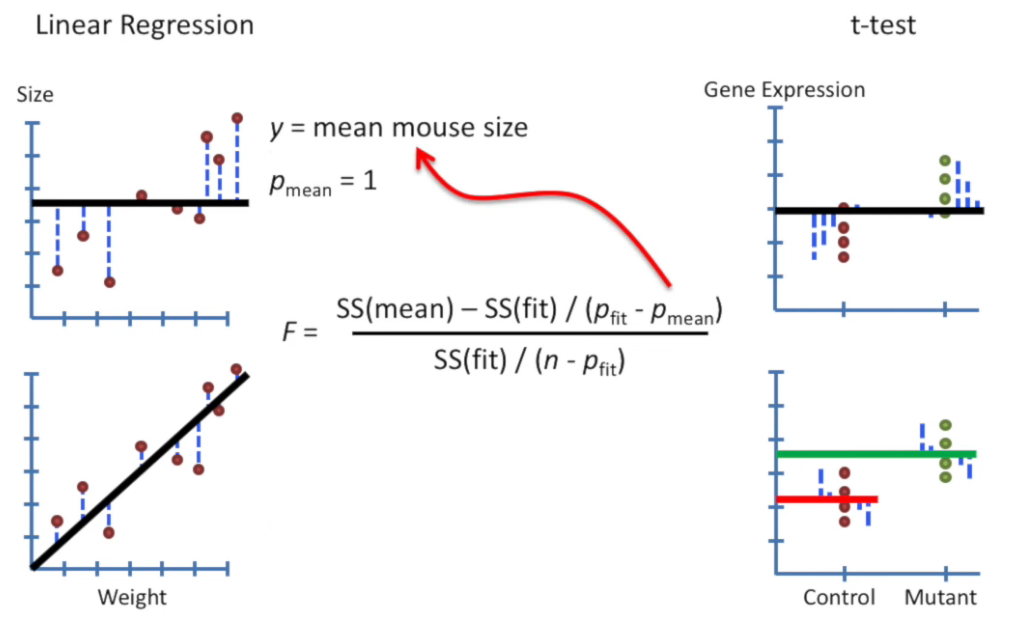
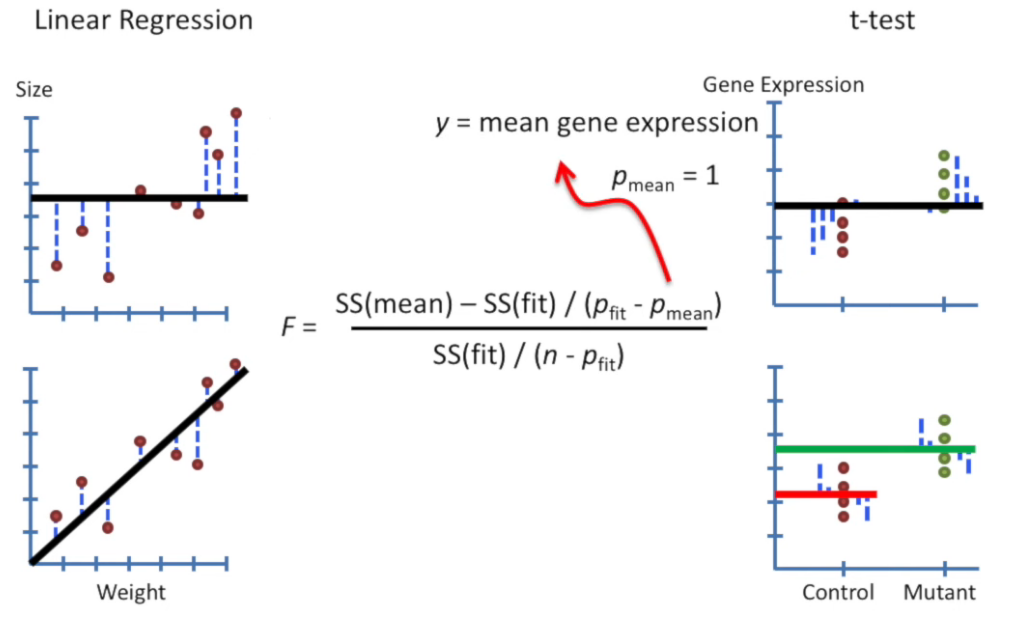
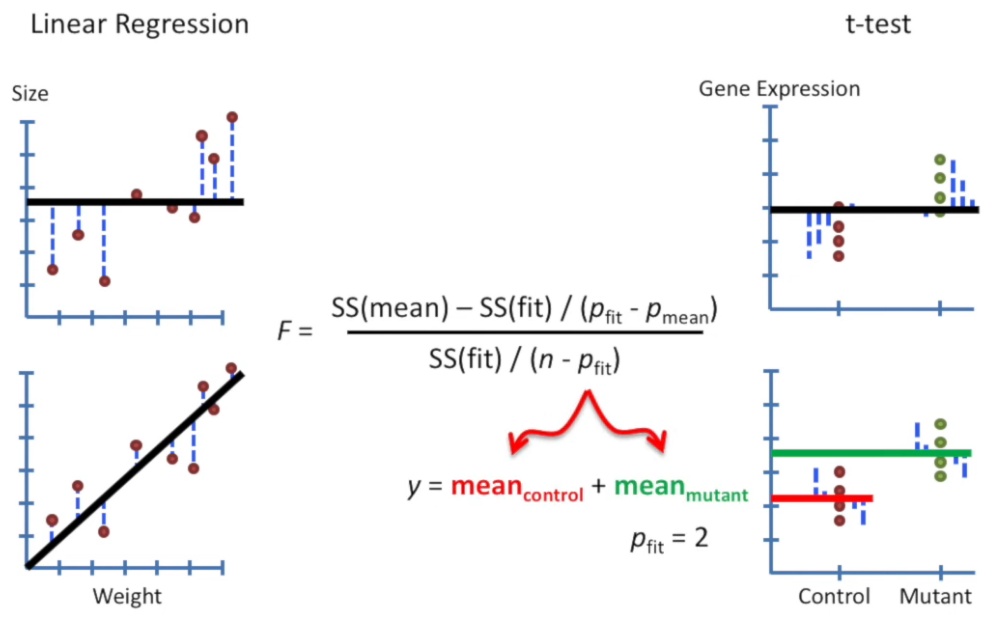
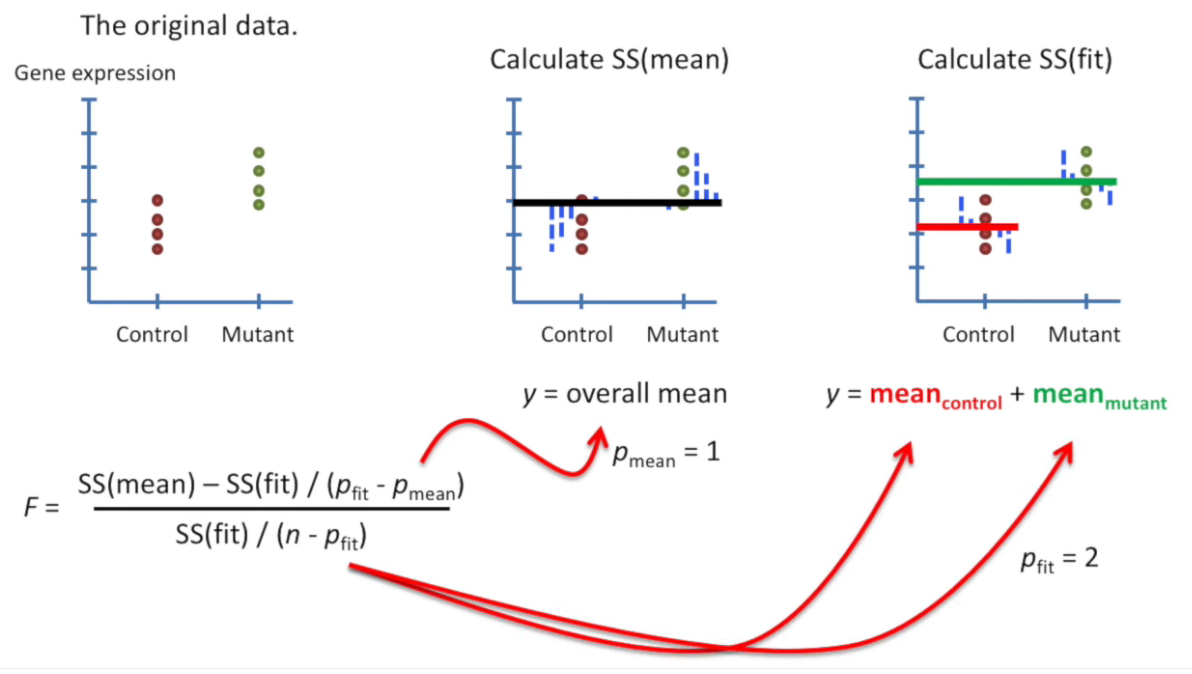
It uses the F-statistic:

If the between-group variance is much larger than the within-group variance, the F-value is large, suggesting the group means are not all equal.

---

✅ Types of ANOVA

1. One-way ANOVA

   • Tests the effect of one categorical independent variable on one continuous dependent variable.

2. Two-way ANOVA

   • Tests the effects of two categorical independent variables and their interaction on a continuous dependent variable.

3. Repeated Measures ANOVA

   • Used when the same subjects are measured multiple times (like before and after treatment).

 

 

 

 

 

 

 

 

 

 

 

     

 

     

 

     

 

     

 

     

 

 

 

 

 

     

 

 

 

 

 

 

 

     

 

 

     

 

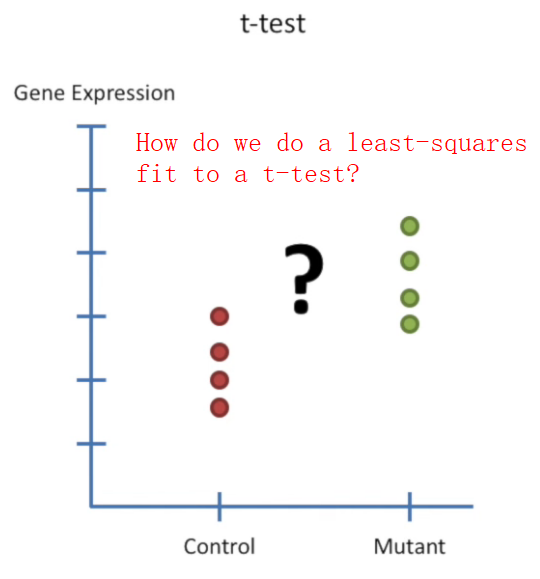
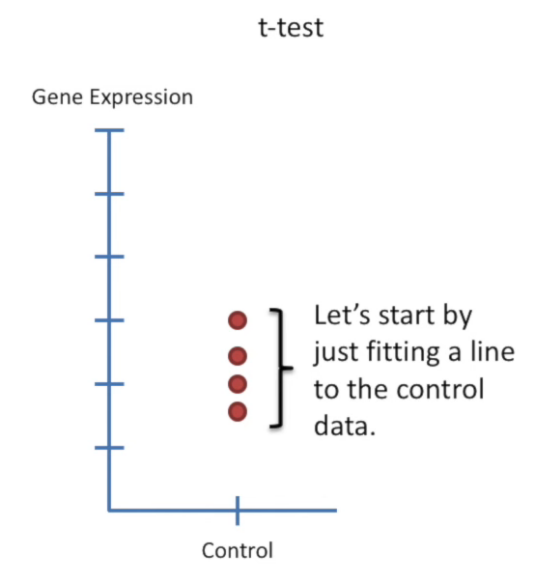
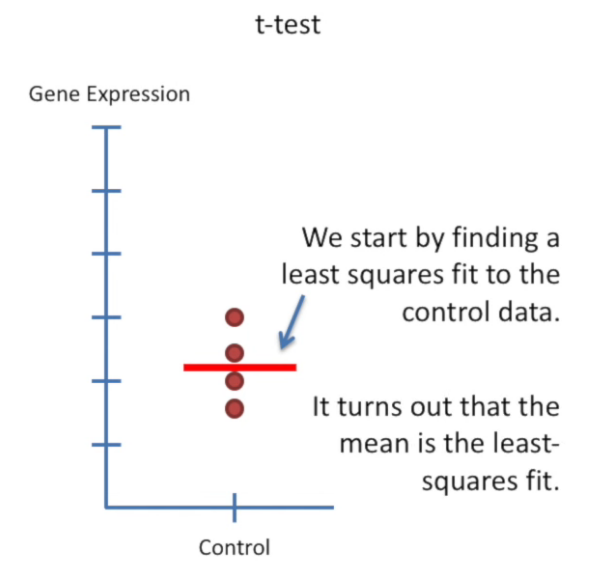
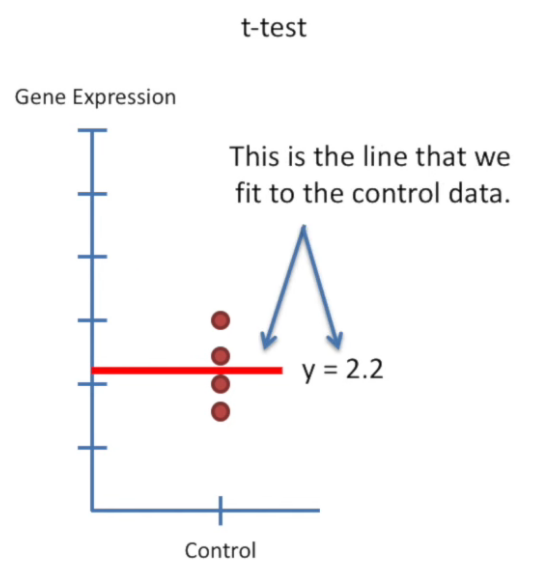
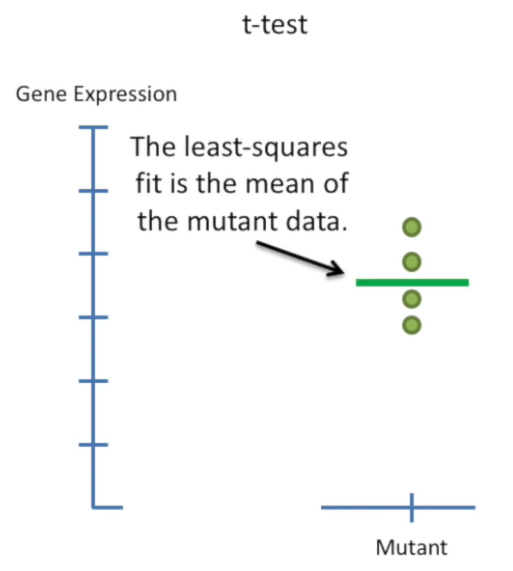
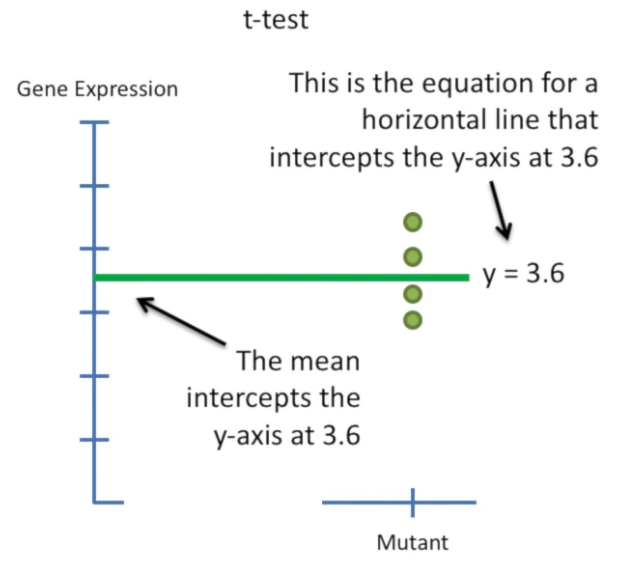
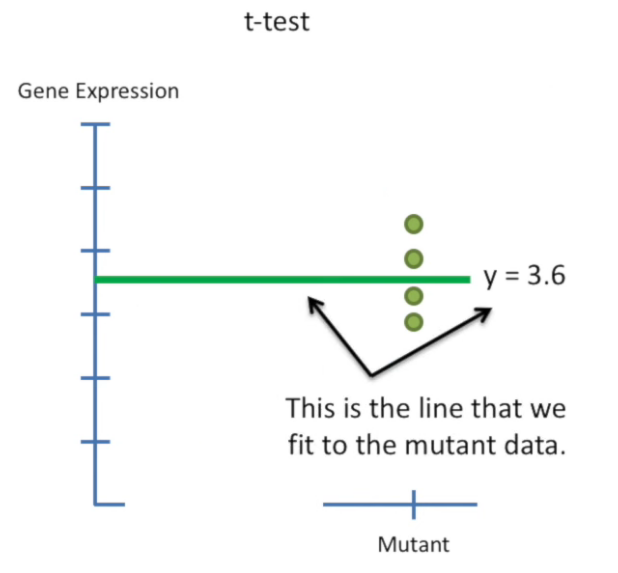
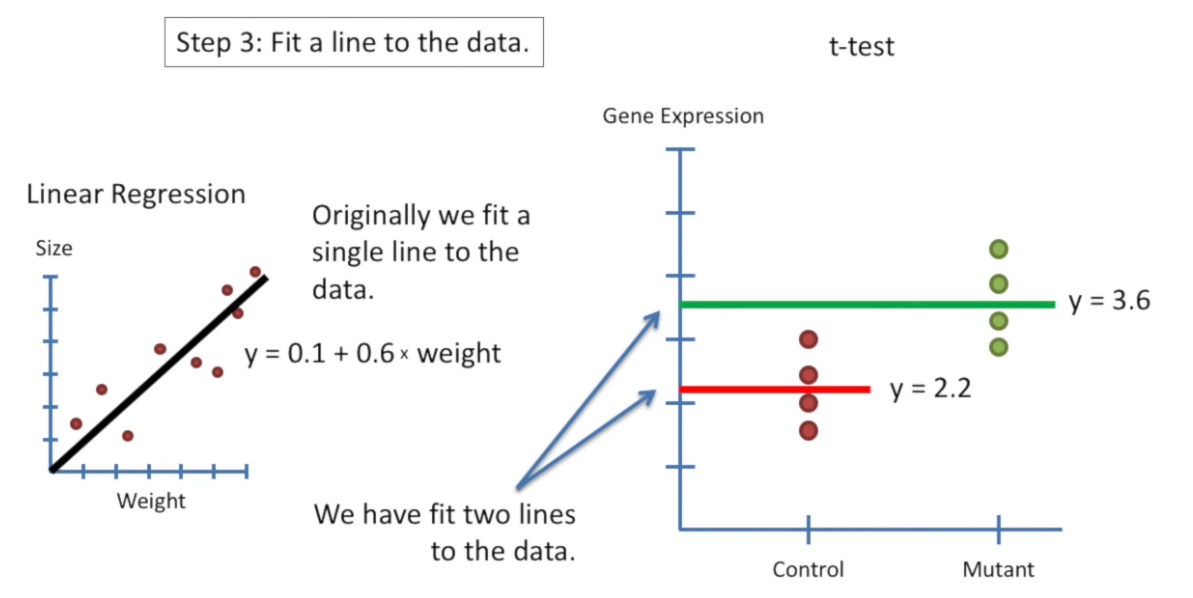
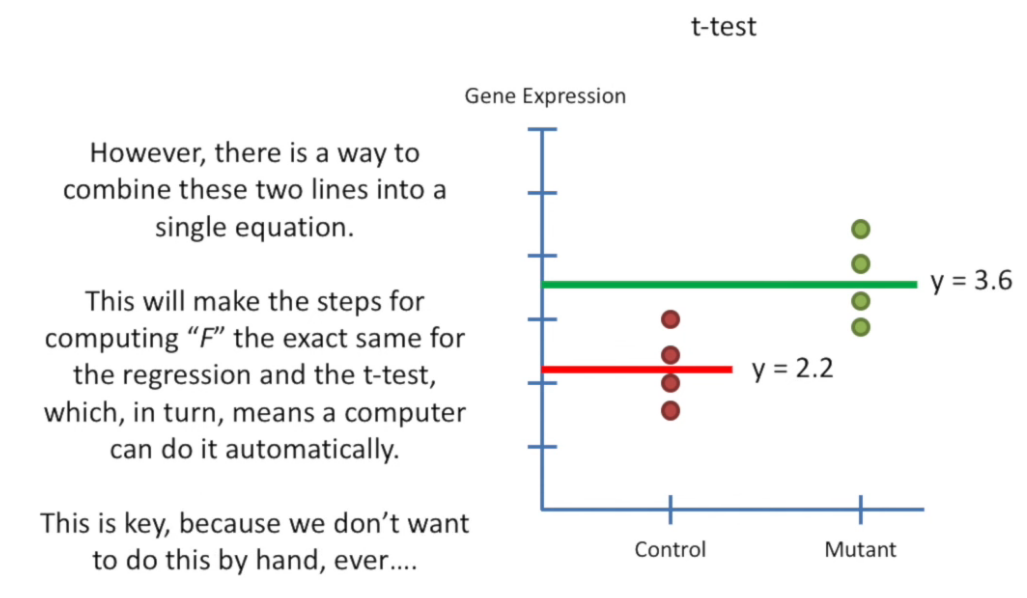
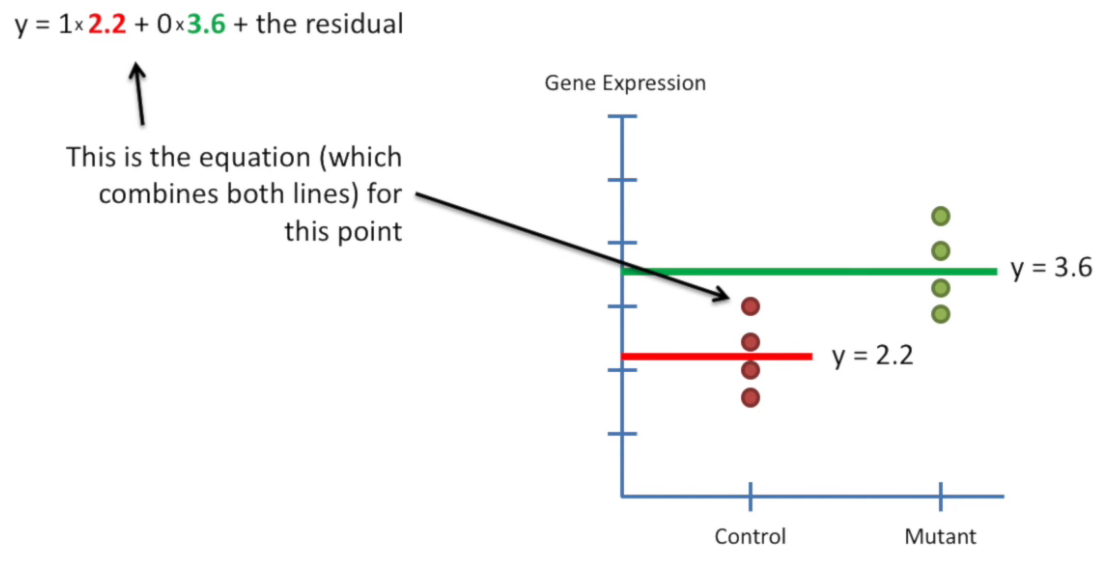
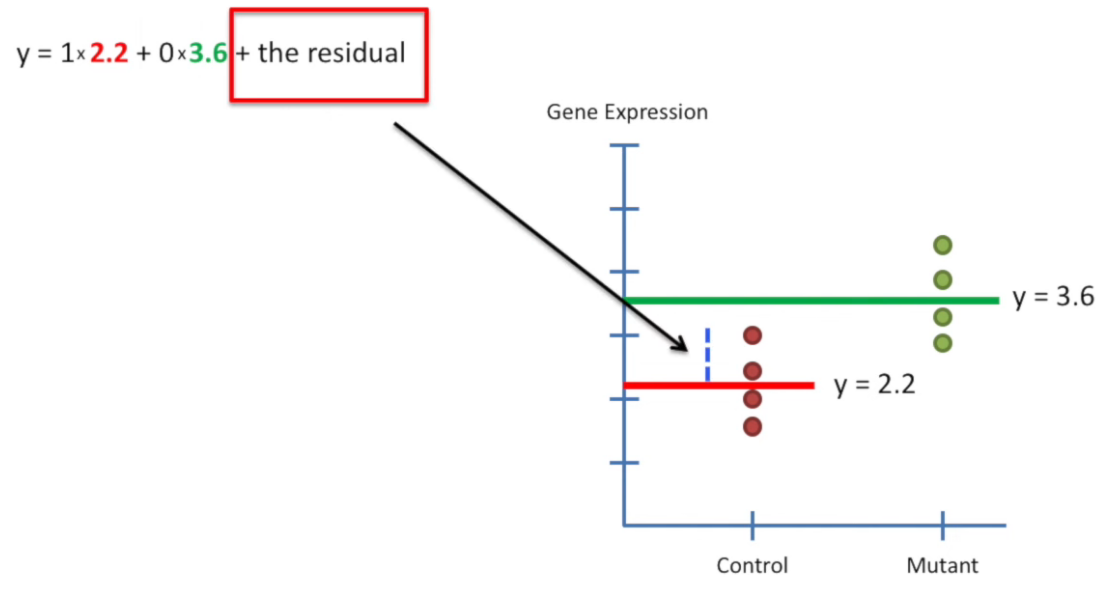
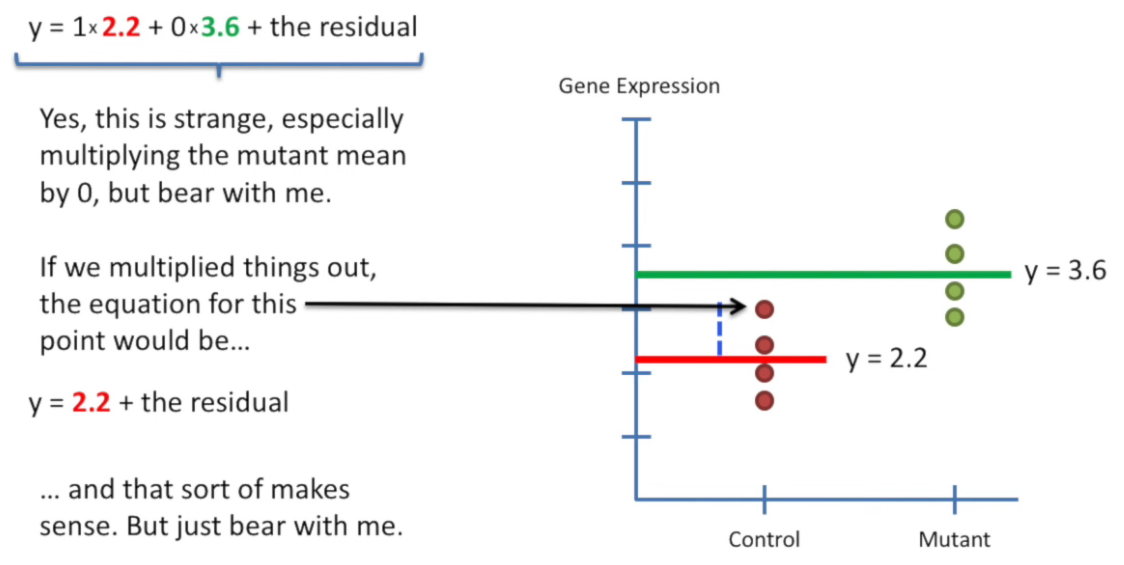
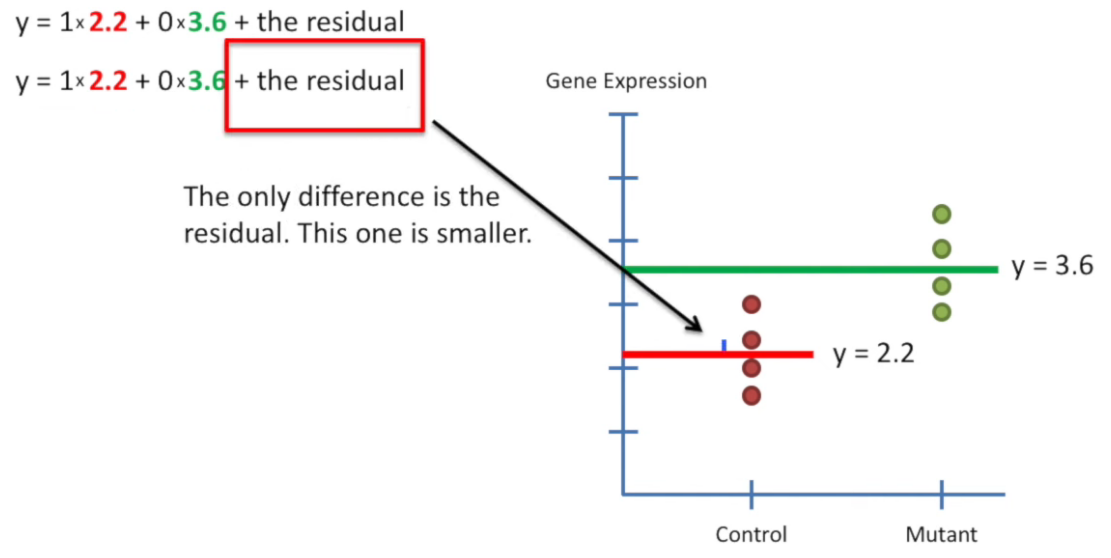
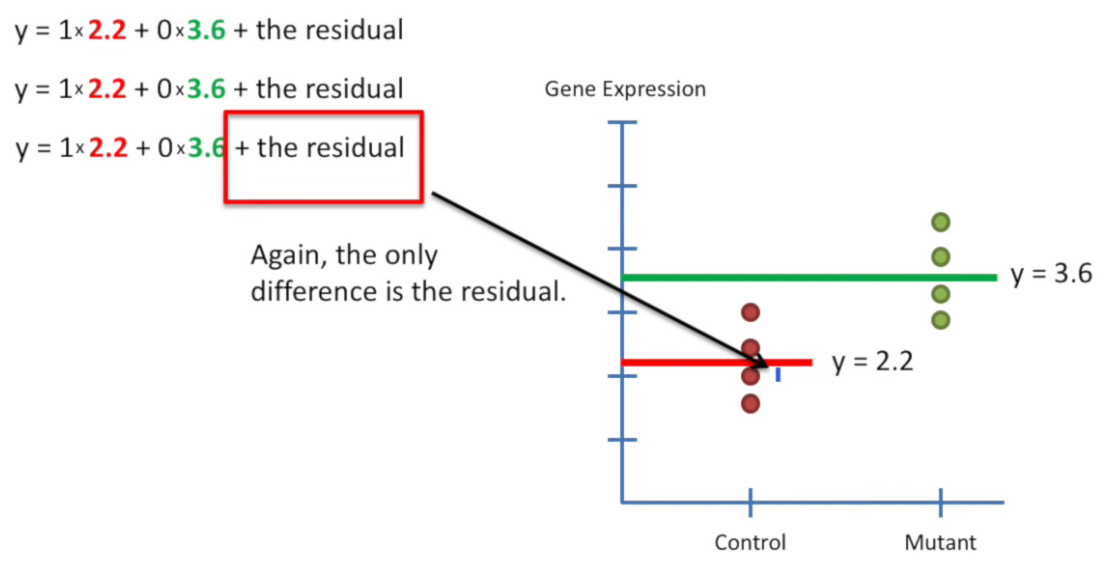
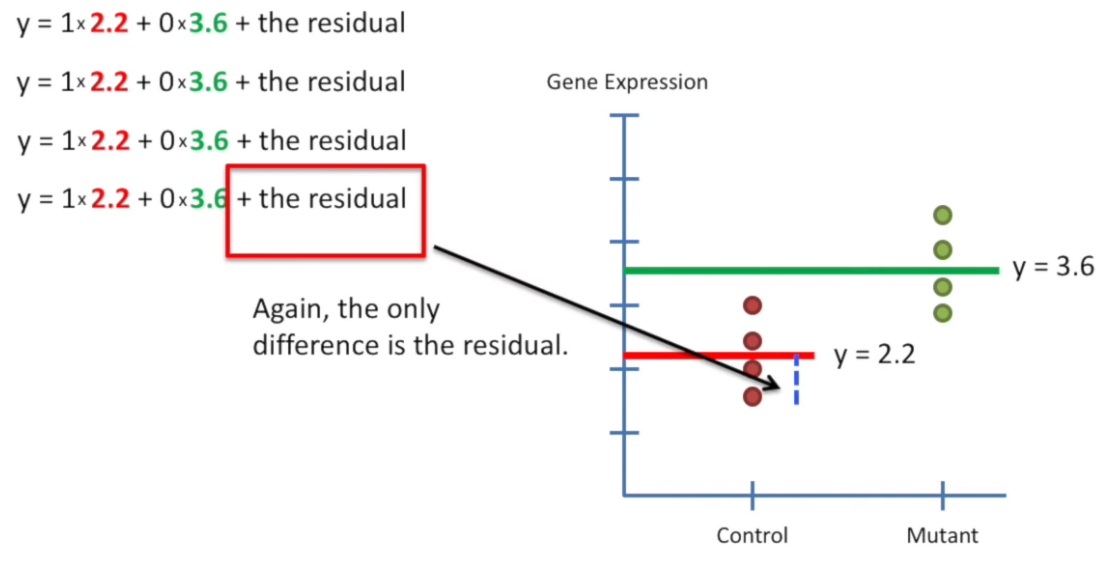
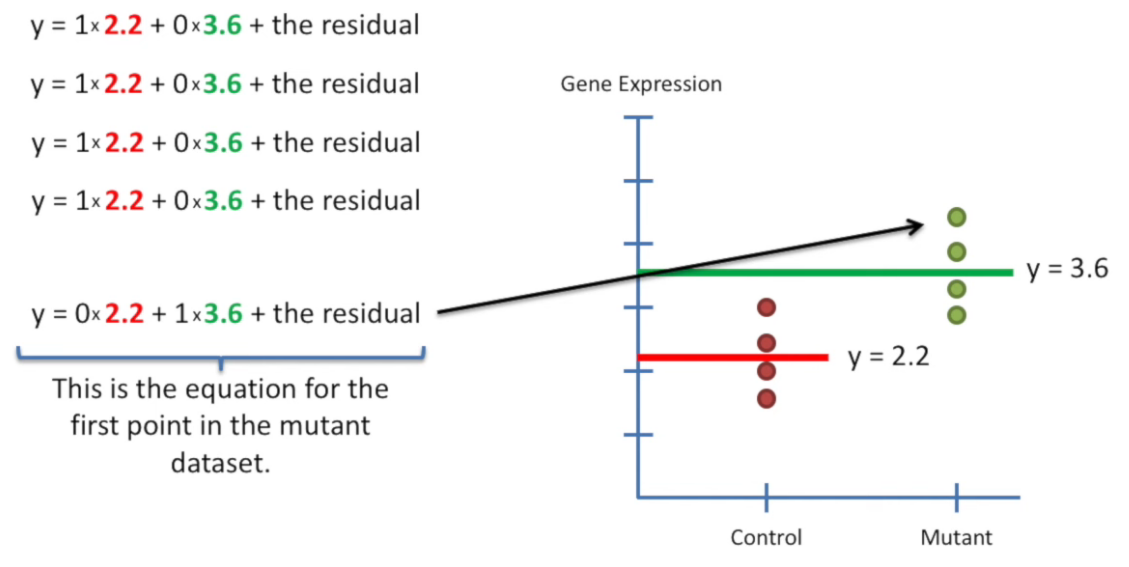
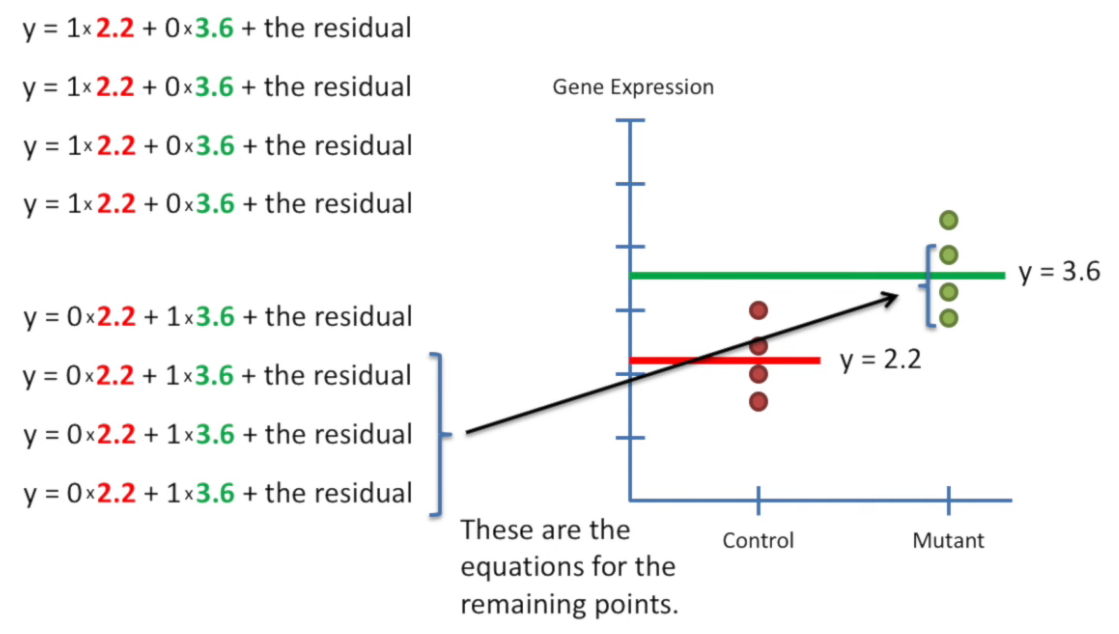
     design matrix