A Concise Introduction to Logic - PART II: FORMAL LOGIC - Chapter 8: Predicate Logic

PART II: FORMAL LOGIC

Chapter 8: Predicate Logic

8.1 Symbols and Translation

Techniques were dev eloped in earlier chapters for evaluating two basically different kinds of arguments. The chapter on categorical syllogisms dealt with arguments such as the following:

In such arguments the fundamental components are terms, and the validity of the argument depends on the arrangement of the terms within the premises and conclusion.

The chapter on propositional logic, on the other hand, dealt with arguments such as this:

In such arguments the fundamental components are not terms but statements. The validity of these arguments depends not on the arrangement of the terms within the statements but on the arrangement of the statements themselves as simple units.

Not all arguments, however, can be assigned to one or the other of these two groups. There is a third type that is a kind of hybrid, sharing features with both categorical syllogisms and propositional arguments. Consider, for example, the following:

The validity of this argument depends on both the arrangement of the terms and the arrangement of the statements. Accordingly, neither syllogistic logic nor propositional logic alone is sufficient to establish its validity. What is needed is a third kind of logic that combines the distinctive features of syllogistic logic and propositional logic. This third kind is called predicate logic.

The fundamental component in predicate logic is the predicate, symbolized by uppercase letters (A, B, C, . . . X, Y, Z), called predicate symbols. Here are some examples of bare predicates:

The blank space immediately following the predicate letter is not part of the predicate; rather, it indicates the place for some lowercase letter that will represent the subject of the statement. Depending on what lowercase letter is used, and on the additional symbolism involved, symbolic predicates may be used to translate three distinct kinds of statements: singular statements, universal statements, and particular statements.

A singular statement, you may recall from Section 4.7, is a statement that makes an assertion about a specifically named person, place, thing, or time. Translating a singular statement involves writing a lowercase letter corresponding to the subject of the statement to the immediate right of the uppercase letter corresponding to the predicate. The letters that are allocated to serve as names of individuals are the first twenty-three letters of the alphabet (a, b, c, . . . u, v, w). These letters are called individual constants. Here are some examples of translated statements:

Compound arrangements of singular statements may be translated by using the familiar connectives of propositional logic. Here are some examples:

Recall from Chapter 4 that a universal statement is a statement that makes an assertion about every member of its subject class. Such statements are either affirmative or negative, depending on whether the statement affirms or denies that the members of the subject class are members of the predicate class. The key to translating universal statements is provided by the Boolean interpretation of these statements (see Section 4.3):

According to the Boolean interpretation, universal statements are translated as conditionals. We have a symbol (the horseshoe) to translate conditional statements, so we may use it to translate universal statements. What is still needed, however, is a symbol to indicate that universal statements make an assertion about every member of the S class. This symbol is called the universal quantifier. It is formed by placing a lowercase letter in parentheses, (x), and is translated as “for any x.” The letters that are allocated for forming the universal quantifier are the last three letters of the alphabet (x, y, z). These letters are called individual variables.

The horseshoe operator and the universal quantifier are combined to translate universal statements as follows:

An individual variable differs from an individual constant in that it can stand for any item at random in the universe. Accordingly, the expression (x)(Sx ⊃ Px) means “If anything is an S, then it is a P,” and (x)(Sx ⊃ ∼Px) means “If anything is an S, then it is not a P.” The fact that these expressions are equivalent to the Boolean interpretation of universal statements may be seen by recalling how the Boolean interpretation is represented by Venn diagrams (see Section 4.3). The Venn diagrams corresponding to the two universal statement forms are as follows:

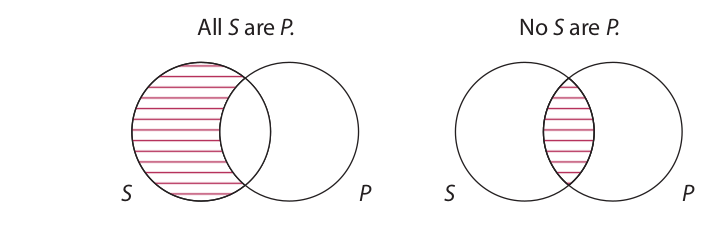
Where shading designates emptiness, the diagram on the left asserts that if anything is in the S circle, it is also in the P circle, and the one on the right asserts that if anything is in the S circle, it is not in the P circle. This is exactly what is asserted by the symbolic expressions just given. These symbolic expressions may therefore be taken as being exactly synonymous with the Boolean interpretation of universal statements.

A possible source of confusion at this point concerns the fact that both S and P in the symbolic expressions are predicates, whereas in the original statement forms S is the subject and P is the predicate. Any problem in this regard vanishes, however, once one understands what happens when universal statements are converted into conditionals. When so converted, S becomes the predicate of the antecedent and P becomes the predicate of the consequent. In other words, in the conditional “If anything is an S, then it is a P,” both S and P are predicates. Thus, using predicate symbolism to translate universal statements leads to no difficulties. When translating these statements, the point to remember is simply this: The subject of the original statement is represented by a capital letter in the antecedent, and the predicate by a capital letter in the consequent. Here are some examples:

In these examples, the expressions Sx ⊃ Tx, Fx ⊃ ∼Bx, and so on are called statement functions. A statement function is the expression that remains when a quantifier is removed from a statement. It is a mere pattern for a statement. It makes no definite assertion about anything in the universe, has no truth value, and cannot be translated as a statement. The variables that occur in statement functions are called free variables because they are not bound by any quantifier. In contrast, the variables that occur in statements are called bound variables.

In using quantifiers to translate statements, we adopt a convention similar to the one adopted for the tilde operator. That is, the quantifier governs only the expression immediately following it. For example, in the statement (x)(Ax ⊃ Bx) the universal quantifier governs the entire statement function in parentheses—namely, Ax ⊃ Bx. But in the expression (x)Ax ⊃ Bx, the universal quantifier governs only the statement function Ax. The same convention is adopted for the existential quantifier, which will be introduced presently.

Recall from Chapter 4 that a particular statement is a statement that makes an assertion about one or more unnamed members of the subject class. As with universal statements, particular statements are either affirmative or negative, depending on whether the statement affirms or denies that members of the subject class are members of the predicate class. Also, as with universal statements, the key to translating particular statements is provided by the Boolean interpretation:

In other words, particular statements are translated as conjunctions. Since we are already familiar with the symbol for conjunction (the dot), the only additional symbol that we need in order to translate these statements is a symbol for existence. This is provided by the existential quantifier, formed by placing a variable to the right of a backward E in parentheses, thus: (∃x). This symbol is translated “there exists an x such that.” The existential quantifier is combined with the dot operator to translate particular statements as follows:

As in the symbolic expression of universal statements, the letter x is an individual variable, which can stand for any item in the universe. Accordingly, the expression (∃x)(Sx • Px) means “Something exists that is both an S and a P,” and (∃x)(Sx • ∼Px) means “Something exists that is an S and not a P.” To see the equivalence of these expressions with the Boolean (and Aristotelian) interpretation of particular statements, it is again useful to recall how these statements are represented by Venn diagrams:

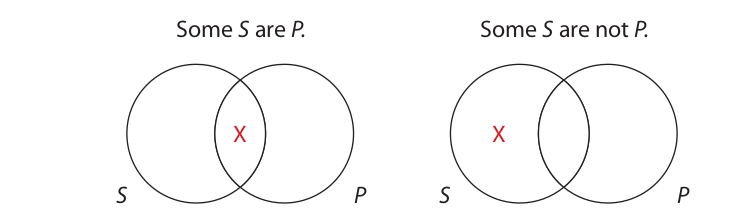
Where the X designates at least one existing item, the diagram on the left asserts that something exists that is both an S and a P, and the one on the right asserts that something exists that is an S and not a P. In other words, these diagrams assert exactly the same thing as the symbolic expressions just given. These symbolic expressions, therefore, exactly express the Boolean (and Aristotelian) interpretation of particular statements. Here are some examples:

The general rule to follow in translating statements in predicate logic is always to make an effort to understand the meaning of the statement to be translated. If the statement makes an assertion about every member of its subject class, a universal quantifier should be used to translate it; but if it makes an assertion about only one or more members of this class, an existential quantifier should be used.

Many of the principles developed in syllogistic logic (see Section 4.7) may be carried over into predicate logic. Specifically, it should be understood that statements beginning with the words only and none but are exclusive propositions. When these statements are translated, the term occurring first in the original statement becomes the consequent in the symbolic expression, and the term occurring second becomes the antecedent. One of the few differences in this respect between predicate logic and syllogistic logic concerns singular statements. In syllogistic logic, singular statements are translated as universals, while in predicate logic, as we have seen, they are translated in a unique way. Here are some examples of a variety of statements:

As these examples illustrate, the general procedure in translating statements in predicate logic is to render universal statements as conditionals preceded by a universal quantifier, and particular statements as conjunctions preceded by an existential quantifier. However, as the third and fifth examples indicate, there are exceptions to this procedure. A statement that makes an assertion about literally everything in the universe is translated in terms of a single predicate preceded by a universal quantifier, and a statement that asserts that some class of things simply exists is translated in terms of a single predicate preceded by an existential quantifier. The last two examples illustrate that a particular statement is equivalent to a negated universal, and vice versa. The first of these is equivalent to “Some Girl Scouts do not sell cookies” and the second to “No psychologists attended the convention.” Actually, any quantified statement can be translated using either a universal or an existential quantifier, provided that one of them is negated. The equivalence of these two forms of expression will be analyzed further in Section 8.3.

More complex statements may be translated by following the basic rules just presented. Examples:

Notice that the first example is translated in terms of the disjunction Sx ∨ Lx even though the English statement reads “snakes and lizards.” If the translation were rendered as (x)[Tx ⊃ (Sx • Lx)] it would mean that anything that thrives in the desert is both a snake and a lizard (at the same time). And this is surely not what is meant. For the same reason, the second example is translated in terms of the disjunction Ox ∨ Lx even though the English reads “oranges and lemons.” If the statement were translated (x)[(Ox • Lx) ⊃ Cx], it would mean that anything that is simultaneously an orange and a lemon (and there are none of these) is a citrus fruit. The same principle is used in translating the sixth example, which, incidentally, reads “If anything is a cat or a dog, then if it is frightened or harassed, it bites.” The third example employs the conjunction Rx • Ax to translate ripe apples. This, of course, is correct, because such a thing is both ripe and an apple at the same time. The fifth example illustrates the fact that “unless” may be translated as either “if not” or “or.”

The operators of propositional logic can be used to form compound arrangements of universal and particular statements, just as they can be used to form compound arrangements of singular statements. Here are some examples:

We have seen that the general procedure is to translate universal statements as conditionals preceded by a universal quantifier, and to translate particular statements as conjunctions preceded by an existential quantifier. Let us see what happens to these translations when they are preceded by the wrong quantifier. Consider the false statement “No cats are animals.” This is correctly translated (x)(Cx ⊃ ∼Ax). If, however, it were translated (∃x)(Cx ⊃ ∼Ax), the symbolic statement would turn out to be true. This may be seen as follows. (∃x)(Cx ⊃ ∼Ax) is equivalent via material implication to (∃x)(∼Cx ∨ ∼Ax), which in turn is equivalent via De Morgan’s rule to (∃x)∼(Cx • Ax). The latter statement, however, merely asserts that something exists that is not both a cat and an animal—for example, a dog—which is true. Again, consider the true statement “Some cats are animals.” This is correctly translated (∃x)(Cx • Ax). If, however, it were translated (x)(Cx • Ax), the symbolic statement would assert that everything in the universe is both a cat and an animal, which is clearly false. Thus, as these examples illustrate, it is imperative that the two quantifiers not be confused with each other.

One final observation needs to be made. It was mentioned earlier that the letters x, y, and z are reserved for use as variables for translating universal and particular statements. In accord with this convention, the other twenty-three lowercase letters (a, b, c, . . . u, v, w) may be used as names for translating singular statements. Thus, for example, “Albert is a scientist” is translated Sa. But a question naturally arises with statements such as “Xerxes was a king.” Should this statement be translated Kx? The answer is no. Some other letter, for example the second letter in the name, should be selected instead of x. Maintaining this alphabetical convention will help us avoid mistakes in the next section when we use natural deduction to derive the conclusions of arguments.

 

8.2 Using the Rules of Inference

The chief reason for using truth-functional operators (the dot, wedge, horseshoe, and so on) in translating statements into the symbolism of predicate logic is to allow for the application of the eighteen rules of inference to derive the conclusion of arguments via natural deduction. Since, however, the first eight of these rules are applicable only to whole lines in an argument, as long as the quantifier is attached to a line these rules of inference cannot be applied—at least not to the kind of arguments we are about to consider. To provide for their application, four additional rules are required to remove quantifiers at the beginning of a proof sequence and to introduce them, when needed, at the end of the sequence. These four rules are called universal instantiation, universal generalization, existential instantiation, and existential generalization. The first two are used to remove and introduce universal quantifiers, respectively, and the second two to remove and introduce existential quantifiers.

Let us first consider universal instantiation. As an illustration of the need for this rule, consider the following argument:

This argument, which is clearly valid, is symbolized as follows:

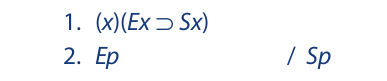
As the argument now stands, none of the first eight rules of inference can be applied; as a result, there is no way in which the two premises can be combined to derive the conclusion. However, if the first premise could be used to derive a line that reads Ep ⊃ Sp, this statement could be combined with the second premise to yield the conclusion via modus ponens. Universal instantiation serves exactly this purpose.

The first premise states that for any item x in the universe, if that item is an E, then it is an S. But since Paul Krugman is himself an item in the universe, the first premise implies that if Paul Krugman is an E, then Paul Krugman is an S. A line stating exactly this can be derived by universal instantiation (UI). In other words, universal instantiation provides us with an instance of the universal statement (x)(Ex ⊃ Sx). In the completed proof, which follows, the p in line 3 is called the instantial letter:

At this point the question might arise as to why modus ponens is applicable to lines 2 and 3. In Chapter 7 we applied modus ponens to lines of the form p ⊃ q, but are we justified in applying it to a line that reads Ep ⊃ Sp? The answer is yes, because Ep and Sp are simply alternate ways of symbolizing simple statements. As so understood, these symbols do not differ in any material way from the p and q of propositional logic.

We may now give a general definition of instantiation. Instantiation is an operation that consists in deleting a quantifier and replacing every variable bound by that quantifier with the same instantial letter. For an example of an operation that violates the rule expressed in this definition, consider line 3 of the foregoing proof. If this line were instantiated as Ep ⊃ Sx, it would not be correct because the x in Sx was not replaced with the instantial letter p.

Let us now consider universal generalization. The need for this rule may be illustrated through reference to the following argument:

This valid argument is symbolized as follows:

Once universal instantiation is applied to the two premises, we will have lines that can be used to set up a hypothetical syllogism. But then we will have to reintroduce a universal quantifier to derive the conclusion as written. This final step is obtained by universal generalization (UG). The justification for such a step lies in the fact that both premises are universal statements. The first states that if anything is a P, then it is a D, and the second states that if anything is a D, then it is a C. We may therefore conclude that if anything is a P, then it is a C. But because of the complete generality of this reasoning process, there is a special way in which we must perform the universal instantiation step. Instead of selecting a specifically named instance, as we did in the previous example, we must select a variable that can range over every instance in the universe. The variables at our disposal, you may recall from the previous section, are x, y, and z. Let us select y. The completed proof is as follows:

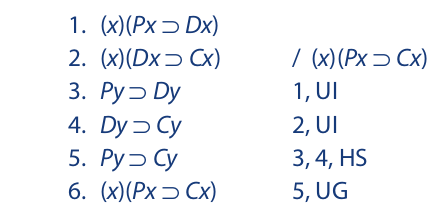
As noted earlier, the expressions in lines 3, 4, and 5 are called statement functions. As such, they are mere patterns for statements; they have no truth value and cannot be translated as statements. Yet if we take certain liberties, we might characterize line 5 as saying “If it is a P, then it is a C, where “it” designates any item at random in the universe. Line 6 can then be seen as reexpressing this sense of line 5.

As the two previous examples illustrate, we have two ways of performing universal instantiation. On the one hand, we may instantiate with respect to a constant, such as a or b, and on the other, with respect to a variable, such as x or y. The exact way in which this operation is to be performed depends on the kind of result intended. If we want some part of a universal statement to match a singular statement on another line, as in the first example, we instantiate with respect to a constant. But if, at the end of the proof, we want to perform universal generalization over some part of the statement we are instantiating, then we must instantiate by using a variable. This latter point leads to an important restriction governing universal generalization—namely, that we cannot perform this operation when the instantial letter is a constant. Consider the following erroneous proof sequence:

If Ta means “Albert is a thief,” then on the basis of this information, we have concluded (line 2) that everything in the universe is a thief. Clearly, such an inference is invalid. This illustrates the fact that universal generalization can be performed only when the instantial letter (in this case a) is a variable.

Let us now consider existential generalization. The need for this operation is illustrated through the following argument:

This argument is symbolized as follows:

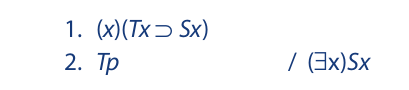
If we instantiate the first line with respect to p, we can obtain Sp via modus ponens. But if it is true that Placido Domingo is a tenor, then it certainly follows that there is at least one singer (namely, Placido Domingo). This last step is accomplished by existential generalization (EG). The proof is as follows:

There are no restrictions on existential generalization, and the operation can be performed when the instantial letter is either a constant (as in the Domingo example) or a variable. As an instance of the latter, consider the following sequence:

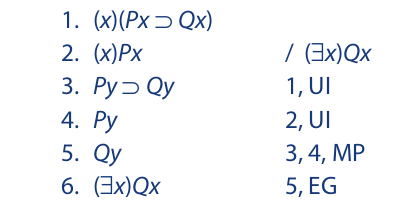
Line 5 states in effect that everything in the universe is a Q. From this, the much weaker conclusion follows (line 6) that something is a Q. If you should wonder how an existential conclusion can be drawn from universal premises, the answer is that predicate logic assumes that at least one thing exists in the universe. Hence, line 2, which asserts that everything in the universe is a P, entails that at least one thing is a P. Without this assumption, universal instantiation in line 4 would not be possible.

We may now construct a definition of generalization that covers both varieties. Generalization in the inclusive sense is an operation that consists in (1) introducing a quantifier immediately prior to a statement, a statement function, or another quantifier, and (2) replacing one or more occurrences of a certain instantial letter in the statement or statement function with the same variable that appears in the quantifier. For universal generalization, all occurrences of the instantial letter must be replaced with the variable in the quantifier, and for existential generalization, at least one of the instantial letters must be replaced with the variable in the quantifier. Thus, both of the following cases of existential generalization are valid (although the one on the left is by far the more common version):

On the other hand, only one of the following cases of universal generalization is valid:

The inference on the right is invalid because the x in Gx was not replaced with the variable in the quantifier (that is, y).

Of course, it may happen that the instantial letter is the same as the variable that appears in the quantifier. Thus, the operation “Gx, therefore (x)Gx” counts as a generalization. Cases of generalization where a quantifier is introduced prior to another quantifier will be presented in Section 8.6.

The need for existential instantiation can be illustrated through the following argument:

The symbolic formulation is as follows:

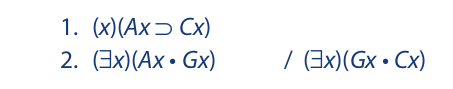
If both quantifiers can be removed, the conclusion can be derived via simplification, modus ponens, and conjunction. The universal quantifier can be removed by universal instantiation, but to remove the existential quantifier we need existential instantiation. Line 2 states that there is something that is both an A and a G. Existential instantiation consists in giving this something a name, for example, “David.” We will call this name an “existential name” because it is obtained through existential instantiation. The completed proof is as follows:

Examination of this proof reveals an immediate restriction that must be placed on existential instantiation. The name that we have assigned to the particular something in line 2 that is both an A and a G is a hypothetical name. It would be a mistake to conclude that this something really has that name. Accordingly, we must introduce a restriction that prevents us from ending the proof with some line that includes the letter d. If, for example, the proof were ended at line 9, we would be concluding that the something that is a G and a C really does have the name d. This, of course, would not be legitimate, because d is an arbitrary name introduced into the proof for mere convenience. To prevent such a mistake, we require that the name selected for existential instantiation not appear to the right of the slanted line adjacent to the last premise that indicates the conclusion to be derived. Since the last line in the proof must be identical to this line, such a restriction prevents us from ending the proof with a line that contains the existential name.

Further examination of this proof indicates another important restriction on existential instantiation. Notice that the line involving existential instantiation is listed before the line involving universal instantiation. There is a reason for this. If the order were reversed, the existential instantiation step would rest on the illicit assumption that the something that is both an A and a G has the same name as the name used in the earlier universal instantiation step. In other words, it would involve the assumption that the something that is both an A and a G is the very same something named in the line Ad ⊃ Cd. Of course, no such assumption is legitimate. To keep this mistake from happening, we introduce the restriction that the name introduced by existential instantiation be a new name not occurring earlier in the proof sequence. The following defective proof illustrates what can happen if this restriction is violated:

To see that this proof is indeed defective, let F stand for fruits, A for apples, and O for oranges. The argument that results is:

Since the premises are true and the conclusion false, the argument is clearly invalid. The defect in the proof occurs on line 4. This line asserts that the something that is both an F and an O is the very same something that is both an F and an A. In other words, the restriction that the name introduced by existential instantiation be a new name not occurring earlier in the proof is violated.

The first restriction on existential instantiation requires that the existential name not occur in the line that indicates the conclusion to be derived, and the second restriction requires that this name be a new name that has not occurred earlier in the proof. These two restrictions can easily be combined into a single restriction that requires that the name introduced by existential instantiation be a new name that has not occurred in any previous line, including the line adjacent to the last premise that indicates the conclusion to be derived.

One further restriction that affects all four of these rules of inference requires that the rules be applied only to whole lines in a proof. The following sequence illustrates a violation of this restriction:

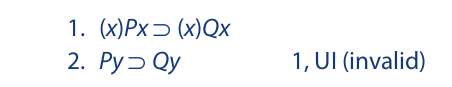
In line 2 universal instantiation is applied to both the antecedent and consequent of the first line. To derive line 2 validly, the first line would have to read (x)(Px ⊃ Qx). With this final restriction in mind, the four new rules of inference may now be summarized. In the formulation that follows, the symbols ␂x and ␂y represent any statement function—that is, any symbolic arrangement containing individual variables, such as Ax ⊃ Bx, Cy ⊃ (Dy ∨ Ey), or Gz • Hz. And the symbol ␂a represents any statement; that is, any symbolic arrangement containing individual constants (or names), such as Ac ⊃ Bc, Cm ⊃ (Dm ∨ Em), or Gw • Hw:

The not allowed version of universal generalization recalls the already familiar fact that generalization is not possible when the instantial letter is a constant. In other words, the mere fact that the individual a is an ␂ is not sufficient to allow us to conclude that everything in the universe is an ␂. At present this is the only restriction needed for universal generalization. In Sections 8.4 and 8.6, however, two additional restrictions will be introduced. The not allowed version of existential instantiation merely recalls the fact that this operation is a naming process. Because variables (x, y, and z) are not names, they cannot be used as instantial letters in existential instantiation.

Let us now investigate some applications of these rules. Consider the following proof:

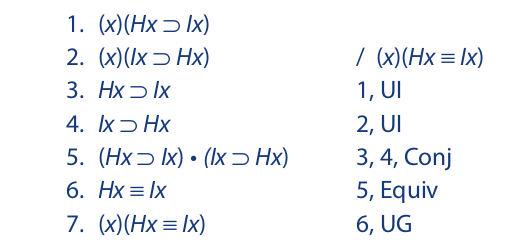
Because we want to perform universal generalization on the last line of the proof, we instantiate lines 1 and 2 using a variable, not a constant. Notice that the variable selected for lines 3 and 4 is the same letter that occurs in lines 1 and 2. While a new letter (y or z) could have been selected, this is never necessary in such a step. It is necessary, however, since we want to combine lines 3 and 4, that the same variable be selected in deriving these lines. Another example:

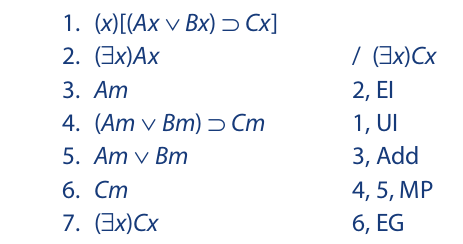
In conformity with the restriction on existential instantiation, the EI step is performed before the UI step. The same letter is then selected in the UI step as was used in the EI step. In line 5, Bm is joined disjunctively via addition to Am. This rule applies in predicate logic in basically the same way that it does in propositional logic. Any statement or statement function we choose can be joined disjunctively to a given line.

Another example:

Since the instantiation (and generalization) rules must be applied to whole lines, it is impossible to instantiate line 1. The only strategy that can be followed is to use some other line to derive the antecedent of this line and then derive the consequent via modus ponens. Once the consequent is derived (line 5), it is instantiated using the same letter that appears in line 2.

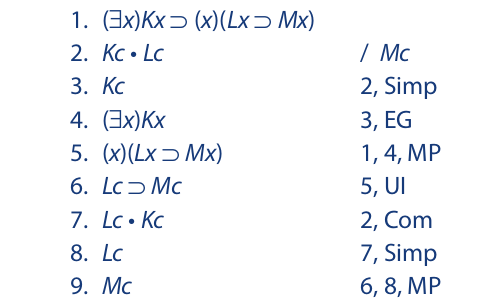
The next example incorporates all four of the instantiation and generalization rules:

As with the previous example, line 1 cannot be instantiated. To instantiate the two conjuncts in line 2, they must first be separated (lines 3 and 5). Because UG is to be used in line 9, lines 3 and 5 are instantiated using a variable. On the other hand, a constant is used to instantiate line 10 because the statement in question is a particular statement.

Another example:

When line 2 is instantiated (line 4), a letter other than j, which appears in line 1, is selected. Then, when line 3 is instantiated (line 5), another new letter is selected. The conclusion is derived, as in earlier examples, via modus ponens by deriving the antecedent of line 1.

The following examples illustrate invalid or improper applications of the instantiation and generalization rules:

 

8.3 Change of Quantifier Rule

The rules of inference developed thus far are not sufficient to derive the conclusion of every argument in predicate logic. For instance, consider the following:

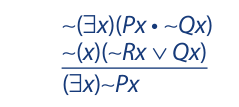
Both premises have tildes preceding the quantifiers. As long as they remain, neither statement can be instantiated; and if these statements cannot be instantiated, the conclusion cannot be derived. What is needed is a rule that will allow us to remove the negation signs. This rule, which we will proceed to develop now, is called the change of quantifier rule.

As a basis for developing the change of quantifier rule, consider the following statements:

You should be able to see that these statements are equivalent in meaning to the following statements, respectively:

If we generalize these English equivalencies symbolically, we obtain:

These four expressions constitute the change of quantifier rule (CQ). Since they are stated as logical equivalences, they apply to parts of lines as well as to whole lines. They can be summarized as follows:

To see how the change of quantifier rule is applied, let us return to the argument at the beginning of this section. The proof is as follows:

Before either line 1 or line 2 can be instantiated, the tilde operators preceding the quantifiers must be removed. In accordance with the change of quantifier rule, tilde operators are introduced immediately after the new quantifiers in the expressions on lines 3 and 4.

Another example:

The statement that m is not an I (line 2) intuitively implies that not everything is an I (line 4); but existential generalization and change of quantifier are needed to get the desired result. Notice that lines 7 and 8 are derived via De Morgan’s rule and material implication, even though the quantifier is still attached. Since these rules are rules of replacement, they apply to parts of lines as well as to whole lines. The following example illustrates the same point with respect to the change of quantifier rule:

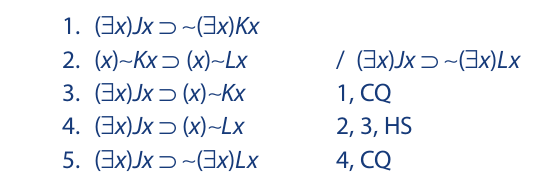
The change of quantifier rule is applied to only the consequent of line 1, yielding line 3. Similarly, the change of quantifier rule is then applied to only the consequent of line 4, yielding line 5.

 

8.4 Conditional and Indirect Proof

Many arguments with conclusions that are either difficult or impossible to derive by the conventional method can be handled with ease by using either conditional or indirect proof. The use of these techniques on arguments in predicate logic is basically the same as it is on arguments in propositional logic. Arguments having conclusions expressed in the form of conditional statements or disjunctions (which can be derived from conditional statements) are immediate candidates for conditional proof. For these arguments, the usual strategy is to put the antecedent of the conditional statement to be obtained in the first line of an indented sequence, to derive the consequent as the last line, and to discharge the conditional sequence in a conditional statement that exactly matches the one to be obtained. Here is an example of such a proof:

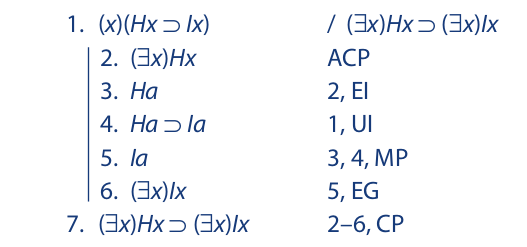
In this argument the antecedent of the conclusion is a complete statement consisting of a statement function, Hx, preceded by a quantifier. This complete statement is assumed as the first line in the conditional sequence. The instantiation and generalization rules are used within an indented sequence (both conditional and indirect) in basically the same way as they are in a conventional sequence. When the consequent of the conclusion is derived, the conditional sequence is completed, and it is then discharged in a conditional statement having the first line of the sequence as its antecedent and the last line as its consequent.

The next example differs from the previous one in that the antecedent of the conclusion is a statement function, not a complete statement. With arguments such as this, only the statement function is assumed as the first line in the conditional sequence. The quantifier is added after the sequence is discharged.

This example leads to an important restriction on the use of universal generalization. You may recall that the x in line 2 of this proof is said to be free because it is not bound by any quantifier. (In contrast, the x’s in lines 1 and 7 are bound by quantifiers.) The restriction is as follows:

The proof just given does not violate this restriction, because UG is not used within the scope of the indented sequence at all. It is used only after the sequence has been discharged, which is perfectly acceptable. If, on the other hand, UG had been applied to line 5 to produce a statement reading (x)Cx, the restriction would have been violated because the instantial variable x is free in the first line of the sequence.

To understand why this restriction is necessary, consider the following defective proof:

If Rx means “x is a rabbit” and Sx means “x is a snake,” then the premise translates “If everything in the universe is a rabbit, then everything in the universe is a snake.” This statement is true because the antecedent is false; that is, it is not the case that everything in the universe is a rabbit. The conclusion, on the other hand, is false, because it asserts that all rabbits are snakes. The argument is therefore invalid. If the restriction on UG had been obeyed, UG could not have been used on line 3 and, as a result, the illicit conclusion could not have been derived.

It is interesting to see what happens when the premise and the conclusion of this defective argument are switched. The proof, which is perfectly legitimate, is as follows:

Notice in this proof that UG is used within the scope of a conditional sequence, but the restriction is not violated because the instantial variable x is not free in the first line of the sequence.

Let us now consider some examples of indirect proof. We begin an indirect sequence by assuming the negation of the statement to be obtained. When a contradiction is derived, the indirect sequence is discharged by asserting the denial of the original assumption. In the examples that follow, the negation of the conclusion is assumed as the first line of the sequence, and the change of quantifier rule is then used to eliminate the tilde. When the resulting statement is then instantiated, a new letter, m, is selected that has not appeared anywhere in a previous line. The same letter is then selected for the universal instantiation of line 1:

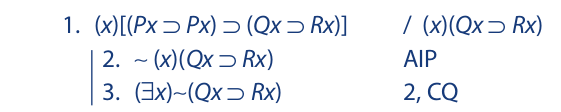
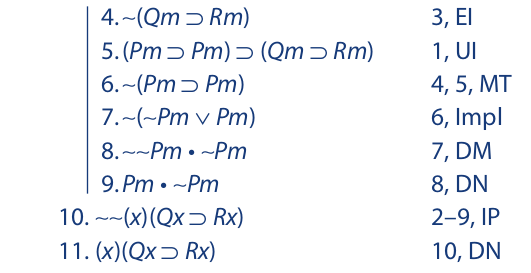
The next example has a particular statement for its conclusion:

Since indirect proof sequences are indented, they are subject to the same restriction on universal generalization as are conditional sequences. The following proof, which is similar to the previous one, violates this restriction because the instantial variable x is free in the first line of the sequence. The violation (line 4) allows a universal statement to be drawn for the conclusion, whereas only a particular statement is legitimate (as in the prior example):

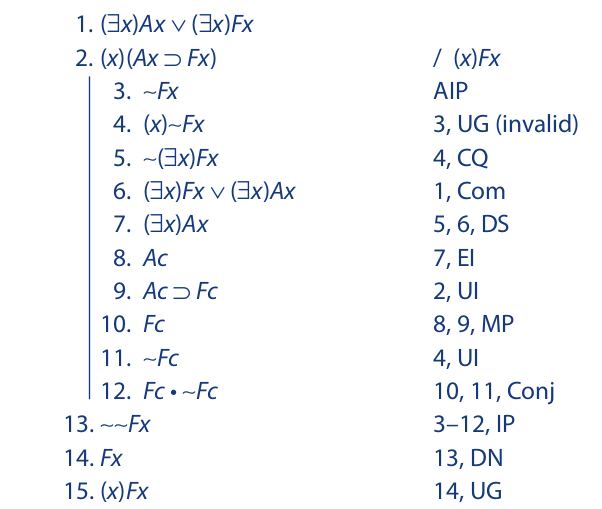
To see that this argument is indeed invalid, let Ax stand for “x is an apple” and Fx for “x is a fruit.” The first premise then reads “Either an apple exists or a fruit exists” (which is true), and the second premise reads “All apples are fruits” (which is also true). The conclusion, however, reads “Everything in the universe is a fruit,” and this, of course, is false.

As in propositional logic, conditional and indirect sequences in predicate logic may include each other. The following proof uses an indirect sequence within the scope of a conditional sequence.

The conditional sequence begins, as usual, by assuming the antecedent of the conditional statement to be derived. The objective, then, is to derive the consequent. This is accomplished by the indirect sequence, which begins with the negation of the consequent and ends (line 14) with a contradiction.

 

8.5 Proving Invalidity

In the previous chapter we saw that natural deduction could not be used with any facility to prove invalidity in propositional logic. The same thing can be said about natural deduction in predicate logic. But in predicate logic there is no simple and automatic technique such as truth tables or Venn diagrams to fall back on. However, there are two methods for proving invalidity in predicate logic that are just as effective as these other techniques, even though they may not be as convenient. One is the method used in Chapter 1 to prove the invalidity of various kinds of syllogisms—namely, the counterexample method. The other is what we will call the finite universe method. Both appeal to the basic idea underlying most proofs of invalidity: Any argument is proved invalid if it is shown that it is possible for it to have true premises and a false conclusion. Both methods are aimed at disclosing a situation that fulfills this requirement.

 

Counterexample Method

Recall from Chapter 1 that applying the counterexample method consists in finding a substitution instance of a given invalid argument form (or, equally well, a given invalid symbolized argument) that has actually true premises and a false conclusion. For an example of its use, consider the following invalid symbolized argument:

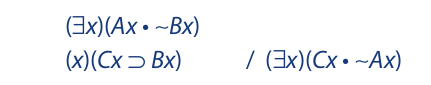
In creating a substitution instance, beginning with the conclusion is often easiest. The conclusion is translated as “Some C are not A.” Thus, to make this statement false, we need to find an example of a class (for C) that is included in another class (for A). Cats and animals will serve this purpose. A little ingenuity provides us with the following substitution instance:

When we produce such a substitution instance, the premises must turn out to be indisputably true in the actual world, and the conclusion indisputably false. Statements involving the names of animal classes are convenient for this purpose, because everyone agrees about cats, dogs, mammals, fish, and so on. Also, several different substitution instances can usually be produced that suffice to prove the argument invalid. Finally, any substitution instance that results in true premises and a true conclusion (or any arrangement other than true premises and false conclusion) proves nothing.

Here is an example of an invalid symbolized argument that includes a singular statement:

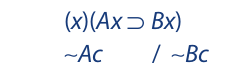
This argument form commits the fallacy of denying the antecedent. Producing a substitution instance is easy:

In selecting the name of an individual for the second premise, it is again necessary to pick something that everyone agrees on. Since everyone knows that Lassie is a dog, this name serves our purpose. But if we had selected some other name, such as Trixie or Ajax, this would hardly suffice, because there is no general agreement as to what these names denote.

Here is a slightly more complex example:

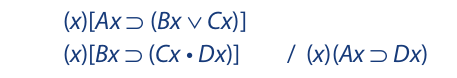
A little ingenuity produces the following substitution instance:

The counterexample method is effective with most fairly simple invalid arguments in predicate logic. Since its application depends on the ingenuity of the user, however, it is not particularly well suited for complex arguments. For those, the finite universe method is probably a better choice.

 

Finite Universe Method

The finite universe method can be used to establish the invalidity of any invalid argument expressed in terms of a single variable. It depends on the idea that a valid argument remains valid no matter how things in the actual universe might be altered. Accordingly, if we are given a valid argument, then that argument remains valid if it should happen that the universe is contracted so that it contains only a single member. On the other hand, if it should turn out that an argument has true premises and false conclusion in a universe consisting of only one or a few members, then that argument has been proved invalid.

To see how this method works, we need to understand what happens to the meaning of universal and particular statements when the universe is shrunk in size. Accordingly, let us imagine that the universe contains only one thing instead of the billions of things that it actually contains. Let us name that one thing “Abigail.” The statement “Everything in the universe is perfect” is then equivalent to “Abigail is perfect” (because Abigail is all that there is), and the statement “Something in the universe is perfect” is also equivalent to “Abigail is perfect” (because Abigail is that “something”).

To represent this equivalence symbolically, we need a new metalogical symbol that asserts that the expressions on either side of it necessarily have the same truth value given a universe of a designated size. Although this equivalence bears a close resemblance to logical equivalence, it is not identical to it, because logical equivalence holds independently of any alterations in the universe. The concept that we need to represent is a kind of conditional logical equivalence. Accordingly, we will select the double colon superscribed with a “c” (for “conditional”). For our purpose here, ::c has the same effect as ::. Using the former symbol, we have for a universe consisting of one member:

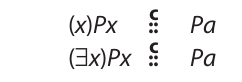
Proceeding, if we imagine that the universe contains exactly two things—let us name them “Abigail” and “Beatrice”—the statement “Everything in the universe is perfect” is equivalent to “Abigail is perfect and Beatrice is perfect.” On the other hand, the statement “Something in the universe is perfect” is equivalent to “Abigail is perfect or Beatrice is perfect” (because “some” means at least one). In other words, the universal statement is equivalent to a conjunction of singular statements, and the particular statement is equivalent to a disjunction of singular statements. In symbols:

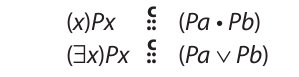
If the universe is increased to three—let us call the new member “Charmaine”—we have

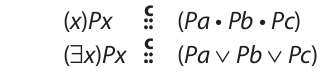
This equivalence continues indefinitely as more and more members are added to the universe.

Extending this treatment to the more typical kinds of universal and particular statements, we have, for a universe of three:

For expressions involving combinations of quantified statements, each of the component statements is translated separately and the resulting statement groups are linked together by means of the connective appearing in the original statement. Here are two examples for a universe of three:

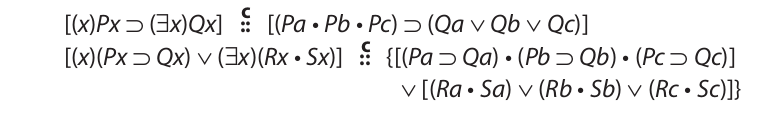
The method for proving an argument invalid consists in translating the premises and conclusion into singular statements, as per the above examples, and then testing the result with an indirect truth table (see Section 6.5). First a universe of one is tried. If it is possible for the premises to be true and the conclusion false in this universe, the argument is immediately identified as invalid. If, on the other hand, a contradiction results from this assumption, a universe of two is then tried. If, in this second universe, it is possible for the premises to be true and the conclusion false, the argument is invalid. If not, a universe of three is tried, and so on.

Consider the following symbolized argument:

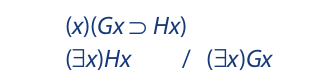
For a universe having one member—call this member “Abigail”—the argument translates into

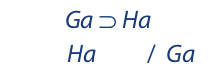
Testing with an indirect truth table, we have

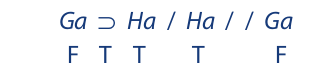
Because it is possible for the premises to be true and the conclusion false, the argument is invalid. Another example:

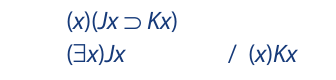
For a universe having one member, the indirect truth table is as follows:

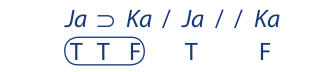
Since it is impossible for the premises to be true and the conclusion false for this universe, we try a universe having two members, a and b:

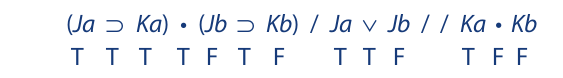
Here is an example involving compound statements:

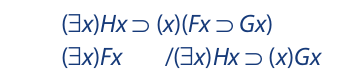
The indirect truth table for a universe having one member is as follows:

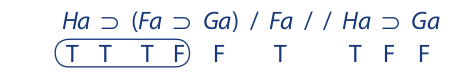
A contradiction results, so we try a universe having two members. The resulting indirect truth table proves the argument invalid:

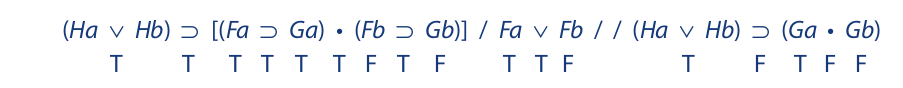
The next example involves singular statements:

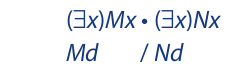
The second premise asserts that something named d is an M. For this argument, the assumption that the universe contains only one member entails that this one member is named d. Here is the indirect truth table for such a universe:

When the universe is expanded to include two members, we are free to give any name we wish to the second member. Let us call it e. The resulting indirect truth table, which follows, shows that the argument is invalid. Notice that the second premise and the conclusion remain the same:

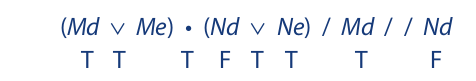
The basic concept behind this method of proving invalidity rests on the fact that a valid argument is valid in all possible universes. Consequently, if an argument fails in a universe consisting of one, two, or any number of members, it is invalid.

While this method is intended primarily for proving arguments invalid, theoretically it can also be used to prove arguments valid. Several years ago a theorem was proved to the effect that an argument that does not fail in a universe of 2n members, where n designates the number of different predicates, is valid.* According to this theorem, establishing the validity of an argument containing two different predicates requires a universe having four members, establishing the validity of an argument containing three different predicates requires a universe having eight members, and so on. For most arguments, however, a universe having four members is unwieldy at best, and a universe having eight members approaches the impossible (although a computer could handle it easily). Thus, while this method is usually quite convenient for proving invalidity, practical limitations impede its usefulness in establishing validity.

 

8.6 Relational Predicates and Overlapping Quantifiers

Even the logical machinery developed thus far is not adequate for deriving the conclusions of a number of arguments. Consider, for example, the following:

The first argument involves a relation—the relation of ownership—and we have yet to see how relations can be dealt with. The second argument, while not involving any relations, involves a quantifier that overlaps another quantifier. In this section the apparatus of predicate logic will be extended to cover examples such as these.

The predicates we have used thus far are called monadic predicates, or one-place predicates, because they are used to assign an attribute to individual things. A relational predicate (or relation) is a predicate that is used to establish a connection between or among individuals.

Relations occur in varying degrees of complexity, depending on the number of individuals related. The simplest, called binary (or dyadic) relations, establish a connection between two individuals. Some examples are the relation of being taller than, as expressed in the statement “Steve is taller than David,” and the relation of being a friend, as expressed in “Sylvia is a friend of Olivia.” Trinary (or triadic) relations establish a connection among three individuals: for example, the relation of being between, as in “St. Louis is between Chicago and New Orleans,” and the relation of reading something to someone, as in “George read Othello to Madeline.” Quaternary (or tetradic) relations link four individuals together—for example, the relation of reading something to someone at a certain time, as in “George read Othello to Madeline on Thursday.” The complexity increases until we have what are called n-ary (or n-adic) relations, which link n things together. In this section we will restrict our attention to binary relations.

 

Translating Relational Statements

Relations are symbolized like other predicates except that two lowercase letters, representing the two related individuals, are written to the immediate right of the uppercase letter representing the relation. Here are some examples of relational statements involving specifically named individuals:

Notice that the order in which the lowercase letters are listed often makes a difference. If the third statement were translated Tew, the symbolic statement would read “The Empire State Building is taller than the Willis Tower,” which is false. Quantifiers are attached to relational predicates in the same way they are to monadic predicates. Some examples of relational statements involving quantifiers are as follows:

The last four statements involve overlapping quantifiers. We may read these symbols as follows:

Applying this phraseology to the last statement given, for example, we have “There exists an x such that for all y, x is different from y”—which is simply another way of saying “Something is different from everything.”

When two quantifiers of the same sort appear adjacent to each other, the order in which they are listed is not significant. In other words, the statement (x)(y)Dxy is logically equivalent to (y)(x)Dxy, and (∃x)(∃y)Dxy is logically equivalent to (∃y)(∃x)Dxy. A little reflection on the meaning of these statements should justify this equivalence. But when different quantifiers appear adjacent to each other, the order does make a difference, sometimes even when the statement function is nonrelational. Accordingly, (x)(∃y)Dxy is not logically equivalent to (∃y)(x)Dxy. This fact can be seen more clearly in terms of a different example. If Lxy means “x loves y” and we imagine the universe of discourse restricted to people, then (x)(∃y)Lxy means “Everyone loves someone (or other),” while (∃y)(x)Lxy means “There is someone whom everyone loves.” Clearly these two statements are not equivalent.

Relational predicates can be combined with ordinary predicates to translate statements having varying degrees of complexity. In the examples that follow, Px means “x is a person.” The meaning of the other predicates should be clear from the context:

The same general rule applies in translating these statements as applies in translating any other statement in predicate logic: Universal quantifiers go with implications and existential quantifiers go with conjunctions. Every one of the eight symbolic expressions given here follows this rule. For example, in the first statement, both quantifiers are universal and both operators are horseshoes. In the second statement, the main quantifier is existential and the subordinate quantifier universal; accordingly, the main operator is a dot and the subordinate operator is a horseshoe. Among these statements, the sixth is the most complex. The symbolic translation of this statement reads, “For all x, if x is a person and there exists a y such that y is a person and x cares for y, then there exists a z such that z is a person and z cares for x.” It should be clear that this is simply another way of expressing the original English statement.

Another important rule to keep in mind when translating statements of this kind is that every variable must be bound by some quantifier. If a variable is left dangling outside the scope of its intended quantifier, the translation is defective. For example, if the second statement were translated (∃x)Hx • (y)(Ly ⊃ Dxy), then the x in Dxy would not be bound by the existential quantifier. As a result, the translation would be defective. Instead, in our example brackets provide for the existential quantifier to range over Dxy.

The same techniques used to translate these eight statements are also used to translate certain statements involving monadic predicates throughout. Consider the following:

Since the “it” at the end of these statements refers to one of the “good” things mentioned at the beginning, the quantifier that binds the x in Gx must also bind the x in Sx and Dx. The set of braces in the symbolic expressions ensures this.

Another point to notice regarding statements such as these is that the quantified expression inside the brackets is expressed in terms of a new variable. This procedure is essential to avoiding ambiguity. If instead of y, x had been used, the variable in this expression would appear to be bound by two different quantifiers at the same time.

In other statements, the one or more individuals mentioned at the end are not necessarily the same ones mentioned at the beginning. In such cases the quantifier that binds the individuals at the beginning should not bind those at the end. Compare the next pair of statements with those we have just considered.

In these cases the “something” at the end is not necessarily one of the “good” things mentioned at the beginning. Accordingly, the quantifier that binds the x in Gx does not range all the way to the end of the statement. Furthermore, the quantifier in question is now an existential quantifier. In the previous pair of statements the quantifier had to be universal because it ranged over the main operator, which was a horseshoe. In the new pair, however, no quantifier ranges over the implication symbol. As a result, the sense of these statements has shifted to mean “If something is good . . .”

Note that, although a different variable is used to express each of the three different components in the pair of statements just given, this is not required. Because in this case no quantifier ranges over any other quantifier, it would be perfectly appropriate to use the same variable throughout.

The next pair of statements involve relational predicates. As in the previous pair, no single quantifier ranges over the entire statement, because the individuals mentioned at the end are not necessarily the same ones mentioned at the beginning:

 

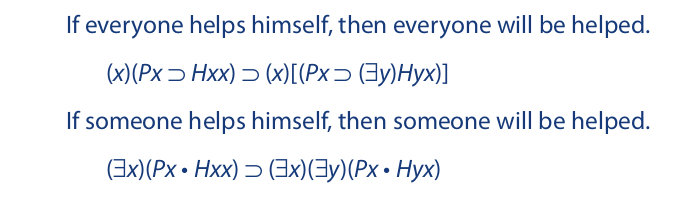
Using the Rules of Inference

Let us now see how the various quantifier rules apply to overlapping quantifiers. The change of quantifier rule is applied in basically the same way as it is with single quantifiers. The following short sequence illustrates its application:

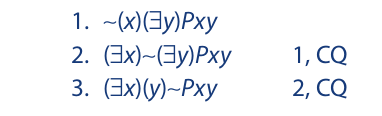
As the tilde operator is moved past a quantifier, the quantifier in question is switched for its correlative. With the exception of a restriction on universal generalization, which we will introduce presently, the instantiation and generalization rules are also used in basically the same way as they are with single quantifiers. Example:

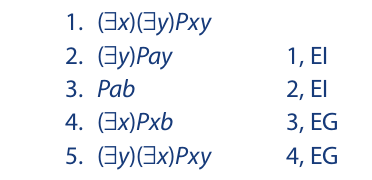
With each successive instantiation the outermost quantifier drops off. Generalization restores the quantifiers in the reverse order.

This proof demonstrates our earlier observation that the order of the quantifiers is not significant when the same kind of quantifier is used throughout. We also observed that the order does make a difference when different quantifiers appear together. Accordingly, the statement (x)(∃y)Pxy is not logically equivalent to (∃y)(x)Pxy. As the instantiation and generalization rules now stand, however, it is quite possible, with a proof similar to the one just given, to establish the logical equivalence of these two expressions. Therefore, to keep this from happening we now introduce a new restriction on universal generalization:

To see how this restriction applies, let us attempt to derive (∃x)(y)Mxy from (y)(∃x)Mxy:

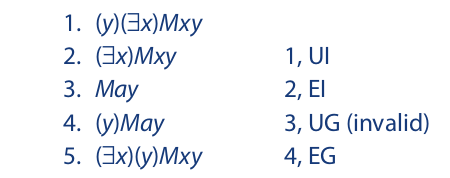
The proof fails on line 4 because the instantial variable y (that is, y) occurs free in line 3, which was obtained by EI. To see that line 4 is invalid, suppose that the universe of discourse is restricted to people, and that Mxy means “x is the mother of y.” Then line 1 asserts that for every person y there exists a person x such that x is the mother of y— which means that every person has a mother. On line 2 we select one of these people at random, and on line 3 we give the name Abigail to the mother of that person. Then on line 4 we draw the conclusion that Abigail is the mother of everyone in the universe. This inference is clearly invalid. The new restriction on UG prevents this kind of inference from being drawn.

In summary, we now have two restrictions on universal generalization. The first concerns only conditional and indirect sequences and prevents UG from occurring within the scope of such a sequence when the instantial variable is free in the first line. The second restriction concerns only arguments involving overlapping quantifiers. With these two restrictions in hand, we may now proceed to examine the use of natural deduction in arguments involving relational predicates and overlapping quantifiers. The example that follows does not include any relational predicates, but it does involve overlapping quantifiers:

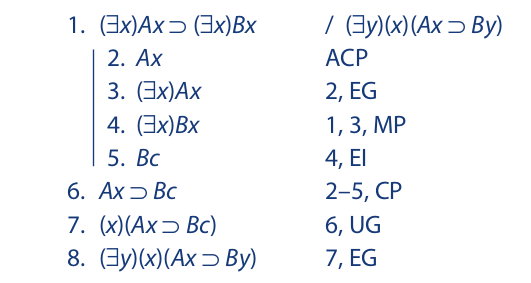
Conditional and indirect proof are used in the same way with relational predicates and overlapping quantifiers as they are with monadic predicates and nonoverlapping quantifiers. The conditional proof just given begins, as usual, by assuming the antecedent of the conclusion. When line 7 is reached, we must be careful that neither of the restrictions against universal generalization is violated. While the instantial variable x is free in the first line of the conditional sequence, line 7 does not lie within that sequence, so the first restriction is obeyed. And while line 5 was obtained by EI, x is not free in that line. Thus, the second restriction is obeyed as well.

The next proof involves a relational predicate. The proof shows that while (x)(∃y) Dxy is not logically equivalent to (∃y)(x)Dxy, it can be derived from that statement:

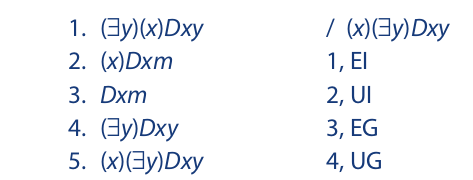
Notice that line 5 is derived by UG. Also notice that the instantial variable x occurs in line 2, which was derived by EI. However, x is not free in line 2. Thus, the second restriction on UG is obeyed.

The next example concludes with a line in which an individual is related to itself. Since there are no restrictions on universal instantiation, the procedure leading up to this line is perfectly legitimate. Notice in line 4 that tautology is used with relational predicates in the same way that it is with monadic predicates:

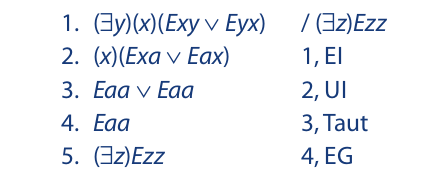
Sometimes the order in which instantiation steps are performed is critical. The following proof provides an example:

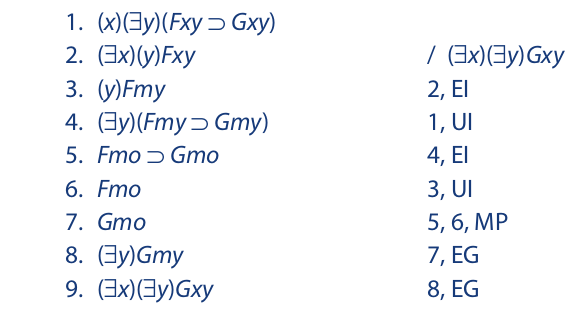
Line 2 must be instantiated before line 1 because the step introduces a new existential name. For the same reason, line 4 must be instantiated before line 3.

The next proof involves an indirect sequence. Such sequences often make use of the change of quantifier rule, as this proof illustrates:

Because line 1 cannot be instantiated, the only strategy is to derive the antecedent of the conditional with the aim of deriving the consequent via modus ponens. This is accomplished on line 11 via indirect proof. Notice on line 9 that addition is used with relational predicates in the same way that it is with monadic predicates.

A final word of caution is called for regarding universal instantiation and the two generalization rules. First, when UI is used to introduce variables into a proof, it is important that these variables end up free and that they not be captured in the process by other quantifiers. The following examples illustrate both correct and incorrect applications of this rule:

An analogous caution applies to the two generalization rules. When UG and EG are used, it is important that the instantial letter be replaced by a variable that is captured by no previously introduced quantifier and that no other variables be captured by the newly introduced quantifier. The following examples illustrate both correct and incorrect applications of this rule:

To see that the fourth example is indeed invalid, let Lxy stand for “x is larger than y,” and let the variables range over the real numbers. The statement (x)(∃y)Lxy then means that there is no smallest number—which is true. But the statement (∃x)Lxx means that there is a number that is larger than itself—which is false.

 

8.7 Identity

Many arguments in ordinary language involve a special relation called identity, and translating this relation requires special treatment. Consider, for example, the following argument:

The peculiar feature of this argument is that it involves special statements about individuals. To translate such statements, we adopt a symbol from arithmetic, the equal sign (=), to represent the identity relation. We can use this symbol to translate a large variety of statements, including simple identity statements, existential assertions about individuals, statements involving “only,” “the only,” “no . . . except,” and “all except,” and statements involving superlatives, numerical claims, and definite descriptions. After seeing how the identity relation is used to translate such statements, we will see how natural deduction is used to derive the conclusions of arguments involving identity.

 

Simple Identity Statements

The simplest statements involving identity are those asserting that a named individual is identical to another named individual. Here are some examples:

The first statement asserts that Samuel Clemens is identically the same person as Mark Twain, the second that Whoopi Goldberg is the same person as Caryn Johnson, and the third that Dr. Jekyll is the same person as Mr. Hyde. In other words, the statements claim that the names “Samuel Clemens” and “Mark Twain” designate the same person, “Whoopi Goldberg” and “Caryn Johnson” designate the same person, and so on.

To translate a negated identity statement, we simply draw a slash through the identity symbol. Thus, “Beethoven is not Mozart” is translated b ≠ m. The expression b ≠ m is just an abbreviated way of writing ∼(b = m). Here are some additional examples:

The kinds of statements we will consider next are more complicated, and to facilitate their translation a set of conventions governing conjunctions, disjunctions, and simple identity statements will now be introduced. Many of our translations will involve lengthy strings of conjunctions, such as Pm • Km • Pn • Kn. Instead of introducing parentheses and brackets into these expressions, we may simply write them as a string of conjuncts. Lengthy disjunctions may be treated the same way. In simple identity statements, the identity symbol controls only the letters to its immediate left and right. Accordingly, instead of writing (c = n) • (e = p) • (s = t), we may write c = n • e = p • s = t, and instead of writing P ⊃ (a = m), we may write P ⊃ a = m. Let us now use these conventions to translate some special kinds of statements involving identity.

 

“Only,” “The Only,” and “No . . . Except”

Section 4.7 explained that the words “only,” “the only,” and “no . . . except” signal an ordinary categorical proposition when the word that follows is a plural noun or pronoun. For example, the statement “Only relatives are invited” means simply “All invited people are relatives,” and “The only animals in this canyon are skunks” means “All animals in this canyon are skunks.” However, when the word that follows “only,” “the only,” or “no . . . except” designates an individual, something more is intended. Thus the statement “Only Nixon resigned the presidency” means (1) that Nixon resigned the presidency and (2) that if anyone resigned the presidency, that person is Nixon. Thus, the general form of such statements is that a designated individual has a stated attribute and anything having that attribute is identical to the designated individual. Here are some examples:

The first translation may be read as “Nolan Ryan has struck out 5,000 batters, and if anyone has struck out 5,000 batters, then he is identical to Nolan Ryan.” The last part of the translation ensures that no other person has struck out 5,000 batters. The second translation may be read as “Fidelio is an opera, and Fidelio was written by Beethoven, and if anything is an opera written by Beethoven, then it is identical to Fidelio.” Analogous remarks pertain to the other two statements. The third statement is equivalent to “The only nation that is a continent is Australia.”

 

“All Except”

Statements beginning with “all except” are similar to those beginning with “the only” in that they, too, assert something about a designated individual (or individuals). For example, the statement “All presidents except Washington had a predecessor” means that Washington did not have a predecessor but all other presidents did. Thus, the general form of such statements is that a designated individual lacks a stated attribute and that anything not identical to the designated individual has the stated attribute. Examples:

The first translation may be read as “Jackson Pollock is a painter who does not make sense, and every painter not identical to Jackson Pollock makes sense.”

 

Superlatives

Statements containing superlative adjectives are yet another kind of statement that can be translated by using the identity relation. These are statements asserting that, of all the members of a class, something is the largest, tallest, smallest, heaviest, lightest, and so on. To translate these statements, first give the designated item the class attribute, and then say that, if anything else has that attribute, it is somehow exceeded by the designated item. Here are some examples:

The first translation may be read as “Jupiter is a planet, and if anything is a planet and not identical to Jupiter, then Jupiter is larger than it.” The second may be read as “Ozero Baykal is a lake, and if anything is a lake and not identical to Ozero Baykal, then Ozero Baykal is deeper than it.”

 

Numerical Statements

One of the more interesting uses of the identity symbol is to translate certain kinds of numerical statements, such as “There are three people in this room.” In particular, the identity symbol allows us to translate such statements without the use of numerals. There are three types of numerical statements: those that assert a property of at most n items, those that assert a property of at least n items, and those that assert a property of exactly n items.

The first group does not assert that there actually are any items that have the stated property but only that, if there are any with the stated property, then the maximum number is n. Accordingly, for “at most” statements we use universal quantifiers. Here are some examples:

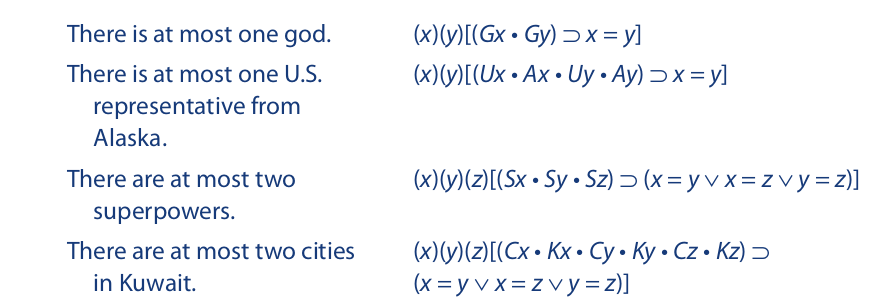
It can be seen from these examples that to translate “at most n” is to say that, if there are n + 1 items that have the stated property, then at least one of them is identical to at least one of the “others.” The result is to limit the number of such items to n. Thus, to translate “at most one,” we need two quantifiers; to translate “at most two,” we need three quantifiers; and so on. We could use this procedure to translate statements about any number of items, but because such translations become rather lengthy, this discussion is limited to statements about one or two items at most.

Unlike “at most” statements, statements that assert something about at least n items do claim that the items actually exist. Thus, to translate “at least” statements we need to use existential quantifiers. The number of quantifiers must be equal to the number of items asserted. Examples:

The first of these examples merely asserts that some city is in Monaco. Thus, it is translated without any inclusion of the identity relation. When the stated number is greater than one, however, the translation must incorporate one or more negative identity statements to ensure that the items referred to are distinct. Thus, in the second statement, if x and y should be identical, then there would actually be only one woman (at least) in Hamlet. To ensure that there are at least two distinct women, we must conjoin the assertion that x and y are not identical. Similarly, when we assert something about at least three items, we must conjoin the assertion that none of them is identical to either of the other two.

A statement about exactly n items can be seen to be the conjunction of a statement about at least n items and a statement about at most n items. For example, the statement “There are exactly three cars in the lot” means that there are at least three cars in the lot and at most three cars in the lot. Thus, a statement about exactly n items requires n existential quantifiers to ensure the existence of the items, one or more negated identity statements to ensure their distinctness (assuming n is greater than 1), and a universally quantified statement to limit the group to at most n items. Here are some examples:

 

Definite Descriptions

The last form of phraseology considered here is the definite description. A definite description is a group of words of the form “the such-and-such” that identifies an individual person, place, or thing. Here are some examples:

The first designates Henry Wadsworth Longfellow, the second the city of Lincoln, and the third Rose Fitzgerald Kennedy. Definite descriptions are like names in that they identify only one thing, but unlike names they do so by describing a situation or relationship that only that one thing satisfies.

Statements incorporating definite descriptions have given rise to disputes in logic, because alternate interpretations of such statements can lead to conflicts in truth value. Suppose, for example, we are given the statement “The queen of the United States is a woman.” Should we consider this statement to be true, because every queen is a woman, or should we consider it to be false, because there is no queen of the United States? In response to this question, most logicians today accept an interpretation of definite descriptions originally proposed by Bertrand Russell. According to this interpretation, a statement that incorporates a definite description asserts three things: an item of a certain sort exists, there is only one such item, and that item has the attribute assigned to it by the statement. If we accept this interpretation, the statement about the queen of the United States is false, because no such person exists.

Here are some additional examples with their translations:

The first translation may be read as “There is someone who invented the phonograph, and if anyone invented the phonograph, then that person is identical to the first, and the first person is an American.” The second may be read as “There is someone who wrote Middlemarch, and if anyone wrote Middlemarch, then that person is identical to the first, and the first person is a Victorian freethinker.” The third may be read as “There is someone who painted The Starry Night, and if anyone painted The Starry Night, then that person is identical to the first, and the first person is identical to Van Gogh.” 

 

Using the Rules of Inference

Now that we have seen how to translate statements involving the identity relation, let us use natural deduction to derive the conclusions of arguments that include statements of this sort. Before doing so, however, some special rules governing the identity relation must be introduced. These rules, which are collectively designated “Id,” are as follows:

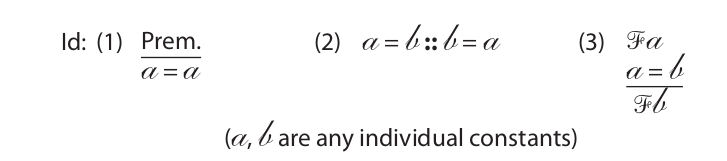
The first rule expresses the idea that anything is identical to itself; it asserts what is called the reflexive property of the identity relation. The rule allows us to insert a selfidentity statement after any premise (that is, on any line in a proof).

The second rule is a rule of replacement; it expresses what is called the symmetric property of the identity relation. It states, very simply, that the letters on either side of the equal sign can be switched. An immediate use of this rule is to prove that a ≠ b is logically equivalent to b ≠ a. Recall that a ≠ b is simply an abbreviation for ∼(a = b). If we apply the rule to the latter expression, we obtain ∼(b = a), which, in its abbreviated form, is b ≠ a.

The third rule expresses the intuitively obvious idea that, if something is true of x and x is identical to y, then that something is true of y. This rule is the basis of what is called the transitive property of identity, which allows us to infer from a = b and b = c that a = c. If we suppose that the ␂ in this rule stands for the expression “a =”, that a is b, and that b is c, then the first line of the rule reads a = b, the second line reads b = c, and the conclusion is a = c. This inference is used often in the derivation of the conclusions of arguments.

In general, the rules of inference used earlier apply to arguments containing identity statements in the same way they apply to any other arguments. Also, conditional proof and indirect proof are used in the same way. We need only note that because a and b in these rules represent only individual constants (a, b, . . . v, w) they cannot be applied to variables (x, y, z).

The following argument illustrates the first expression of the rule for identity.

If we use Bx to translate “x is a biologist,” and i for Isabel, this argument becomes

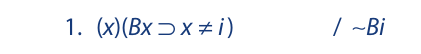
The fact that the conclusion contains i suggests that we instantiate line 1 with respect to that letter. The proof is as follows:

Line 3 comes merely from the first expression of the identity rule, which allows us to insert any self-identity statement after any premise. Thus, no numeral is included in the justification for that line. Also note that line 4 is simply another way of writing ∼∼(i = i).

Now let us return to the argument given at the beginning of this section:

If we use Fx to translate “x is my friend” and Cx to translate “x is a Canadian,” this argument may be translated as follows:

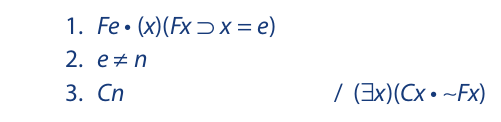
Inspecting the second line, we see a negated identity statement involving e and n. This suggests that we instantiate the universal statement in the first line with respect to n. The proof is as follows:

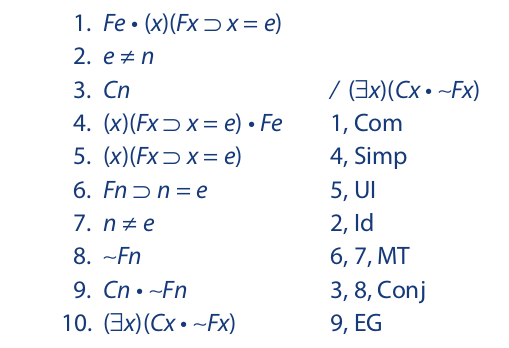
Line 7 is justified by the second rule for identity. Also, since n ≠ e is simply an abbreviation for ∼(n = e), line 8 follows directly from lines 6 and 7.

Here is another example:

The translation is as follows:

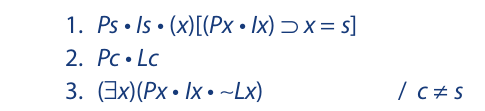
Cursory inspection reveals no easy way to obtain the conclusion. This suggests indirect proof:

As usual, the existential statement is instantiated first, then the universal. Line 11 is derived by commuting line 4 by the second rule of identity, and line 12 is derived from lines 10 and 11 by applying the third rule of identity. Line 15 is derived by substituting c in the place of a in line 14 according to the third rule of identity. The indirect sequence is discharged in line 19 in the normal way.

In arguments involving identity, especially more complicated ones, it is often difficult or impossible to see by mere inspection how to obtain the conclusion. A good general procedure is to begin with instantiation. Always instantiate the existential statements first, then the universals. When instantiating the universal statements, normally pick the letter (or one of the letters) used to instantiate the existential statement(s). If there are no existential statements, pick one of the letters appearing in the singular statements. If the conclusion is still not apparent, try indirect proof. In general, whenever the conclusion is a complicated statement, it is best to start out with indirect proof. Developing facility in proving arguments involving identity requires a little practice, but adequate skill should not take too long to acquire.