PART II: FORMAL LOGIC
Chapter 7: Natural Deduction in Propositional Logic
7.1 Rules of Implication I
Natural deduction is a method for establishing the validity of propositional type arguments that is both simpler and more enlightening than the method of truth tables. By means of this method, the conclusion of an argument is actually derived from the premises through a series of discrete steps. In this respect natural deduction resembles the method used in geometry to derive theorems relating to lines and figures; but whereas each step in a geometrical proof depends on some mathematical principle, each step in a logical proof depends on a rule of inference. This chapter will present eighteen rules of inference.
The first eight rules of inference are called rules of implication because they consist of basic argument forms whose premises imply their conclusions. The following four rules of implication should be familiar from the previous chapter:






We conclude this section with some strategies for applying the first four rules of inference.


7.2 Rules of Implication II
Four additional rules of implication are listed here.

Constructive dilemma can be understood as involving two modus ponens steps. The first premise states that if we have p then we have q, and if we have r then we have s. But since, by the second premise, we do have either p or r, it follows by modus ponens that we have either q or s. Constructive dilemma is the only form of dilemma that will be included as a rule of inference. By the rule of transposition, which will be presented in Section 7.4, any argument that is a substitution instance of the destructive dilemma form can be easily converted into a substitution instance of constructive dilemma. Destructive dilemma, therefore, is not needed as a rule of inference.

Simplification states that if two propositions are given as true on a single line, then each of them is true separately. According to the strict interpretation of the simplification rule, only the left-hand conjunct may be stated in the conclusion. Once the commutativity rule for conjunction has been presented, however (see Section 7.3), we will be justified in replacing a statement such as H • K with K • H. Once we do this, the K will appear on the left, and the appropriate conclusion is K.
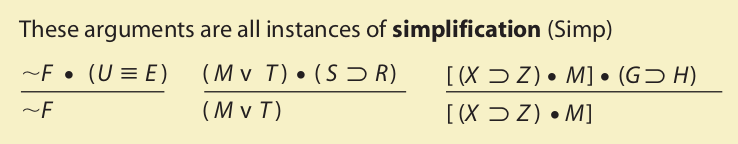
Conjunction states that two propositions—for example, H and K—asserted separately on different lines may be conjoined on a single line. The two propositions may be conjoined in whatever order we choose (either H • K or K • H) without appeal to the commutativity rule for conjunction.
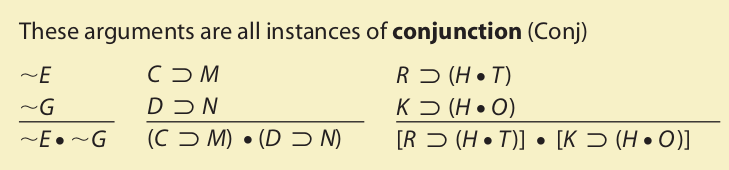
Addition states that whenever a proposition is asserted on a line by itself it may be joined disjunctively with any proposition we choose. In other words, if G is asserted to be true by itself, it follows that G ∨ H is true. This may appear somewhat puzzling at first, but once one realizes that G ∨ H is a much weaker statement than G by itself, the puzzlement should disappear. The new proposition must, of course, always be joined disjunctively (not conjunctively) to the given proposition. If G is stated on a line by itself, we are not justified in writing G • H as a consequence of addition.
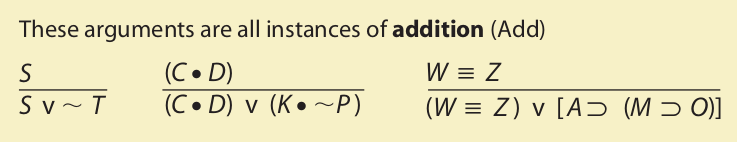
Like the previous section, this one ends with a few strategies for applying the last four rules of implication:


7.3 Rules of Replacement I
Unlike the rules of implication, which are basic argument forms, the ten rules of replacement are expressed in terms of pairs of logically equivalent statement forms, either of which can replace the other in a proof sequence. To express these rules, a new symbol, called a double colon (::), is used to designate logical equivalence. This symbol is a metalogical symbol in that it makes an assertion not about things but about symbolized statements: It asserts that the expressions on either side of it have the same truth value regardless of the truth values of their components. Underlying the use of the rules of replacement is an axiom of replacement, which asserts that within the context of a proof, logically equivalent expressions may replace each other. The first five rules of replacement are as follows:

De Morgan’s rule (named after the nineteenth-century logician Augustus De Morgan) was discussed in Section 6.1 in connection with translation. There it was pointed out that “Not both p and q” is logically equivalent to “Not p or not q,” and that “Not either p or q” is logically equivalent to “Not p and not q.” When applying De Morgan’s rule, one should keep in mind that it holds only for conjunctive and disjunctive statements (not for conditionals or biconditionals). The rule may be summarized as follows: When moving a tilde inside or outside a set of parentheses, a dot switches with a wedge and vice versa.
Commutativity asserts that the truth value of a conjunction or disjunction is unaffected by the order in which the components are listed. In other words, the component statements may be commuted, or switched for one another, without affecting the truth value. The validity of this rule should be immediately apparent. You may recall from arithmetic that the commutativity rule also applies to addition and multiplication and asserts, for example, that 3 + 5 equals 5 + 3, and that 2 × 3 equals 3 × 2. However, it does not apply to division; 2 ÷ 4 does not equal 4 ÷ 2. A similar lesson applies in logic: The commutativity rule applies only to conjunction and disjunction; it does not apply to implication.
Associativity states that the truth value of a conjunctive or disjunctive statement is unaffected by the placement of parentheses when the same operator is used throughout. In other words, the way in which the component propositions are grouped, or associated with one another, can be changed without affecting the truth value. The validity of this rule is quite easy to see, but if there is any doubt about it, it may be readily checked by means of a truth table. You may recall that the associativity rule also applies to addition and multiplication and asserts, for example, that 3 + (5 + 7) equals (3 + 5) + 7, and that 2 × (3 × 4) equals (2 × 3) × 4. But it does not apply to division: (8 ÷ 4) ÷ 2 does not equal 8 ÷ (4 ÷ 2). Analogously, in logic, the associativity rule applies only to conjunctive and disjunctive statements; it does not apply to conditional statements. Also note, when applying this rule, that the order of the letters remains unchanged; only the placement of the parentheses changes.
Distribution, like De Morgan’s rule, applies only to conjunctive and disjunctive statements. When a proposition is conjoined to a disjunctive statement in parentheses or disjoined to a conjunctive statement in parentheses, the rule allows us to put that proposition together with each of the components inside the parentheses, and also to go in the reverse direction. In the first form of the rule, a statement is distributed through a disjunction, and in the second form, through a conjunction. While the rule may not be immediately obvious, it is easy to remember: The operator that is at first outside the parentheses goes inside, and the operator that is at first inside the parentheses goes outside. Note also how distribution differs from commutativity and associativity. The latter two rules apply only when the same operator (either a dot or a wedge) is used throughout a statement. Distribution applies when a dot and a wedge appear together in a statement.
Double negation is fairly obvious and needs little explanation. The rule states simply that pairs of tildes immediately adjacent to one another may be either deleted or introduced without affecting the truth value of the statement.
There is an important difference between the rules of implication, treated in the first two sections of this chapter, and the rules of replacement. The rules of implication derive their name from the fact that each is a simple argument form in which the premises imply the conclusion. To be applicable in natural deduction, certain lines in a proof must be interpreted as substitution instances of the argument form in question. Stated another way, the rules of implication are applicable only to whole lines in a proof. For example, step 3 in the following proof is not a legitimate application of modus ponens, because the first premise in the modus ponens rule is applied to only a part of line 1.

The rules of replacement, on the other hand, are not rules of implication but rules of logical equivalence. Since, by the axiom of replacement, logically equivalent statement forms can always replace one another in a proof sequence, the rules of replacement can be applied either to a whole line or to any part of a line. Step 2 in the following proof is a quite legitimate application of De Morgan’s rule, even though the rule is applied only to the consequent of line 1:
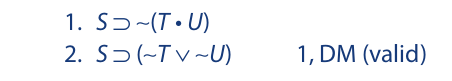
Another way of viewing this distinction is that the rules of implication are “oneway” rules, whereas the rules of replacement are “two-way” rules. The rules of implication allow us to proceed only from the premise lines of a rule to the conclusion line, but the rules of replacement allow us to replace either side of an equivalence expression with the other side.
Application of the first five rules of replacement may now be illustrated. Consider the following argument:
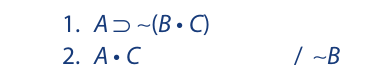
Examining the premises, we find B in the consequent of line 1. This leads us to suspect that the conclusion can be derived via modus ponens. If this is correct, the tilde would then have to be taken inside the parentheses via De Morgan’s rule and the resulting ∼C eliminated by disjunctive syllogism. The following completed proof indicates that this strategy yields the anticipated result:

The rationale for line 6 is to get C on the left side so that it can be separated via simplification. Similarly, the rationale for line 9 is to get ∼C on the left side so that it can be eliminated via disjunctive syllogism. Line 8 is required because, strictly speaking, the negation of ∼C is ∼∼C—not simply C. Thus, C must be replaced with ∼∼C to set up the disjunctive syllogism. If your instructor permits it, you can combine commutativity and double negation with other inferences on a single line, as the following shortened proof illustrates. However, we will avoid this practice throughout the remainder of the book.

Here are some strategies for applying the first five rules of replacement. Most of them show how these rules may be used together with other rules.



7.4 Rules of Replacement II
The remaining five rules of replacement are as follows:

Transposition asserts that the antecedent and consequent of a conditional statement may switch places if and only if tildes are inserted before both or tildes are removed from both. The rule is fairly easy to understand and is easily proved by a truth table.
Material implication is less obvious than transposition, but it can be illustrated by substituting actual statements in place of the letters. For example, the statement“If you bother me, then I’ll punch you in the nose” (B ⊃ P) is logically equivalent to “Either you stop bothering me or I’ll punch you in the nose” (∼B ∨ P). The rule states that a horseshoe may be replaced by a wedge if the left-hand component is negated, and the reverse replacement is allowed if a tilde is deleted from the left-hand component.
Material equivalence has two formulations. The first is the same as the definition of material equivalence given in Section 6.1. The second formulation is easy to remember through recalling the two ways in which p ≡ q may be true. Either p and q are both true or p and q are both false. This, of course, is the meaning of [(p • q) ∨ (∼p • ∼q)].
Exportation is also fairly easy to understand. It asserts that the statement “If we have both p and q, then we have r” is logically equivalent to “If we have p, then if we have q, then we have r.” As an illustration of this rule, the statement “If Bob and Sue told the truth, then Jim is guilty” is logically equivalent to “If Bob told the truth, then if Sue told the truth, then Jim is guilty.”
Tautology, the last rule introduced in this section, is obvious. Its effect is to eliminate redundancy in disjunctions and conjunctions.
This section ends with some strategies that show how the last five rules of replacement can be used together with various other rules.



7.5 Conditional Proof
Conditional proof is a method for deriving a conditional statement (either the conclusion or some intermediate line) that offers the usual advantage of being both shorter and simpler to use than the direct method. Moreover, some arguments have conclusions that cannot be derived by the direct method, so some form of conditional proof must be used on them. The method consists of assuming the antecedent of the required conditional statement on one line, deriving the consequent on a subsequent line, and then “discharging” this sequence of lines in a conditional statement that exactly replicates the one that was to be obtained.
Any argument whose conclusion is a conditional statement is an immediate candidate for conditional proof. Consider the following example:
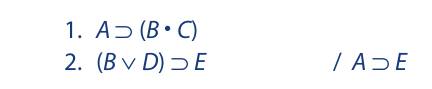
Using the direct method to derive the conclusion of this argument would require a proof having at least twelve lines, and the precise strategy to be followed in constructing it might not be immediately obvious. Nevertheless, we need only give cursory inspection to the argument to see that the conclusion does indeed follow from the premises. The conclusion states that if we have A, we then have E. Let us suppose, for a moment, that we do have A. We could then derive B • C from the first premise via modus ponens. Simplifying this expression we could derive B, and from this we could get B ∨ D via addition. E would then follow from the second premise via modus ponens. In other words, if we assume that we have A, we can get E. But this is exactly what the conclusion says. Thus, we have just proved that the conclusion follows from the premises.
The method of conditional proof consists of incorporating this simple thought process into the body of a proof sequence. A conditional proof for this argument requires only eight lines and is substantially simpler than a direct proof:

Lines 3 through 7 are indented to indicate their hypothetical character: They all depend on the assumption introduced in line 3 via ACP (assumption for conditional proof). These lines, which constitute the conditional proof sequence, tell us that if we assume A (line 3), we can derive E (line 7). In line 8 the conditional sequence is discharged in the conditional statement A ⊃ E, which simply reiterates the result of the conditional sequence. Since line 8 is not hypothetical, it is written adjacent to the original margin, under lines 1 and 2. A vertical line is added to the conditional sequence to emphasize the indentation.
The first step in constructing a conditional proof is to decide what should be assumed on the first line of the conditional sequence. While any statement whatsoever can be assumed on this line, only the right statement will lead to the desired result. The clue is always provided by the conditional statement to be obtained in the end. The antecedent of this statement is what must be assumed. For example, if the statement to be obtained is (K • L) ⊃ M, then K • L should be assumed on the first line. This line is always indented and tagged with the designation “ACP.” Once the initial assumption has been made, the second step is to derive the consequent of the desired conditional statement at the end of the conditional sequence. To do this, we simply apply the ordinary rules of inference to any previous line in the proof (including the assumed line), writing the result directly below the assumed line. The third and final step is to discharge the conditional sequence in a conditional statement. The antecedent of this conditional statement is whatever appears on the first line of the conditional sequence, and the consequent is whatever appears on the last line. For example, if A ∨ B is on the first line and C • D is on the last, the sequence is discharged by (A ∨ B) ⊃ (C • D). This discharging line is always written adjacent to the original margin and is tagged with the designation “CP” (conditional proof) together with the numerals indicating the first through the last lines of the sequence.
Conditional proof can also be used to derive a line other than the conclusion of an argument. The following proof, which illustrates this fact, incorporates two conditional sequences one after the other within the scope of a single direct proof:

The first conditional proof sequence gives us G ⊃ H, and the second J ⊃ K. These two lines are then conjoined and used together with line 3 to set up a constructive dilemma, from which the conclusion is derived.
This proof sequence provides a convenient opportunity to introduce an important rule governing conditional proof. The rule states that after a conditional proof sequence has been discharged, no line in the sequence may be used as a justification for a subsequent line in the proof. If, for example, line 5 in the proof just given were used as a justification for line 9 or line 12, this rule would be violated, and the corresponding inference would be invalid. Once the conditional sequence is discharged, it is sealed off from the remaining part of the proof. The logic behind this rule is easy to understand. The lines in a conditional sequence are hypothetical in that they depend on the assumption stated in the first line. Because no mere assumption can provide any genuine support for anything, neither can any line that depends on such an assumption. When a conditional sequence is discharged, the assumption on which it rests is expressed as the antecedent of a conditional statement. This conditional statement can be used to support subsequent lines because it makes no claim that its antecedent is true. The conditional statement merely asserts that if its antecedent is true, then its consequent is true, and this, of course, is what has been established by the conditional sequence from which it is obtained.
Just as a conditional sequence can be used within the scope of a direct proof to derive a desired statement, one conditional sequence can be used within the scope of another to derive a desired statement. The following proof provides an example:

The rule introduced in connection with the previous example applies unchanged to examples of this sort. No line in the sequence 5–8 could be used to support any line subsequent to line 9, and no line in the sequence 3–10 could be used to support any line subsequent to line 11. Lines 3 or 4 could, of course, be used to support any line in the sequence 5–8.
One final reminder regarding conditional proof is that every conditional proof must be discharged. It is absolutely improper to end a proof on an indented line. If this rule is ignored, any conclusion one chooses can be derived from any set of premises. The following invalid proof illustrates this mistake:

7.6 Indirect Proof
Indirect proof is a technique similar to conditional proof that can be used on any argument to derive either the conclusion or some intermediate line leading to the conclusion. It consists of assuming the negation of the statement to be obtained, using this assumption to derive a contradiction, and then concluding that the original assumption is false. This last step, of course, establishes the truth of the statement to be obtained. The following proof sequence uses indirect proof to derive the conclusion:

The indirect proof sequence (lines 3–10) begins by assuming the negation of the conclusion. Since the conclusion is a negated statement, it shortens the proof to assume A instead of ∼∼A. This assumption, which is tagged “AIP” (assumption for indirect proof), leads to a contradiction in line 10. Since any assumption that leads to a contradiction is false, the indirect sequence is discharged (line 11) by asserting the negation of the assumption made in line 3. This line is then tagged with the designation “IP” (indirect proof) together with the numerals indicating the scope of the indirect sequence from which it is obtained.
Indirect proof can also be used to derive an intermediate line leading to the conclusion. Example:

The indirect proof sequence begins with the assumption of F (line 8), leads to a contradiction (line 14), and is discharged (line 15) by asserting the negation of the assumption. One should consider indirect proof whenever a line in a proof appears difficult to obtain.
As with conditional proof, when an indirect proof sequence is discharged, no line in the sequence may be used as a justification for a subsequent line in the proof. In reference to the last proof, this means that none of the lines 8–14 could be used as a justification for any of the lines 16–19. Occasionally, this rule requires certain priorities in the derivation of lines. For example, for the purpose of deriving the contradiction, lines 6 and 7 could have been included as part of the indirect sequence. But this would not have been advisable, because line 7 is needed as a justification for line 16, which lies outside the indirect sequence. If lines 6 and 7 had been included within the indirect sequence, they would have had to be repeated after the sequence had been discharged to allow ∼K to be derived on a line outside the sequence.
Just as a conditional sequence may be constructed within the scope of another conditional sequence, so a conditional sequence may be constructed within the scope of an indirect sequence, and, conversely, an indirect sequence may be constructed within the scope of either a conditional sequence or another indirect sequence. The next example illustrates the use of an indirect sequence within the scope of a conditional sequence:
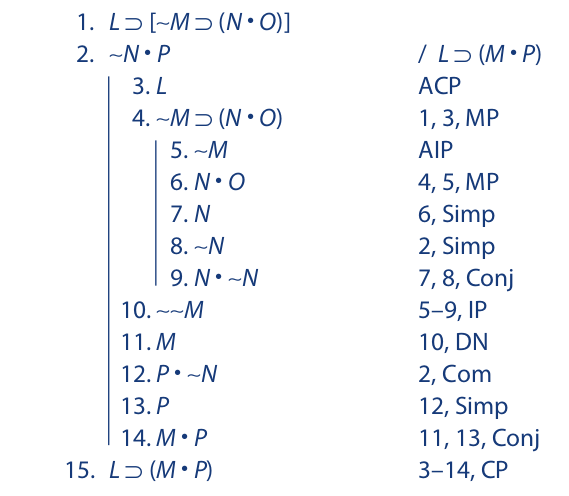
The indirect sequence (lines 5–9) is discharged (line 10) by asserting the negation of the assumption made in line 5. The conditional sequence (lines 3–14) is discharged (line 15) in the conditional statement that has the first line of the sequence as its antecedent and the last line as its consequent.
Indirect proof provides a convenient way for proving the validity of an argument having a tautology for its conclusion. In fact, the only way in which the conclusion of many such arguments can be derived is through either conditional or indirect proof.
For the following argument, indirect proof is the easier of the two:
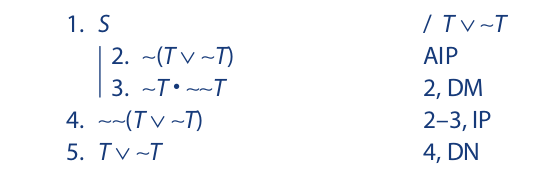
Here is another example of an argument having a tautology as its conclusion. In this case, since the conclusion is a conditional statement, conditional proof is the easier alternative:

The similarity of indirect proof to conditional proof may be illustrated by returning to the first example presented in this section. In the proof that follows, conditional proof—not indirect proof—is used to derive the conclusion:

This example illustrates how a conditional proof can be used to derive the conclusion of any argument, whether or not the conclusion is a conditional statement. Simply begin by assuming the negation of the conclusion, derive contradictory statements on separate lines, and use these lines to set up a disjunctive syllogism yielding the negation of the assumption as the last line of the conditional sequence. Then, discharge the sequence and use tautology to derive the negation of the assumption outside the sequence.
Indirect proof can be viewed as a variety of conditional proof in that it amounts to a modification of the way in which the indented sequence is discharged, resulting in an overall shortening of the proof for many arguments. The indirect proof for the argument just given is repeated as follows, with the requisite changes noted in the margin:

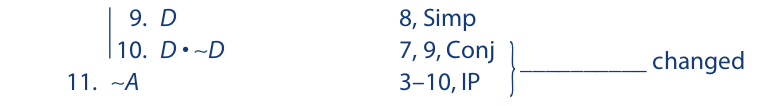
The reminder at the end of the previous section regarding conditional proof pertains to indirect proof as well: It is essential that every indirect proof be discharged. No proof can be ended on an indented line. If this rule is ignored, indirect proof, like conditional proof, can produce any conclusion whatsoever. The following invalid proof illustrates such a mistake:

7.7 Proving Logical Truths
Both conditional and indirect proof can be used to establish the truth of a logical truth (tautology). Tautological statements can be treated as if they were the conclusions of arguments having no premises. Such a procedure is suggested by the fact that any argument having a tautology for its conclusion is valid regardless of what its premises are. As we saw in the previous section, the proof for such an argument does not use the premises at all but derives the conclusion as the exclusive consequence of either a conditional or an indirect sequence. Using this strategy for logical truths, we write the statement to be proved as if it were the conclusion of an argument, and we indent the first line in the proof and tag it as being the beginning of either a conditional or an indirect sequence. In the end, this sequence is appropriately discharged to yield the desired statement form.
Tautologies expressed in the form of conditional statements are most easily proved via a conditional sequence. The following example uses two such sequences, one within the scope of the other:

Notice that line 6 restores the proof to the original margin—the first line is indented because it introduces the conditional sequence.
Here is a proof of the same statement using an indirect proof. The indirect sequence begins, as usual, with the negation of the statement to be proved:

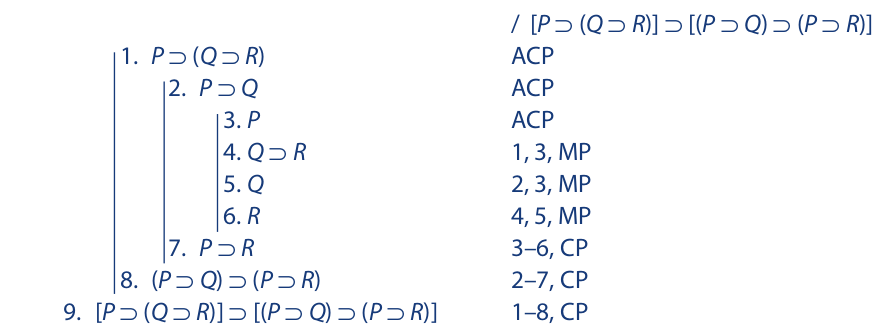
More complex conditional statements are proved by merely extending the technique used in the first proof. In the following proof, notice how each conditional sequence begins by asserting the antecedent of the conditional statement to be derived:
Tautologies expressed as equivalences are usually proved using two conditional sequences, one after the other. Example:





 浙公网安备 33010602011771号
浙公网安备 33010602011771号