PART II: FORMAL LOGIC
Chapter 5: Categorical Syllogisms
5.1 Standard Form, Mood, and Figure
In the general sense of the term, a syllogism is a deductive argument consisting of two premises and one conclusion. Provisionally we will define a categorical syllogism as a syllogism consisting of three categorical propositions and containing a total of three different terms, each of which appears twice in distinct propositions. (We will give a more precise definition shortly.) The following argument is a categorical syllogism:

Each of the three terms in a categorical syllogism has its own name depending on its position in the argument. The major term, by definition, is the predicate of the conclusion, and the minor term is the subject of the conclusion. The middle term, which provides the middle ground between the two premises, is the one that occurs once in each premise and does not occur in the conclusion. Thus, for the argument just given, the major term is “soldiers,” the minor term is “traitors,” and the middle term is “patriots.”
The premises of a categorical syllogism also have their own names. The major premise, by definition, is the one that contains the major term, and the minor premise is the one that contains the minor term. Thus, in the syllogism just given the major premise is “All soldiers are patriots,” and the minor premise is “No traitors are patriots.”
Now that we are supplied with these definitions, we may proceed to the idea of standard form. A standard-form categorical syllogism is one that meets the following four conditions:
1. All three statements are standard-form categorical propositions.
2. The two occurrences of each term are identical.
3. Each term is used in the same sense throughout the argument.
4. The major premise is listed first, the minor premise second, and the conclusion last.
The first condition requires that each statement have a proper quantifier, subject term, copula, and predicate term. The second condition is clear. The third rules out the possibility of equivocation. For example, if a syllogism containing the word “men” used that term in the sense of human beings in one statement and in the sense of male human beings in another statement, the syllogism would really contain more than three terms and would therefore not be in standard form. Finally, the fourth condition merely requires that the three statements be listed in the right order.
The syllogism about soldiers is in standard form because all four conditions are fulfilled. However, the following syllogism is not in standard form, because the fourth condition is violated:

To put this syllogism into standard form the order of the premises must be reversed. The major premise (the one containing “masterpieces,” which is the predicate term in the conclusion) must be listed first, and the minor premise (the one containing “paintings,” which is the subject term in the conclusion) must be listed second.
Now that we have a definition of standard-form categorical syllogism, we can give a more precise definition of categorical syllogism. A categorical syllogism is a deductive argument consisting of three categorical propositions that is capable of being translated into standard form. For an argument to qualify as a categorical syllogism, all three statements need not be standard-form categorical propositions; but if they are, the analysis is greatly simplified. For this reason, all of the syllogisms presented in the first four sections of this chapter will consist of statements that are in standard form. In later sections, techniques will be developed for translating non-standard form syllogisms into equivalent arguments that are in standard form.
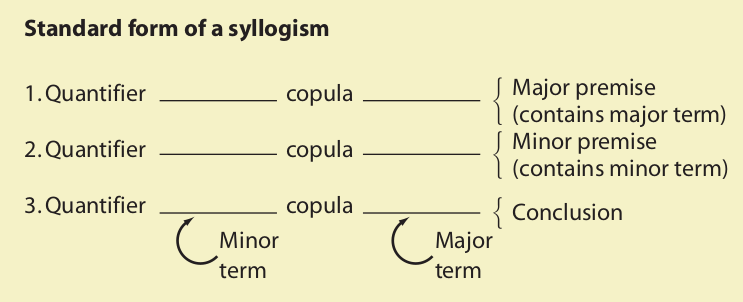
After a categorical syllogism has been put into standard form, its validity or invalidity may be determined through mere inspection of the form. The individual form of a syllogism consists of two factors: mood and figure. The mood of a categorical syllogism consists of the letter names of the propositions that make it up. For example, if the major premise is an A proposition, the minor premise an O proposition, and the conclusion an E proposition, the mood is AOE. To determine the mood of a categorical syllogism, one must first put the syllogism into standard form; the letter name of the statements may then be noted to the side of each. The mood of the syllogism is then designated by the order of these letters, reading the letter for the major premise first, the letter for the minor premise second, and the letter for the conclusion last.
The figure of a categorical syllogism is determined by the location of the two occurrences of the middle term in the premises. Four different arrangements are possible. If we let S represent the subject of the conclusion (minor term), P the predicate of the conclusion (major term), and M the middle term, and leave out the quantifiers and copulas, the four possible arrangements may be illustrated as follows:
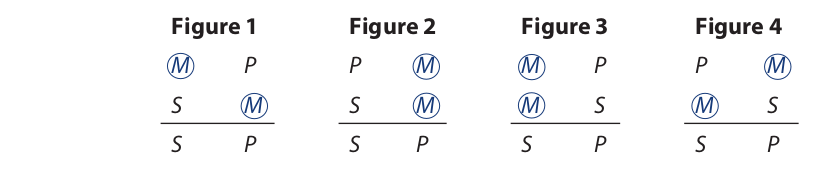
In the first figure the middle term is top left, bottom right; in the second, top right, bottom right, and so on. Example:

This syllogism is in standard form. The mood is EIO and the figure is four. The form of the syllogism is therefore designated as EIO-4.
To remember how the four figures are defined, imagine the four possible arrangements of the middle term as depicting the outline of a shirt collar:
Since there are four kinds of categorical propositions and there are three categorical propositions in a categorical syllogism, there are 64 possible moods (4 × 4 × 4 = 64). And since there are four different figures, there are 256 different forms of categorical syllogisms (4 × 64 = 256).
Once the mood and figure of a syllogism is known, the validity of the syllogism can be determined by checking the mood and figure against a list of valid syllogistic forms. To do this, first adopt the Boolean standpoint and see if the syllogism’s form appears in the following table of unconditionally valid forms. If it does, the syllogism is valid from the Boolean standpoint. In other words, it is valid regardless of whether its terms denote actually existing things.

If the syllogism does not appear on the list of unconditionally valid forms, then adopt the Aristotelian standpoint and see if the syllogism’s form appears in the following table of conditionally valid forms. If it does, the syllogism is valid from the Aristotelian standpoint on condition that a certain term (the “critical” term) denotes actually existing things. The required condition is stated in the last column.
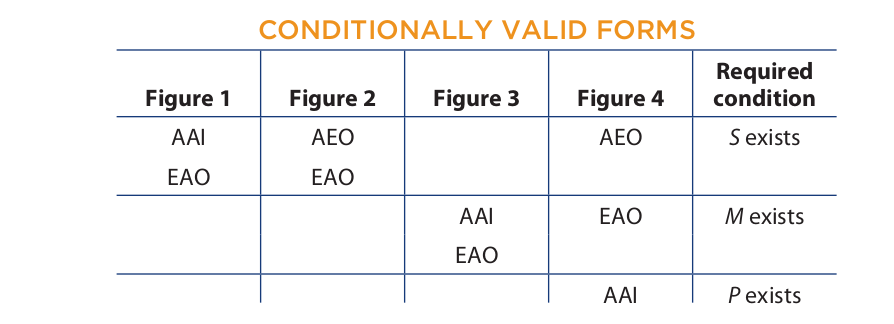
For example, the AAI-1 is valid from the Aristotelian standpoint if the subject of the conclusion (the minor term) denotes actually existing things. The EAO-3 is valid if the middle term denotes actually existing things. Thus, if we are given an AAI-1 syllogism and the minor term is “cats,” then the syllogism is valid from the Aristotelian standpoint. But if the minor term is “unicorns,” then the syllogism is invalid. On the other hand, if the minor term is “students who failed the exam” and we are not certain if there are any such students, then the syllogism is conditionally valid.
The relationship between the Aristotelian standpoint and the Boolean standpoint is illustrated in the following bar graph:
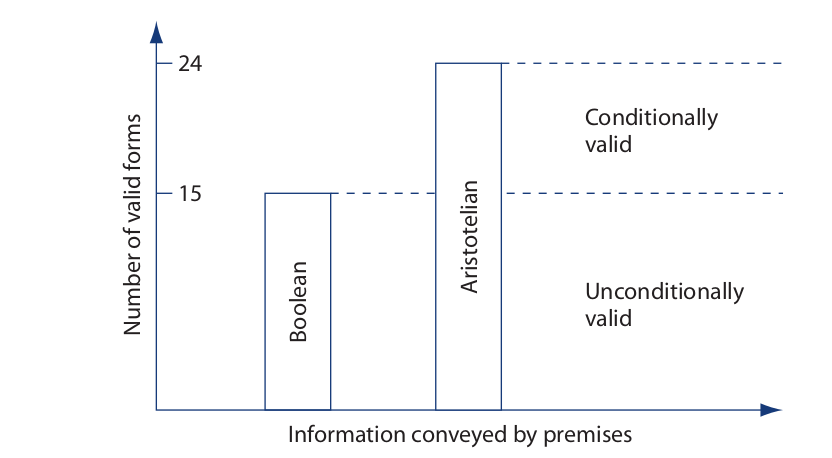
The graph shows that when the premises of a syllogistic form are recognized as conveying information about existence, an additional nine forms become valid.
5.2 Venn Diagrams
Because syllogisms contain three terms, whereas propositions contain only two, the application of Venn diagrams to syllogisms requires three overlapping circles.
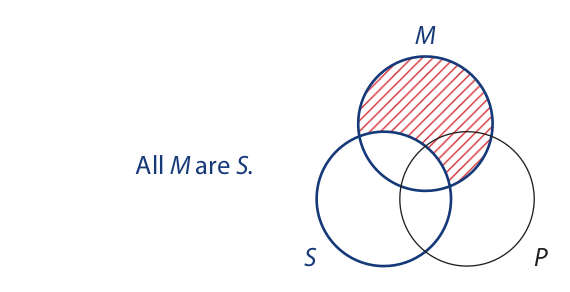
These circles should be drawn so that seven areas are clearly distinguishable within the diagram. The second step is to label the circles, one for each term. The precise order of the labeling is not critical, but we will adopt the convention of always assigning the lower-left circle to the subject of the conclusion, the lower-right circle to the predicate of the conclusion, and the top circle to the middle term. This convention is easy to remember because it conforms to the arrangement of the terms in a standardform syllogism: The subject of the conclusion is on the lower left, the predicate of the conclusion is on the lower right, and the middle term is in the premises, above the conclusion.
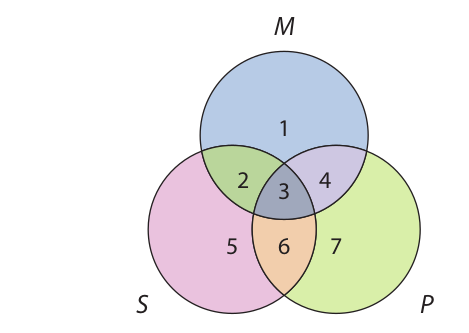
Anything in the area marked “1” is an M but neither an S nor a P, anything in the area marked “2” is both an S and an M but not a P, anything in the area marked “3” is a member of all three classes, and so on.
The test procedure consists of transferring the information content of the premises to the diagram and then inspecting the diagram to see whether it necessarily implies the truth of the conclusion. If the information in the diagram does do this, the argument is valid; otherwise it is invalid.
The use of Venn diagrams to evaluate syllogisms usually requires a little practice at first. Perhaps the best way of learning the technique is through illustrative examples, but a few pointers are needed first:
1. Marks (shading or placing an X) are entered only for the premises. No marks are made for the conclusion.
2. If the argument contains one universal premise, this premise should be entered first in the diagram. If there are two universal premises, either one can be done first.
3. When entering the information contained in a premise, one should concentrate on the circles corresponding to the two terms in the statement. While the third circle cannot be ignored altogether, it should be given only minimal attention.
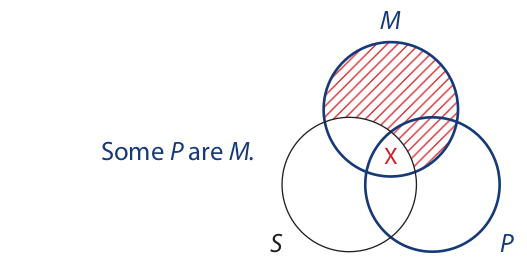
4. When inspecting a completed diagram to see whether it supports a particular conclusion, one should remember that particular statements assert two things. “Some S are P” means “At least one S exists and that S is a P”; “Some S are not P” means “At least one S exists and that S is not a P.”
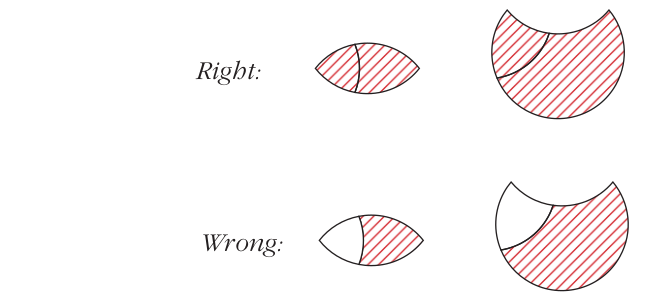
5. When shading an area, one must be careful to shade all of the area in question. Examples:
6. The area where an X goes is always initially divided into two parts. If one of these parts has already been shaded, the X goes in the unshaded part. Examples:
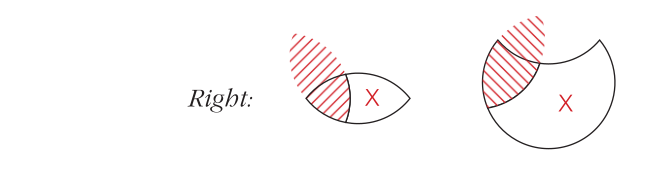
If one of the two parts is not shaded, the X goes on the line separating the two parts. Examples:
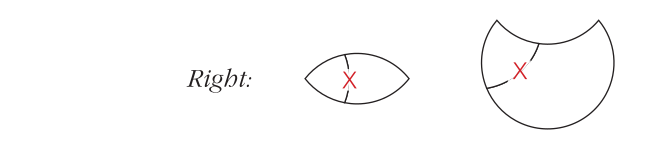
This means that the X may be in either (or both) of the two areas—but it is not known which one.
7. An X should never be placed in such a way that it dangles outside of the diagram, and it should never be placed on the intersection of two lines.
Boolean Standpoint
Because the Boolean standpoint does not recognize universal premises as having existential import, its approach to testing syllogisms is simpler and more general than that of the Aristotelian standpoint. Hence, we will begin by testing syllogisms from that standpoint and later proceed to the Aristotelian standpoint. Here is an example:
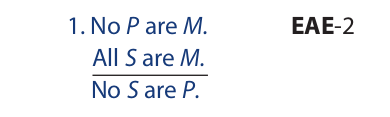
Since both premises are universal, it makes no difference which premise we enter first in the diagram. To enter the major premise, we concentrate our attention on the M and P circles, which are highlighted with color:
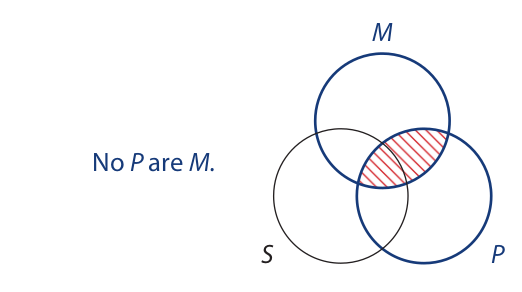
We now complete the diagram by entering the minor premise. In doing so, we concentrate our attention on the S and M circles, which are highlighted with color:
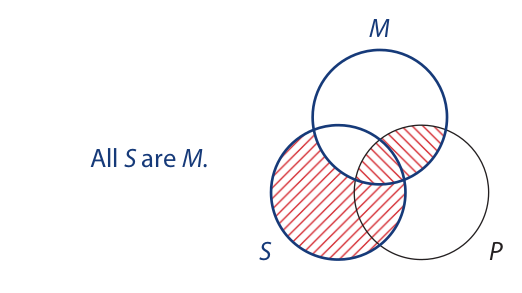
The conclusion states that the area where the S and P circles overlap is shaded. Inspection of the diagram reveals that this area is indeed shaded, so the syllogistic form is valid. Because the form is valid from the Boolean standpoint, it is unconditionally valid. In other words, it is valid regardless of whether its premises are recognized as having existential import.
Here is another example:
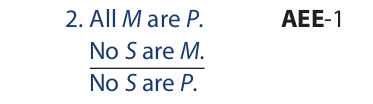
Again, both premises are universal, so it makes no difference which premise we enter first in the diagram. To enter the major premise, we concentrate our attention on the M and P circles:
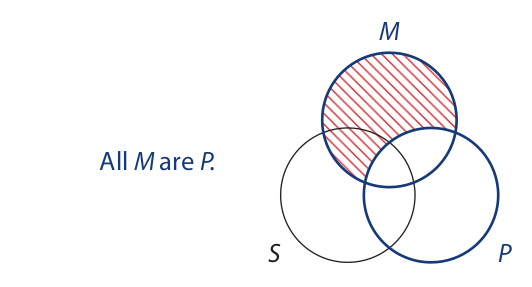
To enter the minor premise, we concentrate our attention on the M and S circles:
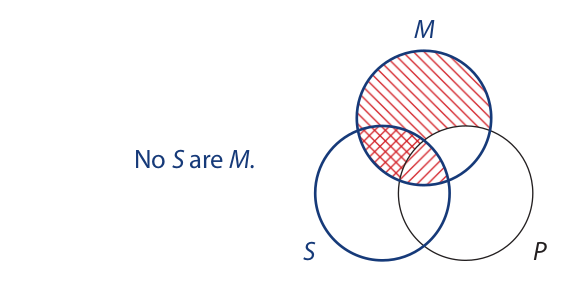
Again, the conclusion states that the area where the S and P circles overlap is shaded. Inspection of the diagram reveals that only part of this area is shaded, so the syllogistic form is invalid.
Another example:

We enter the universal premise first. To do so, we concentrate our attention on the M and S circles:
To enter the particular premise, we concentrate our attention on the M and P circles. This premise tells us to place an X in the area where the M and P circles overlap. Because part of this area is shaded, we place the X in the remaining area:
The conclusion states that there is an X in the area where the S and P circles overlap. Inspection of the diagram reveals that there is indeed an X in this area, so the syllogistic form is valid.
The examples that follow are done in a single step.

The universal premise is entered first. The particular premise tells us to place an X in the part of the S circle that lies outside the M circle. Because part of this area is shaded, we place the X in the remaining area. The conclusion states that there is an X that is inside the S circle but outside the P circle. Inspection of the diagram reveals that there is indeed an X in this area, so the syllogistic form is valid.
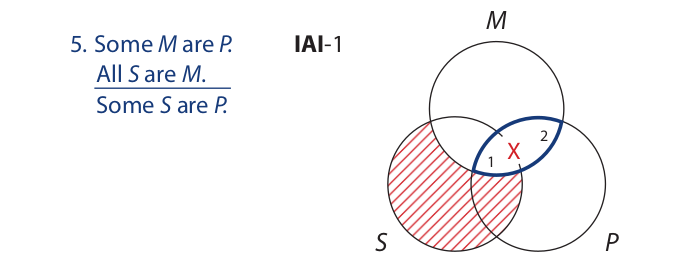
As usual, we enter the universal premise first. In entering the particular premise, we concentrate on the area where the M and P circles overlap. (For emphasis, this area is colored in the diagram.) Because this overlap area is divided into two parts (the areas marked “1” and “2”), we place the X on the line (arc of the S circle) that separates the two parts. The conclusion states that there is an X in the area where the S and P circles overlap. Inspection of the diagram reveals that the single X is dangling outside of this overlap area. We do not know if it is in or out. Thus, the syllogistic form is invalid.
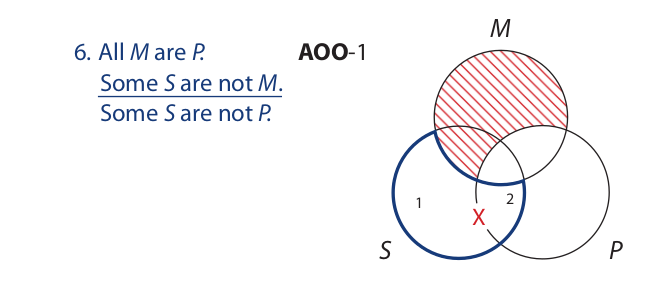
In entering the particular premise, we concentrate our attention on the part of the S circle that lies outside the M circle (colored area). Because this area is divided into two parts (the areas marked “1” and “2”), we place the X on the line (arc of the P circle) separating the two areas. The conclusion states that there is an X that is inside the S circle but outside the P circle. There is an X in the S circle, but we do not know whether it is inside or outside the P circle. Hence, the syllogistic form is invalid.
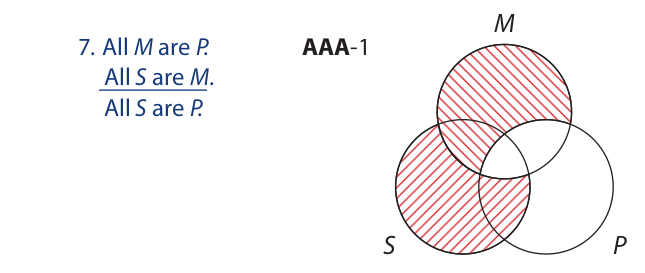
This is the “Barbara” syllogism. The conclusion states that the part of the S circle that is outside the P circle is empty. Inspection of the diagram reveals that this area is indeed empty. Thus, the syllogistic form is valid.
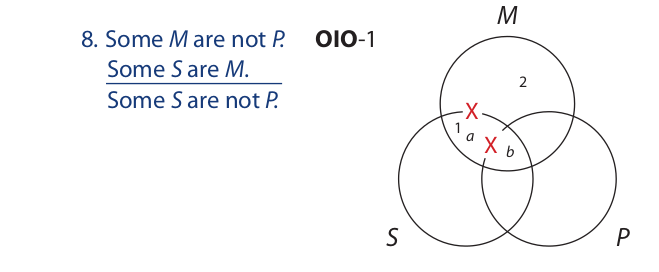
In this diagram no areas have been shaded, so there are two possible areas for each of the two X’s. The X from the first premise goes on the line (arc of the S circle) separating areas 1 and 2, and the X from the second premise goes on the line (arc of the P circle) separating areas a and b. The conclusion states that there is an X that is inside the S circle but outside the P circle. We have no certainty that the X from the first premise is inside the S circle, and while the X from the second premise is inside the S circle, we have no certainty that it is outside the P circle. Hence, the syllogistic form is invalid.
We have yet to explain the rationale for placing the X on the boundary separating two areas when neither of the areas is shaded. Consider this syllogistic form:
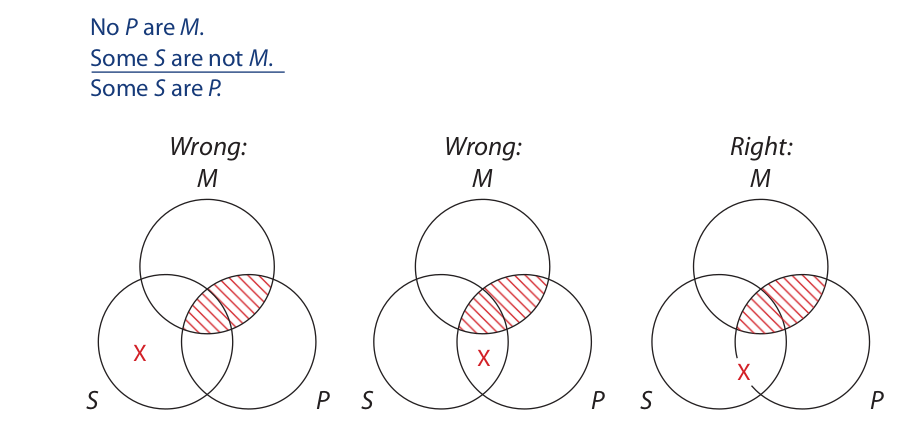
In each of the three diagrams the content of the first premise is represented correctly. The problem concerns placing the X from the second premise. In the first diagram the X is placed inside the S circle but outside both the M circle and the P circle. This diagram asserts: “At least one S is not an M and it is also not a P.” Clearly the diagram says more than the premise does, and so it is incorrect. In the second diagram the X is placed inside the S circle, outside the M circle, and inside the P circle. This diagram asserts: “At least one S is not an M, but it is a P.” Again, the diagram says more than the premise says, and so it is incorrect. In the third diagram, which is done correctly, the X is placed on the boundary between the two areas. This diagram asserts: “At least one S is not an M, and it may or may not be a P.” In other words, nothing at all is said about P, and so the diagram represents exactly the content of the second premise.
Aristotelian Standpoint
For the syllogistic forms tested thus far, we have adopted the Boolean standpoint, which does not recognize universal premises as having existential import. We now shift to the Aristotelian standpoint, where existential import can make a difference to validity. To test a syllogism from the Aristotelian standpoint, we follow basically the same procedure we followed in Section 4.6 to test immediate inferences:
1. Reduce the syllogism to its form and test it from the Boolean standpoint. If the form is valid, proceed no further. The syllogism is valid from both standpoints.
2. If the syllogistic form is invalid from the Boolean standpoint and has universal premises and a particular conclusion, then adopt the Aristotelian standpoint and look to see if there is a Venn circle that is completely shaded except for one area. If there is, enter a circled X in that area and retest the form.
3. If the syllogistic form is conditionally valid, determine if the circled X represents something that exists. If it does, the condition is fulfilled, and the syllogism is valid from the Aristotelian standpoint.
In regard to step 2, if the diagram contains no Venn circle completely shaded except for one area, then the syllogism is invalid from the Aristotelian standpoint. However, if it does contain such a Venn circle and the syllogism has a particular conclusion, then we place a circled X in the one unshaded area. This circled X represents the temporary assumption that the Venn circle in question is not empty.
In regard to step 3, if the circled X does not represent something that exists, then the syllogism is invalid. As we will see in Section 5.3, such syllogisms commit the existential fallacy from the Aristotelian standpoint.
The table of conditionally valid syllogistic forms presented in Section 5.1 names nine forms that are valid from the Aristotelian standpoint if a certain condition is fulfilled. The following syllogism has one of those forms:

First, we replace the terms with letters and test the syllogism from the Boolean standpoint:

The conclusion asserts that there is an X that is inside the C circle but outside the T circle. Inspection of the diagram reveals no X’s at all, so the syllogism is invalid from the Boolean standpoint. Proceeding to step 2, we adopt the Aristotelian standpoint and, noting that the conclusion is particular and that the F circle is all shaded except for one area, we enter a circled X in that area:
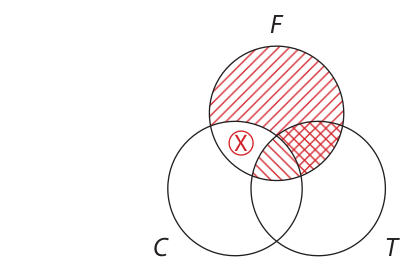
The diagram now indicates that the syllogism is conditionally valid, so we proceed to step 3 and determine whether the circled X represents something that actually exists. Since the circled X represents an F, and since F stands for fighter pilots, the circled X does represent something that exists. Thus, the condition is fulfilled, and the syllogism is valid from the Aristotelian standpoint.
Here is another example:

First we test the syllogism from the Boolean standpoint:
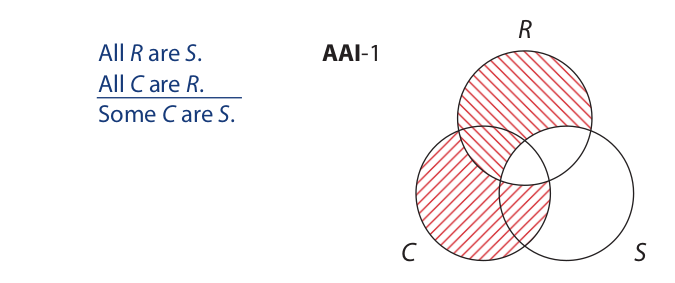
The conclusion asserts that there is an X in the area where the C and S circles overlap. Since the diagram contains no X’s at all, the syllogism is invalid from the Boolean standpoint. Proceeding to step 2, we adopt the Aristotelian standpoint. Then, after noticing that the conclusion is particular and that the C circle is all shaded except for one area, we enter a circled X in that area:
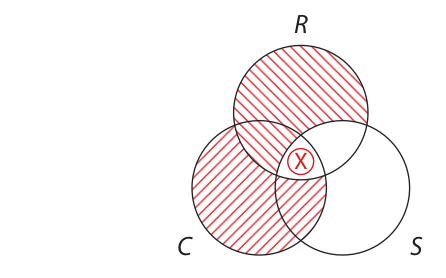
The diagram now indicates that the syllogism is conditionally valid, so we proceed to the third step and determine whether the circled X represents something that actually exists. Since the circled X represents a C, and C stands for currently living tyrannosaurs, the circled X does not represent something that actually exists. Thus, the condition is not fulfilled, and the syllogism is invalid. As we will see in the next section of this chapter, the syllogism commits the existential fallacy from the Aristotelian standpoint.
In determining whether the circled X stands for something that exists, we always look to the Venn circle that is all shaded except for one area. If the term corresponding to that circle denotes existing things, then the circled X represents one of those things. In some diagrams, however, there may be two Venn circles that are all shaded except for one area, and each may contain a circled X in the unshaded area. In these cases we direct our attention only to the circled X needed to draw the conclusion. If that circled X stands for something that exists, the argument is valid; if not, it is invalid.
5.3 Rules and Fallacies
The idea that valid syllogisms conform to certain rules was first expressed by Aristotle. Many such rules are discussed in Aristotle’s own account, but logicians of today generally settle on five or six.* If any one of these rules is violated, a specific formal fallacy is committed and, accordingly, the syllogism is invalid. Conversely, if none of the rules is broken, the syllogism is valid. These rules may be used as a convenient cross-check against the method of Venn diagrams. We will first consider the rules as they apply from the Boolean standpoint, and then shift to the Aristotelian standpoint.
Boolean Standpoint
Of the five rules presented in this section, the first two depend on the concept of distribution, the second two on the concept of quality, and the last on the concept of quantity.


In this standard-form categorical syllogism the middle term is “fish.” In both premises “fish” occurs as the predicate of an A proposition and therefore it is not distributed in either premise. Thus, the syllogism commits the fallacy of undistributed middle and is invalid. If the major premise were rewritten to read “All fish are sharks,” then “fish” would be distributed in that premise and the syllogism would be valid. But, of course, it would still be unsound because the rewritten premise would be false.
The logic behind Rule 1 may be explained by recounting how the middle term accomplishes its intended purpose, which is to provide a common ground between the subject and predicate terms of the conclusion. Let us designate the minor, major, and middle terms by the letters S, P, and M, respectively, and let us suppose that M is distributed in the major premise. By definition, P is related to the whole of the M class. Then, when the M class is related either in whole or in part to S, S and P necessarily become related. Analogous reasoning prevails if we suppose that M is distributed in the minor premise. But if M is undistributed in both premises, S and P may be related to different parts of the M class, in which case there is no common ground for relating S and P. This is exactly what happens in our fish example. The terms “salmon” and “sharks” are related to different parts of the fish class, so no common ground exists for relating them.

In the first example the major term, “animals,” is distributed in the conclusion but not in the major premise, so the syllogism commits the fallacy of illicit major, or, more precisely, “illicit process of the major term.” In the second example the minor term, “animals,” is distributed in the conclusion but not in the minor premise. The second example therefore commits the fallacy of illicit minor, or “illicit process of the minor term.”
In applying this rule, one must always examine the conclusion first. If no terms are distributed in the conclusion, Rule 2 cannot be violated. If one or both terms in the conclusion are distributed, then the appropriate premise must be examined. If the term distributed in the conclusion is also distributed in the premise, then the rule is not violated. But, if the term is not distributed in the premise, the rule is violated and the syllogism is invalid. In applying Rule 2 (and also Rule 1), you may find it helpful to begin by marking all the distributed terms in the syllogism—either by circling them or by labeling them with a small letter “d.”
The logic behind Rule 2 is easy to understand. Let us once again designate the minor, major, and middle terms by the letters S, P, and M, respectively, and let us suppose that a certain syllogism commits the fallacy of illicit major. The conclusion of that syllogism then makes an assertion about every member of the P class, but the major premise makes an assertion about only some members of the P class. Because the minor premise, by itself, says nothing at all about the P class, the conclusion clearly contains information not contained in the premises, and the syllogism is therefore invalid. Analogous reasoning applies to the fallacy of illicit minor.
Rule 2 becomes intuitively plausible when it is recognized that distribution is a positive attribute. Granting this, an argument that has a term distributed in the conclusion but not in the premises has more in the conclusion than it does in the premises and is therefore invalid. Of course, it is always permissible to have more in a premise than appears in the conclusion, so it is perfectly all right for a term to be distributed in a premise but not in the conclusion.

This syllogism may be seen as invalid because it has true premises and a false conclusion. The defect stems from the fact that it has two negative premises.
On reflection, Rule 3 should be fairly obvious. Let S, P, and M once again designate the minor, major, and middle terms. Now, if the P class and the M class are separate either wholly or partially, and the S class and the M class are separate either wholly or partially, nothing is said about the relation between the S class and the P class. These two classes may be either distinct or identical in whole or in part. Venn diagrams may be used effectively to illustrate the fact that no conclusion can be validly drawn from two negative premises.

These arguments may be seen as invalid because each has true premises and a false conclusion. The first draws an affirmative conclusion from a negative premise, and the second draws a negative conclusion from affirmative premises.
The logic behind Rule 4 may be seen as follows. If S, P, and M once again designate the minor, major, and middle terms, an affirmative conclusion always states that the S class is contained either wholly or partially in the P class. The only way that such a conclusion can follow is if the S class is contained either wholly or partially in the M class, and the M class wholly in the P class. In other words, it follows only when both premises are affirmative. But if, for example, the S class is contained either wholly or partially in the M class, and the M class is separate either wholly or partially from the P class, such a conclusion will never follow. Thus, an affirmative conclusion cannot be drawn from negative premises.
Conversely, a negative conclusion asserts that the S class is separate either wholly or partially from the P class. But if both premises are affirmative, they assert class inclusion rather than separation. Thus, a negative conclusion cannot be drawn from affirmative premises.
As a result of the interaction of these first four rules, it turns out that no valid syllogism can have two particular premises. This result is convenient to keep in mind, because it allows us to identify as invalid any standard-form syllogism in which both premises start with “some.” Because it is logically derivable from the first four rules, a separate rule to this effect is not given here.

The example has two universal premises and a particular conclusion, so it violates Rule 5. It commits the existential fallacy from the Boolean standpoint. The reason the syllogism is invalid from the Boolean standpoint is that the conclusion asserts that tigers exist, whereas the premises make no such assertion. From the Boolean standpoint, universal premises have no existential import.
In applying Rule 5, keep in mind that the existential fallacy is a fallacy that occurs when a syllogism is invalid merely because the premises lack existential import. Thus, if a syllogism is invalid for some other reason (that is, if it commits some other fallacy), it does not commit the existential fallacy. Hence, before deciding that a syllogism breaks Rule 5, make certain that no other rule is violated. If a syllogism does break one of the other four rules, Rule 5 does not apply.
Aristotelian Standpoint
Any categorical syllogism that breaks one of the first four rules is invalid from the Aristotelian standpoint. However, if a syllogism breaks only Rule 5, it is valid from the Aristotelian standpoint on condition that the critical term denotes at least one existing thing. (The critical term is the term listed in the farthest right-hand column of the table of conditionally valid syllogistic forms presented in Section 5.1.) In the example given in connection with Rule 5, the critical term is “tigers,” and the syllogism breaks no other rules, so it is valid from the Aristotelian standpoint. The conclusion asserts that tigers exist, and from the Aristotelian standpoint the premises imply their existence. On the other hand, consider the following example:

In this example, the critical term is “unicorns.” Since unicorns do not exist, the premises have no existential import from the Aristotelian standpoint. Thus, the syllogism is invalid from the Aristotelian standpoint, and it commits the existential fallacy from that standpoint. Of course, it also commits the existential fallacy from the Boolean standpoint.
In addition to consulting the table of conditionally valid forms, one way of identifying the critical term is to draw a Venn diagram. The critical term is the one that corresponds to the circle that is all shaded except for one area. In the case of two such circles, it is the one that corresponds to the Venn circle containing the circled X on which the conclusion depends. Another way of identifying the critical term is through examination of the distributed terms in the syllogism. The critical term is the one that is superfluously distributed. In other words, it is the term that, in the premises, is distributed in more occurrences than is necessary for the syllogism to obey all the rules. Here are three examples:
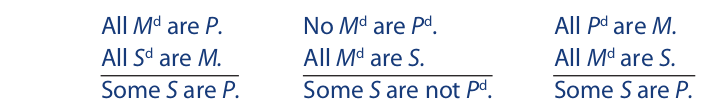
The distributed terms are tagged with a small “d.” In the first syllogism, M must be distributed to satisfy Rule 1, but S, in the second premise, need not be distributed to satisfy any rule. Thus, by the superfluous distribution rule, S is the term that must denote actually existing things for the syllogism to be valid from the Aristotelian standpoint. In the second syllogism, P must be distributed in the first premise to satisfy Rule 2, and M must be distributed once to satisfy Rule 1; but M is distributed twice. Thus, M is the term that must denote existing things for the syllogism to be valid from the Aristotelian standpoint. In the third syllogism, M must be distributed to satisfy Rule 1, but P need not be distributed to satisfy any rule. Thus, in this syllogism, P is the critical term.
5.4 Reducing the Number of Terms
In this section we consider arguments that contain more than three terms but that can be modified to reduce the number of terms to three. Consider the following:

This syllogism is clearly not in standard form because it has six terms: “photographers,” “editors,” “writers,” “non-photographers,” “non-editors,” and “non-writers.” But because three of the terms are complements of the other three, the number of terms can be reduced to a total of three, each used twice in distinct propositions. To accomplish the reduction, we can use the three operations of conversion, obversion, and contraposition discussed in Chapter 4. But, of course, since the reworked syllogism must be equivalent in meaning to the original one, we must use these operations only on the kinds of statements for which they yield logically equivalent results. That is, we must use conversion only on E and I statements and contraposition only on A and O statements. Obversion yields logically equivalent results for all four kinds of categorical statements.
Let us rewrite our six-term argument using letters to represent the terms, and then obvert the first premise and contrapose the conclusion in order to eliminate the negated letters:

Because the first premise of the original argument is an A statement and the conclusion an O statement, and because the operations performed on these statements yield logically equivalent results, the reduced argument is equivalent in meaning to the original argument. The reduced argument is in standard syllogistic form and may be evaluated either with a Venn diagram or by the five rules for syllogisms. The application of these methods indicates that the reduced argument is valid. We conclude, therefore, that the original argument is also valid.
It is not necessary to eliminate the negated terms in order to reduce the number of terms. It is equally effective to convert certain nonnegated terms into negated ones. Thus, instead of obverting the first premise of the example argument and contraposing the conclusion, we could have contraposed the first premise and converted and then obverted the second premise. The operation is performed as follows:

The reduced argument is once again equivalent to the original one, but now we must reverse the order of the premises to put the syllogism into standard form:

When tested with a Venn diagram or by means of the five rules, this argument will, of course, also be found valid, and so the original argument is valid. When using a Venn diagram, no unusual method is needed; the diagram is simply lettered with the three terms “W,” “non-E,” and “non-P.”
The most important point to remember in reducing the number of terms is that conversion and contraposition must never be used on statements for which they yield undetermined results. That is, conversion must never be used on A and O statements, and contraposition must never be used on E and I statements. The operations that are allowed are summarized as follows:

5.5 Ordinary Language Arguments
Many arguments that are not standard-form categorical syllogisms as written can be translated into standard-form syllogisms. In doing so we often use techniques developed in the last section of Chapter 4—namely, inserting quantifiers, modifying subject and predicate terms, and introducing copulas. The goal, of course, is to produce an argument consisting of three standard-form categorical propositions that contain a total of three different terms, each of which occurs twice in distinct propositions. Once translated, the argument can be tested by means of a Venn diagram or the rules for syllogisms.
Since the task of translating arguments into standard-form syllogisms involves not only converting the component statements into standard form but adjusting these statements one to another so that their terms occur in matched pairs, a certain amount of practice may be required before it can be done with facility. In reducing the terms to three matched pairs it is often helpful to identify some factor common to two or all three propositions and to express this common factor through the strategic use of parameters. For example, if all three statements are about people, the term “people” or “people identical to” might be used; or if they are about times or places, the term “times” or “times identical to” or the term “places” or “places identical to” might be used. Here is an example:

The temporal adverbs “whenever” and “today” suggest that “times” should be used as the common factor. Following this suggestion, we have this:

This is a standard-form categorical syllogism. Notice that each of the three terms is matched with an exact duplicate in a different proposition. To obtain such a match, it is sometimes necessary to alter the wording of the original statement just slightly. Now if we adopt the convention
M = times people put off marriage until they are older
D = times the divorce rate decreases
P = present times
the syllogism may be symbolized as follows:

Here is another example:

For this argument the parameter “companies” suggests itself:

The first statement, of course, is the conclusion. When the syllogism is written in standard form, it will be seen that it has, like the previous syllogism, the form AAA-1.
Here is another example:

To translate this argument, using a single common factor is not necessary:

This syllogism commits the fallacy of illicit major and is therefore invalid.
As was mentioned in Section 4.7, arguments containing an exceptive proposition must be handled in a special way. Let us consider one that contains an exceptive proposition as a premise:

The first premise is translated as two conjoined categorical propositions: “No Levi’s are jeans on sale,” and “All jeans that are not Levi’s are jeans on sale.” These give rise to two syllogisms:

The first syllogism, which is in standard form, is invalid because it has two negative premises. The second one, on the other hand, is not in standard form, because it has four terms. If the second premise is obverted, so that it reads “All Calvin Klein jeans are jeans that are not Levi’s,” the syllogism becomes an AAA-1 standard-form syllogism, which is valid.
Each of these two syllogisms may be viewed as a pathway in which the conclusion of the original argument might follow necessarily from the premises. Since it does follow via the second syllogism, the original argument is valid. If both of the resulting syllogisms turned out to be invalid, the original argument would be invalid.
5.6 Enthymemes
An enthymeme is an argument that is expressible as a categorical syllogism but that is missing a premise or a conclusion. Examples:

The first enthymeme is missing the premise “Whatever encourages waste and high prices should be abolished,” and the second is missing the conclusion “Lost pets should not be sold to a medical laboratory.”
Enthymemes occur frequently in ordinary spoken and written English for several reasons. Sometimes it is simply boring to express every statement in an argument. The listener or reader’s intelligence is called into play when he or she is required to supply a missing statement, thereby sustaining his or her interest. On other occasions the arguer may want to slip an invalid or unsound argument past an unwary listener or reader, and this aim may be facilitated by leaving a premise or conclusion out of the picture.
Many enthymemes are easy to convert into syllogisms. The reader or listener must first determine what is missing, whether premise or conclusion, and then introduce the missing statement with the aim of converting the enthymeme into a good argument. Attention to indicator words will often provide the clue as to the nature of the missing statement, but a little practice can render this task virtually automatic. The missing statement need not be expressed in categorical form; expressing it in the general context of the other statements is sufficient and is often the easier alternative. Once this is done, the entire argument may be translated into categorical form and then tested with a Venn diagram or by the rules for syllogisms. Example:

Translating this argument into categorical form, we have

This syllogism is valid (and sound).
Any enthymeme (such as the one about Venus) that contains an indicator word is missing a premise. This may be seen as follows. If an enthymeme contains a conclusion indicator, then the conclusion follows it, which means that the missing statement is a premise. On the other hand, if the enthymeme contains a premise indicator, then the conclusion precedes it, which means, again, that the missing statement is a premise.
If, however, an enthymeme contains no indicator words at all (such as the two enthymemes at the beginning of this section), then the missing statement could be either a premise or a conclusion. If the two given statements are joined by a word such as “and,” “but,” “moreover,” or some similar conjunction, the missing statement is usually a conclusion. If not, the first statement is usually the conclusion, and the missing statement is a premise. To test this latter alternative, it may help to mentally insert the word “because” between the two statements. If this insertion makes sense, the missing statement is a premise.
After the nature of the missing statement has been determined, the next task is to write it out. To do so, one must first identify its terms. This can be done by taking account of the terms that are given. Two of the terms in the given statements will match up with each other. Once this pair of terms is found, attention should be focused on the other two terms. These are the ones that will be used to form the missing statement. In constructing the missing statement, attention to the rules for syllogisms may be helpful (if the resulting syllogism is to be valid). For example, if the missing statement is a conclusion and one of the given premises is negative, the missing conclusion must be negative. Or if the missing statement is a premise and the stated conclusion is universal, the missing premise must be universal.
The enthymemes that we have considered thus far have been fairly straightforward. The kinds of enthymemes that occur in letters to the editor of magazines and newspapers often require a bit more creativity to convert into syllogisms. Consider the following:

The conclusion is the last statement, and the missing premise is that any vehicle that has served as basic transportation for the poor for decades deserves to be celebrated. The enthymeme may be written as a standard-form syllogism as follows:

The syllogism is valid and arguably sound. Here is another example:

In this argument the author draws three connections: the connection between doctors’ smoking and doctors’ caring about their own health, between doctors’ caring about their own health and doctors’ caring about the author’s health, and between doctors’ caring about the author’s health and doctors who will have the author as a patient. Two arguments are needed to express these connections:

And,

Notice that the conclusion of the first argument becomes a premise in the second argument. To put these arguments into final standard form the order of the premises must be reversed. Both arguments are valid, but probably not sound.
5.7 Sorites
A sorites is a chain of categorical syllogisms in which the intermediate conclusions have been left out. The name is derived from the Greek word soros, meaning “heap,” and is pronounced “sōrītëz,” with the accent on the second syllable. The plural form is also “sorites.” Here is an example:

The first two premises validly imply the intermediate conclusion “All bloodhounds are mammals.” If this intermediate conclusion is then treated as a premise and put together with the third premise, the final conclusion follows validly. The sorites is thus composed of two valid categorical syllogisms and is therefore valid. The rule in evaluating a sorites is based on the idea that a chain is only as strong as its weakest link. If any of the component syllogisms in a sorites is invalid, the entire sorites is invalid.
A standard-form sorites is one in which each of the component propositions is in standard form, each term occurs twice, the predicate of the conclusion is in the first premise, and each successive premise has a term in common with the preceding one.* The sorites in the example is in standard form. Each of the propositions is in standard form, each term occurs twice; the predicate of the conclusion, “bloodhounds,” is in the first premise; the other term is in the first premise; “dogs,” is in the second premise, and so on.
We will now introduce two techniques for testing a sorites for validity. The first technique involves three steps: (1) put the sorites into standard form, (2) introduce the intermediate conclusions, and (3) test each component syllogism for validity. If each component is valid, the sorites is valid. Consider the following sorites form:

To put the sorites form into standard form, the premises must be rearranged. To do this find the premise that contains the predicate of the conclusion and write it first. Then find the premise that contains the other term in the first premise and write it second. Continue in this way until all the premises are listed:

Next, the intermediate conclusions are drawn. Venn diagrams are useful in performing this step, and they serve simultaneously to check the validity of each component syllogism:
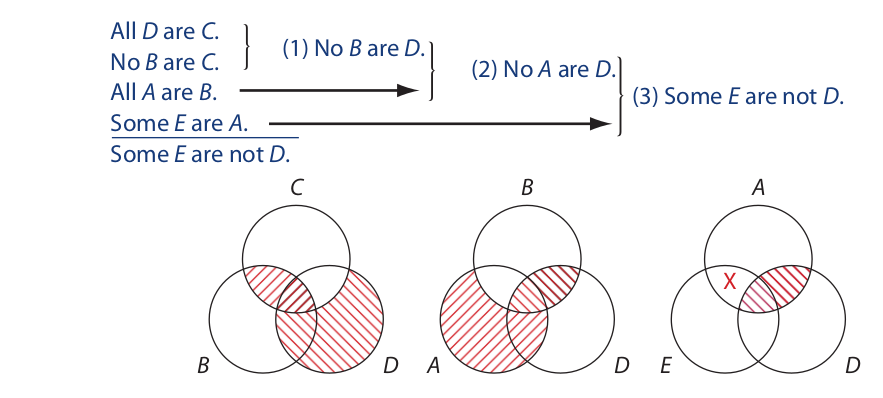
The first intermediate conclusion, “No B are D,” is drawn from the first two premises. The second, “No A are D,” is drawn from the first intermediate conclusion and the third premise. And the third conclusion, which is identical to the final conclusion, is drawn from the second intermediate conclusion and the fourth premise. Since all conclusions are drawn validly, the sorites is valid. On the other hand, if at some step in the procedure no conclusion can be drawn, the sorites is invalid.
The second technique for testing the validity of a sorites is faster and simpler than the first one because it does not require that the intermediate conclusions be derived.
This second technique consists in applying five rules that closely resemble the rules for syllogisms. The rules are as follows:

Rule 1 refers to the “middle terms” in the sorites. These are the terms that occur in matched pairs in the premises. The conclusion referred to in Rules 2, 4, and 5 is the final conclusion of the sorites. Also, as with categorical syllogisms, if a sorites breaks only Rule 5, it is valid from the Aristotelian standpoint on condition that its terms refer to existing things.
Before applying the rules, it helps to put the sorites into standard form; in either event the sorites must be written so that the terms occur in matched pairs. The following sorites is in standard form, and the distributed terms are marked with a small “d.” As is apparent, there are three middle terms: M, K, and R.

This sorites breaks Rule 1 because neither occurrence of M in the first two premises is distributed. Thus, the sorites is invalid. Note that no other rule is broken. Both of the K’s in lines 2 and 3 are distributed, one of the R’s in lines 3 and 4 is distributed, S is distributed in the conclusion and also in the first premise, there is a negative conclusion and only one negative premise, and while the conclusion is particular so is one of the premises. The logic behind the five rules is as follows.
For Rule 1, each of the middle terms in the sorites is also a middle term in one of the component syllogisms. Thus, if Rule 1 is broken, one of the component syllogisms has an undistributed middle, making the entire sorites invalid.
For Rule 2, when the sorites is in standard form, the predicate of the conclusion must appear in each of the intermediate conclusions. Thus, if the predicate of the conclusion is distributed, it must also be distributed in each of the intermediate conclusions, and also in the first premise. Otherwise, one of the component syllogisms would have either an illicit major or an illicit minor, making the entire sorites invalid. Analogously, if the subject of the conclusion is distributed, it must also be distributed in the last premise. Otherwise, the last component syllogism would have an illicit minor, making the entire sorites invalid.
For Rule 3, when a negative premise appears in the list of premises, the conclusion derived from that premise must be negative, as must all subsequent conclusions. Other wise, one of the component syllogisms would break Rule 4 for syllogisms. If a second negative premise should appear, the syllogism consisting of that premise and the prior intermediate conclusion would commit the fallacy of exclusive premises, making the entire sorites invalid.
Similarly, for Rule 4, when a negative premise appears in the list of premises, all subsequent conclusions must be negative. Otherwise, one of the component syllogisms would break Rule 4 for syllogisms. Conversely, if the conclusion of the sorites is negative, either the last premise or the last intermediate conclusion must be negative. Otherwise, the last component syllogism would break Rule 4 for syllogisms. If the last intermediate conclusion is negative, then either the prior premise or the prior intermediate conclusion must be negative. If we continue this reasoning, we see that some prior premise must be negative.
For Rule 5, a particular conclusion has existential import, while universal premises (from the Boolean standpoint) do not. Thus, if all the premises are universal and the conclusion is particular, the sorites as a whole commits the existential fallacy.
One of the advantages of the rules method for testing a sorites is that invalidity can often be detected through immediate inspection. Once a sorites has been put into standard form, any sorites having more than one negative premise is invalid, and any sorites having a negative premise and an affirmative conclusion (or vice versa) is invalid. Also, as with syllogisms, any sorites having more than one particular premise is invalid. This last requirement is implied by the other rules.




 浙公网安备 33010602011771号
浙公网安备 33010602011771号