A Concise Introduction to Logic - PART II: FORMAL LOGIC - Chapter 4: Categorical Propositions

PART II: FORMAL LOGIC

Chapter 4: Categorical Propositions

4.1 The Components of Categorical Propositions

A proposition that relates two classes, or categories, is called a categorical proposition. The classes in question are denoted respectively by the subject term and the predicate term, and the proposition asserts that either all or part of the class denoted by the subject term is included in or excluded from the class denoted by the predicate term. Here are some examples of categorical propositions:

The first statement asserts that the entire class of American Idol contestants is included in the class of people who hope for recognition, the second that the entire class of junk foods is excluded from the class of things that belong in school caffeterias, and the third that part of the class of today’s unemployed people is included in the class of people who have given up on finding work. The fourth statement asserts that part of the class of romances is excluded from the class of things that have a happy ending, and the last statement asserts that the class that has Oprah Winfrey as its single member is included in the class of people who publish magazines.

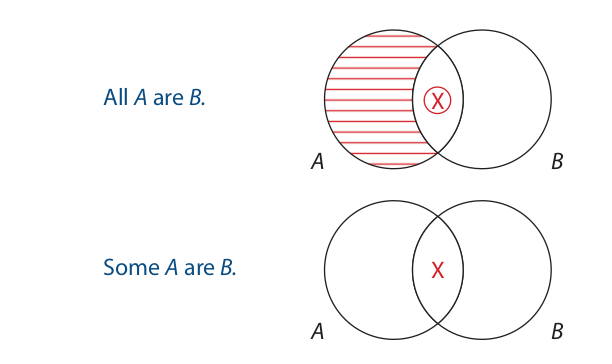
Since any categorical proposition asserts that either all or part of the class denoted by the subject term is included in or excluded from the class denoted by the predicate term, it follows that there are exactly four types of categorical propositions: (1) those that assert that the whole subject class is included in the predicate class, (2) those that assert that part of the subject class is included in the predicate class, (3) those that assert that the whole subject class is excluded from the predicate class, and (4) those that assert that part of the subject class is excluded from the predicate class. A categorical proposition that expresses these relations with complete clarity is called a standard-form categorical proposition. A categorical proposition is in standard form if and only if it is a substitution instance of one of the following four forms:

All S are P.
No S are P.
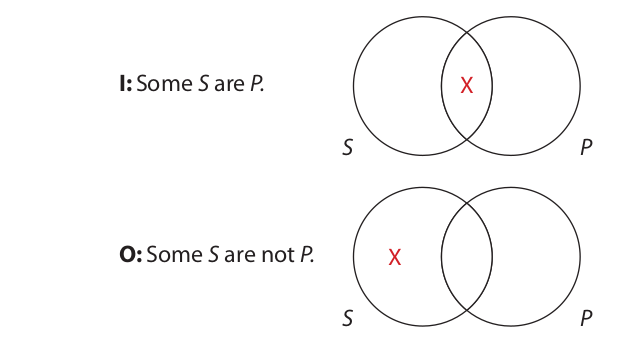
Some S are P.
Some S are not P.

Many categorical propositions, of course, are not in standard form because, among other things, they do not begin with the words “all,” “no,” or “some.”

The words “all,” “no,” and “some” are called quantifiers because they specify how much of the subject class is included in or excluded from the predicate class.

The letters S and P stand respectively for the subject and predicate terms, and the words “are” and “are not” are called the copula because they link (or “couple”) the subject term with the predicate term.

 

4.2 Quality, Quantity, and Distribution

The quality of a categorical proposition is either affirmative or negative depending on whether it affirms or denies class membership. Accordingly, “All S are P” and “Some S are P” have affirmative quality, and “No S are P” and “Some S are not P” have negative quality. These are called affirmative propositions and negative propositions, respectively.

 

The quantity of a categorical proposition is either universal or particular, depending on whether the statement makes a claim about every member or just some member of the class denoted by the subject term. “All S are P” and “No S are P” each assert something about every member of the S class and thus are universal propositions. “Some S are P” and “Some S are not P” assert something about one or more members of the S class and hence are particular propositions.

 

Note that the quantity of a categorical proposition may be determined through mere inspection of the quantifier. “All” and “no” immediately imply universal quantity, while “some” implies particular. But categorical propositions have no “qualifier.” In universal propositions the quality is determined by the quantifier, and in particular propositions it is determined by the copula.

 

Particular propositions mean no more and no less than the meaning assigned to them in class notation. The statement “Some S are P” does not imply that some S are not P, and the statement “Some S are not P” does not imply that some S are P. It often happens, of course, that substitution instances of these statement forms are both true.

 

Since the early Middle Ages the four kinds of categorical propositions have commonly been designated by letter names corresponding to the first four vowels of the Roman alphabet: A, E, I, O. The universal affirmative is called an A proposition, the universal negative an E proposition, the particular affirmative an I proposition, and the particular negative an O proposition.

 

The material presented thus far in this section may be summarized as follows:

Unlike quality and quantity, which are attributes of propositions, distribution is an attribute of the terms (subject and predicate) of propositions. A term is said to be distributed if the proposition makes an assertion about every member of the class denoted by the term; otherwise, it is undistributed. Stated another way, a term is distributed if and only if the statement assigns (or distributes) an attribute to every member of the class denoted by the term. Thus, if a statement asserts something about every member of the S class, then S is distributed; if it asserts something about every member of the P class, then P is distributed; otherwise S and P are undistributed.

Let us imagine that the members of the classes denoted by the subject and predicate terms of a categorical proposition are contained respectively in circles marked with the letters “S” and “P.” The meaning of the statement form “All S are P” may then be represented by the following diagram:

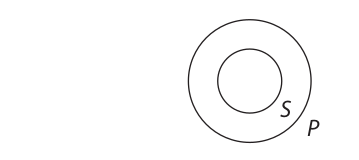
The S circle is contained in the P circle, which represents the fact that every member of S is a member of P. (Of course, should S and P represent terms denoting identical classes, the two circles would overlap exactly.) As the diagram shows, “All S are P” makes a claim about every member of the S class, since the statement says that every member of S is in the P class. But the statement does not make a claim about every member of the P class, since there may be some members of P that are outside of S. Thus, by the definition of “distributed term” given above, S is distributed and P is not. In other words, for any universal affirmative (A) proposition, the subject term, whatever it may be, is distributed, and the predicate term is undistributed.

Let us now consider the universal negative (E) proposition. “No S are P” states that the S and P classes are separate, which may be represented as follows:

This statement makes a claim about every member of S and every member of P. It asserts that every member of S is separate from every member of P, and also that every member of P is separate from every member of S. Accordingly, by our definition, both the subject and predicate terms of universal negative (E) propositions are distributed.

The particular affirmative (I) proposition states that at least one member of S is a member of P. If we represent this one member of S that we are certain about by an asterisk, the resulting diagram looks like this:

Since the asterisk is inside the P class, it represents something that is simultaneously an S and a P; in other words, it represents a member of the S class that is also a member of the P class. Thus, the statement “Some S are P” makes a claim about one member (at least) of S and also one member (at least) of P, but not about all members of either class. Hence, by the definition of distribution, neither S nor P is distributed.

The particular negative (O) proposition asserts that at least one member of S is not a member of P. If we once again represent this one member of S by an asterisk, the resulting diagram is as follows:

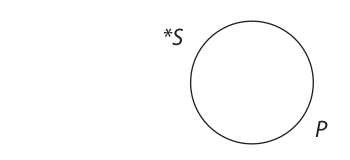
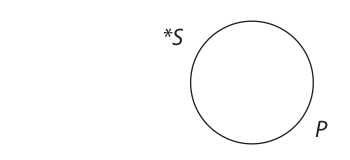
Since the other members of S may or may not be outside of P, it is clear that the statement “Some S are not P” does not make a claim about every member of S, so S is not distributed. But, as may be seen from the diagram, the statement does assert that every member of P is separate and distinct from this one member of S that is outside the P circle. Thus, in the particular negative (O) proposition, P is distributed and S is undistributed.

At this point the notion of distribution may be somewhat vague and elusive. Unfortunately, there is no simple and easy way to make the idea graphically clear. The best that can be done is to repeat some of the things that have already been said. First of all, distribution is an attribute or quality that the subject and predicate terms of a categorical proposition may or may not possess, depending on the kind of proposition. If the proposition in question is an A type, then the subject term, whatever it may be, is distributed. If it is an E type, then both terms are distributed; if an I type, then neither; and if an O type, then the predicate. If a certain term is distributed in a proposition, this simply means that the proposition says something about every member of the class that the term denotes. If a term is undistributed, the proposition does not say something about every member of the class.

 

4.3 Venn Diagrams and the Modern Square of Opposition

Existential Import

The primary goal of our inquiry into categorical propositions is to disclose the role that such propositions play in the formation of arguments. However, it turns out that we can interpret universal (A and E) propositions in two different ways, and according to one of these interpretations an argument might be valid, while according to the other it might be invalid. Thus, before turning to the evaluation of arguments, we must explore the two possible interpretations of universal propositions. Our investigation will focus on what is called existential import. To illustrate this concept, consider the following pair of propositions:

The first proposition implies that Tom Cruise has indeed made some movies. In other words, the statement has existential import. It implies that one or more things denoted by the subject term actually exist. On the other hand, no such implication is made by the statement about unicorns. The statement is true, because unicorns, by definition, have a single horn. But the statement does not imply that unicorns actually exist.

Thus, the question arises: Should universal propositions be interpreted as implying that the things talked about actually exist? Or should they be interpreted as implying no such thing? In response to this question, logicians have taken two different approaches. Aristotle held that universal propositions about existing things have existential import. In other words, such statements imply the existence of the things talked about:

Aristotelian standpoint

The first two statements have existential import because their subject terms denote actually existing things. The third statement has no existential import, because satyrs do not exist.

On the other hand, the nineteenth-century logician George Boole held that no universal propositions have existential import. Such statements never imply the existence of the things talked about:

Boolean standpoint

We might summarize these results by saying that the Aristotelian standpoint is “open” to existence.* When things exist, the Aristotelian standpoint recognizes their existence, and universal statements about those things have existential import. In other words, existence counts for something. On the other hand, the Boolean standpoint is “closed” to existence. When things exist, the Boolean standpoint does not recognize their existence, and universal statements about those things have no existential import.

The Aristotelian standpoint differs from the Boolean standpoint only with regard to universal (A and E) propositions. The two standpoints are identical with regard to particular (I and O) propositions. Both the Aristotelian and the Boolean standpoints recognize that particular propositions make a positive assertion about existence. For example, from both standpoints, the statement “Some cats are animals” asserts that at least one cat exists, and that cat is an animal. Also, from both standpoints, “Some fish are not mammals” asserts that at least one fish exists, and that fish is not a mammal. Thus, from both standpoints, the word “some” implies existence.

 

Venn Diagrams

From the Boolean standpoint, the four kinds of categorical propositions have the following meaning. Notice that the first two (universal) propositions imply nothing about the existence of the things denoted by S:

All S are P. = No members of S are outside P.
No S are P. = No members of S are inside P.
Some S are P. = At least one S exists, and that S is a P.
Some S are not P. = At least one S exists, and that S is not a P.

Adopting this interpretation of categorical propositions, the nineteenth-century logician John Venn developed a system of diagrams to represent the information they express. These diagrams have come to be known as Venn diagrams.

A Venn diagram is an arrangement of overlapping circles in which each circle represents the class denoted by a term in a categorical proposition. Because every categorical proposition has exactly two terms, the Venn diagram for a single categorical proposition consists of two overlapping circles. Each circle is labeled so that it represents one of the terms in the proposition. Unless otherwise required, we adopt the convention that the left-hand circle represents the subject term, and the right-hand circle the predicate term. Such a diagram looks like this:

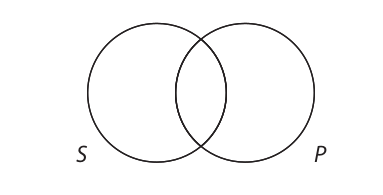
The members of the class denoted by each term should be thought of as situated inside the corresponding circle. Thus, the members of the S class (if any such members exist) are situated inside the S circle, and the members of the P class (if any such members exist) are situated inside the P circle. If any members are situated inside the area where the two circles overlap, then such members belong to both the S class and the P class. Finally, if any members are situated outside both circles, they are members of neither S nor P.

Suppose, for example, that the S class is the class of Americans and the P class is the class of farmers. Then, if we use numerals to identify the four possible areas, the diagram looks like this:

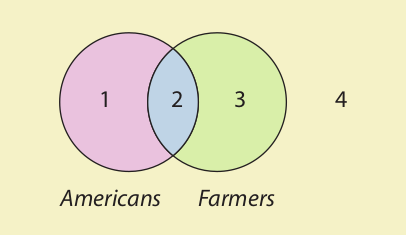
Anything in the area marked “1” is an American but not a farmer, anything in the area marked “2” is both an American and a farmer, and anything in the area marked “3” is a farmer but not an American. The area marked “4” is the area outside both circles; thus, anything in this area is neither a farmer nor an American.

We can now use Venn diagrams to represent the information expressed by the four kinds of categorical proposition. To do this we make a certain kind of mark in a diagram. Two kinds of marks are used: shading an area and placing an X in an area. Shading an area means that the shaded area is empty,* and placing an X in an area means that at least one thing exists in that area. The X may be thought of as representing that one thing. If no mark appears in an area, this means that nothing is known about that area; it may contain members or it may be empty. Shading is always used to represent the content of universal (A and E) propositions, and placing an X in an area is always used to represent the content of particular (I and O) propositions. The content of the four kinds of categorical propositions is represented as follows:

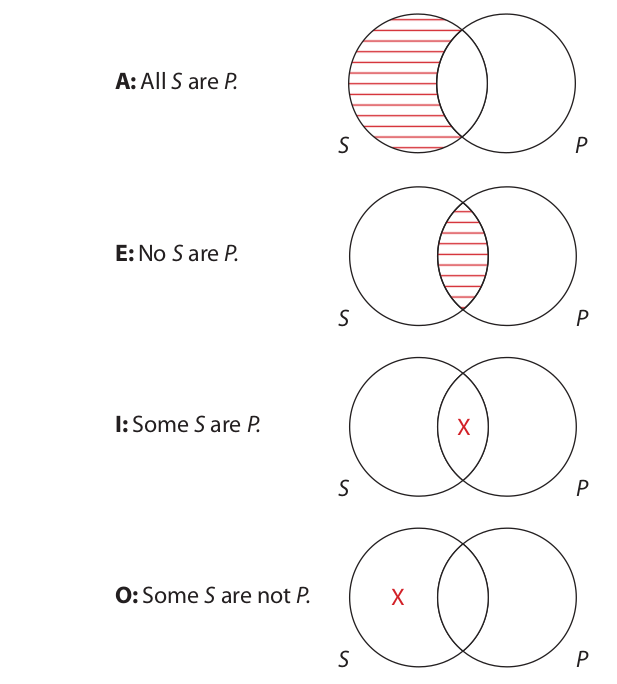
Recall that the A proposition asserts that no members of S are outside P. This is represented by shading the part of the S circle that lies outside the P circle. The E proposition asserts that no members of S are inside P. This is represented by shading the part of the S circle that lies inside the P circle. The I proposition asserts that at least one S exists and that S is also a P. This is represented by placing an X in the area where the S and P circles overlap. This X represents an existing thing that is both an S and a P. Finally, the O proposition asserts that at least one S exists, and that S is not a P. This is represented by placing an X in the part of the S circle that lies outside the P circle. This X represents an existing thing that is an S but not a P.

Because there is no X in the diagrams that represent the universal propositions, these diagrams say nothing about existence. For example, the diagram for the A proposition merely asserts that nothing exists in the part of the S circle that lies outside the P circle. The area where the two circles overlap and the part of the P circle that lies outside the S circle contain no marks at all. This means that something might exist in these areas, or they might be completely empty. Similarly, in the diagram for the E proposition, no marks appear in the left-hand part of the S circle and the right-hand part of the P circle. This means that these two areas might contain something or, on the other hand, they might not.

 

The Modern Square of Opposition

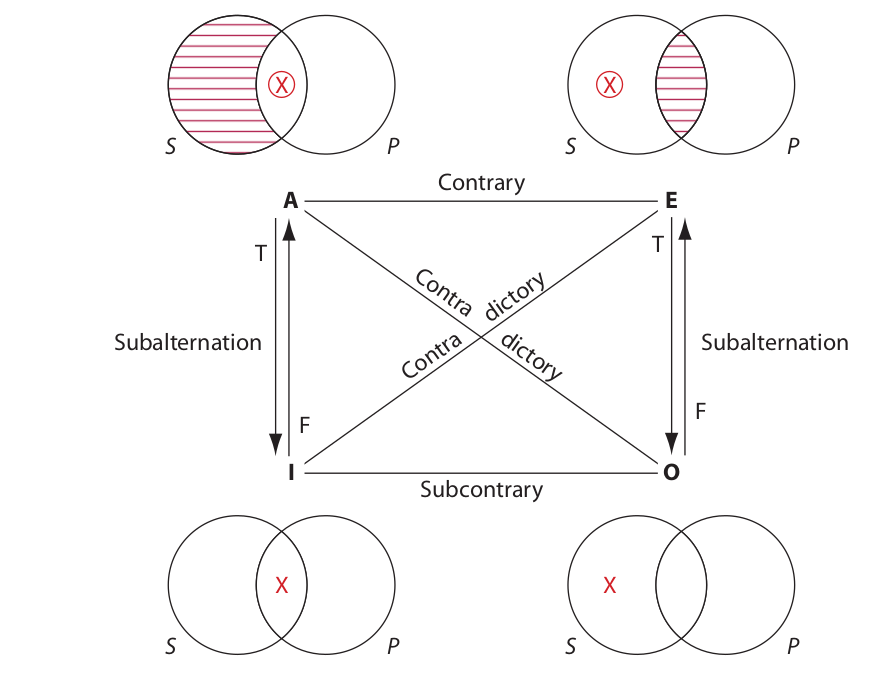
Let us compare the diagram for the A proposition with the diagram for the O proposition. The diagram for the A proposition asserts that the left-hand part of the S circle is empty, whereas the diagram for the O proposition asserts that this same area is not empty. These two diagrams make assertions that are the exact opposite of each other. As a result, their corresponding statements are said to contradict each other. Analogously, the diagram for the E proposition asserts that the area where the two circles overlap is empty, whereas the diagram for the I proposition asserts that the area where the two circles overlap is not empty. Accordingly, their corresponding propositions are also said to contradict each other. This relationship of mutually contradictory pairs of propositions is represented in a diagram called the modern square of opposition. This diagram, which arises from the modern (or Boolean) interpretation of categorical propositions, is represented as follows:

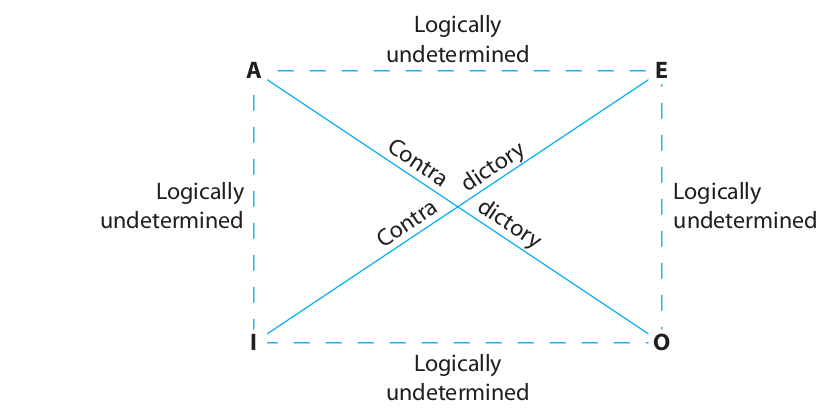
If two propositions are related by the contradictory relation, they necessarily have opposite truth value. Thus, if a certain A proposition is given as true, the corresponding O proposition must be false. Similarly, if a certain I proposition is given as false, the corresponding E proposition must be true. But no other inferences are possible. In particular, given the truth value of an A or O proposition, nothing can be determined about the truth value of the corresponding E or I propositions. These propositions are said to have logically undetermined truth value. Like all propositions, they do have a truth value, but logic alone cannot determine what it is. Similarly, given the truth value of an E or I proposition, nothing can be determined about the truth value of the corresponding A or O propositions. They, too, are said to have logically undetermined truth value.

 

Testing Immediate Inferences

Since the modern square of opposition provides logically necessary results, we can use it to test certain arguments for validity. We begin by assuming the premise is true, and we enter the pertinent truth value in the square. We then use the square to compute the truth value of the conclusion. If the square indicates that the conclusion is true, the argument is valid; if not, the argument is invalid. Here is an example:

Arguments of this sort are called immediate inferences because they have only one premise. Instead of reasoning from one premise to the next, and then to the conclusion, we proceed immediately to the conclusion. To test this argument for validity, we begin by assuming that the premise, which is an O proposition, is true, and we enter this truth value in the square of opposition. We then use the square to compute the truth value of the corresponding A proposition. By the contradictory relation, the A proposition is false. Since the conclusion claims that the A proposition is false, the conclusion is true, and therefore the argument is valid. Arguments that are valid from the Boolean standpoint are said to be unconditionally valid because they are valid regardless of whether their terms refer to existing things.

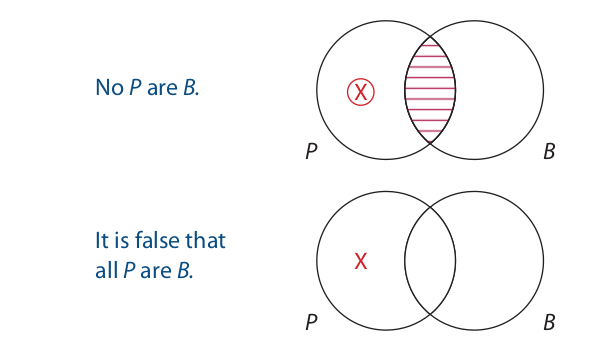
Note that the conclusion of this argument has the form “It is false that all S are P.” Technically, statements of this type are not standard-form propositions because, among other things, they do not begin with a quantifier. To remedy this difficulty we adopt the convention that statements having this form are equivalent to “‘All S are P’ is false.” Analogous remarks apply to the negations of the E, I, and O statements.

We can also use Venn diagrams to test immediate inferences for validity. However, using this technique often requires that we diagram statements beginning with the phrase “It is false that.” Let us begin by showing how to diagram such statements. Here are two examples:

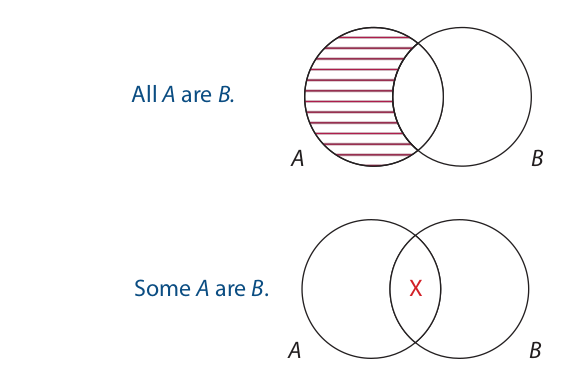
The first statement claims that “All A are B” is false. Thus, to diagram it, we do the　exact opposite of what we would do to diagram “All A are B.” To diagram “All A are　B,” we shade the left-hand part of the A circle:

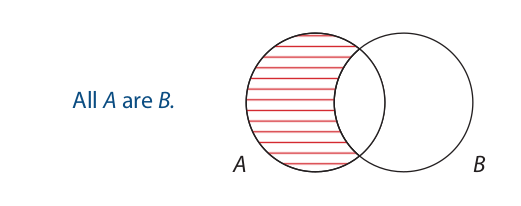
To diagram “It is false that all A are B,” we enter an X in the left-hand part of the　A circle. Entering an X in an area is the opposite of shading an area:

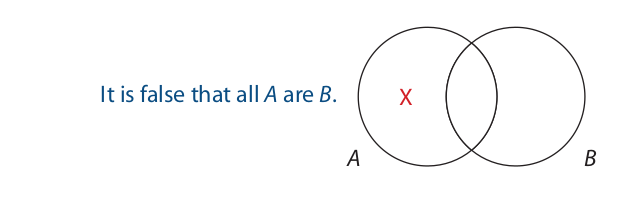
Any statement that is diagrammed by entering an X in an area is a particular proposition. Thus, as the diagram shows, “It is false that all A are B” is actually a particular proposition. By similar reasoning, “It is false that no A are B” is also a particular proposition.

To diagram “It is false that some A are B,” we do the exact opposite of what we would do to diagram “Some A are B.” For “Some A are B,” we would enter an X in the overlap area. Thus, to diagram “It is false that some A are B,” we shade the overlap area:

Any statement that is diagrammed by shading an area is a universal proposition. Thus, “It is false that some A are B” is actually a universal proposition. By similar reasoning, “It is false that some A are not B” is also a universal proposition.

Now let us use Venn diagrams to test an immediate inference. To do so we begin by using letters to represent the terms, and we then draw Venn diagrams for the premise and conclusion. If the information expressed by the conclusion diagram is contained in the premise diagram, the argument is valid; if not, it is invalid. Here is the symbolized form of the trade spies inference that we tested earlier.

The next step is to draw two Venn diagrams, one for the premise and the other for the conclusion. For the premise we enter an X in the left-hand part of the T circle, and for the conclusion, as we have just seen, we enter an X in the left-hand part of the T circle:

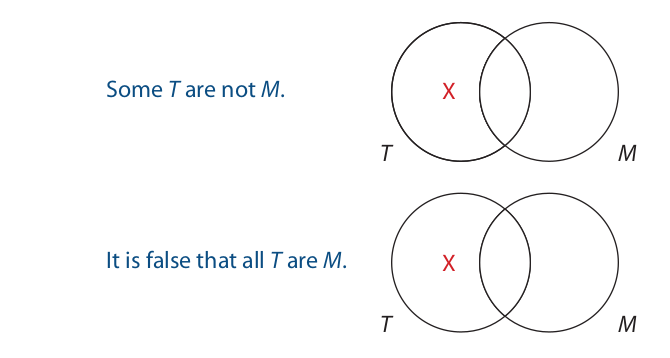
To evaluate the inference, we look to see whether the information expressed by the conclusion diagram is also expressed by the premise diagram. The conclusion diagram asserts that something exists in the left-hand part of the T circle. Since this information is also expressed by the premise diagram, the inference is valid. In this case, the diagram for the conclusion is identical to the diagram for the premise, so it is clear that premise and conclusion assert exactly the same thing. However, as we will see in Sections 4.5 and 4.6, for an immediate inference to be valid, it is not necessary that premise and conclusion assert exactly the same thing. It is only necessary that the premise assert at least as much as the conclusion.

Here is the symbolized version of the second inference evaluated earlier:

To diagram the premise, we enter an X in the left-hand part of the M circle, and for the conclusion we shade the overlap area:

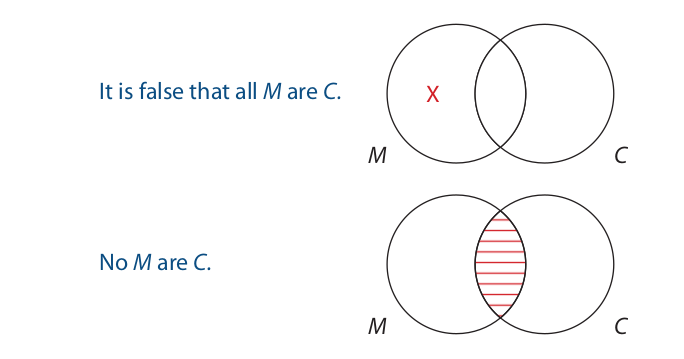
Here, the conclusion diagram asserts that the overlap area is empty. Since this information is not contained in the premise diagram, the inference is invalid.

We conclude with a special kind of inference:

The completed Venn diagrams are as follows:

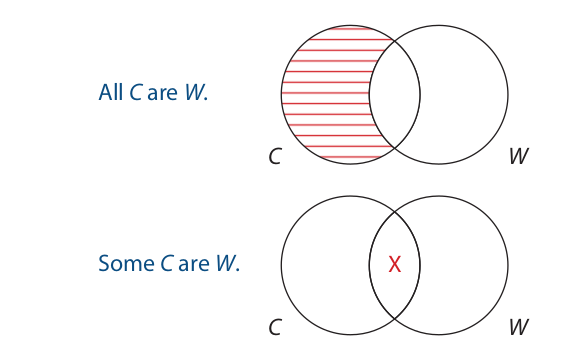
The information of the conclusion diagram is not contained in the premise diagram, so the inference is invalid. However, if the premise were interpreted as having existential import, then the C circle in the premise diagram would not be empty. Specifically, there would be members in the overlap area. This would make the inference valid.

Arguments of this sort are said to commit the existential fallacy. From the Boolean standpoint, the existential fallacy is a formal fallacy that occurs whenever an argument is invalid merely because the premise lacks existential import. Such arguments always have a universal premise and a particular conclusion. The fallacy consists in attempting to derive a conclusion having existential import from a premise that lacks it.

The existential fallacy is easy to detect. Just look for a pair of diagrams in which the premise diagram contains shading and the conclusion diagram contains an X. If the X in the conclusion diagram is in the same part of the left-hand circle that is unshaded in the premise diagram, then the inference commits the existential fallacy. In the example we just considered, the premise diagram contains shading, and the conclusion diagram contains an X. Also, the X in the conclusion diagram is in the overlap area, and this area is unshaded in the premise diagram. Thus, the inference commits the existential fallacy.

There are exactly eight inference forms that commit the existential fallacy. Four of them are as follows. (The other four are left for an exercise.) Among these forms, recall that any proposition asserting that a particular (I or O) proposition is false is a universal proposition, and any proposition asserting that a universal (A or E) proposition is false is a particular proposition. With this in mind, you can see that all of these forms proceed from a universal premise to a particular conclusion.

Existential fallacy

Finally, while all of these forms proceed from a universal premise to a particular conclusion, it is important to see that not every inference having a universal premise and a particular conclusion commits the existential fallacy. For example, the inference “All A are B; therefore, some A are not B” does not commit this fallacy. This inference is invalid because the conclusion contradicts the premise. Thus, to detect the existential fallacy, one must ensure that the invalidity results merely from the fact that the premise lacks existential import. This can easily be done by constructing a Venn diagram.

 

4.4 Conversion, Obversion, and Contraposition

Conversion

The simplest of the three operations is conversion, and it consists in switching the subject term with the predicate term. For example, if the statement “No foxes are hedgehogs” is converted, the resulting statement is “No hedgehogs are foxes.” This new statement is called the converse of the given statement. To see how the four types of categorical propositions relate to their converse, compare the following sets of Venn diagrams:

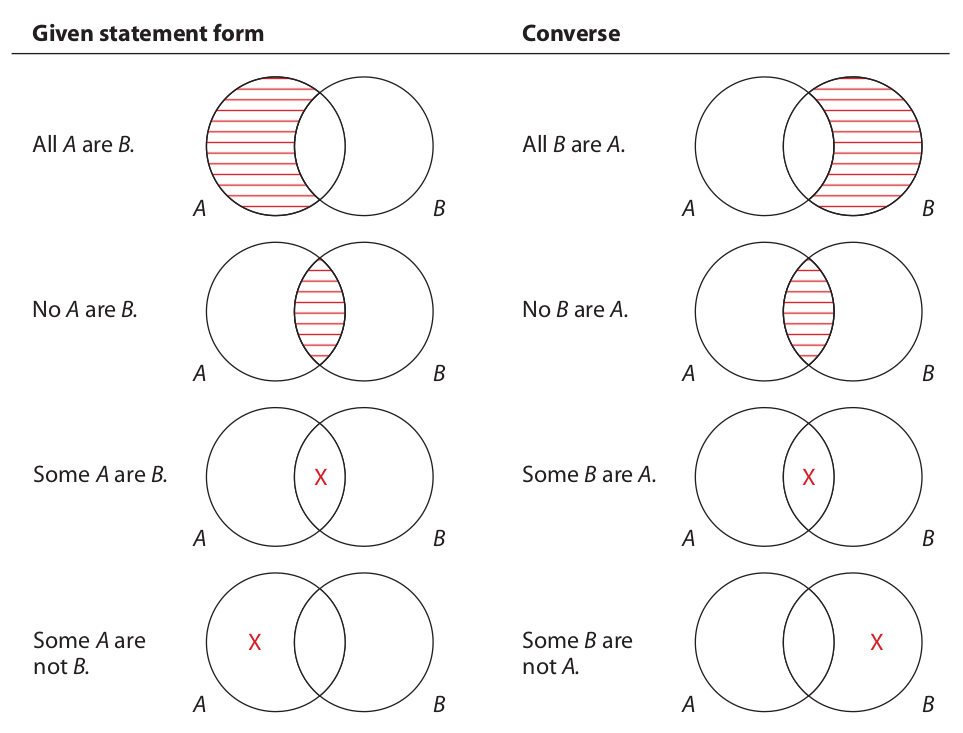
If we examine the diagram for the E statement, we see that it is identical to that of its converse. Also, the diagram for the I statement is identical to that of its converse. This means that the E statement and its converse are logically equivalent, and the I statement and its converse are logically equivalent. Two statements are said to be logically equivalent statements when they necessarily have the same truth value. Thus, converting an E or I statement gives a new statement that always has the same truth value (and the same meaning) as the given statement. These equivalences are strictly proved by the Venn diagrams for the E and I statements.

On the other hand, the diagram for the A statement is clearly not identical to the diagram for its converse, and the diagram for the O statement is not identical to the diagram for its converse. Also, these pairs of diagrams are not the exact opposite of each other, as is the case with contradictory statements. This means that an A statement and its converse are logically unrelated as to truth value, and an O statement and its converse are logically unrelated as to truth value. In other words, converting an A or O statement gives a new statement whose truth value is logically undetermined in relation to the given statement. The converse of an A or O statement does have a truth value, of course, but logic alone cannot tell us what it is.

Because conversion yields necessarily determined results for E and I statements, it can be used as the basis for immediate inferences having these types of statements as premises. The following inference forms are valid:

Since the conclusion of each inference form necessarily has the same truth value as the premise, if the premise is assumed true, it follows necessarily that the conclusion is true. On the other hand, the next two inference forms are invalid. Each commits the fallacy of illicit conversion:

Here are two examples of inferences that commit the fallacy of illicit conversion:

 

Obversion

More complicated than conversion, obversion requires two steps: (1) changing the quality (without changing the quantity), and (2) replacing the predicate with its term complement. The first part of this operation was treated in Exercise 4.2. It consists in changing “No S are P” to “All S are P” and vice versa, and changing “Some S are P” to “Some S are not P” and vice versa.

The second step requires understanding the concept of class complement. The complement of a class is the group consisting of everything outside the class. For example, the complement of the class of dogs is the group that includes everything that is not a dog (cats, fish, trees, and so on). The term complement is the word or group of words that denotes the class complement. For terms consisting of a single word, the term complement is usually formed by simply attaching the prefix “non” to the term. Thus, the complement of the term “dog” is “non-dog,” the complement of the term “book” is “non-book,” and so on.

The relationship between a term and its complement can be illustrated by a Venn diagram. For example, if a single circle is allowed to represent the class of dogs, then everything outside the circle represents the class of non-dogs:

We now have everything we need to form the obverse of categorical propositions. First we change the quality (without changing the quantity), and then we replace the predicate term with its term complement. For example, if we are given the statement “All horses are animals,” then the obverse is “No horses are non-animals”; and if we are given the statement “Some trees are maples,” then the obverse is “Some trees are not non-maples.” To see how the four types of categorical propositions relate to their obverse, compare the following sets of Venn diagrams:

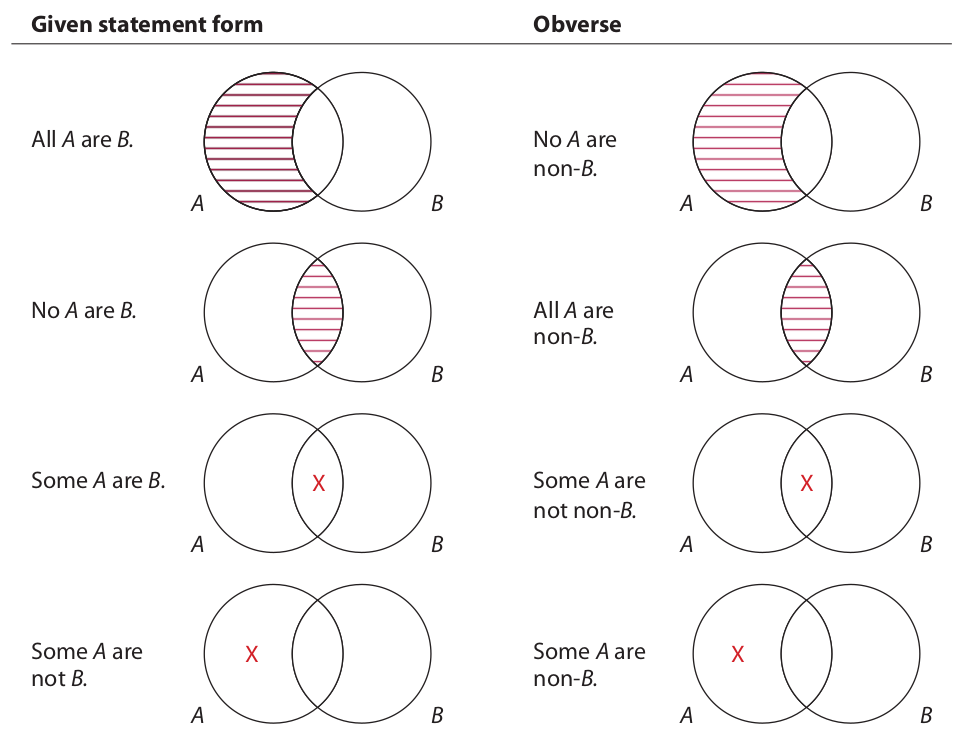
To see how the obverse diagrams are drawn, keep in mind that “non-B” designates the area outside the B circle. Thus, “No A are non-B” asserts that the area where A overlaps non-B is empty. This is represented by shading the left-hand part of the A circle. “All A are non-B” asserts that all members of A are outside B. This means that no members of A are inside B, so the area where A overlaps B is shaded. “Some A are not non-B” asserts that at least one member of A is not outside B. This means that at least one member of A is inside B, so an X is placed in the area where A and B overlap. Finally, “Some A are non-B” asserts that at least one member of A is outside B, so an X is placed in the left-hand part of the A circle.

If we examine these pairs of diagrams, we see that the diagram for each given statement form is identical to the diagram for its obverse. This means that each of the four types of categorical proposition is logically equivalent to (and has the same meaning as) its obverse. Thus, if we obvert an A statement that happens to be true, the resulting statement will be true; if we obvert an O statement that happens to be false, the resulting statement will be false, and so on.

It is easy to see that if a statement is obverted and then obverted again, the resulting statement will be identical to the original statement. For example, the obverse of “All horses are animals” is “No horses are non-animals.” To obvert the latter statement we again change the quality (“no” switches to “all”) and replace “non-animals” with its term complement. The term complement is produced by simply deleting the prefix “non.” Thus, the obverse of the obverse is “All horses are animals.”

When a term consists of more than a single word, more ingenuity is required to form its term complement. For example, if we are given the term “animals that are not native to America,” it would not be appropriate to form the term complement by writing “non-animals that are not native to America.” Clearly it would be better to write “animals native to America.” Even though this is technically not the complement of the given term, the procedure is justified if we allow a reduction in the scope of discourse. This can be seen as follows. Technically the term complement of “animals that are not native to America” denotes all kinds of things such as ripe tomatoes, battleships, gold rings, and so on. But if we suppose that we are talking only about animals (that is, we reduce the scope of discourse to animals), then the complement of this term is “animals native to America.”

As is the case with conversion, obversion can be used to supply the link between the premise and the conclusion of immediate inferences. The following inference forms are valid:

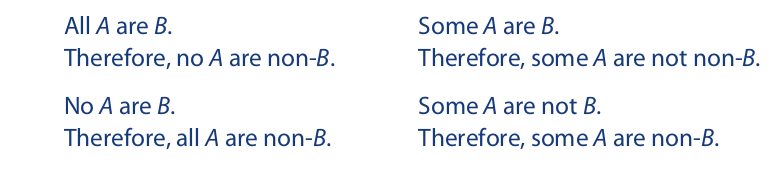
Because the conclusion of each inference form necessarily has the same truth value as its premise, if the premise is assumed true, it follows necessarily that the conclusion is true.

 

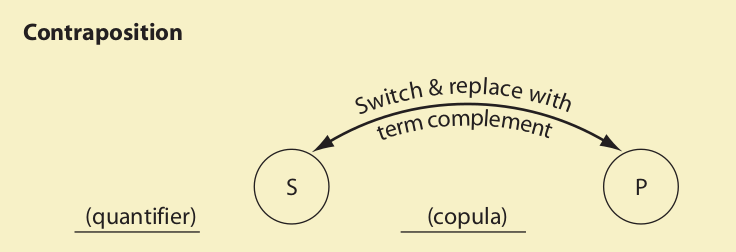
Contraposition

Like obversion, contraposition requires two steps: (1) switching the subject and predicate terms and (2) replacing the subject and predicate terms with their term complements. For example, if the statement “All goats are animals” is contraposed, the resulting statement is “All non-animals are non-goats.” This new statement is called the contrapositive of the given statement. To see how all four types of categorical propositions relate to their contrapositive, compare the following sets of diagrams:

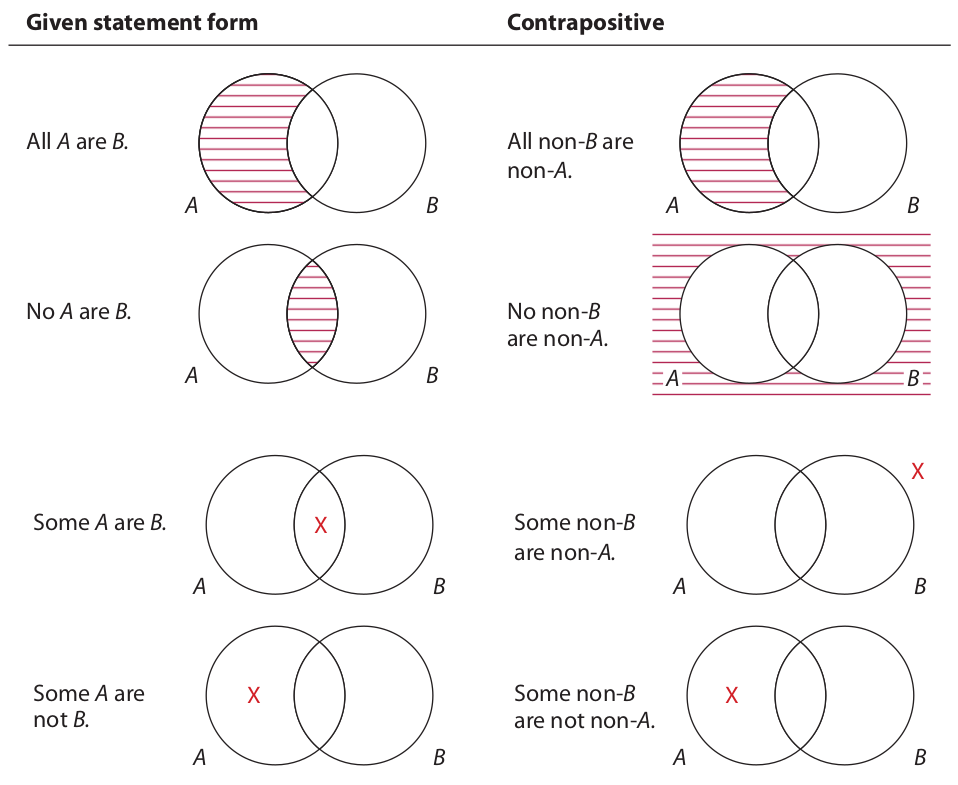
To see how the first diagram on the right is drawn, remember that “non-A” designates the area outside A. Thus, “All non-B are non-A” asserts that all members of non-B are outside A. This means that no members of non-B are inside A. Thus, we shade the area where non-B overlaps A. “No non-B are non-A” asserts that the area where non-B overlaps non-A is empty. Since non-B is the area outside the B circle and non-A is the area outside the A circle, the place where these two areas overlap is the area outside both circles. Thus, we shade this area. “Some non-B are non-A” asserts that something exists in the area where non-B overlaps non-A. Again, this is the area outside both circles, so we place an X in this area. Finally, “Some non-B are not non-A” asserts that at least one member of non-B is outside non-A. This means that at least one member of non-B is inside A, so we place an X in the area where non-B overlaps A.

Now, inspection of the diagrams for the A and O statements reveals that they are identical to the diagrams of their contrapositive. Thus, the A statement and its contrapositive are logically equivalent (and have the same meaning), and the O statement and its contrapositive are logically equivalent (and have the same meaning). On the other hand, the diagrams of the E and I statements are neither identical to nor the exact opposite of the diagrams of their contrapositives. This means that contraposing an E or I statement gives a new statement whose truth value is logically undetermined in relation to the given statement.

As with conversion and obversion, contraposition may provide the link between the premise and the conclusion of an immediate inference. The following inference forms are valid:

On the other hand, the following inference forms are invalid. Each commits the fallacy of illicit contraposition:

Here are two examples of inferences that commit the fallacy of illicit contraposition:

Both illicit conversion and illicit contraposition are formal fallacies: They can be detected through mere examination of the form of an argument.

Finally, note that the Boolean interpretation of categorical propositions has prevailed throughout this section. This means that the results obtained are unconditional, and they hold true regardless of whether the terms in the propositions denote actually existing things. Thus, they hold for propositions about unicorns and leprechauns just as they do for propositions about dogs and animals. These results are summarized in the following table.

 

4.5 The Traditional Square of Opposition

In Section 4.3 we adopted the Boolean standpoint, and we saw how the modern square of opposition applies regardless of whether the propositions refer to actually existing things. In this section, we adopt the Aristotelian standpoint, which recognizes that universal propositions about existing things have existential import. For such propositions the traditional square of opposition becomes applicable. Like the modern square, the traditional square of opposition is an arrangement of lines that illustrates logically necessary relations among the four kinds of categorical propositions. However, because the Aristotelian standpoint recognizes the additional factor of existential import, the traditional square supports more inferences than does the modern square. It is represented as follows:

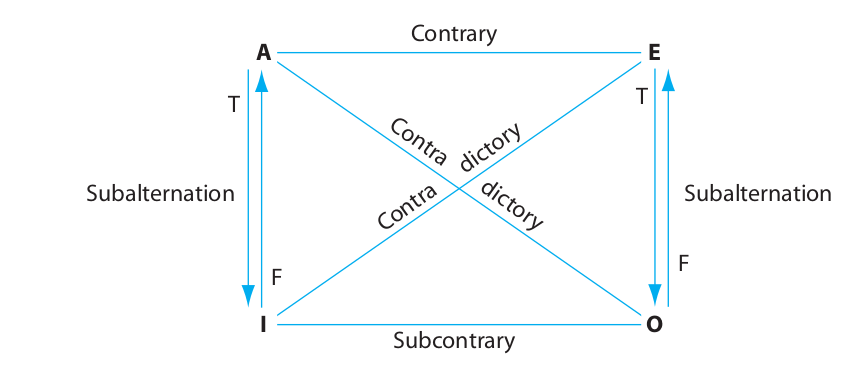
The four relations in the traditional square of opposition may be characterized as follows:

The contradictory relation is the same as that found in the modern square. Thus, if a certain A proposition is given as true, the corresponding O proposition is false, and vice versa, and if a certain A proposition is given as false, the corresponding O proposition is true, and vice versa. The same relation holds between the E and I propositions. The contradictory relation thus expresses complete opposition between propositions.

 

The contrary relation differs from the contradictory in that it expresses only partial opposition. Thus, if a certain A proposition is given as true, the corresponding E proposition is false (because at least one must be false), and if an E proposition is given as true, the corresponding A proposition is false. But if an A proposition is given as false, the corresponding E proposition could be either true or false without violating the “at least one is false” rule. In this case, the E proposition has logically undetermined truth value. Similarly, if an E proposition is given as false, the corresponding A proposition has logically undetermined truth value.

These results are borne out in ordinary language. Thus, if we are given the actually true A proposition “All cats are animals,” the corresponding E proposition “No cats are animals” is false, and if we are given the actually true E proposition “No cats are dogs,” the corresponding A proposition “All cats are dogs” is false. Thus, the A and E propositions cannot both be true. However, they can both be false. “All animals are cats” and “No animals are cats” are both false.

 

The subcontrary relation also expresses a kind of partial opposition. If a certain I proposition is given as false, the corresponding O proposition is true (because at least one must be true), and if an O proposition is given as false, the corresponding I proposition is true. But if either an I or an O proposition is given as true, then the corresponding proposition could be either true or false without violating the “at least one is true” rule. Thus, in this case the corresponding proposition would have logically undetermined truth value.

Again, these results are borne out in ordinary language. If we are given the actually false I proposition “Some cats are dogs,” the corresponding O proposition “Some cats are not dogs” is true, and if we are given the actually false O proposition “Some cats are not animals,” the corresponding I proposition “Some cats are animals” is true. Thus, the I and O propositions cannot both be false, but they can both be true. “Some animals are cats” and “Some animals are not cats” are both true.

 

The subalternation relation is represented by two arrows: a downward arrow marked with the letter T (true), and an upward arrow marked with an F (false). These arrows can be thought of as pipelines through which truth values “flow.” The downward arrow “transmits” only truth, and the upward arrow only falsity. Thus, if an A proposition is given as true, the corresponding I proposition is true also, and if an I proposition is given as false, the corresponding A proposition is false. But if an A proposition is given as false, this truth value cannot be transmitted downward, so the corresponding I proposition will have logically undetermined truth value. Conversely, if an I proposition is given as true, this truth value cannot be transmitted upward, so the corresponding A proposition will have logically undetermined truth value. Analogous reasoning prevails for the subalternation relation between the E and O propositions. To remember the direction of the arrows for subalternation, imagine that truth descends from “above,” and falsity rises up from “below.”

 

Testing Immediate Inferences

Next, let us see how we can use the traditional square of opposition to test immediate inferences for validity. Here is an example:

We begin, as usual, by assuming the premise is true. Since the premise is an A proposition, by the contrary relation the corresponding E proposition is false. But this is exactly what the conclusion says, so the argument is valid.

Here is another example:

Here the premise and conclusion are linked by the subcontrary relation. According to that relation, if the premise is assumed true, the conclusion has logically undetermined truth value, and so the inference is invalid. It commits the formal fallacy of illicit subcontrary. Analogously, inferences that depend on an incorrect application of the contrary relation commit the formal fallacy of illicit contrary, and inferences that depend on an illicit application of subalternation commit the formal fallacy of illicit subalternation. Some forms of these fallacies are as follows:

Cases of the incorrect application of the contradictory relation are so infrequent that an “illicit contradictory” fallacy is not usually recognized.

As we saw at the beginning of this section, for the traditional square of opposition to apply, the Aristotelian standpoint must be adopted, and the propositions to which it is applied must assert something about actually existing things. The question may now be asked, What happens when the Aristotelian standpoint is adopted but the propositions are about things that do not exist? The answer is that under these conditions the traditional square gives exactly the same results as the modern square (see Section 4.3). Inferences that are based on a correct application of the contradictory relation are valid, but inferences that are based on an otherwise correct application of the other three relations are invalid and commit the existential fallacy.

The reason for this result is easy to see. The modern square of opposition rests on the Boolean standpoint, and the traditional square rests on the Aristotelian standpoint. But the Aristotelian standpoint differs from the Boolean only with respect to universal propositions about existing things. The Aristotelian standpoint recognizes these propositions as having existential import, while the Boolean standpoint does not. But universal propositions about things that do not exist have no existential import from the Aristotelian standpoint. In other words, the Aristotelian standpoint interprets these propositions in exactly the same way as does the Boolean. Thus, for universal propositions about things that do not exist, the traditional square gives exactly the same results as the modern square.

Accordingly, the existential fallacy is committed from the Aristotelian standpoint when and only when contrary, subcontrary, and subalternation are used (in an otherwise correct way) to draw a conclusion from a premise about things that do not exist. All such inferences begin with a universal proposition, which has no existential import, and they conclude with a particular proposition, which has existential import. The existential fallacy is never committed in connection with the contradictory relation, nor is it committed in connection with conversion, obversion, or contraposition, all of which hold regardless of existence. The following inferences commit the existential fallacy from the Aristotelian standpoint:

The first depends on an otherwise correct use of the subalternation relation, and the second on an otherwise correct use of the contrary relation. If flying witches and magical wizards actually existed, both arguments would be valid. But since they do not exist, both arguments are invalid and commit the existential fallacy. In regard to the second example, recall that the conclusion, which asserts that an A proposition is false, is actually a particular proposition. Thus, this example, like the first one, proceeds from the universal to the particular.

The phrase conditionally valid applies to an argument after the Aristotelian standpoint has been adopted and we are not certain if the subject term of the premise denotes actually existing things. For example, the following inference is conditionally valid:

The validity of this inference rests on whether there were in fact any students who failed the exam. The inference is either valid or invalid, but we lack sufficient information about the meaning of the premise to tell which is the case. Once it becomes known that there are indeed some students who failed the exam, we can assert that the inference is valid from the Aristotelian standpoint. But if there are no students who failed the exam, the inference is invalid because it commits the existential fallacy.

Similarly, all inference forms that depend on valid applications of contrary, subcontrary, and subalternation are conditionally valid because we do not know if the letters in the propositions denote actually existing things. For example, the following inference form, which depends on the contrary relation, is conditionally valid:

If “dogs” and “animals” are substituted in place of A and B, respectively, the resulting inference is valid. But if “unicorns” and “animals” are substituted, the resulting inference is invalid because it commits the existential fallacy. In Section 4.3, we noted that all inferences (and inference forms) that are valid from the Boolean standpoint are unconditionally valid. They are valid regardless of whether their terms denote actually existing things.

In testing an inference for validity, we are never concerned with the actual truth of the premise. Regardless of whether the premise is actually true or false, we always begin by assuming it to be true, and then we determine how this assumption bears on the truth or falsity of the conclusion. The actual truth of the premise affects only the soundness of the argument. So let us now turn to the question of soundness. Recall from Section 1.4 that a sound argument is one that is valid and has all true premises, and consider the following example:

The premise is obviously false; but if we assume it to be true, then it follows necessarily by subalternation that the conclusion is true. Thus, the inference is valid. However, because the premise is false, the inference is unsound.

Here is another example:

This inference is sound. By the contrary relation it is valid, and it also has a true premise.

 Various strategies can be used to construct proofs such as this, but one useful procedure is first to concentrate on obtaining the individual terms as they appear in the conclusion, then to attend to the order of the terms, and finally to use the square of opposition to adjust quality and quantity. As the example proof illustrates, however, variations on this procedure are sometimes necessary. The fact that the predicate of the conclusion is “A,” while “non-A” appears in the premise, leads us to think of obversion. But using obversion to change “non-A” into “A” requires that the “non-A” in the premise be moved into the predicate position via conversion. The latter operation, however, is valid only on E and I statements, and the premise is an A statement. The fact that the conclusion is a particular statement suggests subalternation as an intermediate step, thus yielding an I statement that can be converted.

 

4.6 Venn Diagrams and the Traditional Standpoint

Earlier in this chapter we saw how Venn diagrams can be used to represent the content of categorical propositions from the Boolean standpoint. With a slight modification they can also be used to represent the content of categorical propositions from the traditional, or Aristotelian, standpoint. These modified Venn diagrams can then be used to prove the relationships of the traditional square of opposition, and also to test the validity of immediate inferences from the traditional standpoint.

The difference between the Boolean standpoint and the Aristotelian standpoint concerns only universal (A and E) propositions. From the Boolean standpoint, universal propositions have no existential import, but from the Aristotelian standpoint they do have existential import when their subject terms refer to actually existing things. For example, from the Boolean standpoint the statement “All raccoons are pests” does not imply the existence of anything, but from the Aristotelian standpoint it implies the existence of raccoons. Thus, if we are to construct a Venn diagram to represent such a statement from the Aristotelian standpoint, we need to use some symbol that represents this implication of existence.

The symbol that we will use for this purpose is an X surrounded by a circle. Like the X’s that we have used up until now, this circled X signifies that something exists in the area in which it is placed. However, the two symbols differ in that the uncircled X represents the positive claim of existence made by particular (I and O) propositions, whereas the circled X represents an implication of existence made by universal propositions about actually existing things. For the purpose at hand, a circled X is placed inside the S circle as follows:

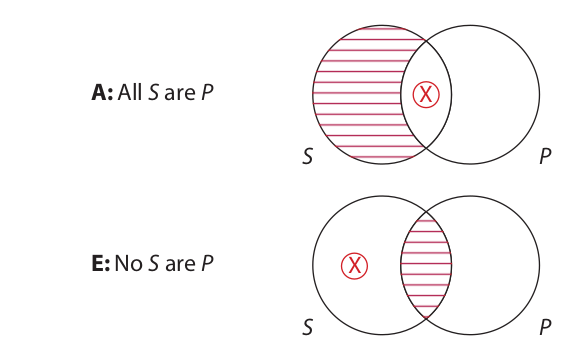
In the diagram for the A statement, the left-hand part of the S circle is shaded, so if there are any members of S, they must be in the area where the two circles overlap. Thus, a circled X is placed in the overlap area. In the diagram for the E statement, the overlap area is shaded, so if there are any members of S they must be in the left-hand part of the S circle. Thus, a circled X is placed in this area.

The diagrams for the I and O statements are the same from the Aristotelian standpoint as they are from the Boolean:

 

Proving the Traditional Square of Opposition

We can now use this modified Venn diagram technique to prove the relations of the traditional square of opposition.* Having such a proof is important because up until now these relations have only been illustrated with various examples; they have not been proved. The accompanying figure reproduces the traditional square of opposition together with Venn diagrams that represent the Aristotelian interpretation of the four standard-form propositions.

Let us begin with the contradictory relation. If the A statement is given as true, then the left-hand part of the S circle is empty. This makes the O statement false, because it claims that the left-hand part of the S circle is not empty. And if the O statement is given as true, then the left-hand part of the S circle is not empty, which makes the A statement false. On the other hand, if the O statement is given as false, then the lefthand part of the S circle is empty. However, given that some members of S exist, they must be in the overlap area. This double outcome makes the A statement true. Also, if the A statement is given as false, then either the left-hand part of the S circle is not empty, or the overlap area is empty (or both). If the left-hand part of the S circle is not empty, then the O statement is true. Alternately, if the overlap area is empty, then, given that some members of S exist, they must be in the left-hand part of the S circle, and, once again, the O statement is true. Analogous reasoning applies for the relation between the E and I statements.

Next, we turn to the contrary relation. If the A statement is given as true, then the overlap area is not empty, which makes the E statement false. By analogous reasoning, if the E statement is given as true, the overlap area is empty, which makes the A statement false. However, if the A statement is given as false (making the O statement true), then the E statement could be either true or false depending on whether or not the overlap area is empty. Thus, in this case the E statement would have logically undetermined truth value. By analogous reasoning, if the E statement is given as false (making the I statement true), the A statement could be either true or false depending on whether or not the left-hand part of the S circle is empty. Thus, the A statement would have logically undetermined truth value.

Turning next to the subcontrary relation, if the I statement is given as false, then the area where the S and P circles overlap is empty. Given that at least one S exists, there must be something in the left-hand part of the S circle, which makes the O statement true. By analogous reasoning, if the O statement is given as false, there must be something in the overlap area, making the I statement true. But if the I statement is given as true, then the O statement could be either true or false depending on whether something exists in the left-hand part of the S circle. Thus, the O statement would have undetermined truth value. Similarly, if the O statement is given as true, then the I statement could be either true or false depending on whether something exists in the overlap area. Thus, the I statement would have undetermined truth value.

Finally, we consider subalternation. If the A statement is given as true, then something exists in the area where the S and P circles overlap, which makes the I statement true as well. And if the I statement is given as false, then the overlap area is empty, making the A statement false. But if the A statement is given as false (making the O statement true), then the I statement could be either true or false depending on whether something exists in the overlap area. Thus, the I statement would have logically undetermined truth value. And if the I statement is given as true, then the A statement could be either true or false depending on whether or not the left-hand part of the S circle is empty. Thus, the A statement would have logically undetermined truth value. Analogous reasoning applies for the subalternation relation between the E and O statements.

 

Testing Immediate Inferences

From the Aristotelian standpoint, the modified Venn diagram technique involving circled X’s can be used to test immediate inferences. The only requirement is that the subject and predicate terms of the conclusion be the same as those of the premise. Such inferences depend on the square of opposition and do not involve the operations of conversion, obversion, and contraposition. Venn diagrams can also be used to test inferences involving these latter operations, but a further modification must be introduced.

Since any inference that is valid from the Boolean standpoint is also valid from the Aristotelian standpoint, testing the inference from the Boolean standpoint is often simpler. If the inference is valid, then it is valid from both standpoints. But if the inference is invalid from the Boolean standpoint and has a particular conclusion, then it may be useful to test it from the Aristotelian standpoint. Let us begin by testing an inference form for validity:

First, we draw Venn diagrams from the Boolean standpoint for the premise and conclusion:

The information of the conclusion diagram is not represented in the premise diagram, so the inference form is not valid from the Boolean standpoint. Thus, noting that the conclusion is particular, we adopt the Aristotelian standpoint and assume for the moment that the subject of the premise (A) denotes at least one existing thing. This thing is represented by placing a circled X in the open area of that circle:

Now the information of the conclusion diagram is represented in the premise diagram. Thus, the inference form is conditionally valid from the Aristotelian standpoint. It is valid on condition that the circled X represents at least one existing thing.

To test a complete inference we begin by testing its form. Here is an example:

First, we reduce the immediate inference to its form and test it from the Boolean standpoint:

Since the inference form is not valid from the Boolean standpoint, we adopt the Aristotelian standpoint and assume for the sake of this test that the subject of the premise (P) denotes at least one existing thing:

The Venn diagrams show that the inference form is conditionally valid from the Aristotelian standpoint. It is valid on condition that the circled X represents at least one existing thing. Since the circled X is in the P circle, the final step is to see if the term in the inference corresponding to P denotes something that exists. The term in question is “penguins,” and at least one penguin actually exists. Thus, the condition is fulfilled, and the inference is valid from the Aristotelian standpoint.

Another example:

This immediate inference has the same form as the first one we tested. The form is not valid from the Boolean standpoint, but it is conditionally valid from the Aristotelian standpoint:

The final step is to see if the circled X represents at least one existing thing. The circled X is in the S circle and S stands for “sugarplum fairies,” which do not exist. Thus, the requisite condition is not fulfilled, and the inference is not valid from the Aristotelian standpoint. The inference commits the existential fallacy from the Aristotelian standpoint.

The steps involved in testing an immediate inference from the Aristotelian standpoint may now be summarized:

1. Reduce the inference to its form and test it from the Boolean standpoint. If the form is valid, proceed no further. The inference is valid from both standpoints.

2. If the inference form is invalid from the Boolean standpoint and has a particular conclusion, then adopt the Aristotelian standpoint and look to see if the lefthand premise circle is partly shaded. If it is, enter a circled X in the unshaded part and retest the form.

3. If the inference form is conditionally valid, determine if the circled X represents something that exists. If it does, the condition is fulfilled, and the inference is valid from the Aristotelian standpoint. If it does not, the inference is invalid, and it commits the existential fallacy from the Aristotelian standpoint.

 

4.7 Translating Ordinary Language Statements into Categorical Form

Although few statements that occur in ordinary written and oral expression are categorical propositions in standard form, many of them can be translated into standard-form propositions. Such translation has two chief benefits. The first is that the operations and inferences pertinent to standard-form categorical propositions (contrary, subcontrary, etc.) become applicable to these statements. The second is that such statements, once translated, are completely clear and unambiguous as to their meaning. Many statements in ordinary language are susceptible to multiple interpretations, and each interpretation represents one possible mode of translation. The effort to translate such statements discloses the various interpretations and thus helps prevent misunderstanding and confusion.

Translating statements into categorical form is like any other kind of translation in that no set of specific rules will cover every possible form of phraseology. Yet, one general rule always applies: Understand the meaning of the given statement, and then reexpress it in a new statement that has a quantifier, subject term, copula, and predicate term. Some of the forms of phraseology that are typically encountered are terms without nouns, nonstandard verbs, singular propositions, adverbs and pronouns, unexpressed and nonstandard quantifiers, conditional statements, exclusive propositions, “the only,” and exceptive propositions.

 

1. Terms Without Nouns

The subject and predicate terms of a categorical proposition must contain either a plural noun or a pronoun that serves to denote the class indicated by the term. Nouns and pronouns denote classes, while adjectives (and participles) connote attributes. If a term consists of only an adjective, a plural noun or pronoun should be introduced to make the term genuinely denotative. Examples:

 

2. Nonstandard Verbs

According to the position adopted earlier in this chapter, the only copulas that are allowed in standard-form categorical propositions are “are” and “are not.” Statements in ordinary usage, however, often incorporate other forms of the verb “to be.” Such statements may be translated as the following examples illustrate:

In other statements no form of the verb “to be” occurs at all. These may be translated as the following examples indicate:

 

3. Singular Propositions

A singular proposition (statement) is a proposition that makes an assertion about a specific person, place, thing, or time. Singular propositions are typically translated into universals by means of a parameter. A parameter is a phrase that, when introduced into a statement, affects the form but not the meaning. Some parameters that may be used to translate singular propositions are these:

For example, the statement “Socrates is mortal” may be translated as “All people identical to Socrates are people who are mortal.” Because only one person is identical to Socrates, namely Socrates himself, the term “people identical to Socrates” denotes the class that has Socrates as its only member. In other words, it simply denotes Socrates. Such a translation admittedly leaves some of the original information behind, because singular statements usually have existential import, whereas universal statements do not—at least from the Boolean standpoint. But if such translations are interpreted from the Aristotelian standpoint, the existential import is preserved. Here are some examples:

In translating singular statements, note that the parameter “people identical to” is not the same as “people similar to” or “people like.” There may be many people like Socrates, but there is only one person identical to Socrates. Also note that parameters should not be used when the term in question already has a plural noun (or pronoun) that denotes the intended class. Such use is not wrong, technically, but it is redundant. Example:

 

4. Adverbs and Pronouns

When a statement contains a spatial adverb such as “where,” “wherever,” “anywhere,” “everywhere,” or “nowhere,” or a temporal adverb such as “when,” “whenever,” “anytime,” “always,” or “never,” it may be translated in terms of “places” or “times,” respectively. Statements containing pronouns such as “who,” “whoever,” “anyone,” “what,” “whatever,” or “anything” may be translated in terms of “people” or “things,” respectively. Examples:

Notice the order of the subject and predicate terms in the last four examples. When translating statements such as these it is often easy to confuse the subject term with the predicate term. However, since these statements are all translated as A type categorical propositions, such a mix-up amounts to committing the fallacy of illicit conversion. To prevent it from happening, keep this rule in mind: For “W” words (“who,” “what,” “when,” “where,” “whoever,” “whatever,” “whenever,” “wherever”), the language following the “W” word goes into the subject term of the categorical proposition.

 

5. Unexpressed Quantifiers

Many statements in ordinary usage have quantifiers that are implied but not expressed. In introducing the quantifiers one must be guided by the most probable meaning of the statement. Examples:

 

6. Nonstandard Quantifiers

In some ordinary language statements, the quantity is indicated by words other than the three standard-form quantifiers. Such words include “few,” “a few,” “not every,” “anyone,” and various other forms. Another problem occurs when the quantifier “all” is combined with the copula “are not.” As we have already seen, statements of the form “All S are not P” are not standard-form propositions. Depending on their meaning, they should be translated as either “No S are P” or “Some S are not P.” When the intended meaning is “Some S are not P,” the meaning may be indicated by placing oral emphasis on the word “all.” For example, “All athletes are not superstars” means “Some athletes are not superstars.” Here are some additional examples:

Notice that this last statement beginning with “few” cannot be translated as a single categorical proposition. Such statements (and some beginning with “a few”) must be translated as a compound arrangement of an I proposition and an O proposition. Statements beginning with “almost all” and “not quite all” must be handled in the same way. When these statements occur in arguments, the arguments must be treated in the same way as those containing exceptive propositions, which will be discussed shortly.

 

7. Conditional Statements

When the antecedent and consequent of a conditional statement refer to the same class of things, the statement can usually be translated into categorical form. Such statements are always translated as universals. Language following the word “if” goes in the subject term of the categorical proposition, and language following “only if” goes in the predicate term. Examples:

Conditional statements having a negated consequent are usually best translated as E propositions. Examples:

The word “unless” means “if not.” Since language following the word “if” goes in the subject, statements containing “unless” are translated as categorical propositions having negated subject terms. Examples:

 

8. Exclusive Propositions

Many propositions that involve the words “only,” “none but,” “none except,” and “no . . . except” are exclusive propositions. Efforts to translate them into categorical propositions often lead to confusing the subject term with the predicate term. To avoid such confusion keep in mind that language following “only,” “none but,” “none except,” and “no . . . except” goes in the predicate term of the categorical proposition. For example, the statement “Only executives can use the silver elevator” is translated “All people who can use the silver elevator are executives.” If it were translated “All executives are people who can use the silver elevator,” the translation would be incorrect. Examples:

For a statement involving “only,” “none but,” “none except,” and “no . . . except” to be a genuinely exclusive proposition, the word that follows these words must be a plural noun or pronoun. If the word that follows “only,” “none but,” or the like designates an individual, the statement really asserts two things. For example, the statement “Only Megan painted a picture” asserts that Megan painted a picture and that no other person painted a picture. Thus it would be translated as two statements: “All people identical to Megan are people who painted a picture, and all people who painted a picture are people identical to Megan.” This section of the book will ignore cases where the word following “only,” “none but,” or the like designates an individual.

Also note that many English statements containing “only” are ambiguous because “only” can be interpreted as modifying alternate words in the statement. Consider, for example, the statement “He only jogs after sunset.” Does this mean “He is the only person who jogs after sunset” or “He jogs and does not walk after sunset” or “The only time he jogs is after sunset”? If the statement’s context does not provide an answer, the translator is free to pick any of these senses for translation. This same ambiguity, incidentally, affects the last two examples in the earlier list. Accordingly, they might also be translated “All things he owns are blue-chip stocks” and “All socialites she invited are wealthy people.”

 

9. “The Only”

Statements beginning with the words “the only” are translated differently from those beginning with “only.” For example, the statement “The only cars that are available are Chevrolets” means “If a car is available, then it is a Chevrolet.” This in turn is translated as “All cars that are available are Chevrolets.” In other words, language following “the only” goes in the subject term of the categorical proposition. Examples:

Statements involving “the only” are similar to those involving “only” in this one respect: When the statement is about an individual, two statements are needed to translate it. For example, “The only person who painted a picture is Megan” means that Megan painted a picture, and no other person painted a picture. The statement is equivalent in meaning to “Only Megan painted a picture.” Thus, it is translated “All people identical to Megan are people who painted a picture, and all people who painted a picture are people identical to Megan.” Statements involving “the only” that refer to individuals are ignored throughout the remainder of this chapter.

 

10. Exceptive Propositions

Propositions of the form “All except S are P” and “All but S are P” are exceptive propositions. They must be translated not as single categorical propositions but as pairs of conjoined categorical propositions. Statements that include the phrase “none except,” on the other hand, are exclusive (not exceptive) propositions. “None except” is synonymous with “none but.” Here are some examples of exceptive propositions:

Because exceptive propositions cannot be translated into single categorical propositions, many of the simple inferences and operations pertinent to categorical propositions cannot be applied to them. Arguments that contain exceptive propositions as premises or conclusion can be evaluated only through the application of extended techniques. This topic is taken up in the next chapter.