A Concise Introduction to Logic - PART I: INFORMAL LOGIC

PART I: INFORMAL LOGIC

Chapter 1: Basic Concepts

1.1 Arguments, Premises, and Conclusions

Logic may be deﬁned as the organized body of knowledge, or science, that evaluates arguments.

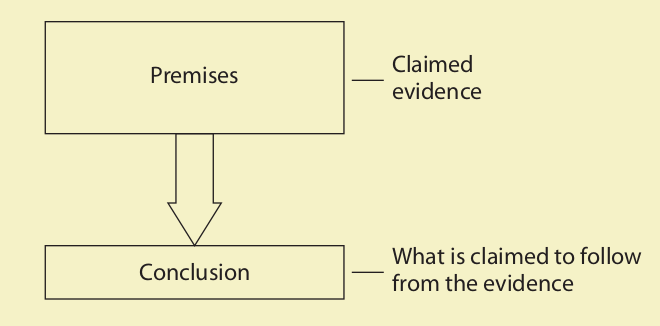
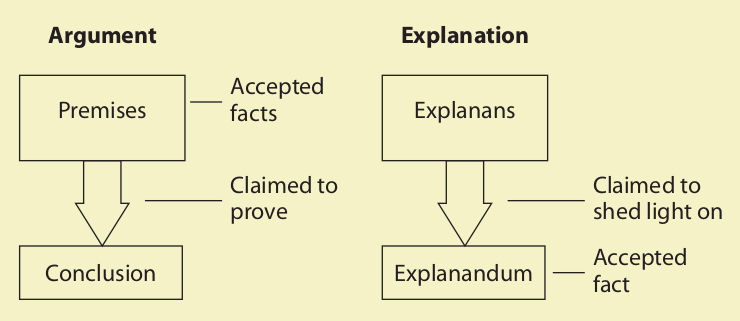
An argument, in its most basic form, is a group of statements, one or more of which (the premises) are claimed to provide support for, or reasons to believe, one of the others (the conclusion).

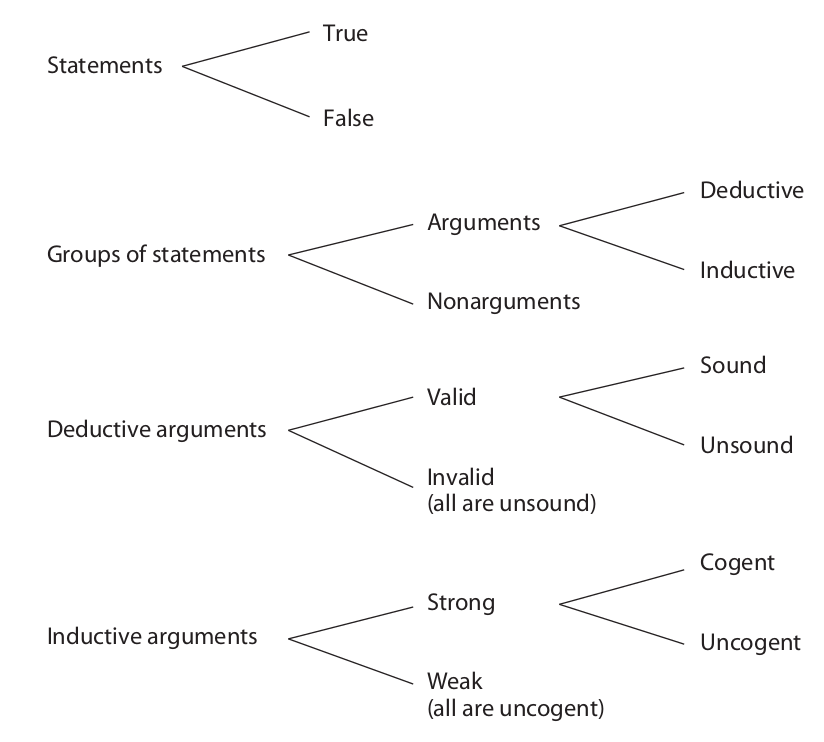
All arguments may be placed in one of two basic groups: those in which the premises really do support the conclusion and those in which they do not, even though they are claimed to. The former are said to be good arguments (at least to that extent), the latter bad arguments. The purpose of logic, as the science that evaluates arguments, is thus to develop methods and techniques that allow us to distinguish good arguments from bad.

Truth and falsity are called the two possible truth values of a statement.

The premises are the statements that set forth the reasons or evidence, and the conclusion is the statement that the evidence is claimed to support or imply. In other words, the conclusion is the statement that is claimed to follow from the premises.

conclusion indicators:

therefore
wherefore
thus
consequently
we may infer
accordingly
we may conclude
it must be that
for this reason
so
entails that
hence
it follows that
implies that
as a result

premise indicators:

since
as indicated by
because
for
in that
may be inferred from
as
given that
seeing that
for the reason that
in as much as
owing to

An inference, in the narrow sense of the term, is the reasoning process expressed by an argument. In the broad sense of the term, “inference” is used interchangeably with “argument.”

Analogously, a proposition, in the narrow sense, is the meaning or information content of a statement. For the purposes of this book, however, “proposition” and “statement” are used interchangeably.

Aristotle’s chief accomplishment is called syllogistic logic, a kind of logic in which the fundamental elements are terms, and arguments are evaluated as good or bad depending on how the terms are arranged in the argument.

But Aristotle also deserves credit for originating modal logic, a kind of logic that involves such concepts as possibility, necessity, belief, and doubt.

1.2 Recognizing Arguments

Not all passages contain arguments. Because logic deals with arguments, it is important to be able to distinguish passages that contain arguments from those that do not.
In general, a passage contains an argument if it purports to prove something; if it does not do so, it does not contain an argument. Two conditions must be fulﬁlled for a passage to purport to prove something:
1. At least one of the statements must claim to present evidence or reasons.
2. There must be a claim that the alleged evidence supports or implies something—that is, a claim that something follows from the alleged evidence or reasons.
As we have seen, the statements that claim to present the evidence or reasons are the premises, and the statement that the evidence is claimed to support or imply is the conclusion. It is not necessary that the premises present actual evidence or true
reasons nor that the premises actually support the conclusion. But at least the premises must claim to present evidence or reasons, and there must be a claim that the evidence or reasons support or imply something.
The ﬁrst condition expresses a factual claim, and deciding whether it is fulﬁlled often falls outside the domain of logic. Thus, most of our attention will be concentrated on whether the second condition is fulﬁlled. This second condition expresses
what is called an inferential claim. The inferential claim is simply the claim that the passage expresses a certain kind of reasoning process—that something supports or implies something or that something follows from something. Also, you should recognize that this claim is not equatable with the intentions of the arguer. Intentions are subjective and, as such, are usually not accessible to the evaluator. Rather, the inferential claim is an objective feature of an argument grounded in its language or structure.

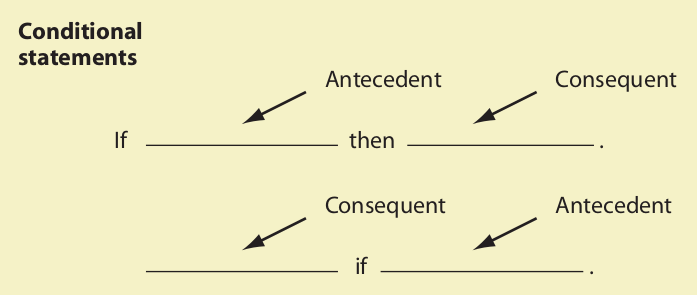
A conditional statement is an “if . . . then . . .” statement.

Every conditional statement is made up of two component statements. The component statement immediately following the “if ” is called the antecedent, and the one following the “then” is called the consequent.

A is said to be a suﬃcient condition for B whenever the occurrence of A is all that is needed for the occurrence of B. For example, being a dog is a suﬃcient condition for being an animal. On the other hand, B is said to be a necessary condition for A whenever A cannot occur without the occurrence of B. Thus, being an animal is a necessary condition for being a dog.

1.3 Deduction and Induction

A deductive argument is an argument incorporating the claim that it is impossible for the conclusion to be false given that the premises are true. Deductive arguments are those that involve necessary reasoning. On the other hand, an inductive argument is an argument incorporating the claim that it is improbable that the conclusion be false given that the premises are true. Inductive arguments involve probabilistic reasoning.

Deductive Argument Forms

An argument based on mathematics is an argument in which the conclusion depends on some purely arithmetic or geometric computation or measurement.

An argument from deﬁnition is an argument in which the conclusion is claimed to depend merely on the deﬁnition of some word or phrase used in the premise or conclusion.

A syllogism, in general, is an argument consisting of exactly two premises and one conclusion. A categorical syllogism is a syllogism in which each statement begins with one of the words “all,” “no,” or “some.”

A hypothetical syllogism is a syllogism having a conditional (“if . . . then”) statement for one or both of its premises.

A disjunctive syllogism is a syllogism having a disjunctive (“either . . . or . . .”) statement.

Inductive Argument Forms

A prediction is an argument that proceeds from our knowledge of the past to a claim about the future.

An argument from analogy is an argument that depends on the existence of an analogy, or similarity, between two things or states of aﬀairs.

A generalization is an argument that proceeds from the knowledge of a selected sample to some claim about the whole group.

An argument from authority is an argument that concludes something is true because a presumed expert or witness has said that it is.

An argument based on signs is an argument that proceeds from the knowledge of a sign to a claim about the thing or situation that the sign symbolizes.

A causal inference is an argument that proceeds from knowledge of a cause to a claim about an eﬀect, or, conversely, from knowledge of an eﬀect to a claim about a cause.

A particular statement is one that makes a claim about one or more particular members of a class, while a general statement makes a claim about all the members of a class.

1.4 Validity, Truth, Soundness, Strength, Cogency

Deductive Arguments

A valid deductive argument is an argument in which it is impossible for the conclusion to be false given that the premises are true.

An invalid deductive argument is a deductive argument in which it is possible for the conclusion to be false given that the premises are true.

A sound argument is a deductive argument that is valid and has all true premises. Both conditions must be met for an argument to be sound; if either is missing the argument is unsound.

Thus, an unsound argument is a deductive argument that is invalid, has one or more false premises, or both.

Inductive Arguments

A strong inductive argument is an inductive argument in which it is improbable that the conclusion be false given that the premises are true.

A weak inductive argument is an argument in which the conclusion does not follow probably from the premises, even though it is claimed to.

When we speak of the premises being true, we mean “true” in a complete sense. The premises must not exclude or overlook some crucial piece of evidence that undermines the stated premises and requires a diﬀerent conclusion. This proviso is otherwise called the total evidence requirement. If the total evidence requirement is not met, an argument might have literally true premises and a probably false conclusion and still be strong. Also, when we speak of the conclusion being probably false, we mean probably false in the actual world in light of all the known evidence.

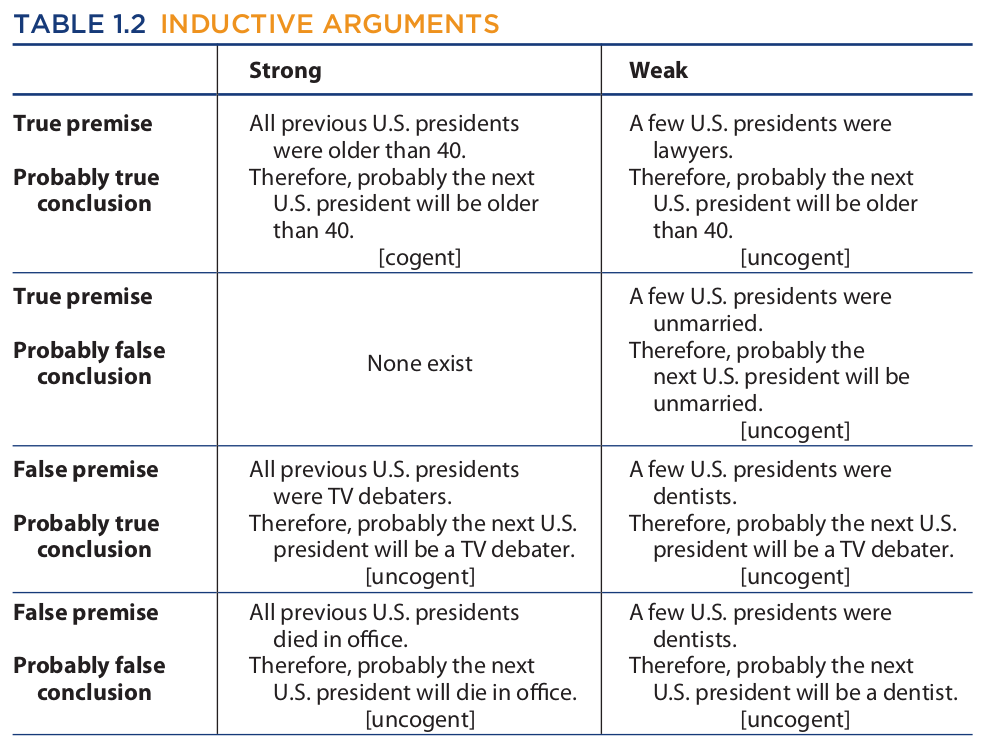
A cogent argument is an inductive argument that is strong and has all true premises. Also, the premises must be true in the sense of meeting the total evidence requirement. If any one of these conditions is missing, the argument is uncogent.

Thus, an uncogent argument is an inductive argument that is weak, has one or more false premises, fails to meet the total evidence requirement, or any combination of these.

The various alternatives open to statements and arguments may be diagrammed as follows. Note that in logic one never speaks of an argument as being “true” or “false,” and one never speaks of a statement as being “valid,” “invalid,” “strong,” or “weak.”

1.5 Argument Forms: Proving Invalidity

The validity of a deductive argument is determined by the argument form.

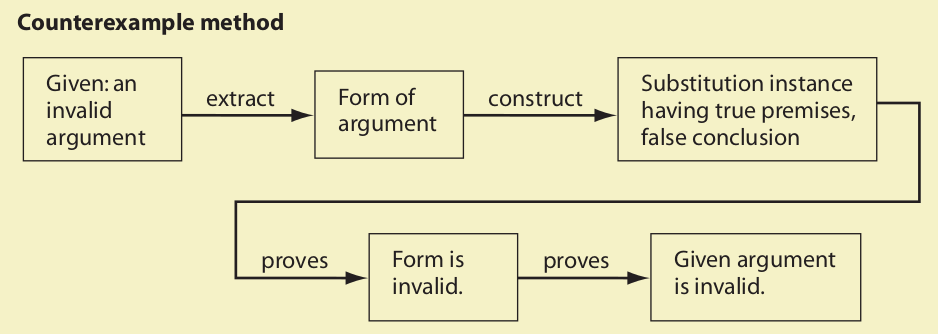
Counterexample Method

A substitution instance having true premises and a false conclusion is called a counterexample, and the method we use a counterexample to prove an argument invalid is called the counterexample method. It consists of isolating the form of an argument and then constructing a substitution instance having true premises and a false conclusion. This proves the form invalid, which in turn proves the argument invalid.

The counterexample method can be used to prove the invalidity of any invalid argument, but it cannot prove the validity of any valid argument. Thus, before the method is applied to an argument, the argument must be known or suspected to be invalid in the ﬁrst place.

Chapter 2: Language: Meaning and Definition

2.1 Varieties of Meaning

Ordinary language, as most of us are at least vaguely aware, serves various functions in our day-to-day lives. The twentieth-century philosopher Ludwig Wittgenstein thought the number of these functions to be virtually unlimited. Thus, among many other things, language is used to:

ask questions
tell stories
tell lies
guess at answers
form hypotheses
launch verbal assaults
tell jokes
flirt with someone
give directions
sing songs
issue commands
greet someone

For our purpose, two linguistic functions are particularly important: (1) to convey information and (2) to express or evoke feelings.

The ﬁrst statement is intended primarily to convey information about the death penalty, while the second is intended to persuade us that the death penalty is bad. The second accomplishes this function by engaging our feelings and not, as in an argument, by establishing the truth of a claim.

These statements accomplish their respective functions through the distinct kinds of terminology in which they are phrased. Terminology that conveys information is said to have cognitive meaning, and terminology that expresses or evokes feelings is said to have emotive meaning.

The emotively charged statement about the death penalty illustrates two important points. The ﬁrst is that statements of this sort usually have both cognitive meaning and emotive meaning. Therefore, since logic is concerned chieﬂy with cognitive
meaning, we must be able to distinguish and disengage the cognitive meaning of such statements from the emotive meaning. The second point is that part of the cognitive meaning of such statements is a value claim. A value claim is a claim that something is good, bad, right, wrong, or better or worse, more important or less important than some other thing. For example, the statement about the death penalty asserts the value claim that the death penalty is wrong or immoral. Such value claims are often the most important part of the cognitive meaning of emotive statements. Thus, for the purposes of logic, we must be able to disengage the value claims of emotively charged statements from the emotive meaning and treat these claims as separate statements.

Now that we have distinguished emotive meaning from cognitive meaning, let us explore some of the ways that cognitive meanings can be defective. Two of them are vagueness and ambiguity. A vague expression is one that allows for borderline
cases in which it is impossible to tell if the expression applies or does not apply. Vague expressions often allow for a continuous range of interpretations. The meaning is hazy, obscure, and imprecise. For example, words such as “love,” “happiness,” “peace,” “excessive,” “fresh,” “rich,” “poor,” “normal,” “conservative,” and “polluted” are vague. We can rarely tell with any precision whether they apply to a given situation or not. How fresh does something have to be in order to be called fresh?

Vagueness can also aﬀect entire statements. Such vagueness may arise not so much from the individual words as from the way in which the words are combined. For example, suppose someone were to say, “Today our job situation is more transparent.” First, what is the meaning of “job situation”? Does it refer to ﬁnding a job, keeping a job, ﬁlling a job, completing a job, or bidding on a job? And what exactly does it mean for a job situation to be “transparent”? Does it mean that the job is more easily perceived or comprehended? That the job is more easily completed? That we can anticipate our future job needs more clearly? Or what else?

Not all cases of vagueness, however, are problematic. To describe an acquaintance as “tall” or “thin” often causes no trouble in ordinary conversation. Indeed, it may be burdensome to describe this person in more precise language. Trouble arises only when the language is not sufficiently precise for what the situation demands.

The other way in which cognitive meanings can be defective is ambiguity. An ambiguous expression is one that can be interpreted as having more than one clearly distinct meaning in a given context. For example, words such as “light,” “proper,” “critical,” “stress,” “mad,” “inﬂate,” “chest,” “bank,” “sound,” and “race” can be used ambiguously. Thus, if one were to describe a beer as a light pilsner, does this mean that the beer is light in color, light in calories, or light in taste? If one were to describe an action as proper, does this mean proper in a moral sense or proper in the sense of being socially acceptable? Or if one were to describe a person as critical, does this mean that the person is essential for a certain task or that the person tends to criticize others?

As is the case with vagueness, ambiguity can also affect entire statements. Such ambiguity often results from the way in which certain words are combined. For example, there was a newspaper headline that read, “Tuna are biting oﬀ the Washington
coast.” Does this mean that the tuna are nibbling away at the coastline or that ﬁshermen are catching them oﬀ the coast? Presumably it means the latter. Another headline read, “College students are turning to vegetables.” Does this mean that the students are metamorphosing into vegetables or that they are incorporating more vegetables into their diet? Again, the intended meaning is probably the latter.

The diﬀerence between ambiguity and vagueness is that vague terminology allows for a relatively continuous range of interpretations, whereas ambiguous terminology allows for multiple discrete interpretations. A vague expression creates a blur of meaning, whereas an ambiguous expression mixes up otherwise clear meanings. However, many forms of expression are ambiguous in one context and vague in another. For example, the word “slow” in one context could mean either mentally retarded or physically slow, but when the word refers to physical slowness, it could be vague. How slow is slow? Similar remarks apply to “light,” “fast,” and “rich.”

Ambiguity and vagueness are important in logic because there are countless occasions in which the evaluation of an argument leads to the observation, “Well, that depends on what you mean by . . .” Certain phraseology in the argument is vague or ambiguous, and its meaning must be clariﬁed before any evaluation can proceed. For example, Scientologists argue that their organization should be exempt from paying taxes because, they claim, Scientology is a religion. Evaluating their argument requires that we clarify the meaning of “religion.” Pro-life advocates argue that abortion is wrong because it results in the killing of human beings. But what is the meaning of “human being”? And some feminists argue that leering glances constitute sexual harassment. To evaluate their arguments we must clarify the meaning of “leering glances” and “sexual harassment.”

The role of vagueness and ambiguity in arguments may be conveniently explored in the context of conﬂicting arguments between individuals. Such conﬂicts are called disputes:

Here the problem surrounds the vagueness of the words “abuse” and “discipline.” When does discipline become abuse? The line separating the two is hazy at best, but unless it is clariﬁed, disputes of this sort will never be resolved. Another example:

In this case the dispute arises over the ambiguity of the word “guilty.” Brenda is using the word in the moral sense. Given that Smiley has admitted to setting ﬁre to the old schoolhouse, it is very likely that he did indeed set ﬁre to it and therefore is guilty of arson in the moral sense of the term. Warren, on the other hand, is using the word in the legal sense. Because Smiley has not been convicted in a court of law, he is not legally guilty of anything.

Disputes that arise over the meaning of language are called verbal disputes. But not all disputes are of this sort. Some disputes arise over a disagreement about facts, and these are called factual disputes. Example:

Here the dispute centers on the factual issues of whether Barbara told the truth and whether Freddie stole the computer.

In dealing with disputes, the ﬁrst question is whether the dispute is factual, verbal, or some combination of the two. If the dispute is verbal, then the second question to be answered is whether the dispute concerns ambiguity or vagueness.

2.2 The Intension and Extension of Terms

The basic units of any ordinary language are words. Our main concern in this chapter, however, is not with words in general but with terms. A term is any word or arrangement of words that may serve as the subject of a statement. Terms consist of proper names, common names, and descriptive phrases. Here are some examples:

Words that are not terms include verbs, nonsubstantive adjectives, adverbs, prepositions, conjunctions, and all nonsyntactic arrangements of words.

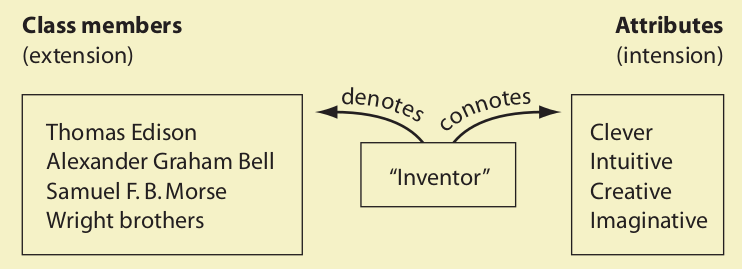
The cognitive meaning of terms comprises two kinds: intensional and extensional. The intensional meaning, or intension, consists of the qualities or attributes that the term connotes, and the extensional meaning, or extension, consists of the members of the class that the term denotes. For example, the intensional meaning of the term “cat” consists of the attributes of being furry, of having four legs, of moving in a certain way, of emitting certain sounds, and so on, while the extensional meaning consists of cats themselves—all the cats in the universe. The term connotes the attributes and denotes the cats.

The intensional meaning of a term is otherwise known as the connotation, and the extensional meaning is known as the denotation. Intension and extension are roughly equivalent to the more modern terms sense and reference, respectively. Also, note that logic uses the terms connotation and denotation diﬀerently from the way they are used in grammar. In grammar, connotation refers to the subtle nuances of a word, whereas denotation refers to the word’s direct and speciﬁc meaning.

Exactly how a term connotes a set of attributes allows for at least two diﬀerent interpretations. Some philosophers take an objective approach and hold that a term connotes whatever attributes something must have in order to be denoted by the term. Others take what might be called a subjective approach and hold that a term connotes the attributes that occur in the minds of the people who use that term. This book takes the latter approach.

In connection with this approach, however, we encounter the problem of terms connoting diﬀerent things to diﬀerent people. Thus, to a cat lover the term “cat” might connote the attributes of being cuddly and adorable, while to someone who hates cats it might connote the attributes of being obnoxious and disgusting. To avoid this problem, we restrict the meaning of connotation to what is usually called the conventional connotation. The conventional connotation of a term includes the attributes that the term commonly calls forth in the minds of competent speakers of the language. Under this interpretation, the connotation of a term remains more or less the same from person to person and from time to time.

The denotation of a term also typically remains the same from person to person, but it may change over time. The denotation of “currently living cat,” for example, is constantly ﬂuctuating as some cats die and others are born. The denotation of the term “cat,” on the other hand, is presumably constant because it denotes all cats—past, present, and future.

Sometimes the denotation of a term can change radically with the passage of time. The terms “currently living dodo bird” and “current king of France,” for example, at one time denoted actually existing entities, but today all such entities have perished. Accordingly, these terms now have what is called empty extension. They are said to denote the empty (or “null”) class, the class that has no members. Other terms with empty extension include “unicorn,” “leprechaun,” “gnome,” “elf,” and “griffin.” While these terms have empty extension, however, they do not have empty intension. “Currently living dodo bird” and “current king of France,” as well as “unicorn,” “elf,” and “griﬃn,” connote a variety of intelligible attributes.

The fact that some terms have empty extension leads us to an important connection between extension and intension—namely, that intension determines extension. The intensional meaning of a term serves as the criterion for deciding what the extension consists of. Because we know the attributes connoted by the term “unicorn,” for example, we know that the term has empty extension. That is, we know that there are no four-legged mammals having a single straight horn projecting from their forehead. Similarly, the intension of the word “cat” serves as the criterion for determining what is and what is not a member of the class of cats.

One kind of term that raises problems for the intension-determines-extension rule is proper names. For example, the name “David” might not appear to have any intension, but it denotes the person who has this name. Although philosophers have disagreed about this, it would seem that proper names must have some kind of intension or we would not know what persons, if any, they denote. One possible solution to this problem is that names are shorthand symbols for descriptions or bundles of descriptions. For example, “David” could be shorthand for “the person who lives next door” or “the person who works at the corner store and who drives a green Chevy.”

Another possible solution to the problem of proper names is that the intension of proper names consists of the causal chain of events leading from the point at which the name is ﬁrst assigned to the point at which a certain person learns about the name. Thus, the ﬁrst link in such a chain might be the baptismal event at which the name “David” is given to a certain infant, the second link would be the event in which a certain third party is informed of the ﬁrst event, and so on. This entire chain of events extending through the linguistic community would then constitute the intension of “David.” Thus, we conclude that for all terms, including proper names, intension determines extension.

The distinction between intension and extension may be further illustrated by comparing the way in which these concepts can be used to give order to random sequences of terms. Terms may be put in the order of increasing intension, increasing extension, decreasing intension, and decreasing extension. A series of terms is in the order of increasing intension when each term in the series (except the ﬁrst) connotes more attributes than the one preceding it. In other words, each term in the series after the ﬁrst is more speciﬁc than the one preceding it. (A term is speciﬁc to the degree that it connotes more attributes.) The order of decreasing intension is the reverse of that of increasing intension.

A series of terms is in the order of increasing extension when each term in the series (except the ﬁrst) denotes a class having more members than the class denoted by the term preceding it. In other words, the class size gets larger with each successive term. Decreasing extension is, of course, the reverse of this order. Examples:

These examples illustrate a fact pertaining to most such series: The order of increasing intension is usually the same as that of decreasing extension. Conversely, the order of decreasing intension is usually the same as that of increasing extension. There are some exceptions, however. Consider the following series:

Each term in this series has empty extension; so, while the series exhibits the order of increasing intension, it does not exhibit the order of decreasing extension. Here is another, slightly diﬀerent, example:

In this series none of the terms has empty extension, but each term has exactly the same extension as the others. Thus, while the intension increases with each successive term, once again the extension does not decrease.

2.3 Definitions and Their Purposes

Over the years philosophers have held various conﬂicting views about the purpose of deﬁnitions. For example, Plato claimed that deﬁnitions were intended to explicate the meaning of certain eternal essences or forms, such as justice, piety, and virtue. For most logicians today, however, deﬁnitions are intended exclusively to explicate the meaning of words. In conformity with this latter position, we may deﬁne deﬁnition as a group of words that assigns a meaning to some word or group of words. Accordingly, every deﬁnition consists of two parts: the deﬁniendum and the deﬁniens. The deﬁniendum is the word or group of words that is supposed to be deﬁned, and the deﬁniens is the word or group of words that does the deﬁning.

Stipulative Deﬁnitions

A stipulative deﬁnition assigns a meaning to a word for the ﬁrst time. This may involve either coining a new word or giving a new meaning to an old word. The purpose of a stipulative deﬁnition is usually to replace a more complex expression witha simpler one.

The need for a stipulative deﬁnition is often occasioned by some new phenomenon or development. For example, many years ago lions were crossbred with tigers. The word “tigon” was selected to name the oﬀspring of male tiger and a female lion, and “liger” was selected to name the oﬀspring of a male lion and a female tiger. When a zebra was crossbred with a donkey, the oﬀspring was called a “zeedonk.” Crossbreeding a lime with a kumquat produced a fruit that was called a “limequat,” and crossbreeding a plum with an apricot produced a fruit called a “plumcot” and a “plout.” All of these words were ﬁrst assigned their meanings through stipulative deﬁnitions.

Another use for stipulative deﬁnitions is to set up secret codes. For example, during World War II, “Tora! Tora! Tora!” was the Japanese code name that triggered the attack on Pearl Harbor. “Wotan” was the German code name for a radar system; “Golfplatz” signiﬁed Great Britain; and “Operation Sealion” was the plan to invade Great Britain. “Operation Crossbow” was the British code name for countermeasures against the V-2 rocket; “Manhattan Project” signiﬁed the American eﬀort to develop the atomic bomb; and “Operation Overlord” was the code name for the planned invasion of Normandy. More recently, corporations have employed code names to keep their projects secret from competitors. Intel has named its central processing units “Willamette,” “Deschutes,” and “Clackamas”—all of them pertinent to Oregon, where the units were designed. And Apple has named its operating systems after big cats: “Jaguar,” “Tiger,” and “Panther.”

Because a stipulative deﬁnition is a completely arbitrary assignment of a meaning to a word for the ﬁrst time, there can be no such thing as a “true” or “false” stipulative deﬁnition. Furthermore, for the same reason, a stipulative deﬁnition cannot provide any new information about the subject matter of the deﬁniendum. The fact that the word “tigon” was selected to replace “oﬀspring of a male tiger and a female lion” tells us nothing new about the nature of the animal in question. One stipulative deﬁnition may, however, be more or less convenient or more or less appropriate than another.

Stipulative deﬁnitions are misused in verbal disputes when one person covertly uses a word in a peculiar way and then proceeds to assume that everyone else uses that word in the same way. Under these circumstances that person is said to be using the word “stipulatively.” In such cases the assumption that other persons use the word in the same way is rarely justiﬁed.

Lexical Deﬁnitions

A lexical deﬁnition is used to report the meaning that a word already has in a language. Dictionary deﬁnitions are all instances of lexical deﬁnitions.

Precising Deﬁnitions

The purpose of a precising deﬁnition is to reduce the vagueness of a word. As we saw in the ﬁrst section of this chapter, an expression is vague if there are borderline cases in which it is impossible to tell if the word applies or does not apply. Words such as “fresh,” “rich,” and “poor” are vague. Once the vagueness of such words is reduced by a precising deﬁnition, one can reach a decision as to the applicability of the word to a speciﬁc situation. For example, if legislation were ever introduced to give direct ﬁnancial assistance to the poor, a precising deﬁnition would have to be supplied specifying exactly who is poor and who is not. The deﬁnition “‘Poor’ means having an annual income of less than $4,000 and a net worth of less than $20,000” is an example of a precising deﬁnition.

Whenever words are taken from ordinary usage and used in a highly systematic context such as science, mathematics, medicine, or law, they must always be clariﬁed by means of a precising deﬁnition. The terms “force,” “energy,” “acid,” “element,” “number,” “equality,” “contract,” and “agent” have all been given precising deﬁnitions by speciﬁc disciplines.

A precising deﬁnition diﬀers from a stipulative deﬁnition in that the latter involves a purely arbitrary assignment of meaning, whereas the assignment of meaning in a precising deﬁnition is not at all arbitrary. A great deal of care must be taken to ensure that the assignment of meaning in a precising deﬁnition is appropriate and legitimate for the context within which the term is to be employed.

Theoretical Deﬁnitions

A theoretical deﬁnition assigns a meaning to a word by suggesting a theory that gives a certain characterization to the entities that the term denotes. Such a deﬁnition provides a way of viewing or conceiving these entities that suggests deductive consequences, further investigation (experimental or otherwise), and whatever else would be entailed by the acceptance of a theory governing these entities. The deﬁnition of the term “heat” found in texts dealing with the kinetic theory of heat provides a good example: “‘Heat’ means the energy associated with the random motion of the molecules of a substance.” This deﬁnition does more than merely assign a meaning to a word; it provides a way of conceiving the physical phenomenon that is heat. In so doing, it suggests the deductive consequence that as the molecules of a substance speed up, the temperature of the substance increases. In addition, it suggests a number of experiments—experiments investigating the relationship between molecular velocity and the phenomena of radiation, gas pressure, molecular elasticity, and molecular conﬁguration. In short, this deﬁnition of “heat” provides the impetus for an entire theory about heat.

Other examples of theoretical deﬁnitions are the deﬁnition of “light” as a form of electromagnetic radiation and the deﬁnition of “force,” “mass,” and “acceleration” in Newton’s second law of motion as expressed in the equation “F = MA.” The latter is a kind of contextual deﬁnition in which each term is deﬁned in terms of the other two. Both deﬁnitions entail numerous deductive consequences about the phenomena involved and suggest numerous avenues of experimental investigation.

Not all theoretical deﬁnitions are associated with science. Many terms in philosophy, such as “substance,” “form,” “cause,” “change,” “idea,” “good,” “mind,” and “God,” have been given theoretical definitions. In fact, most of the major philosophers in history have given these terms their own peculiar theoretical deﬁnitions, and this fact accounts in part for the unique character of their respective philosophies. For example, Gottfried Wilhelm Leibniz’s deﬁnition of “substance” in terms of what he called “monads” laid the foundation for his metaphysical theory, and John Stuart Mill’s deﬁnition of “good” as the greatest happiness of the greatest number provided the underpinnings for his utilitarian theory of ethics.

Like stipulative deﬁnitions, theoretical deﬁnitions are neither true nor false, strictly speaking. The reason is that theoretical definitions function as proposals to see or interpret some phenomenon in a certain way. Since proposals have no truth value, neither do theoretical deﬁnitions. They may, however, be more or less interesting or more or less fruitful, depending on the deductive consequences they entail and on the outcome of the experiments they suggest.

Persuasive Deﬁnitions

The purpose of a persuasive deﬁnition is to engender a favorable or unfavorable attitude toward what is denoted by the deﬁniendum. This purpose is accomplished by assigning an emotionally charged or value-laden meaning to a word while making it appear that the word really has (or ought to have) that meaning in the language in which it is used. Thus, persuasive deﬁnitions amount to a certain synthesis of stipulative, lexical, and, possibly, theoretical deﬁnitions backed by the rhetorical motive to engender a certain attitude. As a result of this synthesis, a persuasive deﬁnition masquerades as an honest assignment of meaning to a term while condemning or blessing with approval the subject matter of the deﬁniendum. Here are some examples of opposing pairs of persuasive deﬁnitions:

The objective of a persuasive deﬁnition is to inﬂuence the attitudes of the reader or listener; thus, such deﬁnitions may be used with considerable eﬀectiveness in political speeches and editorial columns. While persuasive deﬁnitions may, like lexical deﬁnitions, be evaluated as either true or false, the primary issue is neither truth nor falsity but the eﬀectiveness of such deﬁnitions as instruments of persuasion.

2.4 Definitional Techniques

Extensional (Denotative) Deﬁnitions

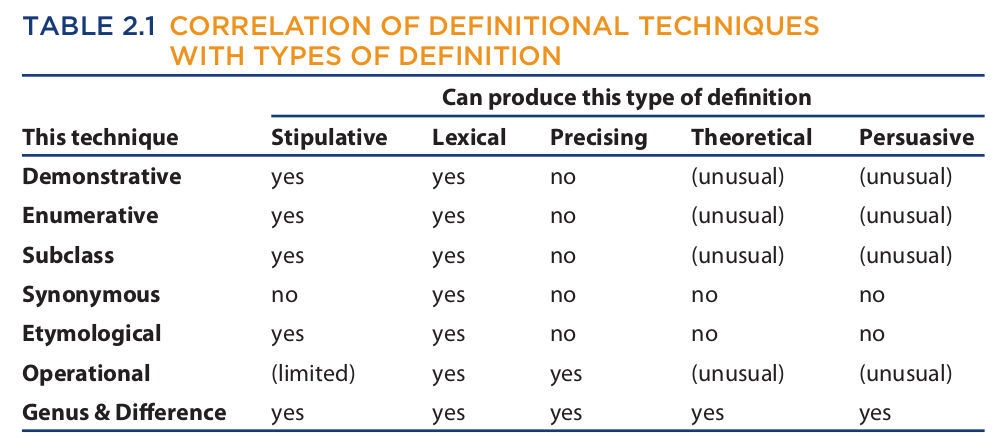
An extensional (denotative) deﬁnition is one that assigns a meaning to a term by indicating the members of the class that the deﬁniendum denotes. There are at least three ways of indicating the members of a class: pointing to them, naming them individually, and naming them in groups. The three kinds of deﬁnitions that result are called, respectively, demonstrative or ostensive deﬁnitions, enumerative deﬁnitions, and deﬁnitions by subclass.

Demonstrative (ostensive) deﬁnitions are probably the most primitive form of deﬁnition. All one need know to understand such a deﬁnition is the meaning of pointing.

Enumerative deﬁnitions assign a meaning to a term by naming the members of the class the term denotes. Like demonstrative deﬁnitions, they may also be either partial or complete.

A deﬁnition by subclass assigns a meaning to a term by naming subclasses of the class denoted by the term. Such a deﬁnition, too, may be either partial or complete, depending on whether the subclasses named, when taken together, include all the members of the class or only some of them. Examples:

The ﬁrst two are partial, the second two complete.

Intensional (Connotative) Deﬁnitions

An intensional deﬁnition is one that assigns a meaning to a word by indicating the qualities or attributes that the word connotes. Because at least four strategies may be used to indicate the attributes a word connotes, there are at least four kinds of in tensional deﬁnitions: synonymous deﬁnition, etymological deﬁnition, operational deﬁnition, and deﬁnition by genus and diﬀerence.

A synonymous deﬁnition is one in which the deﬁniens is a single word that connotes the same attributes as the deﬁniendum. In other words, the deﬁniens is a synonym of the word being deﬁned.

An etymological deﬁnition assigns a meaning to a word by disclosing the word’s ancestry in both its own language and other languages. Most ordinary English words have ancestors either in old or middle English or in some other language such as Greek, Latin, or French, and the current English meaning (as well as spelling and pronunciation) is often closely tied to the meaning (and spelling and pronunciation) of these ancestral words. For example, the English word “license” is derived from the Latin verb licere, which means to be permitted, and the English word “captain” derives from the Latin noun caput, which means head.

An operational deﬁnition assigns a meaning to a word by specifying certain experimental procedures that determine whether or not the word applies to a certain thing. Examples:

A deﬁnition by genus and diﬀerence assigns a meaning to a term by identifying a genus term and one or more diﬀerence words that, when combined, convey the meaning of the term being deﬁned. Deﬁnition by genus and diﬀerence is more generally applicable and achieves more adequate results than any of the other kinds of intensional deﬁnition. To explain how it works, we must ﬁrst explain the meanings of the terms genus, species, and speciﬁc diﬀerence.

In logic, genus and species have a somewhat diﬀerent meaning than they have in biology. In logic, genus simply means a relatively larger class, and species means a relatively smaller subclass of the genus. For example, we may speak of the genus animal and the species mammal, or of the genus mammal and the species feline, or of the genus feline and the species tiger, or the genus tiger and the species Bengal tiger. In other words, genus and species are merely relative classiﬁcations.

The speciﬁc diﬀerence, or diﬀerence, is the attribute or attributes that distinguish the various species within a genus. For example, the speciﬁc diﬀerence that distinguishes tigers from other species in the genus feline would include the attributes of being large, striped, ferocious, and so on. Because the speciﬁc diﬀerence is what distinguishes the species, when a genus is qualiﬁed by a speciﬁc diﬀerence, a species is identiﬁed. Deﬁnition by genus and diﬀerence is based on this fact. It consists of combining a term denoting a genus with a word or group of words connoting a speciﬁc diﬀerence so that the combination identiﬁes the meaning of the term denoting the species.

A deﬁnition by genus and diﬀerence is easy to construct. Simply select a term that is more general than the term to be deﬁned, then narrow it down so that it means the same thing as the term being deﬁned. Examples:

2.5 Criteria for Lexical Definitions

Because the function of a lexical deﬁnition is to report the way a word is actually used in a language, lexical deﬁnitions are the ones we most frequently encounter and are what most people mean when they speak of the “deﬁnition” of a word. Accordingly, it is appropriate that we have a set of rules that we may use in constructing lexical deﬁnitions of our own and in evaluating the lexical deﬁnitions of others. While some of these rules apply to the other kinds of deﬁnitions as well, the unique functions that are served by stipulative, precising, theoretical, and persuasive deﬁnitions prescribe diﬀerent sets of criteria.

Rule 1: A Lexical Definition Should Conform to the Standards of Proper Grammar

Rule 2: A Lexical Definition Should Convey the Essential Meaning of the Word Being Defined

Rule 3: A Lexical Definition Should Be Neither Too Broad nor Too Narrow

Rule 4: A Lexical Definition Should Avoid Circularity

Rule 5: A Lexical Definition Should Not Be Negative When It Can Be Affirmative

Rule 6: A Lexical Definition Should Avoid Figurative, Obscure, Vague, or Ambiguous Language

Rule 7: A Lexical Definition Should Avoid Affective Terminology

Rule 8: A Lexical Definition Should Indicate the Context to Which the Definiens Pertains

Chapter 3: Informal Fallacies

3.1 Fallacies in General

A fallacy is a defect in an argument that consists in something other than false premises alone. Both deductive and inductive arguments may contain fallacies; if they do, they are either unsound or uncogent, depending on the kind of argument. Conversely, if an argument is unsound or uncogent, it has one or more false premises or it contains a fallacy (or both).

Fallacies are usually divided into two groups: formal and informal.

A formal fallacy is one that may be identiﬁed by merely examining the form or structure of an argument. Fallacies of this kind are found only in deductive arguments that have identiﬁable forms.

Informal fallacies are those that can be detected only by examining the content of the argument. Consider the following example:

To detect this fallacy one must know something about bridges—namely, that they are large visible objects, and even though their atomic components are invisible, this does not mean that the bridges themselves are invisible.

3.2 Fallacies of Relevance

The fallacies of relevance share the common characteristic that the arguments in which they occur have premises that are logically irrelevant to the conclusion. Yet the premises may appear to be psychologically relevant, so the conclusion may seem to follow from the premises, even though it does not follow logically.

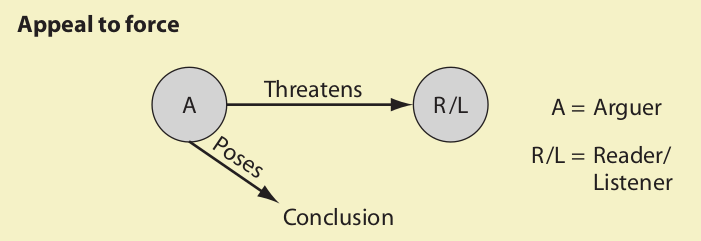
1. Appeal to Force

The fallacy of appeal to force occurs whenever an arguer poses a conclusion to another person and tells that person either implicitly or explicitly that some harm will come to him or her if he or she does not accept the conclusion. The fallacy always involves a threat by the arguer to the physical or psychological well-being of the listener or reader, who may be either an individual or a group of people. Obviously, such a threat is logically irrelevant to the subject matter of the conclusion, so any argument based on such a procedure is fallacious.

2. Appeal to Pity

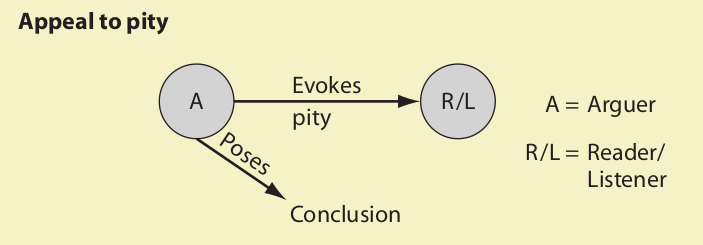
The appeal to pity fallacy occurs when an arguer attempts to support a conclusion by merely evoking pity from the reader or listener. This pity may be directed toward the arguer or toward some third party.

3. Appeal to the People

Nearly everyone wants to be loved, esteemed, admired, valued, recognized, and accepted by others. The appeal to the people uses these desires to get the reader or listener to accept a conclusion. Two approaches are involved: one of them direct, the other indirect.

The direct approach occurs when an arguer, addressing a large group of people, excites the emotions and enthusiasm of the crowd to win acceptance for his or her conclusion. The objective is to arouse a kind of mob mentality. This is the strategy used by nearly every propagandist and demagogue. An appeal to negative emotions, such as suspicion and fear, can also generate a mob mentality. These emotions have produced many lynchings, and they led to the internment of Japanese Americans during World War II.

In the indirect approach the arguer aims his or her appeal not at the crowd as a whole but at one or more individuals separately, focusing on some aspect of their relationship to the crowd. The indirect approach includes such speciﬁc forms as the bandwagon argument, the appeal to vanity, and the appeal to snobbery. All are standard techniques of the advertising industry.

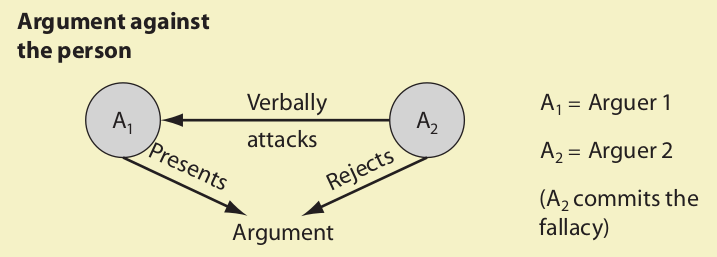
4. Argument Against the Person

This fallacy always involves two arguers. One of them advances (either directly or implicitly) a certain argument, and the other then responds by directing his or her attention not to the ﬁrst person’s argument but to the ﬁrst person himself. When this occurs, the second person is said to commit an argument against the person.

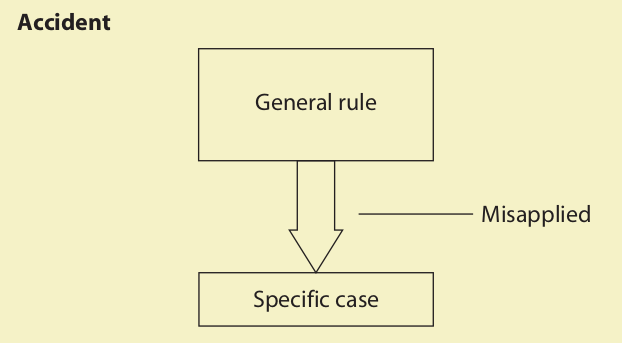
5. Accident

The fallacy of accident is committed when a general rule is applied to a speciﬁc case it was not intended to cover. Typically, the general rule is cited (either directly or implicitly) in the premises and then wrongly applied to the speciﬁc case mentioned in the conclusion. Two examples:

In the ﬁrst example, the general rule is that freedom of speech is normally guaranteed, and the speciﬁc case is the speech made by John Q. Radical. Because the speech incited a riot, the rule does not apply. In the second example, the general rule is that people are obligated to keep their promises, and the speciﬁc case is that Jessica should keep her promise to stay with Tyler. The rule does not apply because Tyler is no longer the same person that Jessica made her promise to.

6. Straw Man

The straw man fallacy is committed when an arguer distorts an opponent’s argument for the purpose of more easily attacking it, demolishes the distorted argument, and then concludes that the opponent’s real argument has been demolished. By so doing, the arguer is said to have set up a straw man and knocked it down, only to conclude that the real man (opposing argument) has been knocked down as well. Example:

Like the argument against the person fallacy, the straw man fallacy involves two arguers. Mr. Goldberg, who is the ﬁrst arguer, has presented an argument against prayer in the public schools. The second arguer then attacks Goldberg’s argument by equating it with an argument for atheism. He then attacks atheism and concludes that Goldberg’s argument is nonsense. Since Goldberg’s argument had nothing to do with atheism, the second argument commits the straw man fallacy.

As this example illustrates, the kind of distortion the second arguer resorts to is often an attempt to exaggerate the ﬁrst person’s argument or make it look more extreme than it really is.

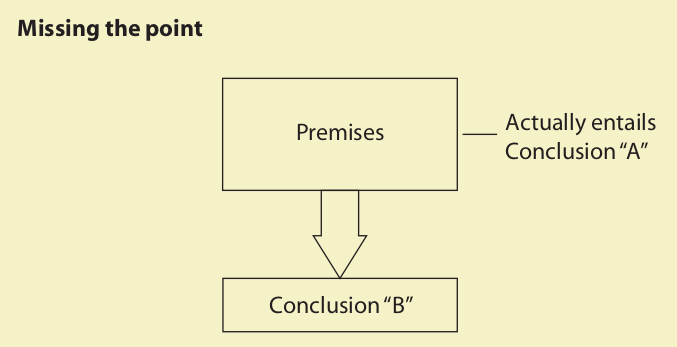
7. Missing the Point

All the fallacies we have discussed thus far have been instances of cases where the premises of an argument are irrelevant to the conclusion. Missing the point illustrates a special form of irrelevance. This fallacy occurs when the premises of an argument support one particular conclusion, but then a diﬀerent conclusion, often vaguely related to the correct conclusion, is drawn. Whenever one suspects that such a fallacy

is being committed, he or she should be able to identify the correct conclusion, the conclusion that the premises logically imply. This conclusion must be signiﬁcantly different from the conclusion that is actually drawn. Examples:

At least two correct conclusions are implied by the premise of the ﬁrst argument: either “We should provide increased police protection in vulnerable neighborhoods” or “We should initiate programs to eliminate the causes of the crimes.” Reinstating the death penalty is not a logical conclusion at all. Among other things, theft and robbery are not capital crimes. In the second argument the premises logically suggest some systematic eﬀort to eliminate the cheaters rather than eliminating the system altogether.

The arguer is ignorant of the logical implications of his or her own premises and, as a result, draws a conclusion that misses the point entirely. The fallacy has a distinct structure all its own, but in some ways it serves as a catchall for arguments that are not clear instances of one or more of the other fallacies. An argument should not be identiﬁed as a case of missing the point, however, if one of the other fallacies ﬁts.

8. Red Herring

This fallacy is closely associated with missing the point (ignoratio elenchi). The red herring fallacy is committed when the arguer diverts the attention of the reader or listener by changing the subject to a diﬀerent but sometimes subtly related one. He or she then ﬁnishes by either drawing a conclusion about this diﬀerent issue or by merely presuming that some conclusion has been established. By so doing, the arguer purports to have won the argument. The fallacy gets its name from a procedure used to train hunting dogs to follow a scent. A red herring (or bag of them) is dragged across the trail with the aim of leading the dogs astray. Since red herrings have an especially potent scent (caused in part by the smoking process used to preserve them), only the best dogs will follow the original scent.

To use the red herring fallacy eﬀectively, the arguer must change the original subject of the argument without the reader or listener noticing it. One way of doing this is to change the subject to one that is subtly related to the original subject. Here are two examples of this technique:

Both arguments commit the red herring fallacy. In the first, the original issue is whether nuclear power is dangerous. The arguer changes this subject to the danger of electrocution and proceeds to draw a conclusion about that. The new subject is clearly diﬀerent from the possibility of nuclear explosion or meltdown, but the fact that both are related to electricity facilitates the arguer’s goal of leading someone oﬀ the track. In the second argument, the original issue is pesticides, and the arguer changes it to the value of fruits and vegetables in one’s diet. Again, the fact that the second topic is related to the ﬁrst assists the arguer in committing the fallacy. In neither case does the arguer draw a conclusion about the original topic, but by merely diverting the attention of the reader or listener, the arguer creates the presumption of having won the argument.

A second way of using the red herring eﬀectively is to change the subject to some ﬂashy, eye-catching topic that is virtually guaranteed to distract the listener’s attention. Topics of this sort include sex, crime, scandal, immorality, death, and any other topic that might serve as the subject of gossip. Here is an example of this technique:

The red herring fallacy can be confused with the straw man fallacy because both have the eﬀect of drawing the reader/listener oﬀ the track. This confusion can usually be avoided by remembering the unique ways in which they accomplish this purpose. In the straw man, the arguer begins by distorting an opponent’s argument and concludes by knocking down the distorted argument. In the red herring, the arguer ignores the opponent’s argument (if there is one) and subtly changes the subject. Thus, to distinguish the two fallacies, one should attempt to determine whether the arguer has knocked down a distorted argument or simply changed the subject. Also keep in mind that straw man always involves two arguers, at least implicitly, whereas a red herring often does not.

Both the red herring and straw man fallacies are susceptible of being confused with missing the point, because all three involve a similar kind of irrelevancy. To avoid this confusion, one should note that both red herring and straw man proceed by generating a new set of premises, whereas missing the point does not. Straw man draws a conclusion from new premises that are obtained by distorting an earlier argument, and red herring, if it draws any conclusion at all, draws one from new premises obtained by changing the subject. Missing the point, however, draws a conclusion from the original premises. Also, in the red herring and straw man, the conclusion, if there is one, is relevant to the premises from which it is drawn; but in missing the point, the conclusion is irrelevant to the premises from which it is drawn. Finally, remember that missing the point serves in part as a kind of catchall fallacy, and a fallacious argument should not be identiﬁed as a case of missing the point if one of the other fallacies clearly ﬁts.

3.3 Fallacies of Weak Induction

The fallacies of weak induction occur not because the premises are logically irrelevant to the conclusion, as is the case with the eight fallacies of relevance, but because the connection between premises and conclusion is not strong enough to support the conclusion.

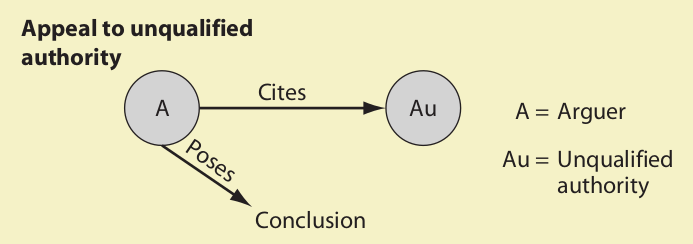
9. Appeal to Unqualiﬁed Authority

The appeal to unqualiﬁed authority fallacy is a variety of the argument from authority and occurs when the cited authority or witness lacks credibility. There are several reasons why an authority or witness might lack credibility. The person might lack the requisite expertise, might be biased or prejudiced, might have a motive to lie or disseminate “misinformation,” or might lack the requisite ability to perceive or recall.

10. Appeal to Ignorance

When the premises of an argument state that nothing has been proved one way or the other about something, and the conclusion then makes a deﬁnite assertion about that thing, the argument commits an appeal to ignorance. The issue usually involves something that is incapable of being proved or something that has not yet been proved.

The premises of an argument are supposed to provide positive evidence for the conclusion. The premises of these arguments, however, tell us nothing about astrology; rather, they tell us about what certain unnamed and unidentiﬁed people have tried unsuccessfully to do. This evidence may provide some slight reason for believing the conclusion, but certainly not suﬃcient reason.

These examples do, however, lead us to the ﬁrst of two important exceptions to the appeal to ignorance. The ﬁrst stems from the fact that if qualiﬁed researchers investigate a certain phenomenon within their range of expertise and fail to turn up any evidence that the phenomenon exists, this fruitless search by itself constitutes positive evidence about the question. Consider, for example, the following argument:

The premises of this argument are true. Given the circumstances, it is likely that the scientists in question would have detected the aether if in fact it did exist. Since they did not detect it, it probably does not exist. Thus, we can say that the given argument is inductively strong (but not deductively valid).

As for the two arguments about astrology, if the attempts to prove or disprove the astrological claims had been done in a systematic way by qualiﬁed experts, the arguments would more likely be good. Exactly what is required to qualify someone to investigate astrological claims is, of course, diﬃcult to say. But as these arguments stand, the premises state nothing about the qualiﬁcations of the investigators, and so the arguments remain fallacious.

It is not always necessary, however, that the investigators have special qualiﬁcations. The kinds of qualiﬁcations needed depend on the situation. Sometimes the mere ability to see and report what one sees is suﬃcient. Example:

Because it is highly probable that if Mr. Andrews were a drinker, somebody would have seen him drinking, this argument is inductively strong. No special qualiﬁcations are needed to be able to see someone take a drink.

The second exception to the appeal to ignorance relates to courtroom procedure. In the United States and a few other countries, a person is presumed innocent until proven guilty. If the prosecutor in a criminal trial fails to prove the guilt of the defendant beyond reasonable doubt, counsel for the defense may justiﬁably argue that his or her client is not guilty. Example:

This argument commits no fallacy because “not guilty” means, in the legal sense, that guilt beyond a reasonable doubt has not been proved. The defendant may indeed have committed the crime of which he or she is accused, but if the prosecutor fails to prove guilt beyond a reasonable doubt, the defendant is considered “not guilty.”

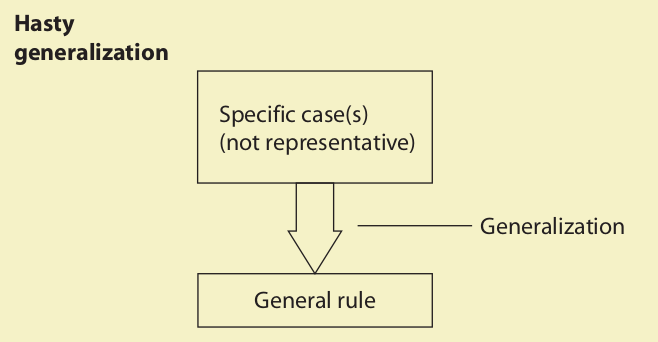
11. Hasty Generalization (Converse Accident)

Hasty generalization is a fallacy that aﬀects inductive generalizations. The fallacy occurs when there is a reasonable likelihood that the sample is not representative of the group. Such a likelihood may arise if the sample is either too small or not randomly selected.

12. False Cause

The fallacy of false cause occurs whenever the link between premises and conclusion depends on some imagined causal connection that probably does not exist. Whenever an argument is suspected of committing the false cause fallacy, the reader or listener should be able to say that the conclusion depends on the supposition that X causes Y, whereas X probably does not cause Y at all. Examples:

The ﬁrst argument depends on the supposition that the blue ribbons caused the defeats, the second on the supposition that a high salary causes success, and the third on the supposition that laws cause crime. In no case is it likely that any causal connection exists.

The ﬁrst argument illustrates a variety of the false cause fallacy called post hoc ergo propter hoc (“after this, therefore on account of this”). This variety of the fallacy presupposes that just because one event precedes another event, the ﬁrst event causes the second. Obviously, mere temporal succession is not suﬃcient to establish a causal connection. Nevertheless, this kind of reasoning is quite common and lies behind most forms of superstition. (Example: “A black cat crossed my path and later I tripped and sprained my ankle. It must be that black cats really are bad luck.”)

The second and third arguments illustrate a variety of the false cause fallacy called non causa pro causa (“not the cause for the cause”). This variety is committed when what is taken to be the cause of something is not really the cause at all and the mistake is based on something other than mere temporal succession. In reference to the second argument, success as an executive causes increases in salary— not the other way around—so the argument mistakes the cause for the eﬀect. In reference to the third argument, the increase in crime is, for the most part, only coincidental with the increase in the number of laws. Obviously, the mere fact that one event is coincidental with another is not suﬃ cient reason to think that one caused the other.

A third variety of the false cause fallacy, and one that is probably committed more often than either of the others in their pure form, is oversimpliﬁed cause. This variety occurs when a multitude of causes is responsible for a certain eﬀect but the arguer selects just one of these causes and represents it as if it were the sole cause. Here are some examples:

In reference to the first argument, the decline in the quality of education is caused by many factors, including lack of discipline in the home, lack of parental involvement, too much television, and drug use by students. Poor teacher performance is only one of these factors and probably a minor one at that. In the second argument, the eﬀorts of doctors are only one among many factors responsible for our longer life span. Other, more important factors include a better diet, more exercise, reduced smoking, safer highways, and more stringent occupational safety standards.

The oversimplified cause fallacy is usually motivated by self-serving interests. Sometimes the arguer wants to take undeserved credit for himself or herself or give undeserved credit to some movement with which he or she is aﬃliated. At other times, the arguer wants to heap blame on an opponent or shift blame from himself or herself onto some convenient occurrence. Instances of the fallacy can resemble either the post hoc or the non causa pro causa varieties in that the alleged cause can occur either prior to or concurrently with the eﬀect. It diﬀers from the other varieties of false cause fallacy in that the single factor selected for credit or blame is often partly responsible for the eﬀect, but responsible to only a minor degree.

The last variety of false cause we will consider is called the gambler’s fallacy. This fallacy is committed whenever the conclusion of an argument depends on the supposition that independent events in a game of chance are causally related. Here is an example:

In fact, it is no more likely that the coin will come up tails on the next ﬂip than it was on the ﬁrst ﬂip. Each ﬂip is an independent event, so earlier ﬂips have no causal inﬂuence on later ones. Thus, the fact that the earlier ﬂips came up heads does not increase the likelihood that the next ﬂip will come up tails.

For the gambler’s fallacy to be committed, the events must be independent or nearly independent. Such events include rolls of a pair of fair (unloaded) dice, spins of a fair roulette wheel, and selections of lottery winning numbers. Events are not completely independent whenever the skill of the gambler aﬀects the outcome. Thus, poker, blackjack, and horse-race betting provide less-than-perfect candidates for the gambler’s fallacy.

One point that should be kept in mind when establishing causal connections is that statistical correlations by themselves often reveal little about what is actually going on. For example, if all that we knew about smoking and lung cancer was that the two frequently occur together, we might conclude any number of things. We might conclude that both have a common cause, such as a genetic predisposition, or we might conclude that lung cancer is a disease contracted early in life and that it manifests itself in its early stages by a strong desire for tobacco. Fortunately, in this case we have more evidence than a mere statistical correlation. This additional evidence inclines us to believe that the smoking is a cause of the cancer.

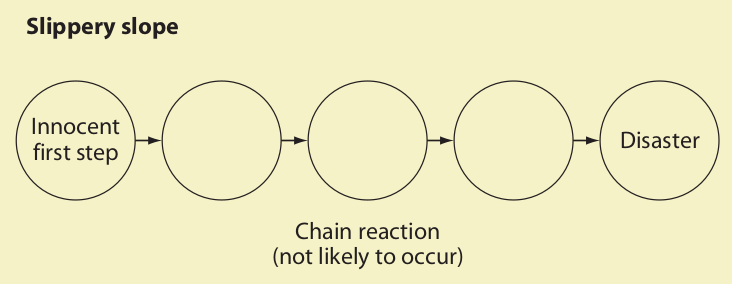
13. Slippery Slope

The fallacy of slippery slope is a variety of the false cause fallacy. It occurs when the conclusion of an argument rests on an alleged chain reaction and there is not suﬃcient reason to think that the chain reaction will actually take place.

14. Weak Analogy

This fallacy affects inductive arguments from analogy. The fallacy of weak analogy is committed when the analogy is not strong enough to support the conclusion that is drawn.

3.4 Fallacies of Presumption, Ambiguity, and Grammatical Analogy

The fallacies of presumption include begging the question, complex question, false dichotomy, and suppressed evidence. These fallacies arise not because the premises are irrelevant to the conclusion or provide insuﬃcient reason for believing the conclusion but because the premises presume what they purport to prove. Begging the question presumes that the premises provide adequate support for the conclusion when in fact they do not, and complex question presumes that a question can be answered by a simple “yes,” “no,” or other brief answer when a more sophisticated answer is needed. False dichotomy presumes that an “either . . . or . . .” statement presents jointly exhaustive alternatives when in fact it does not, and suppressed evidence presumes that no important evidence has been overlooked by the premises when in fact it has.

The fallacies of ambiguity include equivocation and amphiboly. These fallacies arise from the occurrence of some form of ambiguity in either the premises or the conclusion (or both).

The fallacies of grammatical analogy include composition and division. Arguments that commit these fallacies are grammatically analogous to other arguments that are good in every respect. Because of this similarity in linguistic structure, such fallacious arguments may appear good yet be bad.

15. Begging the Question

The fallacy of begging the question is committed whenever the arguer creates the illusion that inadequate premises provide adequate support for the conclusion by leaving out a possibly false (shaky) key premise, by restating a possibly false premise as the conclusion, or by reasoning in a circle. The Latin name for this fallacy, petitio principii, means “request for the source.” The actual source of support for the conclusion is not apparent, and so the argument is said to beg the question. After reading or hearing the argument, the observer is inclined to ask, “But how do you know X?” where X is the needed support.

The ﬁrst, and most common, way of committing this fallacy is by leaving a possibly false key premise out of the argument while creating the illusion that nothing more is needed to establish the conclusion. Examples:

The ﬁrst of these arguments begs the question “How do you know that abortion is a form of murder?” The second begs the question “Does the structure and function of the human hand and arm tell us what humans should eat?” And the third and fourth beg the questions “Just because the poor earn less than the average citizen, does this imply that the government should give them handouts?” and “Just because terminally ill patients cannot commit suicide by themselves, does it follow that they have a right to a doctor’s assistance?”

These questions indicate that something has been left out of the original arguments. Thus, the ﬁrst argument is missing the premise “Abortion is a form of murder”; the second is missing the premise “The structure and function of the human hand and arm tell us what humans should eat” and so on. These premises are crucial for the soundness of the arguments. If the arguer is unable to establish the truth of these premises, then the arguments prove nothing. However, in most cases of begging the question, this is precisely the reason why such premises are left unstated. The arguer is not able to establish their truth, and by employing rhetorical phraseology such as “of course,” “clearly,” “this being the case,” and “after all,” the arguer hopes to create the illusion that the stated premise, by itself, provides adequate support for the conclusion when in fact it does not.

The same form of begging the question often appears in arguments concerning religious topics to justify conclusions about the existence of God, the immortality of the soul, and so on. Example:

This argument begs the question “How do you know that the organization in the world could only have come from an intelligent creator?” Of course the claim that it did come from an intelligent creator may well be true, but the burden is on the arguer to prove it. Without supporting reasons or evidence, the argument proves nothing. Yet most people who are predisposed to believe the conclusion are likely to accept the argument as a good one. The same can be said of most arguments that beg the question, and this fact suggests another reason why arguers resort to this fallacy: Such arguments tend to reinforce preexisting inclinations and beliefs.

The second form of petitio principii occurs when the conclusion of an argument merely restates a possibly false premise in slightly diﬀerent language. In such an argument, the premise supports the conclusion, and the conclusion tends to reinforce the premise. Examples:

In the ﬁrst argument, saying that capital punishment is “justiﬁed” means the same thing as saying that it is “legitimate and appropriate,” and in the second argument the premise and the conclusion say exactly the same thing. However, by repeating the same thing in slightly diﬀerent language, the arguer creates the illusion that independent evidence is being presented in support of the conclusion, when in fact it is not. Both arguments contain rhetorical phraseology (“hateful and inhuman,” “simple reason,” and “could not possibly”) that help eﬀect the illusion. The ﬁrst argument begs the question “How do you know that capital punishment really is legitimate and appropriate?” and the second begs the question “How do you know that people who preach revolution really do have a vision of the future?”

The third form of petitio principii involves circular reasoning in a chain of inferences having a ﬁrst premise that is possibly false. Example:

On encountering this argument, the attentive reader is inclined to ask, “Where does this reasoning begin? What is its source?” Since the argument goes in a circle, it has no beginning or source, and as a result it proves nothing. Of course, in this example the circularity is rather apparent, so the argument is not likely to convince anyone. Cases in which circular reasoning may convince involve long and complex arguments having premises that depend on one another in subtle ways and a possibly false key premise that depends on the conclusion.

In all cases of begging the question, the arguer uses some linguistic device to create the illusion that inadequate premises provide adequate support for a conclusion. Without such an illusion, the fallacy is not committed. Thus, the following arguments commit no fallacy:

In both of these examples, the premise amounts to little more than a restatement of the conclusion. Yet both arguments are sound because they are valid and have true premises. No fallacy is committed, because no illusion is created to make inadequate premises appear as adequate.

16. Complex Question

The fallacy of complex question is committed when two (or more) questions are asked in the guise of a single question and a single answer is then given to both of them. Every complex question presumes the existence of a certain condition. When the respondent’s answer is added to the complex question, an argument emerges that establishes the presumed condition. Thus, although not an argument as such, a complex question involves an implicit argument. This argument is usually intended to trap the respondent into acknowledging something that he or she might otherwise not want to acknowledge. Examples:

Let us suppose the respondent answers “yes” to the ﬁrst question and “under the bed” to the second. The following arguments emerge:

On the other hand, let us suppose that the respondent answers “no” to the ﬁrst question and “nowhere” to the second. We then have the following arguments:

17. False Dichotomy

The fallacy of false dichotomy is committed when a disjunctive (“either . . . or . . .”) premise presents two unlikely alternatives as if they were the only ones available, and the arguer then eliminates the undesirable alternative, leaving the desirable one as the conclusion. Such an argument is clearly valid, but since the disjunctive premise is false, or at least probably false, the argument is typically unsound. The fallacy is often committed by children when arguing with their parents, by advertisers, and by adults generally. Here are three examples:

In none of these arguments does the disjunctive premise present the only alternatives available, but in each case the arguer tries to convey that impression. For example, in the first argument, the arguer tries to convey the impression that he or she either goes to the concert or faces a lifetime of misery, and that no other alternatives are possible. Clearly, however, this is not the case.

If one of the alternatives in the disjunctive premise is true, then the fallacy is not committed. For example, the following argument is valid and sound:

False dichotomy is otherwise called “false bifurcation” and the “either-or fallacy.” Also, in most cases the arguer expresses only the disjunctive premise and leaves it to the reader or listener to supply the missing statements:

The missing premise and conclusion are easily introduced.

18. Suppressed Evidence

Chapter 1 explained that a cogent argument is an inductive argument with good reasoning and true premises. The requirement of true premises includes the proviso that the premises not ignore some important piece of evidence that outweighs the presented evidence and entails a very diﬀerent conclusion. If an inductive argument does indeed ignore such evidence, then the argument commits the fallacy of suppressed evidence. Consider, for example, the following argument:

If the arguer ignores the fact that the little dog is excited and foaming at the mouth (which suggests rabies), then the argument commits a suppressed evidence fallacy. This fallacy is classiﬁed as a fallacy of presumption because it works by creating the presumption that the premises are both true and complete when in fact they are not.

Perhaps the most common occurrence of the suppressed evidence fallacy appears in inferences based on advertisements. Nearly every ad neglects to mention certain negative features of the product advertised. As a result, an observer who sees or hears an advertisement and then draws a conclusion from it may commit the fallacy of suppressed evidence. Example:

The ad fails to state that the fun does not come packaged with the chicken but must be supplied by the buyer. Also, of course, the ad fails to state that the chicken is loaded with fat and that the buyer’s resultant weight gain may not amount to a barrel of fun. By ignoring these facts, the argument based on the ad is fallacious.

Another way that an arguer can commit the suppressed evidence fallacy is by ignoring important events that have occurred with the passage of time that render an inductive conclusion improbable. Here is an example:

This argument ignores the fact that Poland was part of the Soviet bloc during most of the past sixty years, and this fact accounts for its rather low standard of living. However, following the collapse of the Soviet Union, Poland became an independent nation, and its economy is expected to improve steadily during the next sixty years.

Yet another form of suppressed evidence is committed by arguers who quote passages out of context from sources such as the Bible, the Constitution, and the Bill of Rights to support a conclusion that the passage was not intended to support. Consider, for example, the following argument against gun control:

In fact, the Second Amendment reads, “A well regulated militia being necessary to the security of a free state, the right of the people to keep and bear arms shall not be infringed.” In other words, the constitutional right to keep and bear arms is in some way related to the preservation of a well-regulated militia. Arguably a law controlling hand guns that is unrelated to the preservation of a well-regulated militia could be constitutional.

The suppressed evidence fallacy is similar to the form of begging the question in which the arguer leaves a key premise out of the argument. The diﬀerence is that suppressed evidence leaves out a premise that requires a diﬀerent conclusion, while that form of begging the question leaves out a premise that is needed to support the stated conclusion. However, because both fallacies proceed by leaving a premise out of the argument, there are cases where the two fallacies overlap.

19. Equivocation

The fallacy of equivocation occurs when the conclusion of an argument depends on the fact that a word or phrase is used, either explicitly or implicitly, in two diﬀerent senses in the argument. Such arguments are either invalid or have a false premise, and in either case they are unsound. Examples:

In the first argument “obtuse” is used in two different senses. In the first premise it describes a certain kind of angle, while in the second it means dull or stupid. The second argument equivocates on the word “law.” In the ﬁrst premise it means statutory law, and in the second it means law of nature. The third argument uses “right” in two senses. In the ﬁrst premise “right” means morally correct, but in the second it means a just claim or power. The fourth argument illustrates the ambiguous use of a relative word. The word “large” means diﬀerent things depending on the context. Other relative words that are susceptible to this same kind of ambiguity include “small,” “good,” “bad,” “light,” “heavy,” “diﬃcult,” “easy,” “tall,” and “short.”

To be convincing, an argument that commits an equivocation must use the equivocal word in ways that are subtly related. Of the examples just given, only the third might fulﬁll this requirement. Since both uses of the word “right” are related to ethics, the unalert observer may not notice the shift in meaning. Another technique is to spread the shift in meaning out over the course of a lengthy argument. Political speech makers often use phrases such as “equal opportunity,” “gun control,” “national security,” and “environmental protection” in one way at the beginning of a speech and in quite another way at the end. A third technique consists in using such phrases one way in a speech to one group and in a diﬀerent way in a speech to an opposing group. If the same people are not present at both speeches, the equivocation is not detected.

20. Amphiboly

The fallacy of amphiboly occurs when the arguer misinterprets an ambiguous statement and then draws a conclusion based on this faulty interpretation. The original statement is usually asserted by someone other than the arguer, and the ambiguity usually arises from a mistake in grammar or punctuation—a missing comma, a dangling modiﬁer, an ambiguous antecedent of a pronoun, or some other careless arrangement of words. Because of this ambiguity, the statement may be understood in two clearly distinguishable ways. The arguer typically selects the unintended interpretation and proceeds to draw a conclusion based on it. Here are some examples:

The premise of the ﬁrst argument contains a dangling modiﬁer. Is it the observer or the Empire State Building that is supposed to be standing in Greenwich Village? The factually correct interpretation is the former. In the second argument the pronoun “he” has an ambiguous antecedent; it can refer either to John or to Henry. Perhaps John told Henry that Henry had made a mistake. In the third argument the ambiguity concerns what takes place in the biology lecture hall; is it the lecture or the heart failures? The correct interpretation is probably the former. The ambiguity can be eliminated by inserting commas (“Professor Johnson said that he will give a lecture, about heart failure, in the biology lecture hall”) or by moving the ambiguous modiﬁer (“Professor Johnson said that he will give a lecture in the biology lecture hall about heart failure”). Ambiguities of this sort are called syntactical ambiguities.

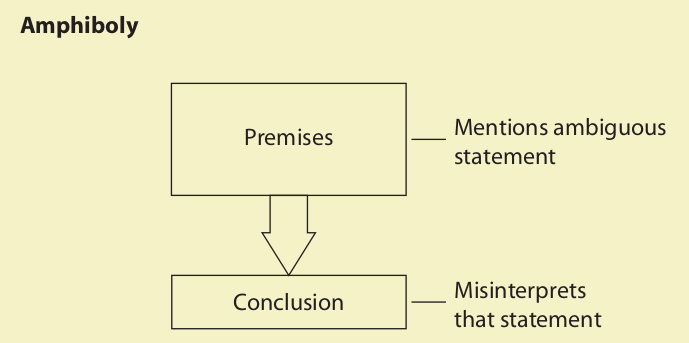
Two areas where cases of amphiboly cause serious problems involve contracts and wills. The drafters of these documents often express their intentions in terms of ambiguous statements, and alternate interpretations of these statements then lead to diﬀerent conclusions. Examples:

In the ﬁrst example the conclusion obviously favors Alice. Theresa is almost certain to argue that the gift of the necklace and chinchilla should be shared equally by her and Alice. Mrs. Hart could have avoided the dispute by adding either “respectively” or “collectively” to the end of the sentence. In the second example, the conclusion favors Mr. James. David will argue that the condition that he ﬁnish by May 1 aﬀected only the Cadillac and that he therefore is entitled to the $5,000. The dispute could have been avoided by properly inserting a comma in the language of the promise.

Amphiboly diﬀers from equivocation in two important ways. First, equivocation is always traced to an ambiguity in the meaning of a word or phrase, whereas amphiboly involves a syntactical ambiguity in a statement. The second diﬀerence is that amphiboly usually involves a mistake made by the arguer in interpreting an ambiguous statement made by someone else, whereas the ambiguity in equivocation is typically the arguer’s own creation. If these distinctions are kept in mind, it is usually easy to dis tinguish amphiboly from equivocation. Occasionally, however, the two fallacies occur together, as the following example illustrates:

First, it is unclear whether “stewed” refers to the oysters or to the diners, and so the argument commits an amphiboly. But if “stewed” refers to the oysters it means “cooked,” and if it refers to the diners it means “intoxicated.” Thus, the argument also involves an equivocation.

21. Composition

The fallacy of composition is committed when the conclusion of an argument depends on the erroneous transference of an attribute from the parts of something onto the whole. In other words, the fallacy occurs when it is argued that because the parts have a certain attribute, it follows that the whole has that attribute, too, and the situation is such that the attribute in question cannot be legitimately transferred from parts to whole. Examples:

In these arguments the attributes that are transferred from the parts onto the whole are designated by the words “Maria likes,” “excellent,” “invisible,” and “deadly poison,” respectively. In each case the transference is illegitimate, and so the argument is fallacious.

Not every such transference is illegitimate, however. Consider the following arguments:

In each case an attribute (having mass, being white) is transferred from the parts onto the whole, but these transferences are quite legitimate. Indeed, the fact that the atoms have mass is the very reason why the teacup has mass. The same reasoning extends to the fence. Thus, the acceptability of these arguments is attributable, at least in part, to the legitimate transference of an attribute from parts onto the whole.

These examples illustrate the fact that the fallacy of composition is indeed an informal fallacy. It cannot be discovered by a mere inspection of the form of an argument—that is, by the mere observation that an attribute is being transferred from parts onto the whole. In addition, detecting this fallacy requires a general knowledge of the situation and of the nature of the attribute being transferred. The critic must be certain that, given the situation, the transference of this particular attribute is not allowed.

Further caution is required by the fact that composition is sometimes confused with hasty generalization. The only time this confusion is possible is when the “whole” is a class (such as the class of people in a city or the class of trees in a forest), and the “parts” are the members of the class. In such a case composition proceeds from the members of the class to the class itself. Hasty generalization, on the other hand, proceeds from the speciﬁc to the general. Because it is sometimes easy to mistake a statement about a class for a general statement, composition can be mistaken for hasty generalization. Such a mistake can be avoided if one is careful to keep in mind the distinction between these two kinds of statements. This distinction falls back on the diﬀerence between the collective and the distributive predication of an attribute. Consider the following statements:

The ﬁrst statement is a general statement. The attribute of being small is predicated distributively; that is, it is assigned (or distributed) to each and every ﬂea in the class. Each and every ﬂea in the class is said to be small. The second statement, on the other hand, is a statement about a class as a whole, or what we will call a “class statement.” The attribute of being numerous is predicated collectively; in other words, it is assigned not to the individual ﬂeas but to the class of ﬂeas. The meaning of the statement is not that each and every ﬂea is numerous but that the class of ﬂeas is large.

To distinguish composition from hasty generalization, therefore, the following procedure should be followed. Examine the conclusion of the argument. If the conclusion is a general statement—that is, a statement in which an attribute is predicated distributively to each and every member of a class—the fallacy committed is hasty generalization. But if the conclusion is a class statement—that is, a statement in which an attribute is predicated collectively to a class as a whole—the fallacy is composition. Example:

At ﬁrst sight this argument might appear to proceed from the speciﬁc to the general and, consequently, to commit a hasty generalization. But in fact the conclusion is not a general statement at all but a class statement. The conclusion states that the whole class of cars uses less fuel than does the whole class of ﬁre trucks (which is false, because there are many more cars than fire trucks). Since the attribute of using less fuel is predicated collectively, the fallacy committed is composition.

22. Division

The fallacy of division is the exact reverse of composition. As composition goes from parts to whole, division goes from whole to parts. The fallacy is committed when the conclusion of an argument depends on the erroneous transference of an attribute from a whole (or a class) onto its parts (or members). Examples:

In each case the attribute, designated respectively by the terms “nonpoisonous,” “made in Seattle,” and “over 300 years old,” is illegitimately transferred from the whole or class onto the parts or members. As with the fallacy of composition, however, this kind of transference is not always illegitimate. The following arguments contain no fallacy:

Obviously, one must be acquainted with the situation and the nature of the attribute being transferred to decide whether the fallacy of division is actually committed.

Just as composition can sometimes be confused with hasty generalization (converse accident), division can sometimes be confused with accident. As with composition, this confusion can occur only when the “whole” is a class. In such a case, division proceeds from the class to the members, whereas accident proceeds from the general to the speciﬁc. Thus, if a class statement is mistaken for a general statement, division may be mistaken for accident. To avoid such a mistake, one should analyze the premises of the argument. If the premises contain a general statement, the fallacy committed is accident; but if they contain a class statement, the fallacy is division. Example:

This example also illustrates how cases of division that involve class statements can include a subtle form of equivocation. In the conclusion, the word “disappeared” means fading from vision, as when the lights are turned down; but in the ﬁrst premise it means rarely seen. The equivocation is a kind of secondary fallacy that results from the primary fallacy, which is division.

The next example shows how division turns up in arguments dealing with averages.

The statement “The average American family has 2.5 children” is not a general statement, but rather a class statement. The sense of the statement is not that each and every family has 2.5 children, but that the class of families is reducible to about 55 percent children and 45 percent adults. Thus, once again, the fallacy is division, and not accident.

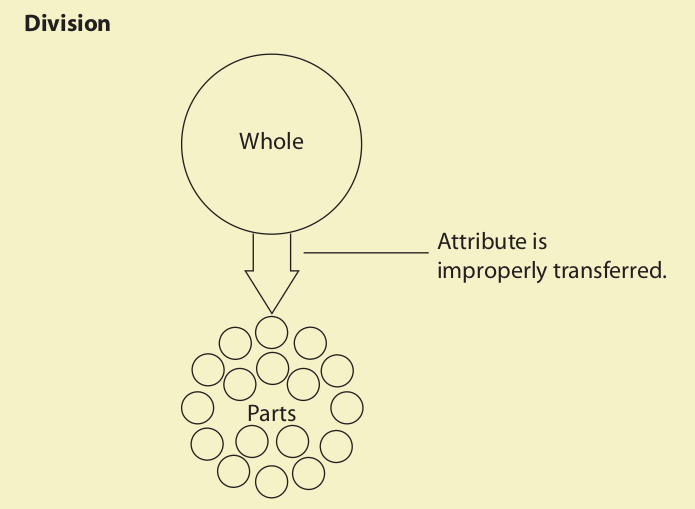
posted on 2025-06-05 14:06 ZhangZhihuiAAA 阅读(27) 评论(0) 收藏举报

刷新页面返回顶部


博客园 © 2004-2025 浙公网安备 33010602011771号浙ICP备2021040463号-3

导航